安庆铁路长江大桥基准动力有限元模型研究

韩州斌, 万华平, 王 乐, 任伟新

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

安庆铁路长江大桥基准动力有限元模型研究

韩州斌, 万华平, 王 乐, 任伟新

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章探讨了大跨度斜拉桥建模中的几个关键问题,即初始平衡构型、斜拉索垂度效应、恒载几何非线性和正交异性桥面板简化,为安庆铁路长江大桥的基准动力有限元模型的建立提供指导;介绍了该桥的现场环境振动试验以及峰值法和随机子空间法的模态参数识别结果。安庆铁路长江大桥有限元模型动力特性的计算结果与实测结果吻合很好,表明建立的有限元模型可作为该桥的基准动力有限元模型。

斜拉桥;基准有限元模型;环境振动试验;峰值法;随机子空间法

有限元模型是基于模型研究工作的基础,例如,抗震抗风设计、模型修正与确认、结构损伤识别及健康监测等,都需要一个精确的有限元模型[1-3]。初始模型因常包含理想化假定及简化而很难反映结构的真实状态,因此有必要对初始模型进行验证和修正。准确的有限元模拟策略和实测数据验证相结合的方法成为建立大型桥梁的基准有限元模型的有效手段[4-6]。

有限元建模策略会影响有限元模型的精度,因此需要选择适当建模策略。斜拉桥的有限元模型主要有单主梁模型[7]、双主梁模型[8]、三主梁模型[9]和空间整体模型[10-11]。文献[12]对一斜拉人行桥分别建立了简化的“脊梁骨”模型和空间整体模型,指出相比于空间整体模型,“脊梁骨”模型存在局限性,未能很好地反映结构的真实状态。文献[13]采用空间整体建模策略对青洲斜拉桥进行有限元模拟,建立的有限元模型可以很好地模拟青洲斜拉桥的静动力行为。本文采用空间整体模型的建模策略对安庆铁路长江大桥进行建模,采用实测数据验证所建的有限元模型的准确性,建立了该桥的基准动力有限元模型。

1 桥梁简介与初始有限元模型

1.1 桥梁简介

安庆铁路长江大桥是南京至安庆城际铁路和阜阳至景德镇铁路的重要组成部分,位于安庆前江口汇合口处下游官山咀附近。该桥主桥为双塔三索面的斜拉桥,全长1 363 m,跨径布置为101.5 m+188.5 m+580.0 m+217.5 m+159.5 m+116.0 m。主梁为三片主桁钢桁梁,桁间距2×14 m,节间长14.5 m,桁高15.0 m。主塔为倒“Y”字形钢筋混凝土结构,塔顶高程+204.00 m,塔底高程-6.00 m,斜拉索为空间三索面,立面上每塔两侧共18对索,全桥216根斜拉索。

安庆铁路长江大桥的总体布置如图1所示。

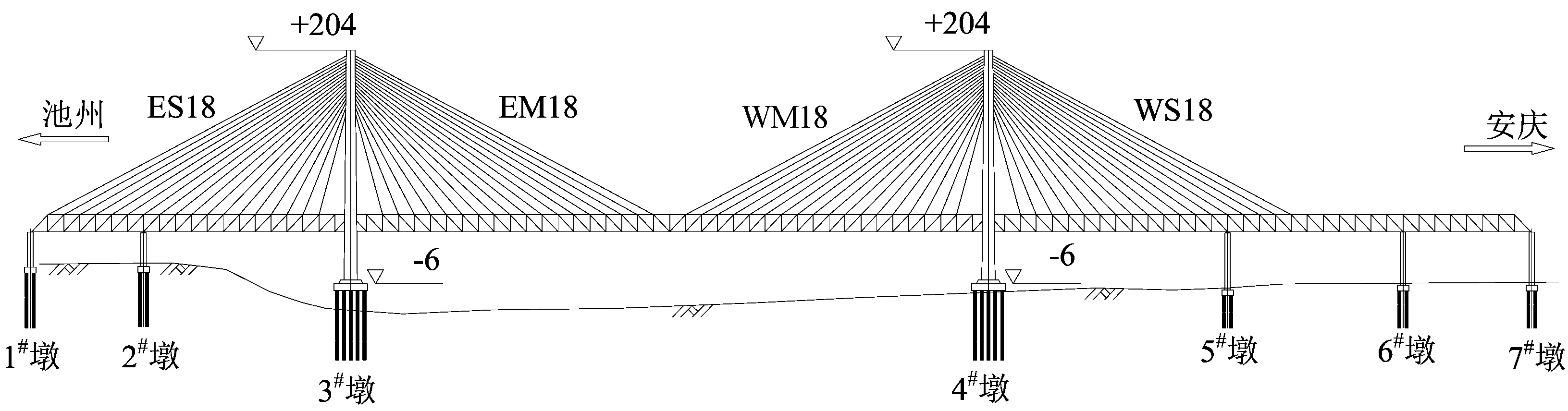
图1 安庆铁路长江大桥总体布置

1.2 初始有限元模型

结构的刚度、质量和边界条件是影响结构动力特性的重要因素,为了建立该桥高精度的动力有限元模型,有必要对这3个主要因素进行细致而准确的模拟。依据实际结构,对不同构件采用相应单元类型来模拟,建立该桥的初始有限元模型如图2所示。

图2 安庆铁路长江大桥有限元模型

(1) 结构有限元模拟。钢桁架上弦杆、下弦杆、竖直腹杆、斜腹杆、横向和竖向连接构件、U肋和倒T型纵梁均采用等截面梁单元(BEAM4)模拟;主塔为变截面,采用变截面梁单元(BEAM188)模拟;斜拉索采用只受拉不受压的杆单元(LINK10)模拟;顶板和横梁采用壳单元(SHELL63)模拟;道砟、道砟槽混凝土板、压重质量、护栏、锚头等非结构构件均采用集中质量单元(MASS21)模拟。

(2) 边界条件模拟。采用耦合相应自由度和约束相应自由度位移的方式来模拟3#塔和4#塔处的边界条件;采用约束相应自由度位移来模拟1#、2#、5#、6#和7#墩处的边界条件。

2 环境振动试验与模态参数识别

2.1 环境振动试验

在大桥正式通车前,于2014年6月对全桥进行了环境激励振动试验。全桥共布置102个测点和2个参考点。全桥模态测试采用分组测试,计11组,前10组每组10个测点，第11组2个测点。测点布置如图3所示。

图3 全桥测点布置

2.2 模态参数识别

采用峰值法(peak-picking, PP)和随机子空间法(stochastic subspace identification, SSI)分别对该桥的模态参数进行识别,峰值法的平均正则化功率谱图和随机子空间法的稳定图如图4所示。5号测站的振动响应识别结果见表1所列。

图4 峰值法的平均正则化功率谱图与随机子空间法的稳定图对比

阶次峰值法f/Hz随机子空间法f/Hz阻尼比/%阵型特征10．26370．26141．20一阶侧弯20．38090．38030．80一阶竖弯30．59570．59420．95二阶竖弯40．75200．74931．93二阶侧弯50．98630．98651．50一阶扭转60．92770．92981．06三阶竖弯71．08391．08403．65四阶竖弯81．41641．41600．60二阶扭转

从图4和表1可以看出,峰值法和随机子空间法的模态参数识别结果吻合良好,表明本文方法能够成功识别出安庆铁路长江大桥的模态参数。考虑到随机子空间法非常适合输入未知结构的模态参数识别,因此随机子空间法的模态参数识别结果可以用来验证该桥的动力有限元模型的准确性。

3 有限元建模中的关键问题

3.1 初始平衡构型

对大跨径斜拉桥,常将恒载和成桥索力共同作用下斜拉桥的平衡位置作为初始平衡构型,该初始平衡位置是结构分析的基准位置。考虑到静力测试结果通常比动力测试结果精确,因此采用以线形为主要目标、索力为次要目标的方法来确定初始平衡构型。有限元模型计算结果与实测结果如图5、图6所示。

图5 桥面线形有限元模型计算值与实测值对比

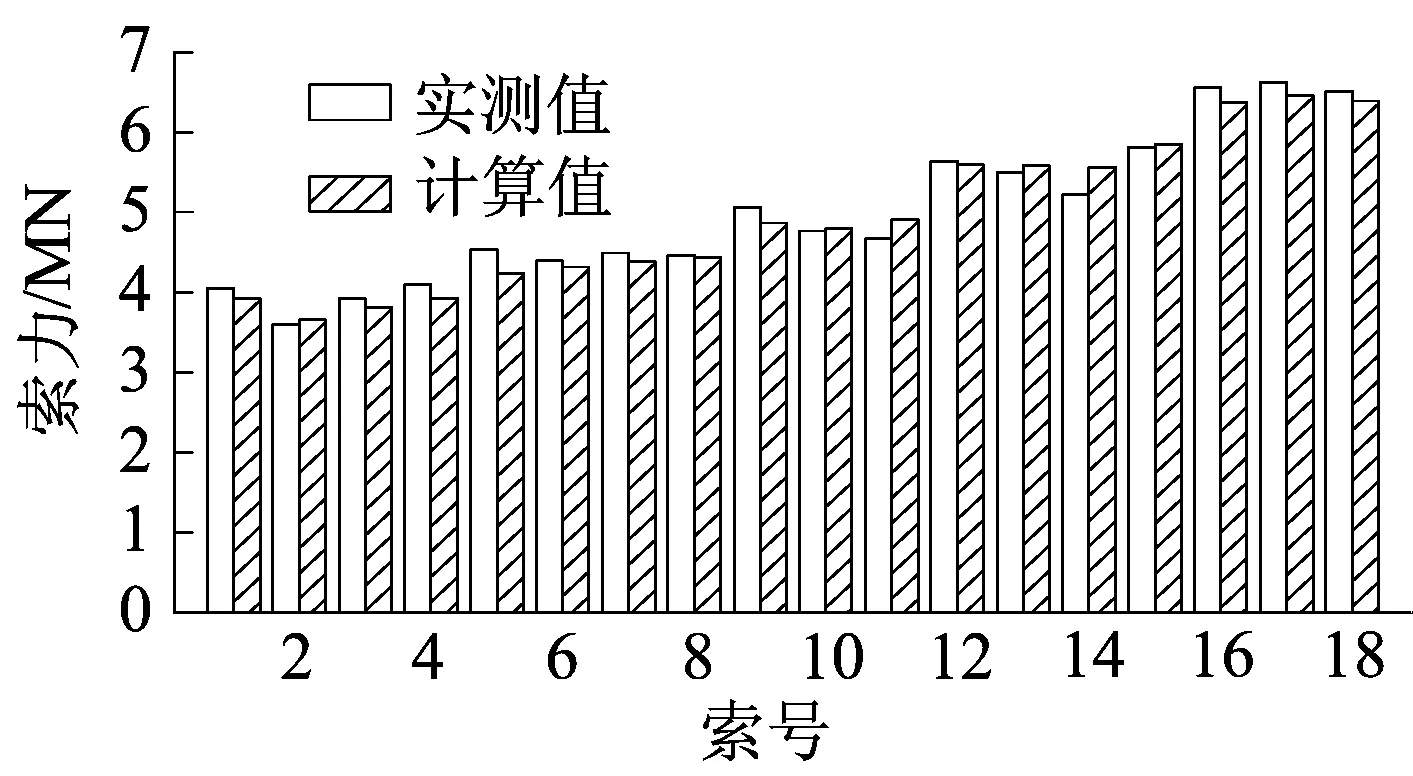
图6 部分边桁索力计算值与实测值对比

首先将设计恒载索力换算成初应变施加到拉索单元上进行静力计算,得到初始桥面线形;然后适当调整索力和二期恒载集度,反复调整校核直至模型的计算线形与实测线形吻合。

由图5、图6可以看出，计算线形和索力与实测线形和索力吻合很好,表明有限元模型满足初始平衡构型要求。

3.2 斜拉索的垂度效应

全桥共216根斜拉索,总质量4 023.9 t,最长索长为301.8 m。考虑到斜拉索的数量多、质量大、长度长,斜拉索的垂度效应对结构的影响不应忽略。本文根据Ernst 公式,采用修正斜拉索弹性模量的方法来考虑斜拉索垂度效应。考虑垂度效应和未考虑垂度效应的模型计算结果见表2所列。

从表2可以看出，斜拉索垂度效应对结构的动力特性和静力特性均有影响,尤其是静力特性,因此基准有限元模型的建立应考虑斜拉索的垂度效应。

表2 斜拉索垂度效应对结构的影响

3.3 正交异性钢桥面板的简化模拟

安庆铁路长江大桥采用正交异性板道砟整体桥面板,由顶板、U肋、T型横梁以及铁轨下的倒T型纵梁组成。本文对正交异性钢桥面板进行简化模拟，依据以下3个原则:

(1) 简化后的质量分布应与原结构等效。

(2) U肋和倒T型纵梁的横向和竖向抗弯刚度均与原结构等效。

(3) 等效后的模型整体抗扭刚度与原结构等效。

为保持正交异性桥面板的空间构造特性,仅简化U肋和倒T型纵梁;采用壳单元模拟顶板和T型横梁,采用梁单元模拟U肋和倒T型纵梁。

3.4 恒载几何非线性

斜拉桥是一种以斜拉索为主要承重构件的柔性体系,随着跨径的增加,几何非线性的影响将更加显著,主要体现在斜拉索的垂度效应、大位移效应和弯矩与轴力的相互作用效应,因此,有必要考虑大跨度斜拉桥的几何非线性对结构静动力特性的影响。

恒载和索力共同作用下,大挠度和小挠度计算结果见表3所列。由表3可以看出，在2种工况下静力和动力计算结果差别较小,在进行大跨度斜拉桥静动力分析时可以不考虑大挠度效应,小挠度计算结果可以满足要求,这与文献[8,13]的结果一致。

表3 几何非线性对结构静动力特性的影响

4 有限元模型的试验验证

仅依据设计图纸建立的有限元模型往往不能准确地反映桥梁的真实状态,因此有必要验证所建模型的准确性。为了比较实测阵型与有限元计算阵型的相关性,采用模态保证准则进行评定,计算公式为：

(1)

其中，φa、φe分别为有限元计算阵型向量和实测阵型向量。

MAC值越接近于1,表明两者相关性越高,吻合越好。

随机子空间法识别的结果与有限元模型计算结果如图7所示,由图7可以看出实测频率与计算频率接近,实测振型与计算振型匹配良好。因此,所建立的有限元模型可以作为安庆铁路长江大桥的基准动力有限元模型。

图7 实测振型与有限元计算振型对比

5 结 论

(1) 空间整体建模策略和实测数据验证相结合的方法是建立大跨度斜拉桥基准有限元模型的一种行之有效的方法。本文采用峰值法和随机子空间法来识别安庆铁路长江大桥的模态参数,结果表明2种方法能识别出大跨度斜拉桥0～1.5 Hz范围内的主要模态参数。

(2) 采用实测桥面线形为主要目标、实测索力为次要目标相结合的方法可以很好地确定斜拉桥的初始平衡构型;小变形可以满足静力分析的要求,但不能忽略斜拉索的垂度效应;采用保留正交异性桥面板整体空间构型,仅简化U肋和倒T型纵梁的方法取得了较好的结果,可为正交异性桥面板的简化模拟提供参考。

(3) 所建立的安庆铁路长江大桥基准动力有限元模型的计算动力特性与实测结果吻合良好,表明该有限元模型能够准确地模拟桥梁的真实状态。因此,该模型可以为安庆铁路长江大桥各类复杂的动力响应分析、健康监测以及状态评估提供可靠的分析依据。

[1] ABDEL-GHAFFER A M，SCANLAN R H.Ambient vibration studies of Golden Gate Bridge:I.suspended structure [J].Journal of Engineering Mechanics，1985，111(4)：463-482.

[2] JAISHI B，REN W X.Structural finite element model updating using ambient vibration test results [J].Journal of Bridge Engineer，2005，131(4)：617-628.

[3] 胡成，汪莲，周安,等.斜拉桥拱塔大缩尺比模型试验研究[J].合肥工业大学学报(自然科学版)，2015,38(6)：816-821.

[4] 李岩，盛洪飞，黄新艺.大跨径斜拉桥动力分析基准有限元模型研究[J].公路交通科技，2006，23(9)：58-62.

[5] 林贤坤，张令弥，郭勤涛,等.预应力连续箱梁桥的基准动力有限元模型研究[J].振动与冲击，2009，28(11)：38-43.

[6] 宗周红，朱三凡，夏樟华.大跨径连续刚构桥安全性评估的基准有限元模型[J].铁道学报，2011，33(9)：94-101.

[7] WILSON J C，GRAVELLE W.Modeling of a cable-stayed bridge for dynamic analysis[J].Earthquake Engineering & Structural Dynamics，1991，20(8)：707-722.

[8] NAZMY A S，ABDEL-GHAFFER A M.Nonlinear earthquake response analysis of long-span cable-stayed bridges：applications[J].Earthquake Engineering & Structural Dynamics，1990，19(1)：63-76.

[9] ZHU L D，XIANG H F，XU Y L.Triple-girder model for modal analysis of cable-stayed bridges with warping effect [J].Engineering Structures，2000，22(10):1313-1323.

[10] 方志，张国刚，唐盛华,等.混凝土斜拉桥动力有限元建模与模型修正[J].中国公路学报，2013，26(3)：77-85.

[11] 丁幼亮，李爱群，缪长青.面向结构安全评估的大跨斜拉桥基准有限元模型[J].东南大学学报(自然科学版)，2007，37(2)：261-265.

[12] 夏品奇，BROWNJOHN J M W.斜拉桥有限元建模与模型修正[J].振动工程学报，2003，16(2)：219-223.

[13] REN W X，PENG X L.Baseline finite element modeling of a large span cable-stayed bridge through field ambient vibration tests [J].Computers and Structures，2005，83(8/9)：536-550.

(责任编辑 张淑艳)

Baseline dynamic finite element modeling of Anqing Railway Yangtze River Bridge

HAN Zhoubin, WAN Huaping, WANG Le, REN Weixin

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

The modeling factors in finite element model of long-span cable-stayed bridge are studied, including the initial equilibrium configuration, cable sag, orthotropic deck simplification and geometrical nonlinearities, aiming at providing guidance for constructing a baseline finite element model of Anqing Railway Yangtze River Bridge. The field ambient vibration tests as well as modal identification of peak picking method and stochastic subspace identification method are presented. The excellent agreement between modal identification results and finite element model derived results is obtained, which demonstrates that the constructed finite element model can be the baseline dynamic finite element model of Anqing Railway Yangtze River Bridge.

cable-stayed bridge; baseline finite element model; ambient vibration test; peak picking method; stochastic subspace identification method

2015-09-28；

2016-11-30

国家自然科学基金资助项目(51508144);中央高校基本科研业务费专项资金资助项目(JZ2015HGBZ0098;JZ2015HGQC0215)

韩州斌(1991-),男,甘肃天水人,合肥工业大学硕士生; 任伟新(1960-),男,湖南长沙人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.01.017

U441.3

A

1003-5060(2017)01-0089-06