智能建筑中空调系统的节能控制设计

张红岭 洪 斌 范竟往

(1.河北建筑工程学院，河北 张家口 075000；2.航天恒星科技有限公司，北京 010000)

0 引 言

智能建筑是一种具有智能的建筑.空调系统耗尽大部分能量，因此有必要采取控制方法得到最优节能通过最好的资源的智能建筑.

空调系统是一个具有复杂特性的系统，比如：多因素，非线性，延迟性，强惯性等.由于很难找出精确的数学模型，所以经典控制理论的功能很难令人满意.由于智能建筑的优势，比如测量、记录和分析数据，一些先进的方法可以用来实现良好的控制效果和理想效率.

1 控制冷却准备时期

建筑在使用之前，空调应该在开始工作时间之前打开，以便能使内部环境达到满意的温度.我们把这段时间称为冷却准备时间.如果时间过长，一些能源将不可避免地损失了；如果时间过短，就不能满足温度要求，如图1所示的开始部分.由于空气温度系统的延迟和不同的初始温度，以及一些其他因素，准备时间很难预测.

在本文中，在智能建筑中，空调系统的冷却准备时间的预测控制通过网络来实现.BP网络具有较强的适应能力和自主性，它适合那些非线性或不确定的控制系统.算法可以接近任何非线性映射关系，而且具有较强的推导能力.因此，它适合于冷却准备预测控制.准备时间Top主要是由室外温度x1，最初的室内温度x2，房间的体积x3和空调的功率x4.

(1)

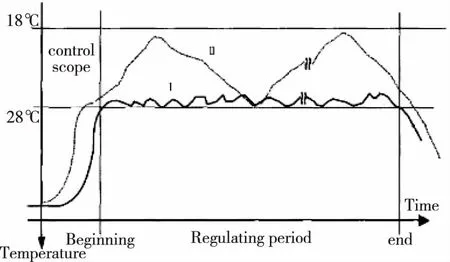
图1 空调系统的节能控制

对于一个给定的建筑物，x3和x4是常数，所以只有x1和x2是需要测量的.这个对象是一个典型的MISO非线性系统.宝贵的数学模型几乎可以通过传统的方式得到.

然而，它可以通过一个改进的BP算法来实现.该网络是由3层组成，分别是输入层、隐藏层和输出层.输入层的节点数n1是2，输出层的节点数n3是1.隐藏层的节点数n2是7，n2是由经验方程计算：

(2)

因为BP算法具有收敛速度慢的缺点，因此，就引入一个修正变量：

ω(k+1)=ω(k)+a(k)·D(k)

(3)

a(k)=2λ·a(k-1)

(4)

λ=sgn[D(k)·D(k-1)]

(5)

D(k)=-∂E(k)/∂ω(k)

(6)

式中，ω是权重；a是研究步骤；D是每级的次数；E是误差，被定义为输入x和输出样本d的函数：

(7)

2 调节时间的前馈控制

空调控制调节时间的主要目标是温度.舒适的温度范围是18-28度，而且建筑物的温度应该保持在里面.通过空调所损耗的能量大约与温度偏差成比例：

(8)

式中，T0是初始温度，T(t)内部温度，TAV是平均温度.

根据统计数据，与25度相比，在夏季，如果内部平均温度保持在20度，电力能源可以节省约35%.所以，如果充分利用建筑物的智能监控，比如各种各样的传感器和控制器，可以调节温度低于上限，从而达到理想的能源效率.如图1的中间部分所示，曲线I比曲线II具有更高的控制分辨率和温度，所以曲线I可以节省更多的能量.

反馈控制只能减少误差.然而，由于空调系统的时间的滞后和控制的延迟，温度曲线就会上下波动正如曲线II一样.因此，本文中提出一种通过前馈控制的节能方法，其主要思想是预先确定控制动作的前置时间以减少控制温度的超调量和波动.

前馈控制和反馈控制不同.它根据干扰来做决定.当系统的扰动发生时，根据它前置控制输出控制值，而且最后删除它.如果算法和参数是正确的，系统就可以轻易得到高控制分辨率和小波动，如图3所示.通过闸门管理系统和能量统计系统，它可以使一个智能建筑“知道”热的变化趋势，就像个人一样.在实际系统中，反馈控制和前馈控制都是用来获得高质量中央空调系统的温度调节.

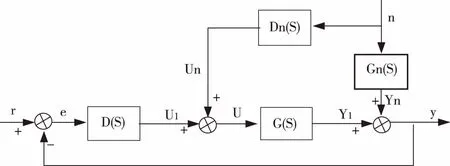
图3 前馈控制系统

如果扰动N(s)是可以测量的，所以由扰动引起的误差Yn(s)将通过前馈环Dn(s)来消除.

Dn(s)G(s)+Gn(s)=0

(9)

所以，前馈控制单元为：

(10)

如果前馈控制和后馈控制都被使用上，控制器可以消除波动，此波动是由可测干扰所造成，并且能减少无法计量的干扰，而且，反馈也具有检测控制结果的功能.前馈和后馈控制器可以大大提高控制解决方案，并获得满意的控制效果和能源效率.采用MATLAB数字仿真系统来实现变风量空调系统的控制的测试.如图4所示，曲线2具有准确的前馈功能，没有误差；曲线3的前馈功能是不准确的，存在扰动，有一些小误差；曲线1只具有反馈功能，有较大的误差.

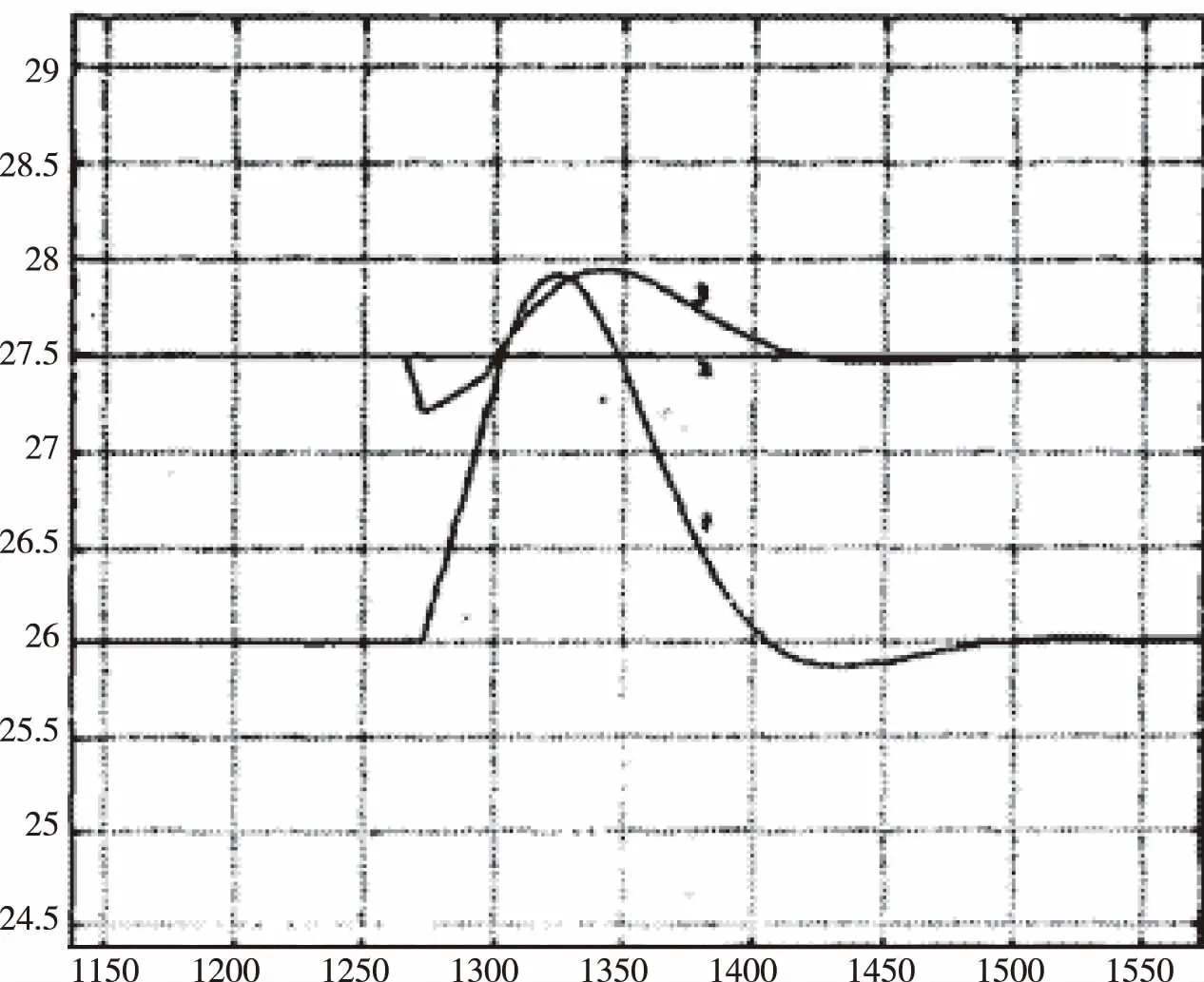
图4 仿真结果

3 开关时间补偿函数

空调停止后，因为系统的特性，内部的温度不会迅速变化.这是系统中的一种惯性.如果利用这个因素，在停止工作的时间之前来完成空调的控制，将不会引起温度的不满足.在空调系统中，这是另一个重要的节能测量，如图1的结束部分所示.先前的开关时间是由许多因素决定的，比如空调的电源，办公设施和人员的热量流失，建筑的体积，当前温度等，以及一些不确定的因素，所以很难预测.

之前的关闭时间早于结束时间，所以有必要保持理想温度.因为有许多随机扰动发生在结束时间之前，比如关闭许多办公设施和增加员工的运动，所以准确的之前关闭时间的函数是不可能实现以便处理这样一个复杂的非线性系统.为了减少困难，这里使用补偿函数，如下所示,

(11)

式中，Top是预测先前的关掉时间；P(i-1)是一个补偿函数；i-1意味着昨天的参数；Ej表示最强的四个因素，分别是在前30分钟的电力消费，建筑物中员工的平均数量，建筑的内部和外部平均温度；k表示他们的体重.对于大多数运行稳定的智能建筑,第一和第二因素可以视为常数k0，尽管有一些偏差.因此，式(11)可以简化如下，

(12)

式中，k0，k1，k2可以通过历史数据的回归计算.

补偿函数P(x)是一个用于非线性优化问题的方法，它把有限的极值问题转化为无限的极值问题.把极小函数P(x)作为上面提到的条件，所以其定义方程应该是：

(13)

式中，M是补偿因子，它代表前几天的预期偏差值，f(x)是求极值的目标函数，该极值满足以下条件,

gi(x)≥0,i=1,2,……，m

(14)

引入一个正函数：

(15)

当限制条件不能满足时，式(15)是正的，所以P(x)将随M增加.因此，看起来像一个补偿(当不满足条件时).当限制条件可以满足时，式(15)是0，因此P(x)就等于f(x)，无论M多大.看起来像没有补偿(当满足条件时).

它是很容易把上面提到的方法付诸到实践中.在预测前关闭空调系统，其条件是：有足够的数据可用，它可以实现良好的控制效果以及良好的能量效率.补偿因子M，它代表了往日的误差，它将函数作为一个校正者来预测今日的误差.因此，预测值将更接近每日的最优值.

[1]M.C.Jean.Scjenf$c Busis of Air Conditioning,London:Applied Science Publisher,1981,pp.15～103

[2]M.Aucevic.“Energy Efficient Office Building Design”,ASHRAE Journal,vol.39.July,1996,pp.26～28

[3]Liu Zuojun.The Control of AC System in Intelligent Building.Master Paper,Hebei University of Technology,Tianjin:PR China,2000,pp.12～35

[4]张芳娥.改进的遗传算法在控制系统参数优化中的应用[J].仪器仪表学报.2003,24(4):605～606

[5]梁春生.中央空调变流量控制节能技术[M].北京:电子工业出版,2005

[6]扈宏杰.基于神经网络自适应稳定控制方法的研究[J].北京航空航天大学学报,2001,4920:153～156

[7]刘战国智能控制在建筑空调控制系统及电梯群控系统中的应用研究[D].重庆大学,2008,10