汽车线控转向系统的模糊滑模控制研究
孔慧芳, 朱 翔, 王 海
(合肥工业大学电气与自动化工程学院,安徽 合肥 230009)
汽车线控转向系统的模糊滑模控制研究
孔慧芳, 朱 翔, 王 海
(合肥工业大学电气与自动化工程学院,安徽 合肥 230009)
针对汽车线控转向系统结构复杂、模型参数具有不确定性以及存在多种干扰源的问题,设计了一种模糊滑模控制方法。基于滑模控制算法,设计了标称控制器和滑模补偿控制器。通过滑模补偿控制器,消除了系统参数的不确定性和路面条件变化对转向性能的影响。采用模糊逻辑设计滑模边界层,削弱了滑模控制中的抖振问题。仿真结果表明,当路面条件发生变化时,模糊滑模控制能有效削弱滑模控制的抖振现象,具有较好的响应速度和鲁棒性。
汽车线控转向系统; 标称控制器; 滑模补偿器; 传感器; 滑模控制; 模糊控制; 鲁棒性; 参数扰动
0 引言
汽车线控转向(steer-by-wire,SbW)系统是近年来国内外研究学者关注的一种新型转向系统,SbW系统去除了方向盘和转向轮之间的机械连接,具有提高汽车安全性、操纵稳定性、驾驶舒适性的特点[1]。目前,SbW系统的控制研究得到了一定的发展和应用。文献[2]提出一种基于分数阶微积分理论的控制器,能够很好地提高转向系统的鲁棒性,但是控制器参数的整定需要不断调试。文献[3]采用滑模控制器跟踪理想车辆模型的质心偏侧角和横摆角速度,但未考虑滑模抖振问题。文献[4]、文献[5]采用饱和函数代替符号函数的方法,对滑模面设置边界层,抑制了抖振问题。但边界层的设置来源于经验,过大或过小的边界层都会影响控制效果。
本文在前人研究成果的基础上,设计了模糊滑模的控制方法,将滑模面和滑模面的导数作为模糊控制器的输入。这种设计方法可以自适应地调整边界层的厚度,消除系统抖振。仿真分析中给出了沥青路面和雨雪路面两种路面情况下的仿真结果。结果表明,该控制方法具有良好的响应速度和鲁棒性,能够满足线控转向系统的跟随性能要求。
1 线控转向系统建模
SbW系统结构示意图如图1所示。
SbW系统可分为转向盘模块、控制器和转向前轮模块3个部分。转向盘模块包含转向盘、路感电机、转向盘角传感器;转向前轮模块包含转向执行电机、转向前轮、齿轮角传感器等部件。转动转向盘时,会产生一个转角参考信号,控制器根据转向盘模块给出的转角参考信号和车速信号,发出控制命令到转向电机,使得转向前轮跟随转角参考信号。

图1 SbW系统结构示意图
1.1 转向盘总成模型
方向盘模型为:
(1)
路感电机模型为:
(2)
采用直流电机,电机电路方程为:
(3)
电机电磁转矩为:
Tm1=Kmim
(4)
以上公式中:Tsw为驾驶员施加到转向盘上的力矩;Jsw为转向盘转动惯量;Bsw为转向柱阻尼系数;θh为转向盘转角;Ksw为转向柱的扭转刚度;θm1为路感电机转角;gm1为减速比;Tm1为路感电机电磁力矩;Jm1为路感电机转动惯量;Bm1为路感电机阻尼系数;Rm为电枢电阻;im为电机电流;Um为电机电压;Lm为电机电感;Km为电机转矩系数。
1.2 转向前轮总成模型
转向执行电机模型为:
(5)
转向前轮模型为:
(6)
式(5)、式(6)中:Jm2为执行电机转动惯量;Bm2为执行电机阻尼系数;Tm2为执行电机电磁扭矩;θm2为执行电机转角;Tr为执行电机经减速机构后对外输出的扭矩;ηm2为减速机构的效率;gm2为减速机构减速比;Tf为系统摩擦扭矩;Te为正力矩作用在齿条上的扭矩;Jw为前轮的转动惯量;Bw为前轮的阻尼系数;Tz为转向电机施加到前轮的力矩;θf为转向前轮转角。
(7)
(8)
式中:c1为前轮侧偏刚度系数;a为质心到前轮距离;v为车速;c2为后轮侧偏刚度系数;b为质心到后轮距离;m为整车质量;Iz为车辆转动惯量。
假设齿轮与齿条之间没有间隙,可以得到θm2和它们各阶导数之间的关系如下:
(9)
式中:K为传动比。
1.3 系统模型
结合式(5)、式(6)以及式(9),得到的转向前轮模块等效模型如下:
(10)
式中:Jeq和Beq为等效的转动惯量和阻尼系数。
Jeq=Jw+K2Jm2
(11)
Beq=Bw+K2Bm2
(12)
u=KTm2
(13)
考虑系统的标称值和不确定部分影响,式(10)改写如下:
(14)
式中:d为系统总的不确定部分。
d可表示为:
(15)
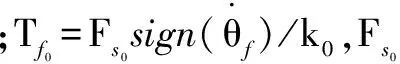
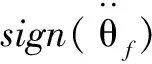
(16)
2 控制器设计
2.1 滑模控制器设计
转向前轮参考转角为:
(17)
式中:θhr(t)为转向盘参考角;θh(t)为转向盘轴转角;N为转向盘模块传动比。
定义跟随误差e(t)为:
e(t)=θf(t)-θhr(t)
(18)
(19)
由式(19)可以得到系统跟随误差的二阶导数如下:

(20)
(21)
式中:d′为等效系统总的不确定部分。
将u(t)分为标称控制和滑模补偿控制两部分:
u(t)=u1(t)+u0(t)
(22)
式中:u1(t)为标称反馈控制器(nominal feedback controller,NFC);u0(t)为系统滑模补偿控制器(sliding mode compensator,SMC)。

(23)
式中:k1、k2满足Hurwitz多项式条件。

(24)
根据滑模控制的基本思想,选择线性切换函数,定义滑模变量:
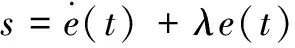
(25)
式中:λ为大于0的正数。
为了使跟随误差e渐近收敛到0,设计滑模补偿控制器为:
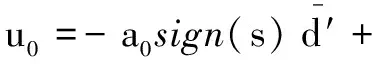

(26)

考虑Lyapunov函数V=s2/2,可以证明得到:
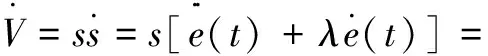

(27)

不等式(27)确保了滑模变量最终能够到达滑模面。
滑模补偿控制器u0是为了补偿系统的不确定性、非线性等因素而加入的不连续控制部分,它的存在提高了系统的鲁棒性,但同时也引起了系统状态环绕滑模面的抖振。
去除抖振的一个有效方法是在滑模面附近引入一个边界层,将滑模控制不连续部分的符号函数修改为饱和函数[4-5]:

(28)
式中:σ为边界层的宽度。
2.2 模糊滑模控制器设计
在滑模控制中,虽然引入了边界层控制方法削弱抖振,但是过窄的边界层,对不确定系统的高频抖振消除效果不明显;过宽的边界层,又会出现较大的稳态误差[6-7]。边界层的选取往往采用经验和试凑法。若采用固定的边界层,将无法很好地适应系统参数发生变化(比如路面条件变化)对滑模系统抖振的抑制效果。为获得最佳的抖振抑制效果,应用模糊规则对边界层的厚度进行调整。
本文设计模糊逻辑系统的输入量为s,表示任意点到滑动面的相对距离。模糊逻辑系统的输出量为滑模控制边界层的宽度。定义模糊语言变量为7个子集:负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB),并定义输入论域均为{-3,3},输出模论域为{0,1},超过此范围按边界值处理。根据专家经验和试验修正,建立如表1所示的控制规则表。
表1 模糊规则表
Tab.1Fuzzyrules

σsNBNMNSZPSPMPBNBNBNBNMNMNSNSZNMNBNMNMNSNSZPSNSNMNMNSNSZPSPSZNMNSNSZPSPSPMPSNSNSZPSPSPMPMPMNSZPSPSPMPMPBPBZPSPSPMPMPBPB
表1中的控制规则可以用以下模糊条件语句来描述:
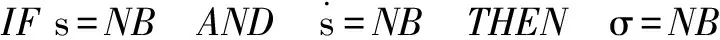
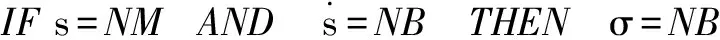

模糊输入量和输出量选取相同的隶属度函数,NB选择Z型隶属度函数,PB选择S型隶属度函数,其余均选择如图2所示的三角形隶属度函数。

图2 隶属度函数示意图
由模糊控制器给出的控制量需要进行清晰化处理,本文采用重心法解模糊[8]。
(29)
3 仿真结果及分析
以某款汽车线控转向系统为例,模糊滑模控制器结构[8-10]如图3所示。

图3 模糊滑模控制器结构图
为了验证所设计模糊滑模控制器的有效性,利用Matlab编写SbW系统的固定边界层滑模控制算法和模糊滑模控制算法。设置两种不同的路面情况,以验证当系统参数改变时模糊滑模控制对系统抖振的抑制效果。
在0s时,给转向盘输入一个正弦信号,汽车车速为60km/h;0~15s时为雨雪路面、15~30s时为沥青路面。仿真得到转向前轮对于给定参考信号的跟随性能和控制器输出扭矩信号。图4为固定边界层滑模控制器仿真曲线。从仿真曲线可以看出,当转向盘输入一个正弦转角信号,固定边界层取0.27时,转向前轮转角在整个仿真过程中能够很好地跟随参考转向信号,最大跟随误差为±0.253rad。由图4(b)可见,当路面情况发生变化时,控制系统具有较大的抖振,且不能逐渐稳定。

图4 固定边界层滑膜控制器仿真曲线
图5为模糊滑模控制器仿真曲线。

图5 模糊滑膜控制器仿真曲线
对系统边界层进行模糊控制后,系统的最大跟随误差为±0.242rad。当路面情况发生变化时,传统滑模控制和模糊滑模控制均表现出很好的鲁棒性。
模糊控制器的滑模边界层输出示意图如图6所示。

图6 模糊控制器的滑模边界层输出示意图
4 结束语
在分析滑模控制原理的基础上,给出了一种模糊滑模控制器的设计方法。将滑模控制器分为标称控制器和滑模补偿器,利用滑模补偿器消除系统不确定性和外界干扰对系统的影响;并将模糊控制方法应用于滑模边界层的自适应调整,从而抑制系统参数发生变化时的系统抖振问题。
最后将模糊滑模控制器应用于某汽车线控转向系统的控制器,并给出仿真结果。结果表明,基于边界层模糊调节的滑模控制方法,根据系统滑模变量状态的变化,动态模糊调整滑模边界层的宽度,有效改善了当环境变化时固定边界层[11-13]滑模控制存在的抖振问题,对系统参数变化具有很强的鲁棒性,非常适合应用在汽车线控转向系统。
[1] 田争芳.基于模糊滑模控制的汽车线控转向系统研究[D].济南:山东理工大学,2013.
[2] 田杰,高翔,陈宁.基于分数阶微积分的线控转向系统的控制研究[J].机械科学与技术,2010,29(9):1172-1176.
[3] 韩坤,任春燕.基于滑模控制的线控转向系统仿真[J].湖北汽车工业学院学报,2013,27(3):1-4.
[4] 彭晓燕.汽车线控制动系统安全控制技术研究[D].长沙:湖南大学,2013.
[5]CAOJB,CAOBG.Fuzzy-logic-basedsliding-modecontrollerdesignforposition-sensorlesselectricvehicle[J].PowerElectronicsIEEETransactionson,2009,24(10):2368 - 2378.
[6]ERBATURK,KAWAMURAA.Chatteringeliminationviafuzzyboundarylayertuning[C]//IECON.IEEE,2002:2131-2136.
[7] 杨玲玲,章云,陈晓龙.一类不确定非线性系统的模糊边界层滑模控制[J].系统仿真学报,2009,21(22):7262-7265.
[8] 李士勇.模糊控制·神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998.
[9]WANGH,MANZ,SHENW,etal.Robustcontrolforsteer-by-wiresystemswithpartiallyknowndynamics[J].IEEETransactionsonIndustrialInformatics,2014,10(4):2003 - 2015.
[10]余志生.汽车理论[M].3版.北京:机械工业出版社,2005.
[11]张晓宇,陈文卓,申斌.一种离散模糊滑模边界层自适应的消抖方法[J].自动化仪表,2015,36(8):1-6.
[12]WANGH,KONGH,MANZ,etal.Slidingmodecontrolforsteer-by-wiresystemswithACmotorsinroadvehicles[J].IEEETransactionsonIndustrialElectronics,2014,61(3):1596 - 1611.
[13]ZHANGX,KONGH,WANGH.Acompositecontrolschemeforautomotivesteer-by-wiresystem[C]//2014Proceedingsofthe6thInternationalConferenceonModelling,Identification&Control(ICMIC).IEEE,2014:237-242.
ResearchontheFuzzySlidingModeControlofAutomobileSteer-by-WireSystem
KONGHuifang,ZHUXiang,WANGHai
(SchoolofElectricalEngineeringandAutomation,HefeiUniversityofTechnology,Hefei230009,China)
Theautomobilesteer-by-wiresystemfeaturescomplexstructures,uncertainmodelparametersandfacingmultipledisturbances,aimingattheseissues,afuzzyslidingmodecontrolschemeisdesigned.Thenominalcontrollerandslidingmodecompensationcontrolleraredesignedbasedonslidingmodecontrolalgorithm,theuncertaintyofthesystemparametersandtheinfluenceofvariationofroadsurfaceconditionsonsteeringperformanceareeliminatedthroughslidingmodecompensationcontroller.Inaddition,theslidingmodeboundarylayerisdesignedbyusingfuzzylogictorelievethebuffetingprobleminslidingmodecontrol.Thesimulationresultsshowthatthefuzzyslidingmodecontrolcaneffectivelyrelievethebuffetingphenomenonwhenconditionsofroadsurfacechange,anditpossessesbetterresponsespeedandstrongrobustness.
Automobilesteer-by-wiresystem;Nominalcontroller;Slidingmodecompensator;Sensor;Slidingmodecontrol;Fuzzycontrol;Robustness;Parameterperturbation
中央高校基本科研业务费专项资金资助项目(2014HGCH0003)
孔慧芳(1964—),女,博士,教授,主要从事新能源汽车电控技术、自动变速箱电控技术的研究。E-mail:konghuifang@163.com。朱翔(通信作者),男,在读硕士研究生,主要研究方向为新能源汽车电控技术。E-mail:www.zhu-xiang@163.com。
TH-3;TP
ADOI: 10686/j.cnki.issn1000-0380.201701007
修改稿收到日期:2016-05-19

