内模补偿预测函数控制在磁悬浮系统中的应用
孟凡斌, 邵雪卷, 张井岗, 陈志梅
(太原科技大学电子信息工程学院,山西 太原 030024)
内模补偿预测函数控制在磁悬浮系统中的应用
孟凡斌, 邵雪卷, 张井岗, 陈志梅
(太原科技大学电子信息工程学院,山西 太原 030024)
由于磁悬浮系统参数时变及外界干扰的存在,采用预测函数控制会产生较大的预测误差,导致系统性能变差。针对这个问题,提出了一种基于内模补偿的预测函数控制方法。采用内模控制器的输出修正预测函数控制(PFC)补偿系统的控制量,克服不确定因素的影响,改善系统的控制品质。仿真和试验结果表明,该方法不仅能使磁浮球装置中的小球快速到达平衡位置,而且提高了系统的抗干扰能力和控制精度。
磁悬浮; 轨道交通; 工业机器人; 预测函数控制; 神经网络控制; 二自由度; 预测误差; 内模补偿; 控制精度
0 引言
磁悬浮是一种利用磁力使物体在空间中处于悬浮平衡状态的支撑技术,具有无接触、无摩擦等优点,可以延长机械设备的使用寿命。近年来,磁悬浮技术在轨道交通运输、非接触式驱动、精密加工、航空航天、生命医学等领域获得了广泛应用[1],具有重要的研究与应用价值。但是,磁悬浮系统是一类非线性不确定系统,具有一定的控制难度,传统PID控制很难满足其对高精度及快速性的要求。近年来,国内外研究者提出了诸多控制方法,如:鲁棒控制[2]、滑模变结构控制[3-4]、模糊控制[5-6]、神经网络控制[7]等。这些方法从不用角度改善了系统的控制品质,但是仍存在控制器设计复杂、算法计算量大等问题。
预测函数控制(predictivefunctioncontrol,PFC)最早由Richalet等提出,一经问世便被成功应用于工业机器人的跟踪控制中[8]。此后,PFC在理论研究和实际应用中均取得了一系列成果。近年来,国内外研究者分别从预测模型[9-10]、基函数[11-13]、目标函数[14-16]等方面对预测函数控制进行了改进,并且将单一变量系统扩展到了多变量系统[17-19]。PFC算法具有计算简单、快速性好、鲁棒性强等特点,目前已被应用于电机控制、轧钢控制、飞行器控制等领域。
PFC结构考虑了系统的模型失配和噪声等问题,但是其调节能力有限。由于参数时变和干扰等因素的存在,PFC的模型输出和实际输出之间会存在较大的预测误差,影响磁悬浮系统的控制性能,甚至会破坏其稳定性。为了减小预测误差,增强系统的抗干扰性能,本文在常规PFC的基础上,采用内模控制器补偿系统的控制量。仿真和试验表明,该方法具有更好的动态性能及控制精度。
1 预测函数控制原理
预测函数控制属于预测控制的范畴,具有预测模型、滚动优化和反馈校正三个基本特征。
1.1 预测模型
预测模型常采用离散状态空间表达式形式:
(1)
式中:Xm(t)为t时刻广义预测模型的状态向量;ym(t)为t时刻模型的预测输出;Am、Bm和Cm为预测模型的系数矩阵。
基函数的线性组合形式如下:
(2)
式中:fkj(i)为基函数的第i个采样周期值;Nf为基函数的个数;μj(k)为基函数的线性组合系数;h为优化时域长度。
1.2 滚动优化
参考轨迹通常采用一阶指数形式,即:
yr(k+i)=βiyp(k)+(1-βi)r(k)
(3)
式中:yr(k+i)为参考轨迹;r(k)为设定值;yp(k)为广义对象的实际输出;参考轨迹柔化因子β=e[-Ts/(Tr/3)],0<β<1。
采用二次型优化目标函数:
(4)
式中:NH为拟合点的数量;hj为第j个拟合点。
定义yp(k+i)为(k+i)时刻的广义对象输出预测,其计算表达式为:
yp(k+i)=ym(k+i)+ε(k+i)
(5)
式中:ym(k+i)为(k+i)时刻的广义预测模型输出;ε(k+i)为(k+i)时刻预测误差。
1.3 反馈校正
由于系统存在不确定因素,会使模型预测输出和实际输出之间存在一定的偏差,PFC需要对未来时域中的误差进行预测,一般选取预测误差为:
ε(k+i)=yp(k)-ym(k)
(6)
式中:yp(k)为k时刻被控对象的实际输出;ym(k)为k时刻预测模型的输出。
2 磁悬浮球系统的PFC控制
2.1 磁悬浮球系统的数学模型
磁浮球装置包括电磁铁、小球、光源、光电位置传感器、功率放大电路等,其结构如图1所示。

图1 磁浮球装置结构图
图1中:m为小球质量;g为重力加速度;x为钢球质心和电磁铁磁极之间的距离;f为电磁力;ui为外部电路设备所提供的电压;ux为小球位置对应的传感器的输出电压。
由文献[1]、文献[3]可知,系统在平衡位置(i0,x0)附近的传递函数为:
(7)
式中:x0为平衡位置;i0为平衡位置处的电流。
实际控制中,以功率放大器的输入电压u作为控制量,此时传感器的输出电压Ux和功率放大器的输入电压Ui之间的关系为:
(8)
式中:b=-2gKx/(Kai0);p2=2g/x0;1/Ka为功率放大器增益;Kx为输出电压的转换系数。
磁悬浮装置物理参数如下[20]:平衡位置x0=0.02m;平衡电流i0=0.610 5A;重力加速度g=9.8m/s2;Ka=5.892 9A/V;Kx=-458.845 6V/m。
将以上这些参数代入式(8),可得系统参数b=2 499.1。
2.2 磁悬浮球系统的整定
由式(8)可以看出,磁浮球系统在复平面的右半平面s内有一个不稳定的极点,s平面是一个不稳定系统。因此,选取比例微分结构进行整定,即:
H(s)=kp+kds
(9)
由式(8)和式(9)可得整定后的广义对象为:
实施儿童肥胖干预的场所有学校、家庭、社区等,在学校实施肥胖干预,便于组织实施和持续进行。由于城市学龄儿童入学率高,在校时间长,使得学校成为预防和干预学龄儿童肥胖的最佳场所。本研究以校园为主要干预环境,同时向家庭发散。采用分级培训式健康教育,探讨培养学龄儿童健康生活方式,降低肥胖发生率的策略,具有重要的社会价值和现实意义。
(10)
典型二阶系统的数学模型:
(11)
对比式(10)和式(11),可得整定后广义被控对象的模型参数为:
(12)
(13)
(14)
式中:ωn为自然频率;ξ为系统的阻尼比,取ξ=0.8。此时,G(s)的所有极点都位于s平面的左平面内,G(s)是一个稳定的典型二阶广义被控对象。
2.3PFC控制器设计
磁悬浮系统的PFC结构如图2所示。

图2 磁悬浮系统的PFC结构图
图2中:P为被控对象;G为整定后的广义被控对象;Gm为预测模型(即Gm=G);r为设定值;d为干扰;yp为系统的实际输出;ym为模型的预测输出。
当给定值为阶跃信号时,选择单位阶跃函数作为基函数,即新加入的控制作用为:
u(k)=μ(k)i=0,1,2,...,h-1
(15)
由式(1)、式(10)~式(14)可知,系统的预测模型系数矩阵为:
(16)
(17)
Cm=[1 0]
(18)
根据PFC原理递推,由∂J(k)/∂u(k)=0,可得k时刻的PFC控制量:
u(k)=K0[r(k)-yp(k)+KmXm(k)]
(19)
式中:K0和Km为增益系数,可通过离线计算求得。
3 内模补偿控制器设计
为了克服外界干扰和参数时变等因素引起的预测误差,在常规PFC基础上设计补偿结构,增强PFC的抗干扰能力,其控制结构如图3所示。

图3 带补偿的PFC结构图
图3中:F为补偿控制器,根据预测误差修正控制量u,使系统输出yp和模型输出ym尽可能相等。
目前,常用的补偿方法有模糊控制[20]、神经网络控制[21]、扰动观测器[22-23]等。
为了使系统获得良好的干扰抑制特性,本文采用内模控制方法进行设计,即:
(20)

f(s)的表达式为:
(21)
根据式(10)~式(12)、式(17)~式(18),可得内模补偿控制器为:
(22)
式中:n=2。
4 系统性能分析
4.1 理论分析
PFC的控制器参数K0和Km可以离线求得。因此,该内模补偿PFC可以等效为如图4所示的结构。

图4 等效的内模补偿PFC结构图
系统的输入、输出关系可表示为:

(23)
标称情况下,目标值输入的传递函数和干扰输入的传递函数分别为:
(24)
(25)
由上式可以看出,该补偿PFC结构实现了目标值跟随性能和干扰抑制性能的解耦。根据二自由度控制思想,PFC控制器和内模控制器的参数可以分开调节,使系统同时获得良好的目标值跟随特性和干扰抑制特性。
根据式(25),可得标称情况下系统的干扰抑制传递函数为:
(26)
对式(25)进行进一步变换,可得:
(27)
由鲁棒控制理论可知,当增大λ时,S(s)增大,系统的干扰抑制特性变差;相反,当减小λ时,系统的干扰抑制特性增强。
4.2 仿真分析
在标称情况下,设定值r=-3V,当t=0.5s时加入幅值为0.6V的阶跃干扰。当λ=0.01,取Tr分别为0.05、0.1、0.15时,系统阶跃响应曲线如图5(a)所示;当Tr=0.1,取λ分别为0.005、0.01、0.015时,系统阶跃响应曲线如图5(b)所示。

图5 参数变化时的系统阶跃响应曲线
由图5(a)可知,当λ不变时,随着Tr的减小,系统的系统响应速度加快,干扰抑制能力增强;相反,随着Tr的增大,系统响应速度减慢,干扰抑制能力减弱。由图5(b)可知,当Tr不变时,减小λ,系统的干扰抑制能力增强;增大λ,系统的干扰抑制能力减弱。可见,Tr影响系统的跟随性能和抗干扰能力,λ的变化只影响抗干扰能力,这与理论分析的结论一致。
此外,在进行控制器参数选择时,先确定Tr,再确定λ,使系统同时获得良好的目标值跟随性能和抗干扰能力。
5 仿真和试验
为了证明本文内模补偿PFC的控制效果,分别进行仿真和试验研究。选择超调量(σ%)、调节时间(ts)、稳态误差(Δ)及时间乘以误差绝对值积分(interatedtimeandabsoluteerror,ITAE)作为验证系统性能的指标,并将本文方法与PID、常规PFC方法进行比较。
5.1 仿真
分别比较标称和模型失配两种情况下系统的控制性能,模型失配时使系统参数p2和b分别摄动-30%,即p2=686、b=1 749.37。两种情况下系统的阶跃响应曲线如图6所示。仿真性能指标比较如表1所示。

图6 系统阶跃响应比较曲线
PID控制器参数:Kp=1.5、KiTs=0.01、Kd/Ts=45,常规PFC参数Tr=0.1,内模补偿PFC参数Tr=0.1、λ=0.01。
由仿真结果可以看出,本文内模补偿PFC方法的动态性能和抗干扰能力均优于常规PFC和PID控制。
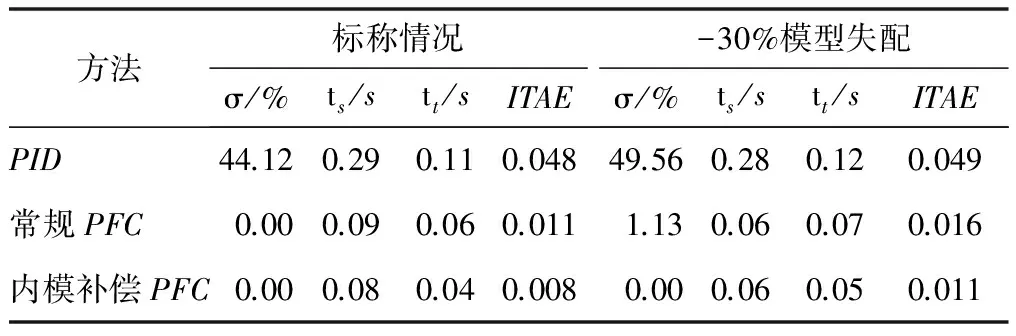
表1 仿真性能指标比较
5.2 试验
本文采用图7所示的磁悬浮球系统试验平台进行试验研究。该平台主要由磁悬浮装置、dSPACEDS1103控制板、工控机等部分组成。

图7 磁悬浮球系统试验平台
由于试验装置的传感器输出电压为负值,因此,给定位置电压为-3V,在15s左右加入干扰。磁悬浮球系统的位置输出曲线如图8所示。控制性能指标比较如表2所示。

图8 系统实时控制输出曲线
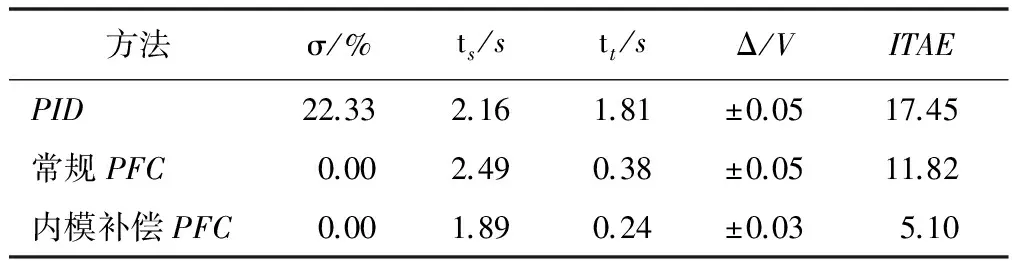
方法σ/%ts/stt/sΔ/VITAEPID22.332.161.81±0.0517.45常规PFC0.002.490.38±0.0511.82内模补偿PFC0.001.890.24±0.035.10
通过试验比较可以看出,内模补偿PFC方法的位置跟踪过程无超调,调节时间最短,仅为1.89s;干扰作用后的调节时间仅为0.24s;稳态误差为0.03V;30s内的ITAE指标为5.10。因此,本文内模补偿PFC方法的动态性能及干扰抑制能力均优于另外两种控制系统,这与仿真结论一致。
6 结束语
本文针对磁悬浮系统的位置控制,设计了一个内模补偿PFC控制器。为了克服不确定因素的影响,采用内模控制器补偿PFC控制量,减小预测误差,提高PFC的抗干扰能力。由于该控制结构中的PFC控制器和内模控制器参数可以分别选择、调节,因此能够同时满足对系统快速性和干扰抑制特性的要求。仿真和试验表明,该控制系统具有快速性好、抗干扰能力强、控制精度高等特点。
[1]GHOSHA,KRISHNANTR,TEJASWYP,etal.Designandimplementationofa2-DOFPIDcompensationformagneticlevitationsystems[J].ISATransactions,2014,53(4):1216-1222.
[2]CHOUDHARYSK.Robustfeedbackcontrolanalysisofmagneticlevitationsystem[J].WseasTransactiononSystems,2014,13(6):285-291.
[3] 张井岗,方线伟,赵志诚.磁悬浮球系统的分数阶滑模控制[J].南京理工大学学报,2014,38(1):72-77.
[4]MEENAN,SHARMABB.Backsteppingalgorithmwithslidingmodecontrolformagneticlevitationsystem[J].InternationalJournalofEmergingTrendsinElectricalandElectronics,2014,10(3):39-43.
[5] 彭辉,徐锦华,侯海良,等.模糊控制在磁悬浮球系统实时控制中的应用[J].控制工程,2009,16(3):278-281.
[6]BENOMAIRAM,TOKHIMO.Controlofsingleaxismagneticlevitationsystemusingfuzzylogiccontrol[J].InternationalJournalofAdvancedComputerScience&Applications,2013,4(11):51-56.
[7] 赵石铁,高宪文,车昌杰.基于RBF神经网络的非线性磁悬浮系统控制[J].东北大学学报(自然科学版),2014,35(12):1673-1676,1696.
[8] 金晓明,王树青,荣冈.先进控制技术及应用第五讲预测函数控制(PFC)——一种测控制策略[J].化工自动化及仪表,1999,26(6):74-80.[9] 陈进东,张相胜,潘丰.基于wiener模型的非线性预测函数控制[J].吉林大学学报(工学版),2011,41(增刊1):264-269.
[10]ZHANGJM.Anon-minimalstatespaceformulationbasedpredictivefunctionalcontroldesignforinverse-responseprocesses[J].Chemometrics&IntelligentLaboratorySystems,2014,139(6):70-75.
[11]侯宁,费树岷,周磊.基于小波函数的预测函数控制方法研究[J].西南大学学报(自然科学版),2014,36(2):136-142.
[12]赵寅军,陈国定,张伯立.阶跃基权系数时变的预测函数控制[J].计算机仿真,2012,29(1):79-82.
[13]ZHANGRD,WUS,GAOFR.ImprovedPIcontrollerbasedonpredictivefunctionalcontrolforliquidlevelregulationinacokefractionationtower[J].JournalofProcessControl,2014,24 (3):125-132.
[14]郭伟,吴东,吴青.基于PID预测函数的励磁控制研究[J].控制工程,2012,19(5):757-760,764.
[15]郭伟,倪家健,李涛,等.基于时域的分数阶PID预测函数励磁控制器[J].仪器仪表学报,2011,32(11):2461-2467.
[16]周磊,费树岷,黄家才.一种新型的预测函数PID控制算法的研究[J].自动化仪表,2013,34(9):63-66.
[17]WUS.StatespacepredictivefunctionalcontroloptimizationbasednewPIDdesignformultivariableprocesses[J].ChemometricsandIntelligentLaboratorySystems,2015,143(5):16-27.
[18]苏成利,施惠元,李平,等.增量式多变量预测函数控制及其在气体分馏装置中的应用[J].南京理工大学学报,2015,39(5):625-631.
[19]张运诗,仲兆准,钟胜奎,等.分布式预测函数控制优化算法[J].自动化仪表,2014,35(7):68-73.
[20]杜建根,唐建生,黄建娜.模糊预测函数控制在倒立摆上的应用研究[J].武汉理工大学学报,2008,30(1):146-149.
[21]朱坚民,沈正强,李孝茄.基于神经网络反馈补偿控制的磁悬浮球位置控制[J].仪器仪表学报,2014,35(5):976-986.
[22]邓永停,李洪文,王建立,等.基于预测函数控制和扰动观测器的永磁同步电机速度控制[J].光学精密工程,2014,22(6):1598-1605.
[23]尹成强,岳继光.非自衡时滞对象的改进内模控制[J].控制与决策,2009,24(10):1593-1596,1600.
PredictiveFunctionalControlBasedonInternalModelControlCompensatingforMagneticLevitationBallSystem
MENGFanbin,SHAOXuejuan,ZHANGJinggang,CHENZhimei
(CollegeofElectronicInformationEngineering,TaiyuanUniversityofScienceandTechnology,Taiyuan030024,China)
Thetimevaryingparameterofthemagneticlevitationballsystemandthedisturbanceintheworkingenvironmentresultinalargepredictionerrorofthepredictivefunctionalcontrol,whichwillmakethesystemperformanceworse.Tosolvethepredictionerrorproblem,aninternalmodelcontrolerisdesignedbasedonthepredictivefunctionalcontrol.Theinternalmodelcontrolerisusedtomodifycontrolvoltageofpredictivefunctionalcontrol(PFC)toovercometheinterferenceofuncertaintyandimprovethecontrolsystemperformance.Simulationandexperimentalresultsshowthattheproposedcontrollercanmaketheballachievestablesuspensioninashorttimeandimprovetheanti-interferenceabilityandcontrolaccuracy.
Magneticlevitation;Railtransit;Industrialrobot;Predictivefunctionalcontrol;Neuralnetworkcontrol;Twodegreeoffreedom;Predictionerror;Internalmodelcompensation;Controlaccuracy
山西省自然科学基金(2014011020-1/2)、山西省研究生教学改革基金(20142058)、山西省研究生联合培养基地人才培养基金(2016JD35)、太原科技大学研究生科技创新基金(20145020)资助
孟凡斌(1989—),男,在读硕士研究生,主要从事预测控制、磁悬浮技术等方向的研究。E-mail:mfb0539@163.com。邵雪卷(通信作者),女,硕士,副教授,主要从事内模控制、智能控制等方向的研究。E-mail:sxj0351@163.com。
TH86;TP
ADOI: 10686/j.cnki.issn1000-0380.201701006
修改稿收到日期:2016-08-03

