Coulomb干摩擦模型与LuGre摩擦模型的分析与比较

王晓军

(常州工学院机械与车辆工程学院，江苏 常州 213032)

0 引言

摩擦这一非线性现象不可避免地存在于所有的机械系统当中。为了简化动力学模型，在建模、仿真和设计中往往忽略真实铰链的间隙、摩擦等因素。但随着机械系统运转速度、制造和控制精度的不断提高，需要用接近真实的方式描述物体间的接触与分离、黏滞与滑移(stick-slip)等现象。在研究对象的动力学方程中嵌入准确恰当的摩擦模型能够减少数值仿真结果与实验结果之间的误差[1]369，有效预测摩擦行为。

摩擦力是两个接触表面间相互的切向作用力，机械系统当中的摩擦与很多因素有关，它涉及接触力学、传热学、流体力学、化学、物理学、材料学、机械学等多学科知识，很难从机理上得到其准确的数学模型[2]，这也吸引着众多学者对其进行深入研究。动力学系统中干摩擦问题的研究已经持续了几个世纪，人们通过理论和实验建立的摩擦模型多达几十种，如Coulomb干摩擦模型、修正的Coulomb摩擦模型、黏性摩擦模型、Stribeck模型和LuGre摩擦模型等[3]。其中Coulomb干摩擦模型被认为是最简洁的摩擦模型[4-5]，但由于该模型的不连续性，给数值仿真分析带来很多困难；LuGre摩擦模型属于连续模型, 不同摩擦状态之间能够平滑地过渡, 因此逐步得到了应用[6]，但该模型的参数识别也是难点问题。本文针对Coulomb摩擦模型和LuGre摩擦模型进行分析，通过数值仿真比较这两种模型的适用性。

1 Coulomb摩擦模型

机械系统中常用的摩擦模型有多种，由于摩擦的复杂性，多数摩擦模型都是基于经验揭示摩擦的物理意义。16世纪初期，Leonardo da Vinci经过试验阐明摩擦力与法向接触力的正比关系，被法国物理学家Amontons所证实。1785年，Coulomb建立了不依赖滑动速度的摩擦定律，并对静摩擦力和动摩擦力做了明确的区分，建立了第一个摩擦模型[7]，该模型又可分为Coulomb干摩擦模型和修正的Coulomb摩擦模型，如图1所示。静态Coulomb干摩擦模型[8]可表示为

(1)

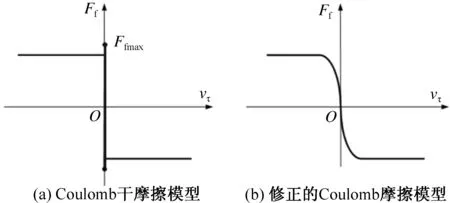
图1 Coulomb摩擦模型

(2)

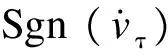
(3)

由式(1)和式(3)可以看出，当滑块的相对速度和相对切向加速度均为零时，接触点处于stick(黏滞)状态，其摩擦力的取值是一个范围。该摩擦模型形式简单，且动、静摩擦因数易于测定，因而得到了广泛的应用。

然而，Coulomb摩擦是关于接触点相对速度的非连续函数，且在相对速度为零时为多值函数，给含Coulomb干摩擦模型机械系统动力学方程的数值计算带来较大的困难[10]。为了避免数值计算方面的困难，提高计算效率，一些学者提出了多种修正的Coulomb摩擦模型，其中之一可表示为[1]373

(4)

式中cd动态矫正系数，可表示为

(5)

式中，v0和vT为给定的速度区间值。

修正的Coulomb摩擦模型是相对速度的连续函数，可用于无stick-slip运动状态切换的机械系统动力学的仿真。但是，该模型不能反映静摩擦特性(接触点相对速度为零时，摩擦力的取值是一个范围)，该模型在接触点的相对速度为零时其摩擦力也为零，这不符合实际的摩擦现象。

采用文献[27]三氯化铁-铁氰化钾试剂法对20%vol和72%vol红枣白兰地的致浊物进行定性分析，实验结果，均呈现明显的蓝色斑点。表明致浊物中含有酚类物质，所得结果与红外吸收光谱相吻合。

Flores利用L-N接触力模型、线弹性接触力模型和修正的Coulomb摩擦模型研究了含间隙转动铰和滑移铰机械系统的动力学建模与数值算法问题[8]，这些系统均存在stick-slip运动状态的切换。Pfeiffer等人[4，11]基于互补理论给出了单边接触含Coulomb干摩擦多体系统的动力学建模方法与数值计算方法；庄方方和王琪等人[12-14]分别研究了转动铰和滑移铰间隙充分小且含Coulomb干摩擦的平面多体系统的动力学建模与数值算法问题，应用试算法或线性互补方法，有效解决了stick-slip运动状态的切换问题。试算法适用于含摩擦接触点较少的机械系统，线性互补方法适用于含摩擦接触点较多的系统[10]105。基于线性互补理论的非光滑(含Coulomb干摩擦)系统的动力学建模与数值计算方法已被用于机械车辆等系统的动力学分析[9,15-16]。

2 LuGre摩擦模型

考虑到接触表面在外力作用下的变形，Dahl通过微分方程描述了摩擦力未达到最大静摩擦力之前界面的微小位移，Haessig和Friedland则从微观层面将接触面看成大量的弹性鬃毛，提出了鬃毛模型[6]207。基于鬃毛的平均变形，人们提出LuGre摩擦模型[1,3]，该模型可以描述为

(6)

其中,σ0为鬃毛的刚度，σ1为微观阻尼系数，σ2是黏性摩擦系数。鬃毛的平均变形可表示为

(7)

式中的函数g(vτ)描述了系统在克服静摩擦力之后开始运动，摩擦力在低速下随着速度的增加而减小的现象，即Stribeck现象。g(vτ)可表达为

(8)

式中，vs为Stribeck速度，γ(γ≥1)为依赖速度的摩擦力衰减梯度系数。

3 数值仿真算例

本文以滑块在主动力F(t)作用下在水平地面滑动为例(如图2所示)，分别用Coulomb干摩擦模型和LuGre摩擦模型描述滑块与地面间的摩擦力。

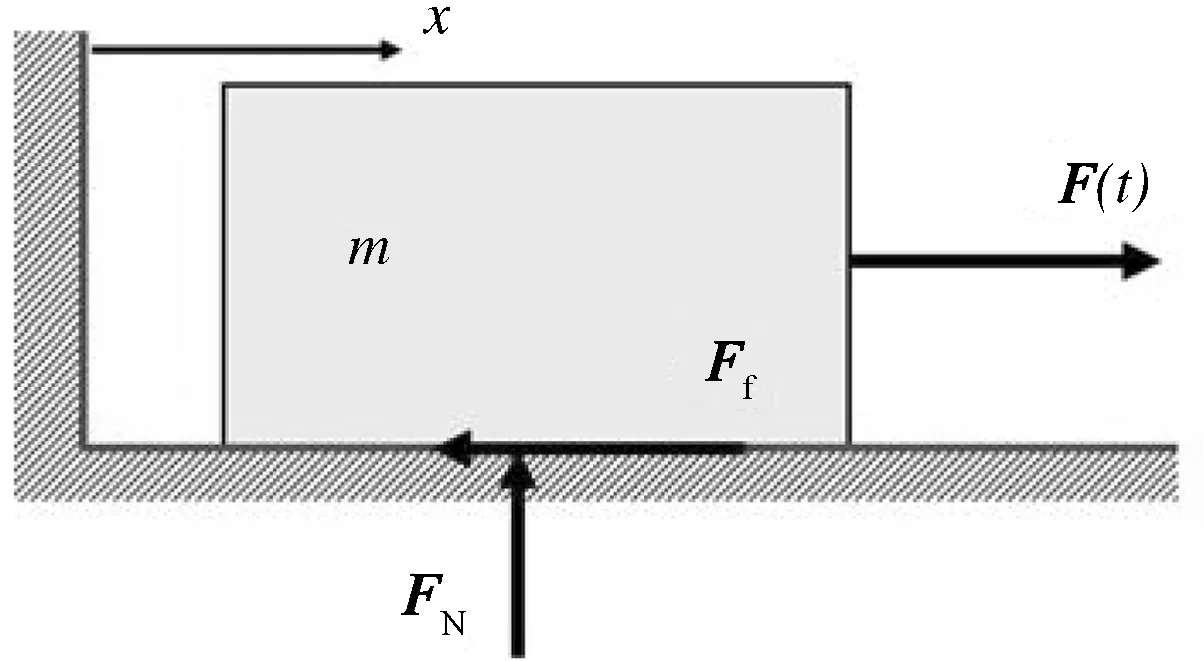
图2 算例中的系统

3.1 动力学方程

该系统的动力学方程为

(9)

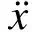
(10)

(11)

由该式不难看出，当物体处于stick状态或stick-slip状态切换时，方程(9)的等号两端均有加速度项，且式(11)是多值函数，其数值计算的难点在于物体的接触点处于stick状态或stick-slip状态切换时动力学方程的求解。本文用试算法判断接触点是否处于stick状态或stick-slip状态的切换。

当采用LuGre摩擦模型时，由式(6)—(8)可知，摩擦力可表示为

(12)

其动力学方程右端是关于系统状态变量的连续函数，便于数值求解。

3.2 数值仿真分析

系统参数如下：

m=2.0 kg;μ=0.5;μ0=0.75;g=10.0 N/kg;

F(t)=Asin(wt);w=4.0 rad/s;A=15.5 N;vs=0.0004;σ0=106;σ1=350;σ2=0.0;γ=2.0。

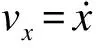
基于LuGre摩擦模型，图5给出了滑块的x、vx和Ff的时间历程图(粗实线为Ff，细实线为x，虚线为vx)。由图可见， LuGre摩擦模型同样能计算块体的stick-slip现象，并且在速度从零转变为非零时，摩擦力由静摩擦力向滑动摩擦力突变。由于两种模型的参数不同，关于速度和位移的计算结果不尽相同。

图3 x和vx的时间历程图

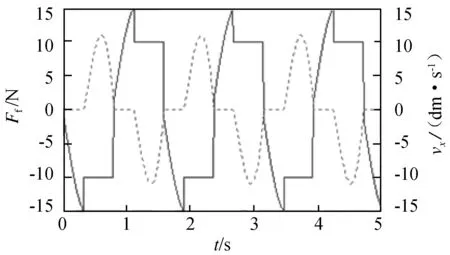
图4 vx和Ff的时间历程图

图5 x、vx和Ff的时间历程图

图6给出了σ0=105(其他参数不变)时滑块的x、vx和Ff的时间历程图(粗实线为Ff，细实线为x，虚线为vx)，由图可以看出，当摩擦力未达到最大摩擦力时，滑块就由静止开始滑动了，可见系统参数对LuGre摩擦模型的计算结果有很大影响。

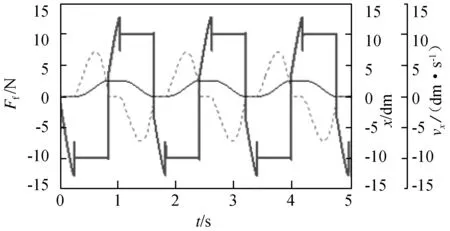
图6 当σ0=105时,x、vx和Ff的时间历程图

4 结论

本文分析比较了Coulomb干摩擦模型和LuGre摩擦模型的特点。Coulomb干摩擦模型形式简单，能较好地反映stick-slip运动状态的切换，摩擦参数易于通过实验测定，且在工程手册上可以查到不同材料间的动、静摩擦因数，但该模型的不连续性和多值性会给动力学方程的求解带来困难。LuGre摩擦模型是关于接触点的相对速度的连续函数，且与鬃毛的平均变形量等因素有关，在某种程度上能较好地反映摩擦的多种特性，但该模型与多个参数有关，其中有些参数不易测定，当某些参数选取得不合适时(如σ0)，则不能正确地反映摩擦现象。另外，由于σ0的值较大，在数值计算时需要取较小的步长才能进行求解，计算效率较低。文献[20—21]分析比较了多种摩擦模型，有助于进一步了解各种摩擦模型的特点。

[1]MUVENGEI O,KIHIU J,IKUA B.Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints[J].Multibody Syst Dyn,2012,28(4):369-393.

[2]BHUSHAN B.摩擦学导论[M].葛世荣，译.北京:机械工业出版社，2007.

[3]刘丽兰,刘宏昭,吴子英,等.机械系统中摩擦模型的研究进展[J].力学进展,2008,38(2)：201-213.

[4]PFEIFFER F,GLOCKER C.Multibody dynamics with unilateral contacts[M].New York:John Wiley & Sons.Inc，1996.

[5]FLORES P,AMBRSIO J， PIMENTA CLARO J C P，et al.Kinematics and dynamics of multibody systems with imperfect joints[M].Berlin：Springer,2008.

[6]丁千,翟红梅.机械系统摩擦动力学研究进展[J].力学进展，2013,43(1):112-131.

[7]MARQUES F,FLORES P， LANKARAN H M.On the Frictional Contacts in Multibody System Dynamics[M]//JOSEP M,FONT L.Multibody Dynamics Computational Methods and Applications.Switzerland:Springer International Publishing,2016:67-91.

[8]FLORES P,AMBRSIO J,CLARO J C P,et al.Translational joints with clearance in rigid multibody systems[J].Journal of Computational and Nonlinear Dynamics,2008,3:011007(1-10).

[9]PAULO F,LEINE R,GLOCKER C.Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach[J].Multibody Syst Dyn,2010,23(2):165-190.

[10]王琪,庄方方,郭易圆,等.非光滑多体系统动力学数值算法的研究进展[J].力学进展，2013,43(1)：101-111.

[11]PFEIFFER F,FOERG M,Uibrich H.Numerical aspects of non-smooth multibody dynamics[J].Computer Methods in Applied Mechanics and Engineering,2006,195:6891-6908.

[12]庄方方,王琪.含摩擦柱铰链平面多体系统动力学的建模和数值方法[J].工程力学，2012，29(5)：193-199.

[13]WANG Q,PENG H,ZHUANG F F.A constraint-stabilized method for multibody dynamics with friction-affected translational joints based on HLCP[J].Discrete and Continuous Dynamical Systems Series B，2011,16(2):589-605.

[14]ZHUANG F F,WANG Q.Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints[J].Multibody Syst Dyn,2013,29(4):403-423.

[15]王晓军,王琪.含摩擦与碰撞平面多刚体系统动力学线性互补算法[J].力学学报，2015,47(5):814-821.

[16]范新秀,王琪.车辆纵向非光滑多体动力学建模与数值算法研究[J].力学学报，2015,47(2):303-309.

[17]PENNESTRI E,VALENTINI P P,VITA L.Multibody dynamics simulation of planar linkages with Dahl friction[J].Multibody Syst Dyn,2007,17(4):321-347.

[18]MUVENGEI O,KIHIU J,IKUA B.Dynamic analysis of planar rigid-body mechanical systems with two-clearance revolute joints[J].Nonlinear Dyn,2013,73:259-273.

[19]WANG Z,TIAN Q,HU H Y,et al.Nonlinear dynamics and chaotic control of a exible multibody system with uncertain joint clearance[J/OL].Nonlinear Dyn,2016,86(3):1571-1597.[2017-10-20].https://link.springer.com/article/10.1007%2Fs11071-016-2978-8.DOI:10.1007/s11071-016-2978-8.

[20]MARQUES F,FLORES P,PIMENTA CLARO J C,et al.A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems[J].Nonlinear Dyn,2016,86(3):1407-1443.

[21]PENNESTRI E.ROSSI V,SALVINI P,et al.Review and comparison of dry friction force models[J].Nonlinear Dyn,2016,83(4):1785-1801.