基于簇特征的球员跑动大规模数据聚类研究
尹倩
(安徽体育运动职业技术学院,安徽 合肥 230051)
0 引言
足球运动是一项要求技术和速度能够很好结合的体育项目,足球技术要有跑动速度作为前提和保证。训练中,如果仅凭教练员肉眼和经验判断球员的跑动能力,则无法获取和挖掘跑动中瞬时加速度、最高速度等信息,难以分析球员的运动类型。
现有智能采集技术已成功应用于足球训练加速度信息采集[1],数据挖掘中的聚类研究算法亦广泛应用于多学科领域。然而,在足球训练数据采集过程中,球员跑动数据是动态变化的,且在整场比赛中产生的数据量是巨大的,因此如何对动态且巨量的数据样本快速高效地聚类成为本文研究重点。
传统聚类算法(基于划分的k-means、基于密度的DBSCAN算法等)只适合处理静态数据且算法复杂度高[2],难以针对大数据集和动态数据进行有效处理,为此产生增量聚类算法[3]。增量聚类在前期聚类结果基础上对新增数据逐个或批量处理,避免大量的重复计算,提高了聚类效率[4],数据量越大,增量聚类就越能体现出其优越性,且增量聚类算法适用于动态数据。
基于划分的k-means聚类算法适用于处理数值型数据,且对球形和凸型数据具有较好的聚类效果[5]117,能够辅助教练员挖掘分析运动员跑动类型,此处选择k-means聚类算法较为适合,但增量k-means聚类算法本质是基于距离的方法,当增量数据出现时易发生概念偏移现象,从而导致增量聚类算法与原有静态算法聚类结果不一致。已有的增量k-means聚类算法研究[5]117加入检测概念偏移环节来避免聚类结果不一致问题,但逐一检测单个新样本与原始聚类间概念偏移本身就是一个复杂和耗时的过程。
受上述启发,本文在相关研究基础上,引入簇特征[6-7]这一全局概念来快速检测和处理原始聚类各簇和增量数据之间的关系,从而避免逐一检测单个新数据样本与原始聚类间的概念偏移现象,提出一种基于簇特征的球员跑动大规模数据聚类方法并应用在实际训练领域。实验结果表明,该方法能快速高效处理动态增量数据,且聚类结果一致。
1 相关知识
1.1 概念偏移
k-means算法本质上是基于距离的算法,随着样本点的动态增加聚类结果将产生概念偏移。如图1所示,假使k=2,原始数据为数据点{1,2,3,4,5,6,7,8},原始聚类结果产生2个簇C1和C2,分别为{1,2,3,4,5}和{6,7,8}。随着增量数据点9和10的加入,此时采用增量聚类算法产生的两个簇应为{1,2,3,4,5}和{6,7,8,9,10},但是可以看到,此时的数据如果采用原始聚类算法结果为{1,2,3,4,5,6}和{7,8,9,10}。问题随之产生:为了减少算法复杂度而采用增量聚类算法,但是却造成数据结果不一致。随着大量增量数据的加入,聚类中心不断变化亦造成数据不断偏移。

图1 基于距离的聚类过程中概念偏移现象
1.2 簇特征
簇特征[6-7]CF可以表示为n元组,这里根据需要选择簇特征二元组,分别为表示簇Ci中心点的均值Omp(Ci)和簇中数据点凝聚程度的簇方差SSQ(Ci)。CF总结了各增量子簇个体的信息,是增量子簇的整体表示。
CF(Ci)=(Omp(Ci),SSQ(Ci))


1.3 概念偏移检测
数据概念偏移检测[8]主要关注聚类结果的簇中心偏移,簇方差反映了簇中各点与中心点的集散程度,其值越大表明簇中存在个别点与中心点距离越大,因此采用数据流研究中常用的计算两次增量聚类各簇方差SSQ变化来检测是否发生概念偏移。假设聚类类别k为3,设第1次数据所得的k个簇各簇特征的簇方差CF.SSQ={SSQ(C1),SSQ(C2),SSQ(C3)},随着增量数据到来,所得新的k个簇各簇特征的簇方差
CF(++).SSQ={SSQ(++)(C1),SSQ(++)(C2),SSQ(++)(C3)},设Δ=CF(++).SSQ-CF.SSQ,若Δ>ε,则发生概念偏移,反之没有发生概念偏移。参数ε根据情况设定。
2 基于簇特征的球员跑动大规模数据聚类算法模型
2.1 聚类样本和距离计算
原始数据为某小学校园足球10名球员(守门员除外)训练时通过数据采集装置采集到的三维加速度数据,如表1所示(篇幅有限,这里为3名球员在1 s内的20条记录)。从表中可以看到,球员1加速度最大达到7.15737 gn,这里gn取9.8 m/s2,该加速度约为70 m/s2。

表1 3名球员1 s内x、y、z三个方向瞬时加速度数据 gn
注:前后方向为x,左右方向为y,上下方向为z。
数据预处理将反方向加速度(负数)通过绝对值函数表示为加速度大小(正数),并采用加权加速度为x、y和z三个方向加速度绝对值之和表示其整体加速度水平[9]:
ALLsingal(IDi)t=ax+ay+az
(1)
式中,i为球员号码标识,取值为1~10。为保证瞬时性和灵敏度,3 min内即有3 600条记录。
球员IDi和IDj聚类距离
Dist(IDi,IDj)=ALLsingal(IDi)-ALLsingal(IDj)
(2)
因教练员希望从大量的瞬时加速度信息中挖掘发现各运动员的运动类型(积极进攻型、稳定型、消极被动型),因此采用k-means聚类算法较为合适(k值取3)。
2.2 聚类过程
聚类过程分两个阶段:初始聚类阶段和增量聚类阶段。
2.2.1 初始聚类阶段
原始数据预处理之后,采用传统k-means聚类算法得到原始数据聚类结果{C1,C2,C3},以及聚类后各簇特征CF(Ci)=(Omp(Ci),
SSQ(Ci))。
2.2.2 增量聚类阶段
步骤1:利用初始聚类阶段所得的簇特征,对每一个增量数据(对于大规模实时流式数据,为在可接受精度范围内提高聚类效率,增量数据可选取固定时间间隔内的数据[8],此处按照训练时长,t取3 min),计算每名球员在每3 min内加权加速度平均值,即该球员增量数据,此时的各中心点和簇方差为其簇特征CF(Ci)=(Omp(Ci),SSQ(Ci))。
步骤2:计算各球员此时的中心点与之前聚类阶段所得的各簇中心点的距离,将球员归为相应类别。例如3号球员,其增量时间间隔3 min的中心点和之前聚类结果积极进攻型距离较近,则将3号球员归为积极进攻型。逐个比较其他球员与之前聚类簇特征关系),同时计算并更新此时各簇特征CF(++)(Ci)=(Omp++(Ci),SSQ(++)(Ci))。
步骤3:利用本文1.3概念偏移检测算法检测是否发生概念偏移。如发生概念偏移,则重新聚类,并保存此聚类结果簇特征为原始聚类簇特征CF(Ci)=(Omp(Ci),SSQ(Ci))。接着执行步骤2,循环处理,直至所有增量数据处理完毕。
步骤4:保存最终聚类结果,该结果即为实时且无概念偏移的正确聚类结果。
2.3 算法模型图
为更好地将本算法与传统k-means算法时间复杂度和聚类结果对比,图2给出了算法模型及具体步骤。

图2 算法模型图
3 实验及应用
3.1 实验数据
实验数据来源于本文作者在体育科学领域的研究课题,将传感器绑定至足球运动员小腿部位,监测其瞬时三维加速度。三维加速度传感器在整场45 min的训练过程中约有54 000条记录。增量数据为每3 min获取每名球员加速度信息3 600条记录。
3.2 本方法与传统的方法耗时比较
设聚类结果获得簇数为k,每时间间隔为t,整个训练时长45 min,获取数据记录累计为m条(这里m为54 000),球员数量为n(这里除守门员之外为10人)。

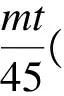
从以上结果看出,开始3 min,本算法对原始数据采用传统k-means聚类算法得到原始聚类结果,此时两个算法时间复杂度一致。另外,本算法在第30 min时刻检测到概念偏移,并重新进行聚类,此刻时间复杂度与传统算法亦一致,其余时间段均无概念偏移发生,检测概念偏移和增量聚类时间复杂度均近似为0。

图3 本算法与传统算法聚类耗时比较
3.3 本方法与传统算法聚类结果一致性比较
为验证本方法与传统方法聚类结果一致性,采用相同的聚类距离阈值对原始数据和增量数据处理,传统算法对10名球员各54 000条记录聚类结果为{(1,4),(3,5,2,9,6),(7,8,10)}。
本文算法先采用分时间间隔选取增量数据的方法,然后在原始聚类结果上采用基于簇特征的球员跑动大规模数据聚类算法,故整个聚类过程是一个不断变化的过程,由于本文引入数据概念偏移检测环节,故聚类过程虽动态变化但最终结果亦与传统算法结果一致。详见图4。
综上看出,本文提出的基于簇特征的球员跑动大规模数据聚类研究算法在保证聚类结果一致的前提下,能够快速地处理实时采集到的足球运动员跑动大规模动态数据。
4 结语
本文从足球运动员跑动的动态数据的特点和实时分析聚类挖掘不同运动员跑动类型的需求出发,针对传统k-means聚类算法对动态数据聚类需要每次都进行整个数据集的聚类而导致聚类效
率低下的问题,提出簇特征这一全局概念进行k-means增量聚类,该算法首先利用k-means算法进行初始聚类,保留聚类后得到的簇特征,当增量数据到来时,仅需要利用簇特征对它们采用增量算法聚类,而无需全部聚类,故有效降低时间消耗。更重要的是,k-means算法基于距离的本质导致数据易发生概念偏移,基于簇特征的方法使检测概念偏移的时间近似为零,故在与传统聚类算法结果一致的前提下,整体时间较传统算法大大降低。但也看到,目前的数据概念偏移检测方法是一种相对比较简单的方案,还需在更大的数据集上进一步实验验证。
[1]房霄.足球运动数据采集系统设计[D].南京:南京理工大学,2010.
[2]李滔,王士同.适合大规模数据集的增量式模糊聚类算法[J].智能系统学报,2016,11(2):187-198.
[3]陶舒怡.基于簇相合性的文本增量聚类算法研究[D].南昌:江西师范大学,2013.
[4]黄德才,李晓畅.基于相对密度的混合属性数据增量聚类算法[J].控制与决策,2013,28(6):815-822.
[5]胡伟.一种改进的动态k-均值聚类算法[J].计算机系统应用,2013,22(5).
[6]潘敏,王明文,王晓庆,等.基于簇特征的文本增量聚类研究[J].江西师范大学学报(自然科学版),2014,38(1):95-101.
[7]孟海东,王淑玲,郝永宽.基于簇特征的增量聚类算法设计与实现[J].计算机工程与应用,2010,46(24):132-134.
[8]李子柳.大数据实时流式聚类处理框架研究[D].广州:中山大学,2013.
[9]钟君.基于加速度传感器的日常行为识别的特征提取方法研究[D].兰州:兰州大学,2016.

