一种高斯区间核SVM分类模型*
王文剑 祁晓博 郭虎升
(1.山西大学计算机与信息技术学院,太原,030006;2.山西大学计算智能与中文信息处理教育部重点实验室,太原,030006)
一种高斯区间核SVM分类模型*
王文剑1,2祁晓博1郭虎升1
(1.山西大学计算机与信息技术学院,太原,030006;2.山西大学计算智能与中文信息处理教育部重点实验室,太原,030006)
区间型数据(Interval data, ID)是属性特征取值为区间的一类数据,针对区间型数据的分类问题,本文提出一种高斯区间核支持向量机分类模型(Support vector machine based on Gauss interval kernel, GIK_SVM)。该方法引入半宽因子,在区间型数据的中值与半宽度之间进行折中,并据此构造高斯区间核用以衡量两个区间型数据间的相似性,然后用SVM模型进行分类。在人造数据集和真实数据集上的实验结果表明,本文提出的算法对区间数据有更好的分类性能。
区间型数据; 半宽因子; 区间核; GIK_SVM模型
引 言
随着互联网与信息技术的迅猛发展,数据的获取与使用逐渐便捷,不仅数据量每年都在飞速增长,数据的复杂性也日趋明显[1,2]。其中有一类数据与人们的生产、生活息息相关,如某一地区一段时间的气温变化、某一段时间内的交通流量和工业总产值增长率等,这类数据的特点是:每个属性特征的取值不确定,而是一个区间,这类数据称为区间型数据。这类数据的出现可能是由于属性值的多次测量、置信区间估计或取值范围有界等。相较于离散数据,区间型数据可以从全局把握数据对象的内在结构特征,更有利于揭示隐含在数据内部的规律。因此,区间型数据可以表示数据的不确定性和可变性,在决策支持中具有重要的应用价值。与离散数据(确定性数据)不同,目前关于区间型数据的处理方法主要有3大类。(1)模糊集方法[3],这类方法通过计算元素关于集合的隶属程度来近似描述不确定性,将每个区间离散化为一个确定值(通常是符号属性数据),再用传统方法进行处理。这类方法中隶属函数大多为专家凭经验给出,带有强烈的主观意志。(2)中值法[4],即用区间中值作为区间型数据的特殊点,再用传统方法进行处理。该方法只考虑了区间型数据的内部情况,丢失了区间大小这一相关信息。(3)采用上下边界值替代区间型数据[5-7],即将区间型数据离散化为两个确定性数值,再用传统方法进行处理。这类方法只用上下边界值进行计算,未考虑区间型数据的内部分布情况。因此又有学者提出改进方法,在上下界基础上考虑中值信息[8-10],这样不仅考虑到区间边界,还将内部分布一并融合进去,使区间型数据表示更加全面。文献[8]利用区间中值与宽度表示区间型数据,运用传统的回归方法分别对区间中值与区间半宽度生成回归方程,然后通过这两个方程对区间上下限进行预测。文献[9]用区间中值与宽度表示区间变量,在这两个独立的确定性变量上用对称线性回归模型进行预测。文献[10]提取区间值数据的区间中值与宽度,分别作为Gauss分布函数的期望和方差,用Gauss分布函数表示区间值数据并对其进行相似度量。
目前关于区间型数据的处理主要集中在聚类和回归分析中[4-11],分类问题的研究相对较少[12]。考虑到区间型数据的特点及支持向量机(Support vector machine, SVM)良好的泛化能力[13-14],本文提出一种高斯区间核SVM分类模型。该模型采用区间中值与半宽度表示区间型数据,设计了一个可调的半宽因子,并构造了高斯区间核,进而利用高斯区间核SVM模型对区间型数据进行分类。
1 基于高斯型区间核的SVM分类模型
1.1 高斯区间核
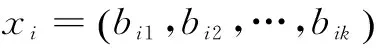
(1)
(2)
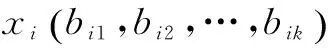
(3)
其中
(4)
(5)
联立式(3~5),可得
(6)

1.2 算法的主要步骤
算法1 GIK_SVM算法
(1) 根据式(1,2)分别计算出Tr和Te上区间型样本的区间中值与区间半宽度;
(2) 根据式(6)在训练集Tr上计算高斯区间核矩阵;
(3) 根据所得高斯区间核矩阵建立SVM分类模型,并在Te上进行测试;
(4) 算法结束。
将本文算法与基于区间中值的SVM分类算法(Supportvectormachinebasedonintervalmedian,IM_SVM)和基于区间边界值的SVM分类算法(Supportvectormachinebasedonintervalboundaryvalue,IBV_SVM)进行比较,其中,IM_SVM算法只考虑区间型数据中值这一主要因素,IBV_SVM算法只考虑区间的上下两个边界值,两种算法的主要步骤分别如下。
算法2 IM_SVM算法
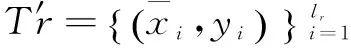
(2) 用传统高斯核在新的训练集T′r上计算高斯核矩阵;
(3) 根据所得高斯核矩阵建立SVM分类模型,并在T′e上进行测试;
(4) 算法结束。
算法3 IBV_SVM算法
(2) 用传统高斯核在新的训练集T′r上计算高斯核矩阵;
(3) 根据所得高斯核矩阵建立SVM分类模型,并在T′e上进行测试;
(4) 算法结束。

2 实验结果及分析
2.1 实验环境及实验数据
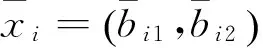
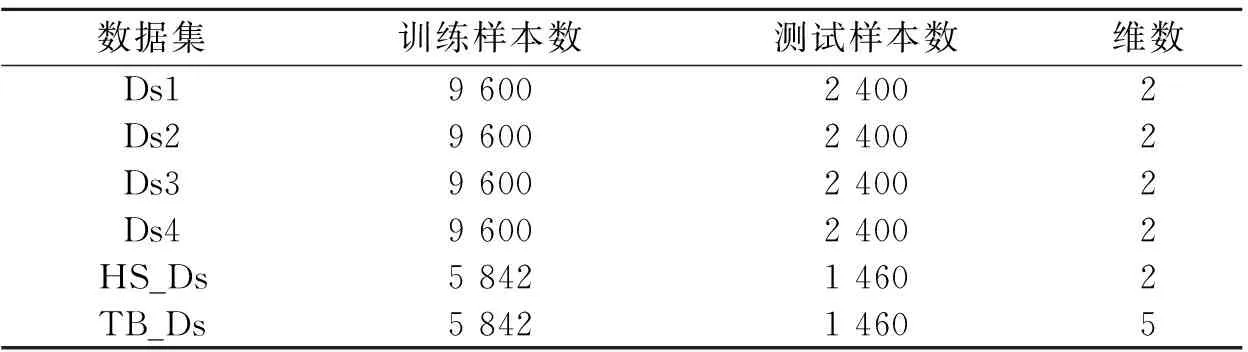
表1 实验使用的数据集
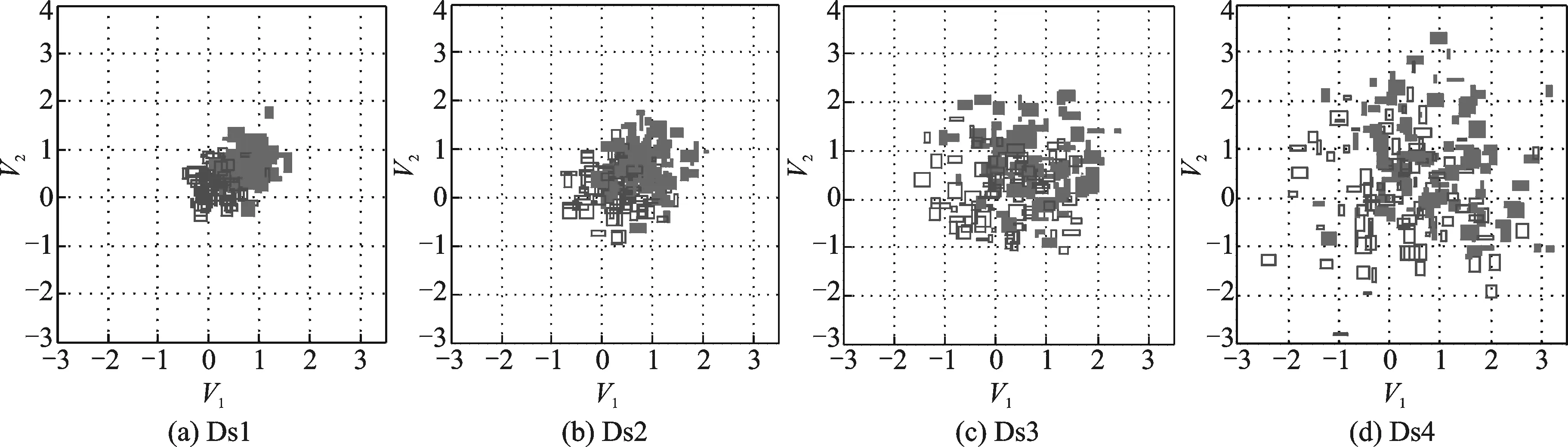
Fig.1 Distributions of artificial datasets
2.2 半宽因子对算法的影响
本实验中,TB_Ds上σ=0.1,在其他数据集上σ=0.25。为简单起见,本文实验中令α1=α2=…=αk=α,用α来表示半宽因子。图2为3种算法预测准确率随α变化的实验结果。由图2可以看出IM_SVM算法和IBV_SVM算法与半宽因子α值无关,所以其准确率曲线不发生变化。GIK_SVM的预测准确率随着半宽因子α的调整不断变化,在Ds1上,GIK_SVM整体优于另两种算法,在α=0.05处,取到最优准确率;在Ds2上,GIK_SVM介于另两种算法之间,在α=0.01处,GIK_SVM算法的准确率也达到了最优值;在Ds3与Ds4这两个数据集上,GIK_SVM浮动较大,Ds3中,在α=0.1与α=0.75处,GIK_SVM算法的准确率优于另两种算法,且当α=0.75时,达到最优;在Ds4中,当α=0.025时,GIK_SVM虽与IM_SVM算法十分接近,但仍取到最优准确率。从这4个图中也能看出,除Ds2外,本文算法的最优准确率明显高于另外两个算法。从它们的分布来看,Ds1中两类数据分布紧密,但界限很清晰;Ds3与Ds4中则是混合重叠较多,数据较分散;而Ds2中两类数据不仅分布紧密,还混合重叠较多,这也造成了GIK_SVM方法的分类准确率不如在其他人造数据集上效果好,且不如IBV_SVM方法准确率高。IM_SVM算法在两个人造数据集上的准确率优于IBV_SVM算法,而在另外两个人造数据集上的准确率则不如IBV_SVM算法。由于人造数据集的构造方法较简单,使得本文算法与另两种算法在人造数据集上的比较结果相差并不大,因此,本文又在真实数据集上进行了实验。

图2 3种算法的预测准确率随α变化的实验结果Fig.2 Experimental results of the prediction accuracy with α for three algorithms

2.3 参数σ对算法的影响
本实验主要考察参数σ对算法的影响。选取图2中GIK_SVM的最优准确率对应的α值作为本实验各数据集的默认α值,图3为3种算法预测准确率随σ变化的实验结果。由图3可以看出不同的σ值对准确率的影响很大。当σ<2时,在Ds1与2个真实数据集上,GIK_SVM预测准确率较高;在其余数据集上,3种算法的准确率相当。当σ>2时,3种算法的准确率都开始降低。在Ds1上,GIK_SVM仍优于另外两种算法;在HS_Ds上,GIK_SVM介于另两种算法之间;在TB_Ds上,3种算法的准确率相当;在其他3个数据集上,IBV_SVM算法准确率快速降低,GIK_SVM与IM_SVM算法准确率大体一致。目前关于高斯核参数σ的优化已有很多研究,而本文主要关注高斯区间核度量区间型数据相似性的有效性,所以未对σ进行进一步优化,后续实验中,本文选取σ<2的值。
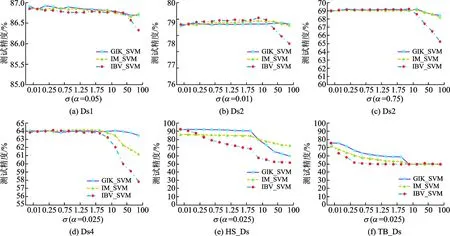
图3 3种算法预测准确率随σ变化的实验结果Fig.3 Experimental results of prediction accuracy with σ for three algorithms
2.4 本算法与决策树模型的比较
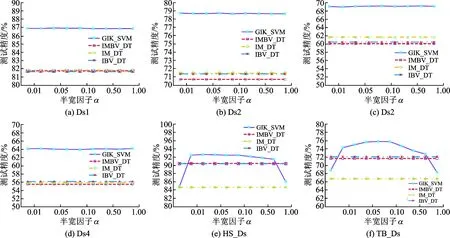
图4 GIK_SVM与决策树模型预测准确率随α值变化的实验结果Fig.4 Experimental results of prediction accuracy with α for GIK_SVM and decision tree models
为了进一步验证GIK_SVM算法的有效性,本文还与3种决策树模型进行比较。基于中值半宽的决策树模型(Decisiontreebasedonintervalmedianandboundaryvalue,IMBV_DT)将中值与半宽度分别作为判别属性;基于中值的决策树模型(Decisiontreebasedonintervalmedian,IM_DT)只将中值作为判别属性;基于边界值的决策树模型(Decisiontreebasedonintervalboundaryvalue,IBV_DT)将区间的上下边界值作为判别属性。本实验中,TB_Ds上σ=0.1,在其他数据集上σ=0.25。图4为GIK_SVM算法与决策树模型预测准确率随α值变化的实验结果。由图4可以看出GIK_SVM算法的准确率明显高于3种决策树模型,其准确率高出5%~9%左右。在4个人造数据集上,GIK_SVM方法准确率曲线都高于其余3条曲线,决策树模型的3条曲线则比较邻近。在两个真实数据集上,除去α取到边界值0和1时,GIK_SVM算法的准确率也都明显比决策树模型高,即使在边界值上,GIK_SVM的准确率仍高于IM_DT算法。实验结果最终表明,SVM模型优于决策树模型。
3 结 论
区间型数据是一类常见然而较为特殊的数据形式,目前关于区间型数据处理的高效分类方法研究还相对较少。本文通过引入半宽因子,很好地折中了区间中值与区间半宽度对区间型数据挖掘的影响,此外构建了高斯区间核,并用高斯区间核SVM模型对区间型数据进行分类,提高了分类预测性能。在后续研究中,将考虑针对不同的区间型特征值,选取不同的半宽因子,以取得更好的效果。另外,将探索构造更多的有效区间核,进一步提高处理区间型数据的有效性。
[1] 何清, 李宁, 罗文娟, 等. 大数据下的机器学习算法综述[J]. 模式识别与人工智能, 2014, 27(4): 327-336.
HeQing,LiNing,LuoWenjuan,etal.Asurveyofmachinelearningalgorithmsforbigdata[J].PattemRecognitionandAitificialIntelligence, 2014, 27(4): 327-336.
[2] 潘志松, 唐斯琪, 邱俊洋, 等. 在线学习算法综述[J]. 数据采集与处理, 2016, 31(6): 1067-1082.
PanZhisong,TangSiqi,QiuJunyang,etal.Surveyononlinelearningalgorithms[J].JournalofDataAcquisitionandProcessing, 2016, 31(6): 1067-1082.
[3] 胡凯, 孟广武, 于西昌. 区间值模糊集上的上(下)近似[J]. 模糊系统与数学,2007, 21(1): 123-127.
HuKai,MengGuangwu,YuXichang.Upper(lower)approximationofaninterval-valuedfuzzyset[J].FuzzySystemandMathematics, 2007, 21(1): 123-127.
[4]BillardL,DidayE.Regressionanalysisforinterval-valueddata[C]//DataAnalysis,ClassificationandRelatedMethods,ProceedingsoftheSeventhConferenceoftheInternationalFederationofClassificationSocieties(IFCS’00).Berlin,Heidelberg:Springer-VerlagPress, 2000: 369-374.
[5]BillardL,DidayE.Symbolicregressionanalysis[C]//Classification,ClusteringandDataAnalysis,ProceedingsoftheEighthConferenceoftheInternationalFederationofClassificationSocieties(IFCS’02).Berlin,Heidelberg:Springer-VerlagPress, 2002: 281-288.
[6]CabanesG,BennaniY,DestenayR.Anewtopologicalclusteringalgorithmforintervaldata[J].PatternRecognition, 2013,46(11):3030-3039.
[7]CarvalhoFDATD.AfuzzyclusteringalgorithmforsymbolicintervaldatabasedonasingleadaptiveEuclideandistance[C]//Proceedingsofthe13thInternationalConferenceonNeuralInformationProcessing(ICONIP2006).Berlin,Heidelberg:Springer-VerlagPress, 2006: 1012-1021.
[8]LimaNetoEDA,DeCarvalhoFDAT.Centreandrangemethodforfittingalinearregressionmodeltosymbolicintervaldata[J].ComputationalStatisticsandDataAnalysis, 2008, 52(3):1500-1515.
[9] Domingues M A.O, Souza R M C R D, Cysneiros F J A. A robust method for linear regression of symbolic interval data[J]. Pattern Recognition Letters, 2010, 31:1991-1996.
[10]吕泽华, 金海, 袁平鹏, 等. 基于Gauss分布函数的区间值数据的模糊聚类算法[J]. 电子学报,2010,38(2):295-300.
Lü Zehua, Jin Hai, Yuan Pingpeng, et al. A fuzzy clustering algorithm for interval-valued data based on gauss distribution functions[J]. Acta Electronica Sinica, 2010, 38(2): 295-300.
[11]于洋, 张颖, 胡舒涵. 区间型数据聚类的FCM新算法[C]//中国通信学会第六届学术年会论文集(下).北京:中国通信学会,2009: 249-253.
Yu Yang, Zhang Ying, Hu Shuhan. The new FCM algorithm of interval data clustering[C]//Proceedings of the 6th Academic Annual Conference of China Communication Association. Beijing: China Institute of Communications Press, 2009: 249-253.
[12]陈建凯, 王鑫, 何强, 等. 区间值属性的单调决策树算法[J]. 模式识别与人工智能, 2016, 29(1): 47-53.
Chen Jiankai, Wang Xin, He Qiang, et al. Interval-valued attributes based monotonic decision tree algorithm[J].Pattem Recognition and Aitificial Intelligence, 2016, 29(1): 47-53.
[13]Vapnik V. Statistical learning theory[M]. New York: Springer-Verlag Press, 1998:493-520.
[14]Cortes C, Vapnik V. Support vector networks[J]. Machine Learning, 1995(20): 273-297.
[15]中国6603个居民点天气[EB/OL]. http://rp5.ru/中国天气_, 2016-04.
Support Vector Machine Classification Model Based on Gauss Interval Kernel
Wang Wenjian1,2, Qi Xiaobo1, Guo Husheng1
(1.School of Computer and Information Technology, Shanxi University, Taiyuan, 030006, China; 2.Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan, 030006,China)
Interval data (ID) is a kind of data which the attribute values are the interval. Aiming at the classification problem of interval data, a support vector machine classification model based on Gauss interval kernel (GIK_SVM) is proposed. In the method, the half-width factor is introduced which makes a compromise between the median and the half width of interval data. Then, the Gauss interval kernel is constructed to measure the similarity between two interval data. SVM model is applied to classify the samples.Experiment results on artificial and real datasets demonstrate that the proposed GIK_SVM has a better classification performance for interval data.
interval data(ID); half-width factor; interval kernal; GIK_SVM model
国家自然科学基金(61673249, 61503229, 61273291)资助项目;山西省回国留学人员科研项目(2016-004)资助项目;山西省自然科学青年基金(2015021096)资助项目;山西省高等学校科技创新(2015110)资助项目。
2016-11-30;
2017-01-07
TP18
A

王文剑(1968-),女,博士,教授,研究方向:神经网络,支持向量机,计算智能和数据挖掘, E-mail:wjwang@sxu.edu.cn。
祁晓博(1992-),女,硕士研究生,研究方向:机器学习和数据挖掘。

郭虎升(1986-),男,博士,副教授,研究方向:支持向量机,机器学习和数据挖掘。

