基于两种模型的测量中圆形地物位置及大小的确定

赵俊光 刘继权

(招远市灵山金矿，山东 招远 265402)

基于两种模型的测量中圆形地物位置及大小的确定

赵俊光 刘继权

(招远市灵山金矿，山东 招远 265402)

针对测量中观测的反映圆形地物形状的碎部点坐标，分别采用了直角坐标方程和参数坐标方程两种形式，通过两次平差，进行了圆的位置及大小计算，并进行了精度评定，结果表明，第一次平差的结果，两者相差较大，第二次平差的结果，两者相差不大。

圆形建筑物，间接平差，直角坐标方程，参数方程

在工程测量中，圆形地物非常多，如楼房、道路、花坛、水塘等，经常需要确定它们的位置及大小。本文中，分别基于圆的直角坐标方程形式和参数坐标方程形式，计算了圆形地物的位置及大小，并给出了精度评定。结果表明，本文的结论是有益的。

1 平差的数学模型

已知圆上m个点的观测值(Xi，Yi)(i=1,2,…，m),设为等精度观测，则利用直角坐标方程形式和参数坐标方程形式计算的函数模型形式如下。

1.1 直角坐标形式的函数模型

圆曲线的直角坐标方程以平差值表示为:

(1)

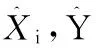
将式(1)线性化，则：

(2)

式(2)可视为附有参数的条件方程。

1.2 参数坐标形式的函数模型

圆曲线的参数方程以平差值表示为:

(3)

将式(3)线性化，则得误差方程:

(4)

式(4)中:

(5)

1.3 精度评定公式

单位权方差估值公式:

(6)

平差参数的协因数阵:

(7)

平差参数的协方差阵:

(8)

2 实验计算

2.1 观测数据

如表1所示，为同精度观测的某圆形建筑物的若干点坐标。

表1 所观测的点坐标 m

2.2 数据计算

1)依据直角坐标方程形式。在表1中，采集了6个点坐标。为了确定一个圆方程，至少需要3个点坐标，因此，计算时需要列出3个附有参数的条件方程。代入相关数据，计算得出圆心坐标(75.885 9,105.887 8)，半径为11.061 0。

依据式(8)，求得了参数a，b，r的第一次平差的中误差分别为σa=0.083 3 m，σb=0.092 0 m，σr=0.124 2 m。

进行了第二次平差后，得圆心坐标(75.886 1,105.879 9)，半径11.062 4；参数a，b，r的中误差分别为σa=0.001 417 m，σb=0.001 563 m，σr=0.002 11 m。

2)依据参数坐标方程形式。在表1中，采集了6个点坐标。则总观测数n=12，t=9，则利用间接平差原理，依据式(4)，需要列出12个误差方程。通过计算，可得出圆心坐标(75.548 2,105.483 1)，半径为11.003 3。

依据式(8)，求得了参数a，b，r的第一次平差的中误差分别为σa=0.044 4 m，σb=0.039 9 m，σr=0.029 3 m。

进行了第二次平差后，得圆心坐标(75.890 2,105.879)，半径11.052 4；参数a，b，r的中误差分别为σa=0.004 64 m，σb=0.004 174 m，σr=0.003 07 m。

3 结语

通过以上计算可以看出，第一次平差后，两种模型计算的结果相差较大；第二次平差后，两种模型计算的结果相差较小；由此证明了两种模型的通用性。

[1] 王 永.利用Excel绘制误差椭圆的方法[J].矿山测量，2008(2)：15-17.

[2] 苗元欣.基于一元线性回归的变形监测数据处理与分析[J].山西建筑，2013，39(33)：206-207.

[3] 泥立丽.基于Excel的绘制误差曲线的方法[J].矿山测量，2010(4)：50-51.

[4] 刘洪晓.基于BP神经网络的变形监测数据处理与分析[J].科技视界，2014(11)：99-102.

[5] 高腾飞.L波段D-InSAR在矿区地面沉降监测中的应用[J].中国科技论文，2016(4)：80-81.

Determination of circular ground feature location and size in measurement based on two models

Zhao Junguang Liu Jiquan

(ZhaoyuanLingshanGoldMine,Zhaoyuan265402,China)

According to the detail point coordinate reflection of ground feature shape observed in measurement, respectively using rectangular coordinate equation and parameters coordinate equation two forms, through the double adjustment, made the position and size calculation of circle, and made accuracy evaluation, the results showed that the first adjustment results, both had larger differences, second adjustment results, both had little differences.

circular building, indirect adjustment, rectangular coordinate equation, parametric equation

1009-6825(2017)01-0222-02

2016-10-25

赵俊光(1972- )，男，助理工程师

TU198

A