基于亚采样点级别的TDOA时延估计

杨建辉，王逸轩，刘玉红

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

基于亚采样点级别的TDOA时延估计

杨建辉，王逸轩，刘玉红

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

针对无源时延定位技术中时延的估算受系统采样率影响较大的问题，提出一种基于亚采样点的时延估计算法，在采样点最小单位的基础上，利用2个基准监测站信号点的几何特征计算时延。在Matlab仿真程序中，模拟1个信号辐射源和2个基准监测站，以2个监测站信号及其瞬时相位作为算法输入部分，对比二者时延估计的精度，证明算法的有效性。试验结果表明，基于亚采样点的时延估计算法计算精度与信号点数及采样周期有关，且在相同采样率下，该算法估计的时延精度高于采样点级别的时延估计方法。

TDOA；时延估计；亚采样点；瞬时相位法；精度分析

0 引言

无源时延定位(TDOA)利用检测信号到达已设定监测站之间的时间差来进行目标定位。检测信号到2个监测站的时间差折算成一个固定的距离差，根据双曲线定义，信号辐射源在以2个监测站为焦点的双曲线上。再添加1个监测站，可形成另外一条双曲线，2条双曲线的交点，即为信号辐射源的位置[1]。由于TDOA方法具有较高的定位精度、能够对宽带低谱密度无线电信号进行定位、系统易于组网等优势[2]，被国内外学者广泛研究，并取得了诸多成就。

目前TDOA时延估计方法中，最经典的广义互相关法，因其具有抗噪声能力强、计算简单和适用性广等优点被国内外学者广泛采用[3]，文献[4-5]使用广义互相关算法进行时延估计，但该方法在使用傅里叶变换计算互相关函数峰值时，容易出现谱泄露问题[6]，且其估计精度受系统采样率影响较大，采样率过大，很难得出较好的相关结果，采样率过小，估算误差难以接受，算法表现出一定的局限性。

本文在亚采样点基础上提出一种新的时延估计算法，分析2个监测站接收信号的时延与信号采样间隔的关系，并做进一步仿真试验，为实际无源时延定位的应用提供一种可行的时延估计算法。

1 双曲线定位原理

TDOA无源时延定位原理示意图如图1所示，A、B、C三个监测站(A为主站)分别设在不同的区域，同步接收由T信号源发出的无线电信号。通过相关算法计算出检测信号到2个监测站的时间差ΔTAB和ΔTAC，折算成距离差，由距离差可以画出2条双曲线RS和MN，2条双曲线的交点T即为辐射源的位置[7]。

图1 TDOA定位原理

假设3个监测站的坐标分别为A(x1,y1)，B(x2,y2)和C(x3,y3)，检测信号到达3站的时间分别为t1、t2和t3，待测信号辐射源的位置为T(x,y)，根据各点的几何关系，则有下式成立：

(1)

式(1)是由观测时延转换出来的2个距离差，c为空气中的光速，由此确定2条双曲线，即可进行辐射源的目标定位[8]。

在式(1)中，时延的计算是一个关键点也是难点。传统计算时延的经典方法广义互相关法，根据2个监测站接收信号的相关性[9]来进行时延估计，但该方法的最大时延估计精度为采样点级别。换言之，它能估算的最小时延为1/Fs[10]。若系统采用250kHz的采样率，估计的最大时延精度为4μs，以光的传播速度折算成距离为1 200m，这个精度对TDOA是灾难性的。即使采样率提高到6.25MHz，估计精度也只为48m，并且系统采样率不能无上限增加。因此为了使信号时延估计达到更高的精度，挖掘亚采样点的时延估计方法很有必要。

2 亚采样点时延估计的基本方法

2.1 基本方法原理

不同监测站接收的无线电信号，因其存在时间差，时域信号表现出明显的波形差异性。用Matlab仿真2路时延信号，两信号相差一个采样点，如图2所示，横轴为信号时间，纵轴为归一化的信号幅值，结合时域信号波形曲线的几何特性，说明亚采样点时延估计的基本方法。

图2中，以采样周期间隔为单位，y1(n)、y1(n-1)和y2(n)三个点构成一个直角三角形。这2个信号的时延如图中“Delay”所示，它构成直角三角形的一条直角边，用d表示为y1(n)y2(n)构成直角三角形的另一条边，y1(n)y1(n-1)与y1(n-1)y2(n)的夹角为θ。

图2 亚采样点基本方法

由图2中几何关系可知：

tanθ=d/Delay,

(2)

(3)

式中，Ts为信号的采样间隔。上述算法在Matlab中可表述为：

dy1=diff(y1)/Ts

dy=y1(2∶end)-y2(2∶end)

Delay=dy./dy1

上述程序中，对2个序列的所有离散点都进行一次时延估计，将估计的时延结果存储在数组Delay中，对Delay数组元素取平均即得到估计的2路信号时延值。

2.2 仿真分析

Matlab仿真中，模拟建立2个监测站和1个信号辐射源，辐射源产生信噪比为60dB的正弦波，监测系统采样间隔为0.01s，取100个采样点，设定2个监测站接收信号的时延为0.001s，如图3所示，显然该2路信号时延处于亚采样点级别。以2个监测站接收的信号S1和S2序列作为基本方法的输入部分，此时计算出两信号时延Delay=0.001 010 6s。

图3 亚采样点基本方法时延估计结果(SNR=60 dB)

通过仿真测试发现，该方法虽然是从相差1个采样点的情况推导而来，但是针对亚采样点的情况依然有效，其时延估算结果与真实值较为接近，估计误差仅为1.06%。

根据时延估算经验，其计算精度与接收信号的信噪比有直接关系，当信噪比低于某阈值时，任何方法都将无法进行时延估计。降低上述模拟产生信号的信噪比，继续观察实验结果，得出基本方法可估算时延的信噪比容忍下限。当模拟产生信噪比为30dB的正弦波时，采用基本方法估计时延结果如图4所示。

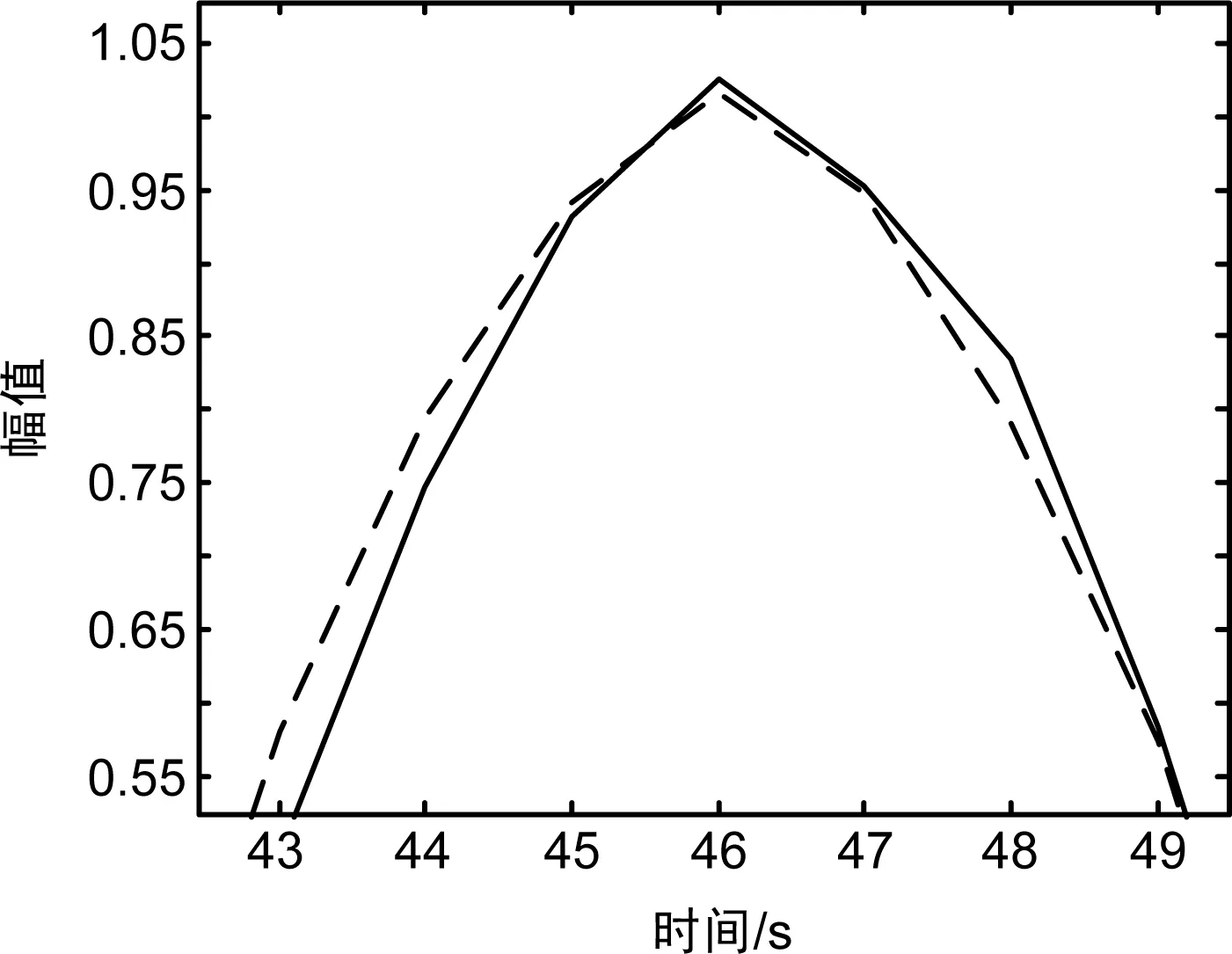
图4 亚采样点基本方法时延估计结果(SNR=30 dB)

进行多次仿真试验，发现该方法对噪声比较敏感。当接收信号的信噪比低至30dB时，估算出时延Delay=0.002 880 8s，误差为188.08%，该误差值已经无法被容忍。认为上述基本方法可有效估算时延的信噪比容忍下限为30dB。

本文将这种方法暂称为基本方法，因为它针对的是原始信号的直接比较。而原始信号通常是解调后的基带信号，这种信号的波动比较大，计算时延会有较大的误差[11]。根据经验，信号的瞬时相位比信号的波动要平缓很多，因而继续挖掘信号的瞬时相位作为时延估计的样本，力争得到更鲁棒的时延估计方法。

3 亚采样点时延估计的瞬时相位法

3.1 瞬时相位法及仿真分析

由于信号的瞬时相位是连续且平缓变化的[12]，尝试将其作为基本方法的输入部分，由此衍生出时延估计的瞬时相位法。在Matlab中计算信号的瞬时相位较简单，直接用以下语句即可得之：

p1=phase(hilbert(y1))，

p2=phase(hilbert(y2))，

p1=p1(floor(end/4)∶floor(3*end/4))，

p2=p2(floor(end/4)∶floor(3*end/4))。

由于瞬时相位两端数据往往不稳定，添加对瞬时相位掐头去尾操作，只保留中间较稳定部分，确保输入变量稳定可靠[13]。然后将2路信号的瞬时相位作为上述基本方法的输入，即可进行时延估计。

采用上述监测环境，使用瞬时相位法估计时延，如图5所示。

图5 亚采样点瞬时相位法时延估计结果(SNR=60 dB)

由图5可见，采用亚采样点瞬时相位法估计的时延为0.000 993 15 s，与实际0.001 s时延非常接近，其估算误差为0.685%，明显优于同条件下的基本方法估算结果，证明瞬时相位法估计的时延准确、有效。

同样，通过降低产生信号信噪比的方式来寻找瞬时相位法可估算时延的信噪比容忍下限。当信噪比降低为30 dB、20 dB时，Delay估算结果分别为0.001 125 8s和0.003 121 1s，估算误差分别为12.58%、212.11%，认为瞬时相位法可估算时延的信噪比容忍下限为20dB，此时2个监测站接收信号也发生严重畸变，仿真结果如图6所示。

图6 亚采样点瞬时相位法时延估计结果

3.2 基本方法与瞬时相位法受噪声影响对比

下面测试了2种方法受噪声的影响程度，在不同信噪比情况下对时延估计的误差进行统计，如表1所示。

表1 2种方法估算误差受信号噪声影响对比

由表1可以发现，瞬时相位法比基本方法对噪声的容限提高了10 dB，在相同噪声情况下时延估计精度也有明显提高，但当信噪比降到20 dB时,这2种方法都失效了。

3.3 基本方法与瞬时相位法算法复杂度

前文分析中可见，瞬时相位法相比基本方法，仅多了求解信号瞬时相位的代码部分，后期用瞬时相位作为算法的输入部分，估算时延代码完全相同，因此二者算法的时间复杂度和空间复杂度相同，都为O(n)。

在联想E40笔记本电脑(CPU:i7-5500U、2.4 GHz)上测试，用Matlab自带tic和toc功能，估算基本方法运行代码所消耗的平均时间为0.145 632 s，瞬时相位法运行代码所消耗的平均时间为0.162 721 s，后者仅慢了0.017 089 s。

4 估计精度与点数的关系

数据试验同时发现信噪比固定时，不断缩小2个信号的时延Delay，估计结果会存在一个下限，换句话说，当时延Delay小到一定程度时，上述时延估计方法也会失效。

程序定义信号采样间隔Ts=0.01，固定y1和y2两路信号的信噪比为60dB，同时固定y1和y2的采样点数为100个点，在不同Delay情况下对时延估计的误差进行统计。

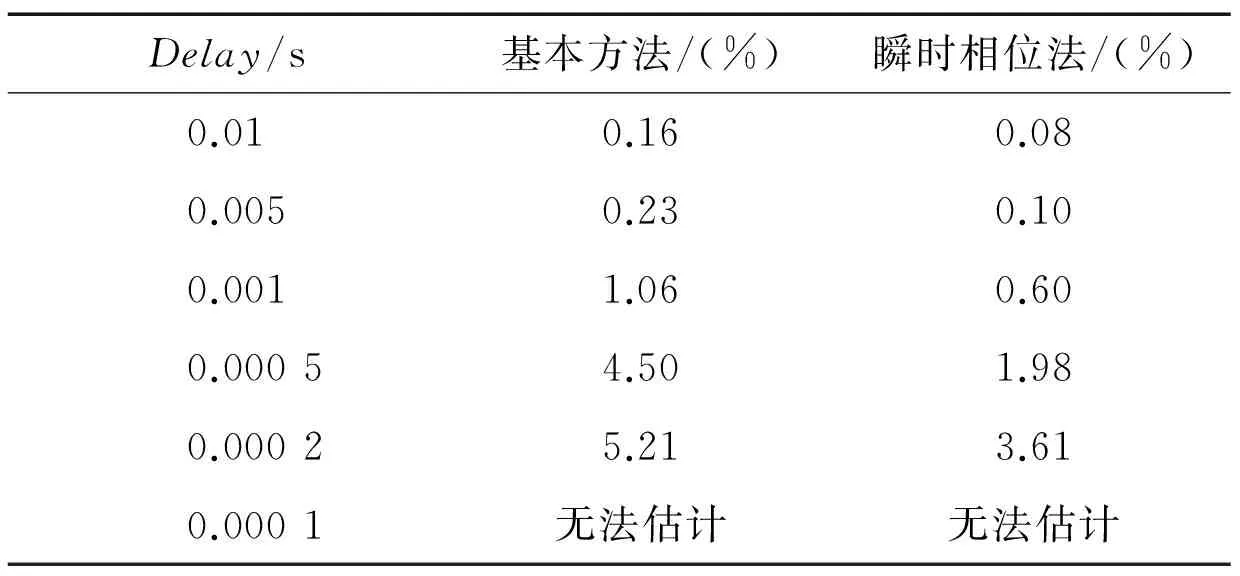
表2 不同Delay下的时延估计误差对比

上述试验结果发现，随着Delay的缩小，2种方法估计误差越来越大，当Delay达到0.000 1时，2种方法同时失效，而0.000 1=0.01/100，正好是Ts和点数N的商。

因此可以大胆假设，如果信号采样间隔为Ts，用N点序列来估计时延，那么能有效估计出的最小时延为：

(4)

仿真试验同时发现如果时延达到Delay_min时就无法估计了。

5 结束语

本文在亚采样点基础上，对两监测站接收无线电信号的时延进行估计，给出算法原理、仿真结果及一般性结论。提出的算法具有实现简单、精度高、算法复杂度低等优势。对于实际布站中，应周全考虑每包信号采集点数与采样率之间的关系。当以250kHz采样率采集输出信号时，采样间隔为Ts=4μs，折算成距离为1 200m，这个精度对TDOA的影响是很大的。在实际TDOA定位中，系统在时间戳的驱动下，每秒采集一包数据，一包数据常包含2 048点IQ数据，如果采用亚采样点时延估计算法，同样在250kHz采样率下，整个系统可估计时延下限可达Delay_min=Ts/N，约为0.002μs，折算成距离差约为0.6m，即使打个折扣，取3倍的Delay_min，那么估计精度也可达到2m，这已经很好的实现了TDOA系统对估算精度的要求，对TDOA时延估计有一定参考价值。

[1] 丁向辉,李 平,孟晓辉.结合信号重心与ASDF估计超声窄带信号时延[J].数据采集与处理,2011.26(6):718-722.

[2] 钟 森,夏 威,何子述.相位噪声对时延估计的影响分析[J].电子与信息学报,2014,36(11):2 614-2 620.

[3] 金中薇,姜明顺,隋青美，等.基于广义互相关时延估计算法的声发射定位技术[J].传感技术学报,2013,26(11):1513-1518.

[4] 张婷菲,赵 昀,王星然.一种GPS多径时延估计的改进粒子滤波算法[J].无线电工程,2014,44(6):21-25.

[5] 张 悦,刘尚合,刘卫东.基于广义互相关与混沌序列预测集成算法的微瞬态电磁辐射信号检测方法[J].电子与信息学报,2015,37(11):2 769-2 775.

[6]GHOLAMIMR,GEZICIS,STROMEG.AConcave-ConvexProcedureforTDOABasedPositioning[J].CommunicationsLetters,IEEE,2013,4(17):765-768.

[7] 王 毅,吴长奇,胡双喜.TDOA中几种时延估计算法的比较[J].无线电通信技术,2008,34(1):52-55.

[8] MEHRPOUYAN H,NSIR A A,BLOSTEIN S D,et al.Joint Estimation of Channel and Oscillator Phase Noise in MIMO Systems[J].IEEE Transactions on Signal Processing,2012,60(9):4 790-4 807.

[9] 史小红.基于TDOA的无线定位方法及其性能分析[J].东南大学学报(自然科学版),2013,43(2):252-257.

[10] 杜彦伸,魏 平,张花国.一种新的基于TDOA与GROA的无源定位算法[J].航空学报,2015,36(9):3 034-3 040.

[11] 李仕云,邓洪权.基于EKF的双站测向/时延联合定位算法[J].无线电通信技术,2015,41(1):38-40

[12] 徐彦凯,双 凯.小波奇异值分解的瞬变弱信号检测[J].中国石油大学学报(自然科学版),2014,38(3):181-185.

[13] 曹轶超,方建安,罗贤云.一个基于TDOA的无线定位新算法[J].电波科学学报,2008,23(5):841-846.

杨建辉 男，(1987—)，硕士，助教。主要研究方向：无源时延定位技术、弱信号检测。

刘玉红 女，(1975—)，硕士，副教授。主要研究方向：数字信号处理、无线传感器网络。

TDOA Time Delay Estimation Based on Sub-sampling Point Level

YANG Jian-hui,WANG Yi-xuan,LIU Yu-hong

(SchoolofElectronic&InformationEngineering,LanzhouJiaotongUniversity,LanzhouGansu730070,China)

The estimation of time delay is greatly influenced by the system sampling rate in passive location.This paper proposes a new time delay estimation algorithm based on sub-sampling points.The method calculates time delay by using the geometrical character of the signal points from two reference stations on the basis of the minimum sampling point.We simulated a signal source and two reference stations in Matlab.In order to prove the validity of the method,baseband signal and instantaneous phase were put into the algorithm for comparing the accuracy of two time delay estimation methods.The result showed that the accuracy of delay algorithm based on sub-sampling is related to signal numbers and sampling period,and at the same sampling rate this method is better than the method with sampling point level.

TDOA;time delay estimation;sub-sampling;instantaneous phase;accuracy analysis

10.3969/j.issn.1003-3106.2017.01.06

杨建辉,王逸轩,刘玉红.基于亚采样点级别的TDOA时延估计[J].无线电工程,2017,47(1):23-26，31.

2016-10-18

甘肃省自然基金资助项目(1506RJZA081)；兰州交通大学校青年基金资助项目(2015009)。

TN98

A

1003-3106(2017)01-0023-04