基于改进的特征提取方法和稀疏表示的单幅图像超分辨率重建算法

王亚辉，贾媛媛，何中市

（重庆大学计算机学院，重庆 400044）

基于改进的特征提取方法和稀疏表示的单幅图像超分辨率重建算法

王亚辉，贾媛媛，何中市

（重庆大学计算机学院，重庆 400044）

为了改善单幅图像的超分辨率重建效果，在基于过完备字典图像的超分辨率重构算法的架构上，应用改进的高斯Laplace算子来提取低频图像的特征，应用于图像重建。该算子主要用于在重建图像的预处理阶段，有效地提取各个方向的边缘特征，既不会造成漏检，也不会加重噪声。实验表明，与现有的几类算法相比较，使用该算子提取特征后，重建图像的效果无论在峰值信噪比还是结相似性都有所提高。

图像的超分辨重建；过完备字典；高斯Laplace

0 引言

图像的超分辨重建是利用一幅或多幅低分辨图像构建出高分辨图像的技术[1]。图像的超分辨重建技术广泛应用于远程监控、军事侦察、医疗图像等领域，有广阔的前景。因此，近三十来，超分辨率重建技术引起了图像处理界的广泛关注。目前主流图像的超分辨率重建方法主要分为三大类。第一类是基于插值[2-3]的方法：主要是通过临近的像素点进行加权来预估插值点的像素，这类算法的复杂度较低，试用于简单的场景，但是在图像的边缘会产生显而易见的伪影；第二类是基于重建[4-7]的方法：这类方法集中探索重建图像的先验知识和约束项，与第一类算法相比，能够得到清晰的图像，但当重建尺度较大时不能得到较好的边缘细节；第三类是基于学习的方法：这类方法的观点主要是估计高分辨率图像（HR，High Resolution）和低分辨率图像（LR，Low Resolution）中图像块之间的映射关系。Freeman[8]等人首先提出了一个马尔科夫随机场模型来学习HR和LR之间的关系，但是需要大量的HR和LR的图像块，算法的复杂度非常高。Dong[9]等人采用卷积神经网络直接对高分辨率图像和低分辨率图像进行端到端的学习。目前研究的主要热点集中于由Yang[10-12]等人在2008年提出的基于稀疏表示的图像的超分辨重建技术。这种技术基于压缩感知理论，假定图像块能够由字典中的少数原子线性表示。根据这种思想，Yang等人提出首先基于训练集合分别学习高、低分辨率过完备字典，然后根据低分辨率过完备字典对LR图像块稀疏表示，最后利用稀疏系数和高分辨过完备字典重建HR图像块。这类方法有较好的自适应性，图像重建效果也令人满意。但字典训练过程中的特征标志搜索算法速度过于缓慢，一般需要三四个小时。Elad[13]等人在Yang的基于稀疏表示的超分辨率重建算法框架上进行了一些有效的改进，字典训练采用了K-SVD[14]（KSingular Value Decomposition）算法，并且运用主成分分析法（PCA，Principal Component Analysis）对图像特征降维，稀疏表示采用OMP[15]（Orthogonal Matching Pursuit）算法。这些方法的使用大量地减少了字典的训练时间，降低了整个算法的时间复杂度，同时提高了重建图像的质量。但是该算法特征提取方法过于简单，没有充分利用图像的先验特征。针对该问题，本文在Elad等人基于稀疏表示图像超分辨重建算法框架上，认真对比了对图像块特征提取的方法，采用了高斯平滑的拉普拉斯算子，更有效地提取边缘高频特征，充分利用图像的先验特征，从而提高了重建图像的质量。

1 基于稀疏表示单幅图像的超分辨重建

高分辨率图像的降质表达式如下（1）所示：

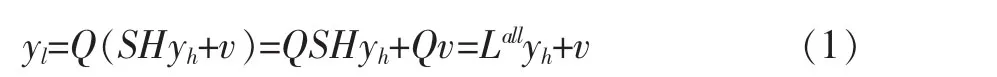
其中，yh，yl∈RNh，H是和S分别是对yh进行低通滤波和向下采样，Q是对低分辨率图像进行插值，使其尺寸大小与高分辨图像的尺寸大小一致，v是高斯噪声，服从v～N（0，σ2I）。

单幅图像的分辨率重建问题可描述为给定一幅低分辨率图像yl，重建成同一场景下较高分辨率图像yh。

单幅图像的超分辨率重建问题可表示为：

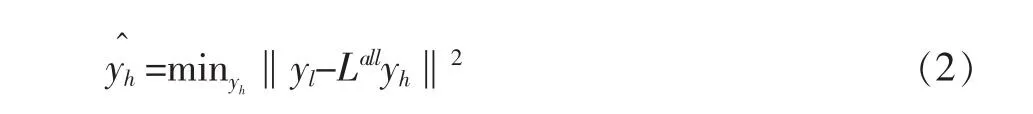
该问题为病态反问题，即不存在唯一解，因此需要引入正则项，将病态反问题转换为适定问题。即：

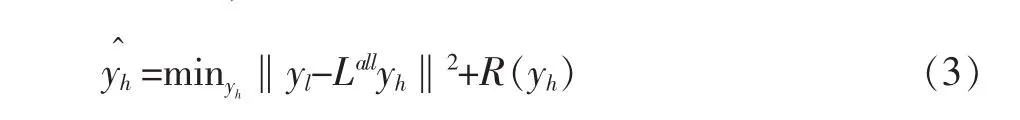
其中R（yh）为正则项，基于稀疏表示的超分辨率重建算法引入图像的稀疏和冗余特征作为正则项，即：

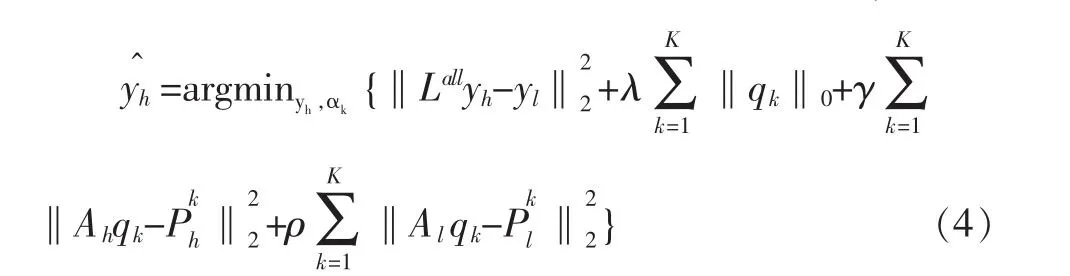
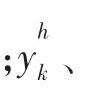
1.1 训练阶段

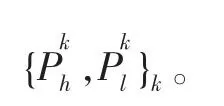
（4）使用K-SVD训练低分辨率图像块的字典Al。

（5）构建与Al相对应的高分辨率图像块的字典Ah。

1.2 重建阶段

（1）给定一个测试的低分辨图像zl，插值得到与目标大小相同的需要重建的低分辨率图像yl，并对yl进行与训练阶段一样的预处理。

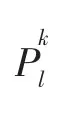
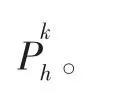
（4）将重建好的高分辨图像块合并成最终的高分辨图像yh。

2 改进的高斯Laplace特征提取

文献[13]对低分辨率图像块进行特征提取，使用的高通滤波器为梯度算子和Laplace算子：

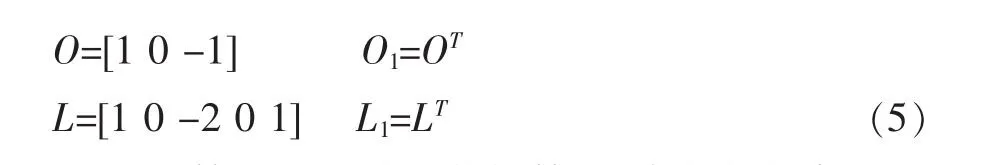
Laplace算子是二阶导数的算子，有很好的各项同性，具有位移不变性和旋转不变性的特点；但丢失了边缘的方向信息，并且加重了噪声。经典的高斯Laplace算子采用高斯滤波和Laplace锐化滤波结合起来，先用高斯平滑噪声，再采用Laplace进行锐化，可以得到优于Laplace的效果。故本文采用了一种改进的高斯Laplace算子用来提取图像的高频特征，再应用于整个图像重建过程中。

文献[16]中提出了一种改进的高斯Laplace算子，如下（6）所示：

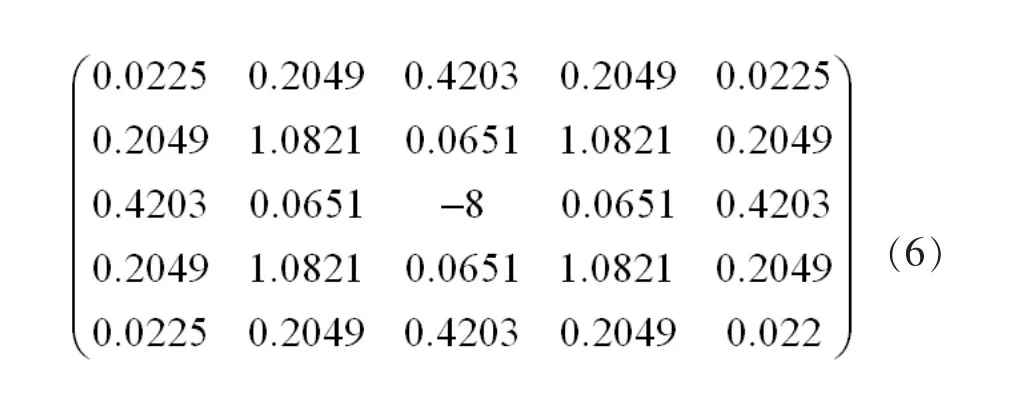
整个Laplace模板[16]在16个方向上都有不同的向量权重，而且不同方向上的权重不同，而同方向权重相等；整个模板没有零点，保证了16个方向都能检测到边缘特征，既不会造成漏检，也不会加重噪声。

3 实验结果

本次实验采用与文献[13]一致的参数，将低分辨率图像重建为3倍大小的高分辨图像，K-SVD的迭代次数为40，训练字典的原子为1000，图像块的大小为[9 9]。将Bicubic插值算法、文献[11]和文献[13]提出的算法和本文采用算法的重建结果进行了对比。主要采用峰值信噪比（PSNR）和结构相似度（SSIM）两个度量标准，其计算方法如公式（7）（8）所示

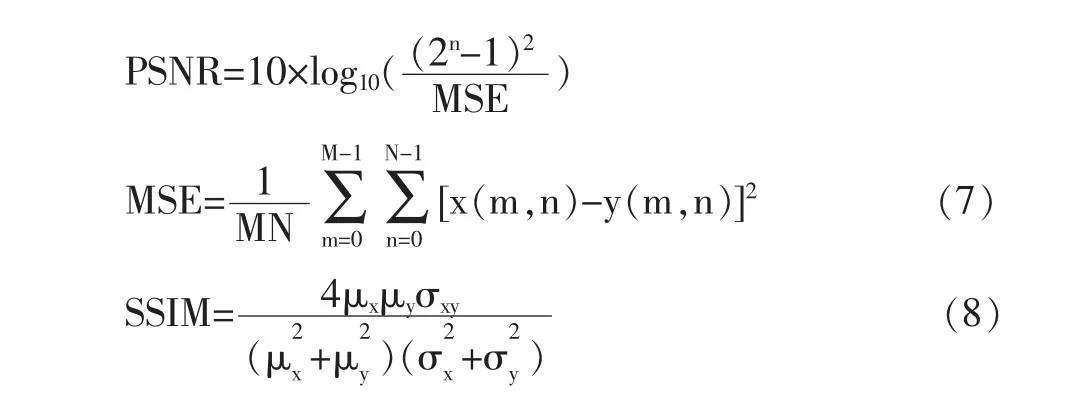
其中，M和N代表x和y的维数，μx和μy是均值，σx和σy代表方差，σxy代表x和y之间的协方差。PSNR的值越高，SSIM越接近于1，代表重建效果越好。

图1展示了图像Comics四种方法重建结果。从图一中可以看出，使用插值方法处理的图像比较平滑，导致图像模糊，边缘锯齿明显，伪影严重。与文献[11]和文献[13]方法对比，本文的方法在脸部边缘的轮廓的清晰度度上略胜一筹，从Comics图像的右边脖子中可以看出，边缘清晰，颜色较统一，均匀，较少出现伪影。

表1和表2分别是用四种方法对10幅图像进行重建结果的PSNR和SSIM值展示，可以看出，应用本文方法重建的图像，优于其他三种方法的PSNR和SSIM值。例如Comics图像的重建效果，PSNR结果是Bicubic的最差，为23.3，文献[11]和文献[13]比Bicubic要显著好的多，分别是23.9和24.0，本文的方法是24.2。对于SSIM结果的对比依旧是Bicubic方法最差，为0.691，文献[11]和文献[13]和本文的方法对比结果递增，分别为0.747、0.750和0.753。

图1 图片Comics四种方法重建的结果

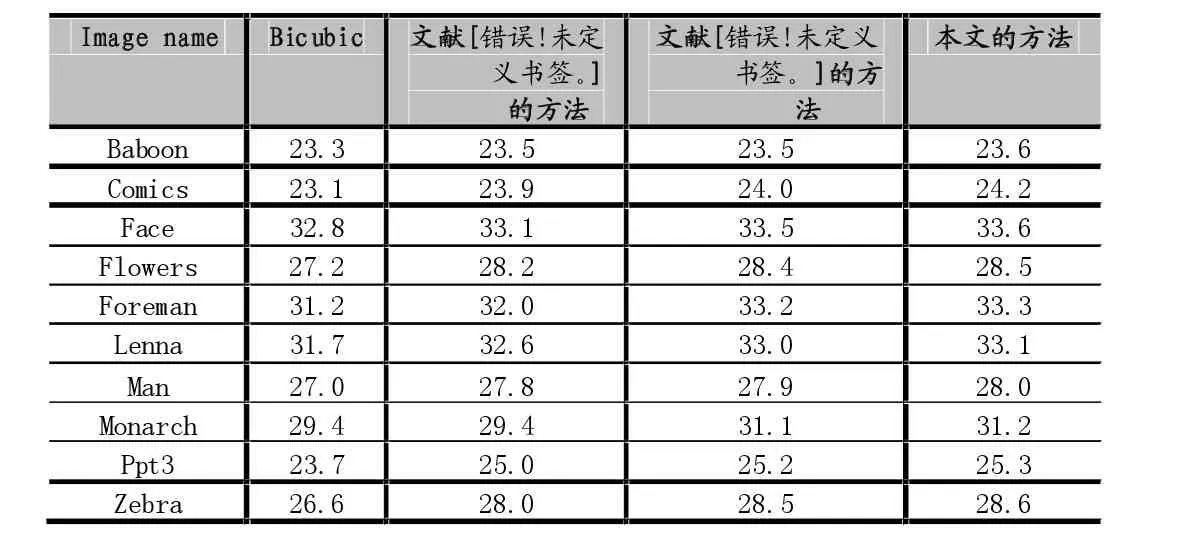
表1 四种方法对10幅图像重建结果的PSNR

表2 四种方法对10幅图像重建结果的SSIM

4 结语

本文在基于稀疏表示的图像超分辨重建算法的框架上，采用了高斯Laplace算子对图像提取高频特征，用于图像重建。实验结果表明，无论是从感官上还是从实现数据的统计上表明，本文方法都是要优于传统的插值算法，以及文献[11]和文献[13]两种基于稀疏表示的SR算法，同时也证明了本文的改进是有效的。

[1]沈焕锋，李平湘，张良培，等.图像超分辨率重建技术与方法综述[J].光学技术，2009，35（2）：194-199.

[2]Hou H，Andrews H.Cubic Splines for Image Interpolation and Digital Filtering[J].IEEE Transactions on Acoustics，Speech，and Signal Processing，1978，26（6）:508-517.

[3]Keys R.Cubic Convolution Interpolation for Digital Image Processing[J].IEEE Transactions on Acoustics，Speech，and Signal Processing，1981，29（6）:1153-1160.

[4]Stark H，Oskoui P.High-Resolution Image Recovery from Image-Plane Arrays，Using Convex Projections[J].JOSA A，1989，6（11）: 1715-1726.

[5]Irani M，Peleg S.Improving Resolution by Image Registration[J].CVGIP:Graphical Models and Image Processing，1991，53（3）:231-239.

[6]A.Gholipour，J.A.Estroff，S.K.Warfield.Robust Super-Resolution Volume Reconstruction from Slice Acquisitions:Application to Fetal Brain MRI[J].IEEE Transactions on Medical Imaging，2010，29（10）:1739-1758.

[7]K.Jafari-Khouzani.MRI Upsampling Using Feature-Based Nonlocal Means Approach[J].IEEE Transactions on Medical Imaging，2014，33（10）:1969-1985.

[8]Freeman W T，Jones T R，Pasztor E C.Example-Based Super-Resolution[J].IEEE Computer Graphics and Applications，2002，22（2）:56-65.

[9]Chao Dong，Chen Change Loy，Xiaoou Tang.Image Super-Resolution Using Deep Convolutional Networks.IEEE Transactions on Pattern Analysis and Machine Intelligence，38（2）:295-307，Feb.2016.

[10]Yang J，Wright J，Huang T，et al.Image Super-Resolution as Sparse Representation of Raw Image Patches[C].Computer Vision and Pattern Recognition，2008.CVPR 2008.IEEE Conference on.IEEE，2008:1-8.

[11]Yang J，Wright J，Huang T，et al．Image Super-Resolution Via Sparse Representation[J].IEEE Transactions on Image Processing，2010，19（11）:2861-2873．

[12]Yuanyuan Jia，Zhongshi He，Ali Gholipour，Simon K.Warfield（2015）Single Anisotropic 3D MR image Upsampling via Over-Complete Dictionary Trained from In-plane High Resolution Slices[J].IEEE journal of biomedical and Health Informatics.（Publish online）

[13]Zeyde R，Elad M，Protter M.On Single Image Scale-up Using Sparse-Representations［DB］.Curves and Surfaces，Springer，2012．

[14]Elad M，Aharon M，Bruckstein A M.The K-SVD:an Algorithm for Designing of Overcomplete Dictionaries for Sparse Representations [J].IEEE Trans.Image Process，2006，15（12）:3736-3745.

[15]Pati Y C，Rezaiifar R，Krishnaprasad P S.Orthogonal Matching Pursuit:Recursive Function Approximation with Applications to Wavelet Decomposition[C].Signals，Systems and Computers，1993.1993 Conference Record of The Twenty-Seventh Asilomar Conference on.IEEE，1993:40-44.

[16]剑玲，邹辉.基于高斯Laplace算子图像边缘检测的改进[J].微电子学与计算机，2007，24（9）:155-157.

Single Image Super-Resolution Reconstruction Algorithm Based on Improved Feature Extraction and Sparse Representation

WANG Ya-hui，JIA Yuan-yuan，HE Zhong-shi

（College of Computer Science,Chongqing University,Chongqing 400044）

In order to improve the super-resolution reconstruction effect of single image,uses an improved Gaussian Laplace operator to extract the features of low-frequency on image for the image super-resolution reconstruction algorithm based on over-complete dictionary.This operator is mainly used to extract the edge features of each direction effectively during the preprocessing phase of the reconstructed image, which will not result in missed detection and no increase of noise.Experiments show that,compared with the existing algorithms,the effect of reconstructing the image using the operator is improved both in the PSNR and the SSIM.

Super-Resolution Reconstruction of Image;Over-Complete Dictionary;Gaussian Laplace;Timer

1007-1423（2017）02-0063-05

10.3969/j.issn.1007-1423.2017.02.016

王亚辉（1992-），男，湖南益阳人，硕士，研究方向为数字图像处理

2016-11-01

2017-01-05

贾媛媛，教师，研究方向为医学图像处理

何中市，教授，博士生导师，研究方向为模式识别、机器学习与数据挖掘、自然语言、处理与数字图像处理