梯度神经网络在求解矩阵平方根中的应用

严慧玲，肖 林，周文辉

(1.吉首大学 数学与统计学院，湖南 吉首 416000; 2.吉首大学 信息科学与工程学院，湖南 吉首 416000)

梯度神经网络在求解矩阵平方根中的应用

严慧玲1，肖 林2，周文辉2

(1.吉首大学 数学与统计学院，湖南 吉首 416000; 2.吉首大学 信息科学与工程学院，湖南 吉首 416000)

矩阵的平方根问题是关于求解矩阵问题的一种特殊情况，在科学与工程领域中应用是极其广泛的。不同于用数值方法求解，采用梯度神经网络对矩阵平方根问题进行求解。为了求解一般矩阵的平方根，定义了一个基于范数的标量取值的能量函数，然后根据梯度下降法，设计了一个演化公式，从而推导出了求解矩阵平方根的梯度神经网络模型。借助MATLAB进行计算机模拟仿真，仿真结果证实了梯度神经网络在求解矩阵平方根的可行性和有效性。而且，通过选取不同的设计参数取值，可以大大加快梯度神经网络求解矩阵平方根的收敛速度。结果说明，设计参数的取值在梯度神经网络求解矩阵平方根当中有着至关重要的作用。

梯度神经网络；梯度下降法；矩阵平方根；MATLAB仿真

0 引 言

神经网络包括两个主要方面,即人工神经网络(Artificial Neural Network,ANN)和由真正的生物神经元组成的网络(Biological Neural Network,BNN)[1]。人工神经网络由神经元模型构成,这种由许多神经元组成的信息处理网络具有并行分布结构。每个神经元具有单一输出,并且能够与其他神经元连接;存在许多(多重)输出连接方法,每种连接方法对应一个权系数[2]。人工神经网络是由大量简单的处理单元组成的非线性、自适应、自组织系统，是在现代神经科学研究成果的基础上，试图通过模拟人类神经系统对信息进行加工、记忆和处理的方式，设计出的一种具有人脑风格的信息处理系统[3-4]。当前，神经网络已经成为许多学科十分青睐的研究话题。

梯度下降法也叫最优下降法，是一种最优化算法，顾名思义，就是在计算过程中使目标函数沿梯度下降速度最快或上升最快的方向进行。最速下降法以负梯度方向为搜索方向，其越接近目标值，步长越小，前进越慢[4]。

矩阵是高等代数学中的常用工具，也常见于统计分析等应用数学学科中。在物理学中，矩阵在电路学、力学、光学和量子物理学中都有应用，在计算机科学、三维制作等领域也频繁使用。顾传青等提出了改进的方法来计算矩阵A的平方根,也就是应用一些牛顿法的变形来解决二次矩阵方程。研究表明,改进的方法比牛顿算法和一些已有的牛顿算法的变形效果要好[5]。黄德超利用矩阵分块逐次降阶的方法,给出了一种快速算法,用来计算r循环矩阵的同型平方根矩阵(平方根矩阵也为r循环矩阵)[6]。杨雁等讨论了布尔矩阵平方根问题及其与图着色问题的关系，得到了有平方根的布尔矩阵具有的一些性质[7]。Stewart等研究表明，运用矩阵平方根算法实现的卡尔曼滤波器比不要求矩阵平方根的算法相对要快，也相对稳定[8]。关于矩阵平方根的研究以及算法在各行各业的应用，这里主要介绍怎样运用梯度下降法求解矩阵的平方根。假若给定一个矩阵A,有X2-A=0成立，则称X为矩阵A的平方根。文中主要借助Matlab软件和梯度神经下降法求解矩阵平方根[9-14]。

设计了一个能量函数，利用梯度神经的方法，结合MATLAB仿真软件进行建模、仿真并加以验证。给出不同参数，观察函数的收敛速度。最后，通过对MATLAB得到的数据进行分析，肯定了该神经网络在求解矩阵平方根中的可行性和准确性。

1 梯度神经网络设计

1.1 问题描述

首先，对于i行i列的矩阵可以用A∈Ri×i表示。通常，任何的矩阵方程求解都应该有一个等式成立。为了不失一般性，设置一个一般的求解矩阵方程的方程式。

先考虑下面这个一般的等式问题：

X2(t)-A=0

(1)

其中，A就是要求解的矩阵X(t)的平方。

文中就是要找到一个确定的X(t)，使得方程(1)在t>0都能成立。因此，主要对式(1)进行研究，设计出一个梯度神经网络：这个梯度神经网络可以求解任何时域X(t)∈R问题的解。

1.2 梯度神经网络模型

关于阅读理念，《小学语文课程标准》中指出，教师在阅读教学中使学生获得一定的情感体验，即要求教师应引导学生有感情地阅读课文内容。在阅读中，教师不应把自己的思维方式强加给学生，限制住学生的想象力，而应该让学生自由发挥想象，对课文的内容形成独特的理解和感悟。另外，应教导学生注重积累，培养学生对语言文字的感知能力。并将多种阅读方法教给学生，让学生使用探究性的阅读方式进行阅读，摒弃接受型阅读方式，增强学生独立阅读的欲望。就本人的教学经验，我归纳了一下几点策略：

根据神经网络思维的设计方法，推理出具有一般性的梯度神经网络模型来解决像式(1)的问题，具体的设计流程如下：

(1)为了求解矩阵A的解，即求出方程(1)的解，可以自定义一个基于范数的标准取值的能量函数ε(X)，用于监控式(1)的求解过程：

ε(X)=‖X2(t)-A‖/2

(2)

很明显，求解的问题是要方程(1)成立，故当方程(2)等于零时，相对应的X就是所要求的理论解。那么，只要求出能量函数ε(X)=0时对应的X就行了。

(2)为了使能量函数(2)能够收敛到零，应用梯度下降法的思想，可以使它沿着负梯度方向下降，于是对其求导：

(3)

(3)基于梯度神经网络设计方法，根据负梯度方向，可以得到如下的求解矩阵平方根的梯度神经网络模型：

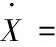
(4)

其中，设计参数λ>0，为自定义设计，主要作用是调节模型(4)的收敛速度；函数X(t)从初始值X(0)出发，对应于一般等式方程(1)的解。

2 计算机仿真验证

该小节将挑选几个不同阶次的矩阵进行验证。

例1：3阶矩阵的平方根。

这里，取A=[6 -0.75 6.5;-7 5.25 -15.5;4 -3 11]，λ取20，得到的图形如图1和图2所示。

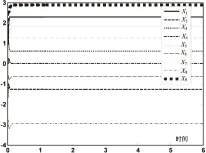
图1 梯度神经网络的状态解(1)

由图形可以看出，X(t)的取值随着时间的增加，比较快地收敛到了一个定值，这个定值就是想要的X(t)的值。同时，从能量函数图可以看出，能量函数在0.5s左右收敛到了0，这里λ的取值为20，如果λ取值更大些，收敛效果会更理想。

图2 λ=20的能量函数收敛情况

在保证其他条件不变的情况下把λ的取值设为70，再来观察其收敛性，如图3和图4所示。

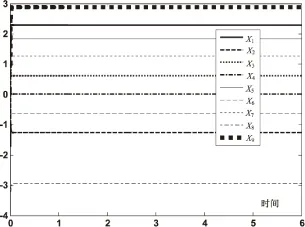
图3 梯度神经网络的状态解(2)

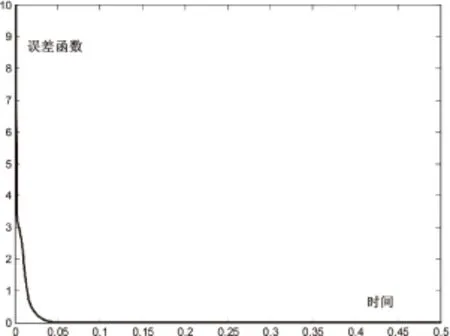
图4 λ=70的能量函数收敛情况

可以清楚地看出，当λ=70时，即随着λ的增大，能量函数收敛到0的时间缩短到0.2s以内，由此可见λ取值对能量函数收敛速度的重要性。

例2：下面计算一下2阶矩阵的平方根，这里取A=[5 2;6 8],λ=5,得到的图形如图5和图6所示。

很显然，无法手动计算该2阶矩阵的平方根的理论解。图6显示了梯度神经网络求解该2阶矩阵的平方根的能量函数收敛情况。可以从中看到,λ=5时误差函数在1s内就能收敛到零,同样也说明了梯度神经网络的有效性。而且,也给出了该能量函数所对应的状态解，在[0,3]区域内的神经状态解都收敛到某一特定值。这一仿真实例再次说明了提出的梯度神经网络的正确性和实用性。

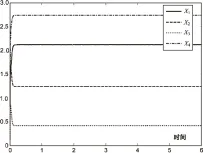
图5 梯度神经网络的状态解(3)

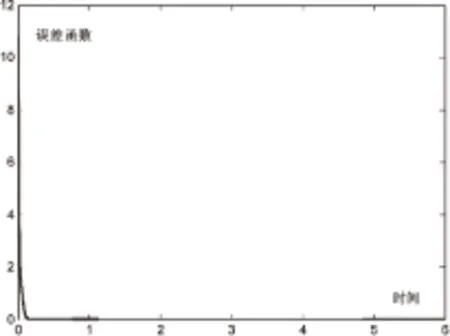
图6 λ=5的能量函数收敛情况

3 结束语

为了求解矩阵平方根，定义了一个基于平方的标量取值的能量函数，并且基于该能量函数设计了一个演化公式，由此得到求解矩阵平方根的梯度神经网络模型。借助Matlab软件进行了计算机仿真模拟，仿真结果证实了梯度神经网络的有效性。并且可以通过设置不同的λ的值，来调节能量函数的收敛速度。

[1] 陈惟昌.生物神经元网络与人工神经网络[J].科技导报,1991(3):41-44.

[2] 汤素丽,罗宇锋.人工神经网络技术的发展与应用[J].电脑开发与应用,2009,22(10):59-61.

[3] 蒋宗礼.人工神经网络导论[M].北京:高等教育出版社，2001：10-13.

[4] 陈海波,吕咸青,乔彦松.梯度下降法在沉积物粒度分布拟合中的应用[J].数学的实践与认识,2011,41(13):78-87.

[5] 顾传青,刘 强.一类变形的牛顿法求解矩阵平方根(英文)[J].应用数学与计算数学学报,2012,26(2):136-142.

[6] 黄德超.2k阶r-循环矩阵开平方的快速算法[J].杭州师范学院学报:自然科学版,2004,3(1):17-21.

[7] 杨 雁,贾堰林,王学平.布尔矩阵平方根问题及其与图着色问题的关系[J].高校应用数学学报,2013,28(2):222-228.

[8] Larin V B,Aliev F A.Construction of square root factor for solution of the Lyapunov matrix equation[J].Systems & Control Letters,1993,20(2):109-112.

[9] 张雨浓,张禹珩,陈 轲,等.线性矩阵方程的梯度法神经网络求解及其仿真验证[J].中山大学学报:自然科学版,2008,47(3):26-32.

[10] Xiao L,Zhang Y.Two new types of Zhang neural networks solving systems of time-varying nonlinear inequalities[J].IEEE Transactions on Circuits Systems I Regular Papers,2012,59(10):2363-2373.

[11] Xiao L,Zhang Y.From different Zhang functions to various ZNN models accelerated to finite-time convergence for time-varying linear matrix equation[J].Neural Processing Letters,2014,39(3):309-326.

[12] Xiao L.A finite-time convergent neural dynamics for online solution of time-varying linear complex matrix equation[J].Neurocomputing,2015,167:254-259.

[13] Xiao L.A nonlinearly-activated neurodynamic model and its finite-time solution to equality-constrained quadratic optimization with nonstationary coefficients[J].Applied Soft Computing,2016,40:252-259.

[14] Xiao L,Lu R.Finite-time solution to nonlinear equation using recurrent neural dynamics with a specially-constructed activation function[J].Neurocomputing,2015,151:246-251.

Application of Gradient Neural Network in Matrix Square Root Solving

YAN Hui-ling1,XIAO Lin2,ZHOU Wen-hui2

(1.College of Mathematics and Statistic,Jishou University,Jishou 416000,China; 2.College of Information Science and Engineering,Jishou University,Jishou 416000,China)

Matrix square root problem can be regarded as a special case of matrix problems,and has a wide application in scientific and engineering fields.Different from the conventional numerical methods,the gradient neural network is adopted to solve matrix square root problem.In order to solve the square root of a matrix,a norm-based scalar-valued energy function is defined.Then,according to the gradient descent method,an evolution formula is designed.Thus,the gradient neural network is derived for finding the square root of a matrix by expanding the evolution formula.With the aid of computer simulation based on MATLAB,the simulation results confirm the accuracy and validity of the gradient neural network for finding matrix square root.Furthermore,by choosing different values of the design parameter,the convergence speed of the gradient neural network for matrix square root solving has been improved greatly.The results show that design parameter plays an important role in the gradient neural network for solving matrix square root.

gradient neural network;gradient descent method;matrix square root;MATLAB simulation

2015-12-07

2016-04-20

时间：2017-01-10

国家自然科学基金资助项目(61503152)；湖南省自然科学基金(2016JJ2101)；湖南省教育厅优秀青年项目(15B192)；吉首大学2015年实验教学改革研究项目(2015SYJG034)；吉首大学2016年研究生科研创新项目(JGY201643)；吉首大学2016年校级课题(Jdy2016009)；吉首大学2016年大学生研究性学习和创新性实验计划项目资助(教通[2016]13号)

严慧玲(1995-)，女，研究方向为神经网络；肖 林，讲师，博士，通讯作者，从事信息类课程教学和人工神经网络方面的科学研究工作。

http://www.cnki.net/kcms/detail/61.1450.TP.20170110.0941.008.html

TP39

A

1673-629X(2017)02-0155-03

10.3969/j.issn.1673-629X.2017.02.035