大规模MIMO双向中继系统的功率分配

李晓婷

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

大规模MIMO双向中继系统的功率分配

李晓婷

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

在中继的发送端和接收端安装大量天线，可以大大地提高系统性能。提出一种大规模MIMO双向中继架构。在每个相干时间间隔内，信息交换发生在三个阶段：训练阶段、多址阶段、广播阶段。在训练阶段，中继通过正交导频序列对所有用户进行独立的信道估计。假设中继已知不完全信道状态信息情况下，设计一个最小均方差(MMSE)滤波器减轻环回干扰，采用迫零(ZF)滤波器进行检测和预编码处理。通过评估此系统中继和目的点的误码率(BER)，选出最佳的中继发送功率，并且提出了一种最佳功率分配算法。在满足通信对速率约束条件的情况下，此算法可以算出中继最小发送功率。仿真结果表明，当MMSE滤波器和最佳功率分配算法都被采用的时候，系统将获得更高的能源效率。

双向中继；MIMO；信道估计；MMSE；迫零；功率分配

0 引 言

目前，随着移动通信技术的快速发展、移动通信网络的广泛使用以及移动通信用户数量的迅猛增长，在移动通信网络中实现双向中继技术，已成为移动通信系统发展的热点之一[1-3]。无线双向中继网络中端到端系统性能取决于时隙和功率的联合分配,以及在非对称信道下经过资源优化分配后,在中继节点上采用何种AF/DF/CF机制[4]。文献[5]描述了多用户采用AF转发中继的比例公平调度。在多用户情况下，考虑子载波配对的问题，并且阐述了OFDMA中继网络中的GPF调度帧问题。文献[6]重点研究了共享中继网络的调度和资源分配方面的问题。描述了一个共享中继架构，以减少无线蜂窝网络小区间干扰。共享中继架构就是具有多个天线的单个中继被放置在小区的边缘，并且由多个扇区共享。文献[7]详述了中继选择和资源分配的联合优化，根据数据速率要求来最小化系统的发射功率消耗，提高能源效率。

现在大多数的无线双向中继的理论研究仍然局限于两源节点和单中继、多源节点和单中继的系统模型[8-10]。这种研究模型已经不能满足日益复杂的网络环境要求。对于大规模MIMO和双向中继系统相结合的模型来说,目前对其的研究国际上刚处于起步阶段,只有少数文章可参考。文献[11]详述了大规模天线阵列的双向中继网络采用导频序列，进行信道估计的两种方案。文献[12]研究了MIMO双向中继网络中源和中继的天线选择问题，提出两个相似的最优算法：JRSAS和SRSAS。这两种算法都可以接近最佳穷举搜索(ES)算法，而且显著减少了计算复杂度。

下一代网络的基本思想是基站通过使用大量的天线，可以服务于更多的用户和设备。此研究涉及到各种信号处理技术，如信道建模和估计，预编码和检测算法。文中提出一种大规模MIMO双向中继架构，所有用户都具有一个独立的天线，而中继节点配备一个非常大的天线阵列。信息交换发生在三个阶段：训练阶段、多址阶段、广播阶段。通过在训练阶段的导频序列使中继对所有用户进行独立的信道估计。采用迫零ZF滤波器进行检测、预编码，线性处理抑制环回干扰。提出一种最佳功率分配算法，减小了发送功率，降低了误码率，提高了能源利用率和系统的整体性能。

1 系统模型

MIMO双向中继系统如图1所示。

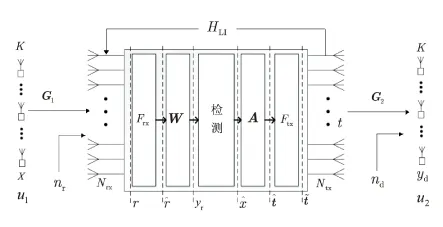
图1 MIMO双向中继系统

考虑两组用户u1、u2，每组包含K个单线用户，中继含有Nrx根接收天线和Ntx根发送天线(K≪Nrx,Ntx)。x的第k个用户和y的第k个用户只通过中继相互传输信息。

1.1 信道估计

向量X是源点到中继发送的符号，向量t是中继到目的点发送的波束成形符号，假定这些向量是取自一个M-QAM星座且输出信号是规范的、不相关的。因此，每个源点的发送功率独立于K，中继的总发送功率独立于Ntx。中继和目的点接收的符号向量分别是：

(1)

(2)

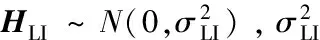
由于源点到中继和中继到目的点的符号传输都经过一个MIMO信道，所以

(3)

其中，D1、D2是一个对角矩阵，服从对数正态分布，表示大规模信道的影响;H1、H2服从标准正态分布,表示快衰落信道。

为了有效地应用检测，预编码和干扰消除技术，必须进行信道估计。中继通过采用训练阶段的导频序列对所有用户进行独立的信道估计，然后使用迫零ZF滤波器处理接收信号。假设所有通信链路共享同一时频资源，采用TDD传输模式。在一个相干时间间隔内，信息交换发生在三个阶段：训练阶段、多址阶段、广播阶段，如图2所示。

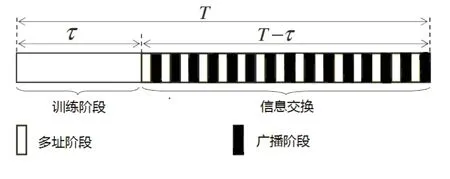
图2 三个阶段

在训练阶段，每个用户分配一个τ长度的导频序列，所有用户同时发送导频序列到中继，所以中继接收的导频矩阵为：

(3)

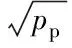
中继根据用户发送的导频矩阵进行信道估计，用于信号处理。

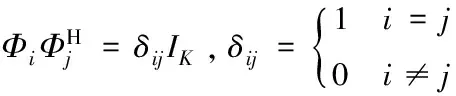
(4)

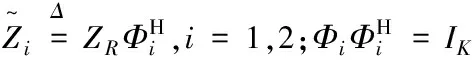
1.2 检测和预编码

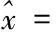
(5)

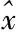
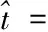
(6)

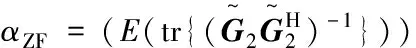
1.3 环回干扰(Loopback Interference,LI)

(7)

若Ftx固定，则

(8)

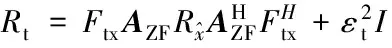
由式(7)所提供的解决方案对应于文献[13]中的零空间投影，但是一般找到针对大规模阵列的解决方案是困难的。与此相反，式(8)是一个封闭的表达式，包含信道估计、发送向量的协方差矩阵和噪声。根据所考虑的模型，给定一组参数，可以预测端到端的误码率：若中继具有较低的发送功率pR，会降低环回干扰功率、减少估计误差的影响和射频损伤；若中继具有较高的发送功率pR，会提高信噪比(SNR)，降低误码率(BER)。因此，当固定源点的发送功率时，若使得端到端的BER最小，pR的选择很重要。

2 功率分配

中继受到的干扰主要取决于它的发送功率，并且直接影响了端到端的性能。因此，找到满足系统要求的最佳功率很重要。

考虑每个链路的可达速率，文献[14]中提到源点和目的点之间的发送链路速率：

Rk=min{R1,k,R2,k}

(9)

其中，R1,k表示源点和中继之间的可达速率；R2,k表示中继和目的点之间的可达速率。

检测前，中继接收的信号为：

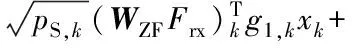
(10)

其中，g1,k表示G1的第k列。

检测前，目的点接收的信号为：

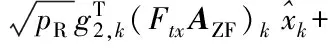
(11)

以上两式均可看作是期望的信号加上不相关的等效噪声(信道衰落、通信对之间的干扰、环回干扰、高斯噪声)。

文中的目的是在保证达到每个通信对期望速率的条件下，计算最优的源点和中继的发送功率。另外，还要满足峰值功率约束，考虑整体功耗。也就是说，既要保证系统的能源效率最大，又要保证总功率最小：

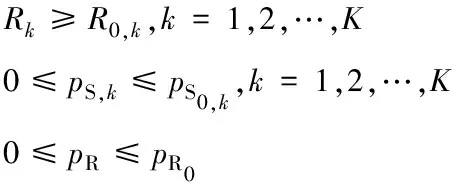
(12)

其中，R0,k表示通信对k要求达到的速率；pS0,k表示通信对k要求达到的峰值功率；pR0表示中继的峰值功率。

为了取得源和中继的最佳功率，提出一个简单有效的基于线性规划的迭代算法。

步骤1：第一次迭代i=1，L是迭代次数上限，Nit是每次迭代信道实现的数目。系统要求源点和中继达到的峰值功率为:

pS,k,1=pS0,k，pR,1=pR0

步骤2：计算Nit个信道的统计信息。首先，生成信道矩阵G1,G2，LI信道矩阵HLI，ZF滤波器的传输矩阵和预编码矩阵WZF,AZF；然后，联合pS,k,i,pR,i计算前置滤波器Frx；最后，计算所有通信对的可达速率R1,k和R2,k。在大规模MIMO系统中常用中心极限定理近似等效噪声项为高斯噪声项[15]，因此R1,k和R2,k的近似值是：

R1,k=log2(1+

(13)

(14)

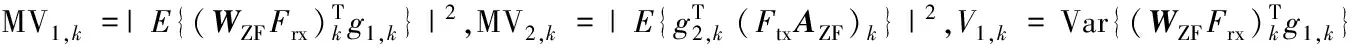
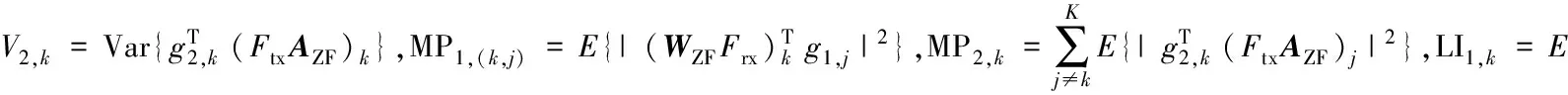
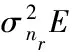
获取信道统计信息的平均值，解决系统能源效率最大且源点和中继总功率最小的问题(见式(12))，得出新的pS,k,i,pR,i。

步骤3：给源点和中继的峰值功率重新赋值(见式(15))，进行再一次迭代，直到i=L结束。

pS,k,i+1=pS,k,i,pR,i+1=pR,i,i=i+1〗

(15)

3 系统仿真分析

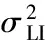
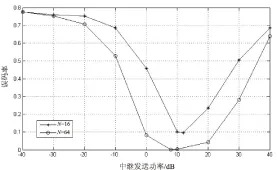
图3 端到端的BER

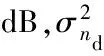
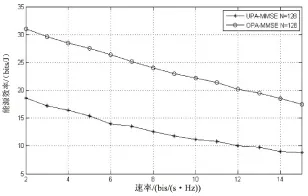
图4 系统能源效率

4 结束语

文中提出一种大规模MIMO双向中继架构，所有用户都具有一个独立的天线，而中继节点配备有一个非常大的天线阵列。中继采用两个滤波器：ZF滤波器进行检测和预编码处理；MMSE滤波器抑制环回干扰。通过对端到端BER的分析，可以选择一个最佳的中继功率分配。与平均功率分配算法进行比较，该算法显著提高了能源效率。

[1] 林文佳,叶 伟,杨 馨.蜂窝通信中中继双向传输技术[J].计算机工程与设计,2010,31(17):3800-3802.

[2] 杨 波,于宏毅,吕 凌,等.高频谱效率的双向连续中继技术[J].北京邮电大学学报,2009,32(1):10-13.

[3] 刘 通,陈前斌,唐 伦,等.Two-way中继系统中的双向中继选择及功率分配策略[J].计算机应用研究,2010,27(7):2697-2699.

[4] 万庆涛,马冠一.中继系统中断概率研究[J].计算机工程与应用,2013,49(11):24-26.

[5]SharifianA,DjukicP,YanikomerogluH,etal.Generalizedproportionallyfairschedulingformulti-useramplify-and-forwardrelaynetworks[C]//Vehiculartechnologyconference.Ottawa,Canada:IEEE,2010:1-5.

[6]LinYicheng,YuWei.Fairschedulingandresourceallocationforwirelesscellularnetworkwithsharedrelays[J].IEEEJournalonSelectedAreasinCommunications,2012,30(8):1530-1540.

[7]ChenYu,FangXuming,HuangBo.Energy-efficientrelayselectionandresourceallocationinnonregenerativerelayOFDMAsystems[J].IEEETransactionsonVehicularTechnology,2014,63(8):3689-3699.

[8] 郑 毅,李中年,王亚峰,等.LTE-A系统中继技术的研究[J].现代电信科技,2009,39(6):45-49.

[9] 赵欣丽.LTE-Advanced系统中继技术综述[J].电子质量,2010(9):42-44.

[10] 张志恒.LTE-Advanced系统中继技术的研究[J].信息通信,2014(3):188-190.

[11] Ngo H Q,Larsson E G.Spectral efficiency of the multipair two-way relay channel with massive arrays[C]//Proceedings of ACSSC.[s.l.]:IEEE,2013:275-279.

[12] Yu Yuehua,Wang Peng,Li Yonghui,et al.Computationally efficient relay-source antenna selection for MIMO two-way relay networks[C]//2015 IEEE ICC.[s.l.]:IEEE,2015:1625-1630.

[13] Riihonen T,Werner S,Wichman R.Mitigation of loopback self-interference in full-duplex MIMO relays[J].IEEE Transactions on Signal Processing,2011,59(12):5983-5993.

[14] Liu Yinjun,Yan Shi,Li Xiangling,et al.Energy-efficient resource allocation for multi-user two-way relay-assisted OFDM system[C]//21st international conference on telecommunications.[s.l.]:[s.n.],2014:150-154.

[15] Hassibi B,Hochwald B M.How much training is needed in multiple antenna wireless links?[J].IEEE Transactions on Information Theory,2003,49(4):951-963.

Power Allocation of Massive MIMO Two-way Relay System

LI Xiao-ting

(College of Telecommunications & Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

The system performance can be greatly increased when the relay is equipped with a large number of antennas on both transmitter and receiver.A massive MIMO two-way relaying architecture is presented.Within each coherence interval,the information exchange occurs in three phases including the training phase,the multiple-access phase,and the broadcast phase.In the training phase,the relay estimates the channels based on pilots transmitted from the users and the pilot sequences assigned for all users in both groups are pairwisely orthogonal.It assumes the relay knows imperfect channel state information and designs a Minimum Mean-Square Error (MMSE) filter to reduce the interference.Then,Zero-Forcing (ZF) filters is adopted for both detection and precoding.The system performance is evaluated in terms of Bit Error Rate (BER) at both relay and destinations.An optimal power allocation algorithm is put forward that computes the minimum power that satisfies the rate constraints of each pair.Simulation results show that when both MMSE filtering and optimal power allocation algorithm are used,the system achieves higher energy efficiency.

two-way relay;MIMO;channel estimation;MMSE;zero-forcing;power allocation

2016-04-06

2016-08-10

时间：2017-01-10

国家自然科学基金资助项目(61372125，61401234)

李晓婷(1990-)，女，硕士研究生，研究方向为下一代通信网络技术。

http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1019.054.html

TP302

A

1673-629X(2017)02-0143-04

10.3969/j.issn.1673-629X.2017.02.032