基于新型鲁棒字典学习的视频帧稀疏表示

钱 阳，李 雷

(南京邮电大学 视觉认知计算与应用研究中心，江苏 南京 210023)

基于新型鲁棒字典学习的视频帧稀疏表示

钱 阳，李 雷

(南京邮电大学 视觉认知计算与应用研究中心，江苏 南京 210023)

字典学习方法是一种非常有效的信号稀疏表示方法，在稀疏信号处理领域应用极其广泛。然而，实际应用中，训练样本和测试样本可能会受到损坏并且含有噪声和异常值，这将严重影响字典学习方法的性能。为此，不同于传统的字典学习方法从干净数据中学习字典，提出一种新型鲁棒字典学习算法，旨在处理训练样本中的异常值。该算法通过采用交替近端线性化方法求解非凸的最小l0范数，在学习鲁棒字典的同时隔离训练样本中的异常值。大量仿真对比实验表明，所提算法具有更好的鲁棒性，并能提供很好的性能改进。

字典学习；稀疏表示；异常数据；鲁棒性

0 引 言

近年来，信号的稀疏表示模型已成为重要的科研议题并吸引着学者们的广泛关注[1]。传统的稀疏表示思路是基于固定正交基的变换，如傅里叶变换、离散余弦变换、小波变换、Curvele变换等。这些正交基虽然构造相对简单，计算复杂度低，但不能与图像本身的复杂结构最佳匹配，并不是最优的稀疏变换基。随着字典学习方法[2-4]的深入研究，人们开始根据信号本身来学习过完备字典，对稀疏编码研究的一个热点是信号在冗余字典下的稀疏分解。诸多研究成果表明，通过学习获得的字典原子数量更多,形态更丰富,具有更稀疏的表示，能更好地与信号或图像本身的结构匹配，为图像带来更大的压缩空间，在图像分类[5]、图像去噪[6]、图像修复[7]、图像超分辨率[8]等方面表现出了更优的性能。

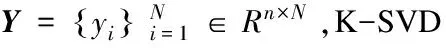
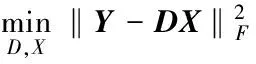
(1)

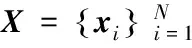
两种算法最主要的区别在于字典更新的方式不同。MOD算法在字典更新时，对整个字典一次更新，而K-SVD算法则是利用奇异值分解方式逐个更新字典原子，避免矩阵求逆计算的同时也提高了算法的收敛速度。

大多数的字典学习模型都是基于平稳的高斯白噪声假设而建立的，即每个训练信号可以表示为yi=Dxi+ni，其中ni为0均值的高斯向量。然而，在实际应用中，训练样本中除了含有轻微的高斯噪声外，还含有少量的异常值，这些异常值的存在将会影响字典学习方法的性能。为此，陈和吴[11]提出了一种鲁棒的字典学习方法，通过将重建误差分解为小而密的噪声和大而稀疏的异常值，同时考虑加性高斯噪声和稀疏损坏这两方面，以获得鲁棒字典；SajjadAmini等[12]则从另一个角度出发，研究了训练样本中含有异常值的情况，建立出鲁棒的字典学习模型，并利用优化算法学习鲁棒字典的同时，隔离了异常值。

文中基于文献[12]提出的鲁棒字典学习模型，采用交替近端线性化方法[13]求解非凸的最小l0范数，从含有异常值的训练样本中学习鲁棒的冗余字典。将所提算法用于视频帧图像去噪中，仿真对比实验结果表明，文中算法具有更好的去噪性能，且表现出了较好的鲁棒性。

1 鲁棒字典学习模型

考虑到训练样本中含有异常值的情况，将训练样本集中的每一个信号表示为如下的数学模型：

yi=Dxi+ni+oi

(2)

其中，ni为0均值的高斯向量；oi为异常值向量，当第i个训练信号为异常值时，oi≠0，否则oi=0。

为了获得鲁棒的字典学习模型，与文献[12]一样，假设异常值的数目远小于训练样本总数N，则考虑异常值情况下的鲁棒字典学习模型如式(3)所示：

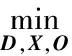
(3)

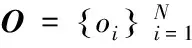
通过引入正则化参数λ2，式(3)可以转化为如下的无约束最优化问题。

(4)

式(4)中的模型扮演着双重角色：从训练样本集中学习字典D和隔离异常值。然而模型(4)是一个非凸优化模型，l0范数不可微且是NP难题，在多项式时间内只能求得次优解。一种最常用的做法是采用l1范数来最佳凸逼近l0范数[14]。文献[11]就是通过将l0范数模型转化为最小l1范数问题，并利用坐标下降法交替优化字典、稀疏表示系数和异常值，从而训练出鲁棒字典。

受文献[13]中所提交替近端线性化方法的启发，提出一种新的优化算法来求解式(4)的鲁棒字典学习模型。

2 算法设计与分析

文中所提算法是基于近端方法[15]而设计的，该算法求解的是式(5)所示的非凸问题：

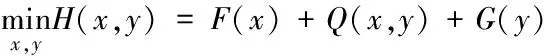
(5)

其中，F(x)，G(y)都是适当的下半连续函数；Q(x,y)是一个在任何有界集中都具有Lipschitz梯度的光滑函数。

文献[15]中所提出的近端方法是通过求解如下的邻近问题来更新(x,y)的估计：

(6)

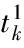
使用文献[16]中定义的邻近算子：

(7)

则对最小化问题(6)的求解等价于如下的近端问题[13]：

(8)

基于此，模型(4)可以表示为如下形式：

(9)

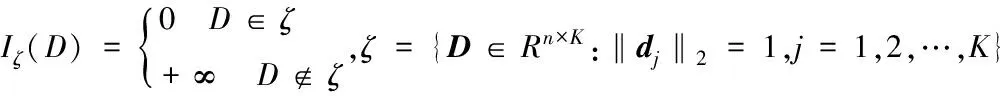
受交替近端线性化方法[13]的启发，采用交替迭代最小化的方式来更新D，X和O。

为了方便起见，使用上标(k)表示第k次迭代中的数值。

2.1 稀疏编码阶段

稀疏编码阶段，即为对X的求解。在第k+1次迭代时，给定D(k)，X(k)和O(k)，则有：

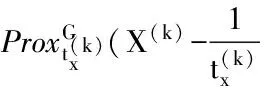
(10)

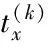
(11)

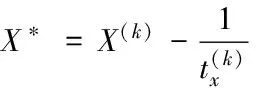
(12)

则X(k+1)的第(i,j)个元素可以很容易获得[13]：

(13)

2.2 字典更新阶段

这一阶段旨在更新字典D。由于D是列归一化的，因此可以逐列更新字典原子，即有：

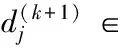
(14)

其中，

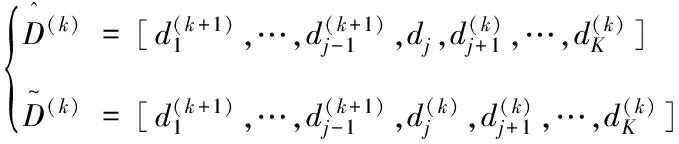
(15)

其中，qj是第j个元素为1、其余元素为0的K维向量。

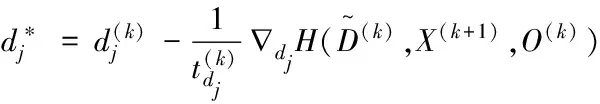
(16)

2.3 异常值更新阶段

给定D(k+1)，X(k+1)和O(k)，类似地，异常值的更新即为求解如下的优化问题：

(17)

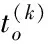
(18)

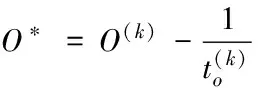
(19)

对式(19)进行求解，可得到O(k+1)的第(i,j)个元素为：

(20)

2.4 步长设置

(21)

3 仿真实验及结果分析

将所提新型鲁棒字典学习算法用于视频帧图像的去噪处理中，以验证其良好性能。采用格式为CIF的标准视频序列Foreman进行实验仿真，随机选取Foreman的第1、8、19、25、33、40帧作为测试样本集，如图1所示。实验中将大小为352×288的视频帧分成不重叠的8×8的图像块，并向每一块图像中加入均值为0、方差较低(σ2=102)的独立同分布的高斯白噪声，接着从中任选出r块(r=0,1,2,…且r≪1 584，表示异常值的块数)，再向这r块图像中加入均值为0、方差更高(σ2=302)的独立同分布的高斯白噪声，最后从含有异常值的图像块中训练冗余字典，以实现视频帧图像的去噪。设置所训练的字典原子数为256，ρ=1.1，μmin=0.1，最大迭代次数为30。实验平台为ThinkPadX1Carbon3rd,Windows7,Intel(R)Core(TM)i7-5600UCPU,2.6GHz,8GB，所有实验设计基于MatlabR2011a编程实现。

图1 测试图像集

分别采用DCT、K-SVD和所提算法对测试图像集中的每一视频帧进行去噪处理，图2给出了异常值块数为5时，三种算法从视频序列的第25帧中学习的冗余字典。

图2 三种算法训练出的冗余字典

从图2中可以看到，DCT训练出的字典原子形态最不丰富，采用K-SVD算法训练出的字典已能较好地与图像本身的结构相匹配，而文中算法所训练的字典原子形态最丰富，为图像带来了更大的压缩空间。

为了展示所提算法具有更好的去噪性能，图3给出了不同算法随异常值块数增加时去噪性能变化情况对比图。为了消除随机性，每一测试帧的PSNR取5次执行结果的平均值，且取6个测试帧的平均PSNR作为实验最终结果。

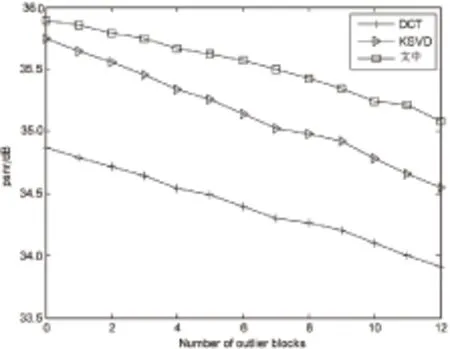
图3 6个测试帧的平均PSNR随异常值块数变化图

由图3可知，随着异常值块数的增加，三种算法的去噪性能都在降低，但所提算法表现出了更好的鲁棒性。其中，DCT的去噪性能最低，这是由于DCT采用的是正交变换，训练出的字典原子不丰富；虽然K-SVD算法训练出的字典已能较好地与图像本身的结构相匹配，但由于训练样本中含有异常值，而K-SVD算法无法隔离异常值，因此其去噪效果没有文中算法的效果好。

此外，图4中给出了异常值块数为8时，三种算法对Foreman第33帧去噪后的视觉效果图，进一步验证了文中算法具有更优的鲁棒性以及去噪性能。

图4 三种算法去噪后的视觉效果图

4 结束语

文中提出了一种新型的鲁棒字典学习优化模型，并采用交替近端线性化方法求解该模型，在学习冗余字典的同时也隔离了训练样本中的异常值。仿真对比实验表明，文中所提算法能提供很好的鲁棒性，并在图像去噪方面表现出了更优的性能。

[1]EladM.Sparseandredundantrepresentations:fromtheorytoapplicationsinsignalandimageprocessing[M].Berlin:Springer,2010.

[2] 练秋生,石保顺,陈书贞.字典学习模型、算法及其应用研究进展[J].自动化学报,2015,41(2):240-260.

[3]Kreutz-DelgadoK,MurrayJF,RaoBD,etal.Dictionarylearningalgorithmsforsparserepresentation[J].NeuralComputation,2003,15(2):349-396.

[4]RubinsteinR,BrucksteinAM,EladM.Dictionariesforsparserepresentationmodeling[J].ProceedingsoftheIEEE,2010,98(6):1045-1057.

[5]BahrampourS,NasrabadiNM,RayA,etal.Multimodaltask-drivendictionarylearningforimageclassification[J].IEEETransactionsonImageProcessing,2016,25(1):24-38.

[6]EladM,AharonM.Imagedenoisingviasparseandredundantrepresentationsoverlearneddictionaries[J].IEEETransactionsonSignalProcessing,2006,15(12):3736-3745.

[7]LiuJ,MaX.Animprovedimageinpaintingalgorithmbasedonmulti-scaledictionarylearninginwaveletdomain[C]//IEEEinternationalconferenceonsignalprocessing,communicationandcomputing.[s.l.]:IEEE,2013:1-5.

[8]LiuX,ZhaiD,ZhaoD,etal.Imagesuper-resolutionviahierarchicalandcollaborativesparserepresentation[C]//Datacompressionconference.[s.l.]:IEEE,2013:93-102.

[9]EnganK,AaseSO,HakonHJ.Methodofoptimaldirectionsforframedesign[C]//IEEEinternationalconferenceonacoustics,speech,andsignalprocessing.[s.l.]:IEEE,1999:2443-2446.

[10]AharonM,EladM,BrucksteinA.K-SVD:analgorithmfordesigningovercompletedictionariesforsparserepresentation[J].IEEETransactionsonSignalProcessing,2006,54(11):4311-4322.

[11]ChenZ,WuY.Robustdictionarylearningbyerrorsourcedecomposition[C]//ProceedingsoftheIEEEinternationalconferenceoncomputervision.[s.l.]:IEEE,2013:2216-2223.

[12]AminiS,SadeghiM,JoneidiM,etal.Outlier-awaredictionarylearningforsparserepresentation[C]//IEEEinternationalworkshoponmachinelearningforsignalprocessing.[s.l.]:IEEE,2014:1-6.

[13]BaoC,JiH,QuanY,etal.L0Normbaseddictionarylearningbyproximalmethodswithglobalconvergence[C]//ProceedingsoftheIEEEconferenceoncomputervisionandpatternrecognition.[s.l.]:IEEE,2014:3858-3865.

[14]ChenSS,DonohoDL,SaundersMA.Atomicdecompositionbybasispursuit[J].SIAMReview,2001,43(1):33-61.

[15]BolteJ,SabachS,TeboulleM.Proximalalternatinglinearizedminimizationfornonconvexandnonsmoothproblems[J].MathematicalProgramming,2014,146(1-2):459-494.

[16]RockafellarRT,WetsRJB.Variationalanalysis,volume317ofgrundlehrendermathematischenwissenschaften[M].Berlin:Springer,1998.

Sparse Representation of Video Frame Based on Novel Robust Dictionary Learning

QIAN Yang,LI Lei

(Center for Visual Cognitive Computation and Application,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

Dictionary learning is a very effective signal sparse representation method which has been widely used in the field of sparse signal processing.However,in practice,both training and testing samples may be corrupted and contain noises and a few outlier data,which may heavily affect the learning performance of it.Hence,in contrast to the conventional dictionary learning methods that learn the dictionary from clean data,a novel robust dictionary learning algorithm is proposed to handle the outliers in training data.In the proposed algorithm,the alternating proximal linearized method is used for solving the non-convexl0normbaseddictionarylearningproblem.Thus,therobustdictionarycanbelearnedandoutlierscanbeisolatedinthetrainingsamplessimultaneously.Thesimulationexperimentalresultsdemonstratethatthemethodhasthepromisingrobustnessandcanprovidesignificantperformanceimprovement.

dictionary learning;sparse representation;outlier data;robustness

2016-03-06

2016-06-23

时间：2017-01-04

国家自然科学基金资助项目(61070234，61071167，61373137，61501251)；江苏省2015年度普通高校研究生科研创新计划项目(KYZZ15_0235)；南京邮电大学引进人才科研启动基金资助项目(NY214191)

钱 阳(1991-)，女，硕士生，研究方向为非线性分析及应用；李 雷，博士，教授，研究方向为智能信号处理和非线性科学及其在通信中的应用。

http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1023.040.html

TP

A

1673-629X(2017)02-0037-05

10.3969/j.issn.1673-629X.2017.02.009