基于核密度估计的K-means聚类优化
熊开玲,彭俊杰,杨晓飞,黄 俊
(1.上海大学 计算机工程与科学学院,上海 200444;2.中国科学院 上海高等研究院 公共安全中心,上海 201210)
基于核密度估计的K-means聚类优化
熊开玲1,彭俊杰1,杨晓飞2,黄 俊2
(1.上海大学 计算机工程与科学学院,上海 200444;2.中国科学院 上海高等研究院 公共安全中心,上海 201210)
K-means聚类算法作为一种经典的聚类算法,应用领域十分广泛;但是K-means在处理高维及大数据集的情况下性能较差。核密度估计是一种用来估计未知分布密度函数的非参数估计方法,能够有效地获取数据集的分布情况。抽样是针对大数据集的数据挖掘的常用手段。密度偏差抽样是一种针对简单随机抽样在分布不均匀的数据集下容易丢失重要信息问题的改进方法。提出一种利用核密度估计结果的方法,选取数据集中密度分布函数极值点附近的样本点作为K-means初始中心参数,并使用核密度估计的分布结果,对数据集进行密度偏差抽样,然后对抽样的样本集进行K-means聚类。实验结果表明,使用核密度估计进行初始参数选择和密度偏差抽样能够有效加速K-means聚类过程。
K-means聚类;密度偏差抽样;核密度估计;数据挖掘
0 引 言
随着互联网、物联网等产业的发展,各种各样包含高维和海量的大规模数据集被生成。针对大规模数据的数据分析也变得越来越普遍[1]。K-means聚类算法作为一种应用广泛的经典聚类算法,在面对大规模结构复杂的数据时,与其他数据挖掘方法一样,表现得不太理想,主要集中在面对大数据时计算开销和时间开销成倍的增长和选择初始参数时变得极为困难两个问题上[2]。针对这样的情况,通常在应用特定的数据挖掘方法时(如聚类、关联规则等),往往引入抽样技术先从数据集抽取出一个样本,然后在这个样本数据集上进行处理,最后将处理结果推广到整个数据集[3]。简单随机抽样(SimpleRandomSampling,SRS)是一种简单高效的抽样方法。SRS应用广泛但在不均匀或者倾斜严重的数据集中效果得不到保证[4]。由于许多自然现象都遵循如Zipf定律、二八定律等不均匀分布,因此简单随机抽样在许多数据集中并不适用。为此Palmer等提出了密度偏差抽样方法(DensityBiasSampling,DBS)[5-6]。该方法被证明在分布不均匀的数据集中有较好的适应性,数据简约性能较好[7],但DBS需要预知数据集的分布。核密度估计(KernelDensityEstimation,KDE)是一种非参数估计方法,不需要有关数据分布的先验知识,是一种获取数据集未知分布的有效方法。因此可以使用核密度估计解决密度偏差抽样需要知道数据分布的问题。此外,针对数据集较稠密区域更容易成为类簇中心的特点[8],使用核密度估计的结果选择K-means的初始中心参数,并在大数据集时使用核密度估计的结果进行密度偏差抽样,然后使用抽样样本集进行聚类分析。实验结果表明,该方法可以在不影响聚类结果的情况下有效减少聚类过程的时间。
1 K-means聚类算法

K-means算法流程如下:
Step1:随机指定k个点作为初始化类中心点;
Step2:对每一个样本x,将其分配到离它最近的聚类中心;
Step3:重新计算各类中心;
Step4:使用新的类中心,进行Step2并计算偏差J;
Step5:如果J值收敛,则返回类中心C并终止算法,否则回到Step2。
作为一种基于划分的聚类算法,由于算法简单,容易理解,所以K-means算法应用广泛。但是,K-means聚类算法也有自身的局限性。主要缺陷表现如下[10]:
(1)K-means聚类算法需要预先给出簇的数目K。而在实际应用中,聚类数据集究竟需要分成多少类往往是未知的。
(2)K-means聚类算法的聚类结果受初始中心点选取的影响较大,初始中心点选取不当很容易造成聚类结果陷入局部最优解甚至导致错误的聚类结果。
(3)K-means聚类算法不适用于大数据集的聚类问题。K-means聚类算法迭代过程中每次都需对所有的数据点进行计算,因此面对大数据集时算法的计算开销巨大。
2 密度偏差抽样
随着互联网、物联网、大数据等领域的发展,大规模数据集越来越普遍,这些数据集的数据量对K-means算法所带来的计算复杂度可以说是灾难级的。由于K-means聚类算法在处理大数据集时的效果不能令人满意,并且该算法的计算开销较大。另一方面,由于大规模数据集本身的复杂度较高,因此对给定的大数据集进行数据挖掘时,通常都是先抽取一个样本数据集,然后在该样本数据集上进行处理,最后将样本集处理的结果推广到整个数据集。
简单随机抽样作为所有抽样方法的基础是目前应用最广泛的抽样方法,该方法虽然原理简单但效率较高。不过在不均匀或者倾斜严重的数据集中效果得不到保证。Palmer等提出的密度偏差抽样方法被证明在分布不均匀的数据集中有较好的适应性,数据简约性能较好。
密度偏差抽样是一种相对较新的抽样策略。其主要流程是,先将原始数据集分成不同的组,各组大小(所含数据点的数量)表示该组的密度,然后按以下原则进行抽样[11]:
(1)一个分组内各个数据点被抽到的概率相同;
(2)最终获取的数据样本集的分布特征与原始数据集的分布一致;
(3)各组抽样概率的偏差依据各组大小的偏差;
(4)期望的样本集的大小值已知。
综合上述原则,当数据集的分布为均匀分布时,各个分组的密度也应该是一致的,这时密度偏差抽样的结果与简单随机抽样的结果应该是一样的,因此,简单随机抽样可视为数据集在均匀分布密度偏差抽样的特例。相对于简单随机抽样,密度偏差抽样的优势主要是简约效果好、适应性强[12]。
图1中的原始数据是有20 000个数据点(x,y)的数据集,其中4个组都使用高斯分布生成。当对其进行2%的抽样时,发现进行DBS抽样两个较小的数据集能够保留在抽样结果中,但是使用SRS抽样时,较小的数据集完全消失了。通过结果对比可知,当数据集属于不均匀分布时,使用密度偏差抽样的结果较使用简单随机抽样时的结果更优。因此为了更好地保证抽样所得的样本集能够反映整个数据集的特征,需要知道数据集的密度分布。

图1 DBS与SRS的实验对比
3 核密度估计
核密度估计是求解给定的随机变量集合分布密度问题的非参数估计方法之一,用来解决与之相对的参数估计方法所获得结果性能较差的缺陷问题。在参数估计方法中需要先对数据集做相关假定数据集的分布,然后求解假定函数中的未知参数。但是通常假定的密度函数模型与实际密度函数之间相差较大。由于核密度估计不需要对数据集做相关假设,只是从数据集本身出发研究数据集的分布特征,所以KDE自提出以来就在各个领域广泛应用。
核密度估计定义如下:

(1)
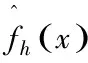

(2)

理论上,任何函数均可以做核函数,但是为了密度函数估计的方便性与合理性,通常要求核函数满足以下条件[14]:
(3)
常用的核函数有:
(1)高斯核函数(Gaussiankernel):
(2)矩形窗核函数(boxcar):

(3)Epanechnikov核函数:
(4)BiWeight核函数:
另外,窗宽参数h控制了在求点h处的近似密度时不同距离样本点对点密度的影响程度。当h选择过大时会出现过光滑情况(OverSmoothed),当h选择过小时会出现不够光滑(UnderSmoothed)的情况[15]。
如图2所示,使用正太分布随机产生100个随机数,虚线是其实际概率密度函数曲线,使用不同窗宽h进行核密度估计时,得出如图所示结果。当h=0.05时的KDE密度函数曲线波动频繁,当h=2时,曲线较为光滑但与实际相差甚远。在实际概率密度曲线与h=2之间的是h=0.337时的KDE密度函数曲线,该

图2 窗宽h值的选择对核密度估计的影响
曲线与实际曲线十分接近。


(4)
当对图1中的原始数据集进行高斯核估计时,可以得到如图3所示的密度分布。

图3 核密度估计
4 基于核密度估计的K-means聚类优化
由图3显示,原始数据集中数据点越稠密的地方密度函数值越大,而密度函数的极大值点也与原始数据集的稠密区域中心十分接近。因此为了减少K-means聚类的迭代次数,可以选择核密度函数的极大值点作为K-means初始迭代中心。另外,可以通过设置半径阈值,将距离小于半径阈值的极大值点归并到一个类;设置密度阈值,将密度小于密度阈值的极大值区域作为噪声去除,因为这些区域在整个数据集中所占的权重过低。通过半径阈值和密度阈值的过滤,就可以确定一个聚类数目K。当数据集较大时,可以使用核密度估计函数对数据集进行密度偏差抽样,以此来约简数据集。
步骤如下:
(1)对数据集进行高斯核密度估计获取数据集密度分布;
(2)根据密度分布设定半径阈值和密度阈值;
(3)根据半径阈值和密度阈值获取K-means算法的参数K和初始聚类中心;
(4)对数据集进行密度偏差抽样获取样本集;
(5)对样本集进行K-means聚类。
实验1使用来自UCIKDDArchive中的SyntheticControlChartTimeSeries的数据集(600条、维度为60维),数据样本较小,但维度较高。使用核密度估计选择的初始聚类中心和使用随机选择的初始聚类中心的K-means,在未使用密度偏差抽样的情况下进行多次实验。表1是两种情况下迭代次数对比以及样本点的类内总距离的对比,其结果表明,在聚类效果差不多的情况下,核密度估计初始参数选择的迭代次数较随机初始参数更少。

表1 利用核密度估计选择迭代初始参数与随机初始参数聚类对比
对图1所示的数据集,进行K-means和使用了核密度估计优化的K-means聚类分析。实验结果如表2所示。

表2 使用了核密度估计初始参数选择和密度偏差抽样的K-means结果对比
由于两次聚类结果一定会有差异,所以无法将两次结果中的类一一对应,因此为了方便对比实验结果,引入如下定义:

表2中的结果表明,使用核密度估计优化后的K-means迭代次数较少,结果与直接使用K-means的相差不大,并且迭代次数较为稳定,相比随机参数初始化的K-means受初始参数的影响较小。如第6组实验中,使用随机参数初始化的K-means就陷入了局部最优解,因此结果差距较大。
5 结束语
提出了一种利用核密度估计结果的方法。通过实验结果表明,使用核函数密度估计所选取的K-means初始参数,可以在尽量不影响聚类效果的基础上有效减少K-means的迭代次数,同时在数据集较大时,可以使用核密度估计的结果对数据集进行密度偏差抽样,有效地简约数据量,从而加速聚类过程。
[1] 程学旗,靳小龙,王元卓,等.大数据系统和分析技术综述[J].软件学报,2014,25(9):1889-1908.
[2] 孙吉贵,刘 杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.
[3] 张春阳,周继恩,钱 权,等.抽样在数据挖掘中的应用研究[J].计算机科学,2004,31(2):126-128.
[4] 盛开元,钱雪忠,吴 秦.基于可变网格划分的密度偏差抽样算法[J].计算机应用,2013,33(9):2419-2422.
[5]PalmerCR,FaloutsosC.Densitybiasedsampling:animprovedmethodfordataminingandclustering[J].ACMSIGMODRecord,2000,29(2):82-92.
[6]HotiF.Onestimationofaprobabilitydensityfunctionandthemode[J].AnnalsofMathematicalStatistics,2003,33(3):1065-1076.
[7] 李存华,孙志挥,陈 耿,等.核密度估计及其在聚类算法构造中的应用[J].计算机研究与发展,2004,41(10):1712-1719.
[8] 倪巍伟,陈 耿,吴英杰,等.一种基于局部密度的分布式聚类挖掘算法[J].软件学报,2008,19(9):2339-2348.
[9]MacQueenJB.Somemethodsforclassificationandanalysisofmultivariateobservations[C]//Proceedingsof5thBerkeleysymposiumonmathematicalstatisticsandprobability.California:UniversityofCaliforniaPress,1967:281-297.
[10]RosenblattM.Remarksonsomenonparametricestimatesofadensityfunction[J].TheAnnalsofMathematicalStatistics,1956,27:832-837.
[11] 余 波,朱东华,刘 嵩,等.密度偏差抽样技术在聚类算法中的应用研究[J].计算机科学,2009,36(2):207-209.
[12]DudoitS,FridlyandJ.Aprediction-basedresamplingmethodforestimatingthenumberofclustersinadataset[J].GenomeBiology,2002,3(7):1-21.
[13]JonesMC,MarronJS,SheatherSJ.Abriefsurveyofbandwidthselectionfordensityestimation[J].JournaloftheAmericanStatisticalAssociation,1996,91(433):401-407.
[14]Buch-LarsenT,NielsenJP,GuillénM.Kerneldensityestimationforheavy-taileddistributionsusingthechampernownetransformation[J].Statistics,2005,39(6):503-518.
[15]ParkBU,MarronJS.Comparisonofdata-drivenbandwidthselectors[J].JournaloftheAmericanStatisticalAssociation,1990,85(409):66-72.
K-means Clustering Optimization Based on Kernel Density Estimation
XIONG Kai-ling1,PENG Jun-jie1,YANG Xiao-fei2,HUANG Jun2
(1.School of Computer Engineering and Science,Shanghai University,Shanghai 200444,China; 2.Public Security Center,Shanghai Advanced Research Institute,Chinese Academy of Sciences, Shanghai 201210,China)
K-meansclusteringalgorithmisclassicalandwidelyusedinmanyfields,butithaspoorperformanceinthecaseofprocessinghighdimensionalandlargedatasets.Kerneldensityestimationisanonparametricestimationmethodtoestimatethedensityfunctionofunknowndistribution,whichcaneffectivelyobtainthedistributionofthedataset.Samplingisacommonmethodfordatamininginlargedatasets.Densitybiasedsamplingisanimprovedmethodfortheproblemofeasylossofimportantinformationwhenusingthesimplerandomsamplingintheinclineddataset.Amethodisproposedusingresultofkerneldensityestimation,whichchoosessamplepointsfromneighborhoodofpeakofdensityfunctionofdatasetastheinitialcenterparametersofK-meansandusesresultofkerneldensityestimationtoperformdensitybiasedsamplingonthedataset,thenrunsK-meansclusteringonthesampleset.TheexperimentalresultsshowthatusingthekerneldensityestimationforselectionofinitialparametersanddensitybiassamplecaneffectivelyacceleratetheK-meansclusteringprocess.
K-meansclustering;densitybiassampling;kerneldensityestimation;datamining
2016-03-28
2016-07-05
时间:2017-01-04
国家自然科学基金资助项目(61201446)
熊开玲(1992-),男,硕士研究生,研究方向为数据挖掘;彭俊杰,博士,副教授,硕士生导师,CCF高级会员,研究方向为云计算。
http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1039.074.html
TP
A
1673-629X(2017)02-0001-05
10.3969/j.issn.1673-629X.2017.02.001

