初中数学例题及习题教学设计研究

邱贞辉

摘 要：例题和习题的讲解是初中数学课堂教学的重要组成部分，也是初中生学习数学知识的主要途径，通过科学地设计例题和习题教学能够激发学习兴趣、培养良好品质，起到积极的反馈作用。教学中，教师可就数形结合思想、建模思想和变通思想等方面加以研究，通过对一元二次方程的教学设计，为数学例题及习题教学设计研究提供参考。

關键词：初中数学 例题及习题 设计 研究

课堂是学生学习知识的主要途径，因此教学质量的高低与课堂教学状况有着密切关系。在课堂教学中，例题及习题的教学与讲解会占用较多时间，因此要提高数学教学质量，必须加强对数学例题及习题的教学设计研究。

数学习题浩如烟海，在教学过程中不能面面俱到，但基本上可以分为代数题、平面几何题、立体几何题、解析几何题等。教师要充分利用各类例题和习题的功能来提高学生的学习效果。

一、例题及习题在教学中的作用

个体学习离不开对具体实例的认识，就像医生学习医术离不开对相关病例的研究。数学中的例题就是学生学习过程中的“病历”，学生通过对这些“病历”的研究，可学会更多的知识。数学例题具有基础性、启发性和创新性的特点，是各类数学知识的精华汇总，是连接课本知识与学生思维的纽带。

数学习题就像是医生的实习实验室，学生只有通过对数学习题的不断钻研与攻克，才能巩固所学知识，才能熟练地运用所学知识，进一步发展思维能力。数学习题能够给学生提供施展才能的平台，同时也是衡量学生学习状况的标准，通过对这些问题的解答，学生能够了解自己的学习状况，知道自己的弱点，从而调整自己的学习状态。

1.激发兴趣，培养良好品质

在数学教学实践中，我们可以通过对例题和习题的设计来激发学生的学习兴趣，从而促进学生获取新知识。例如，教师可以通过改编题干的方法，将学生喜闻乐见的事情转变为题干，调动学生的学习热情。另外，学生通过对例题和习题的练习，可以培养自己的逻辑推理能力和分析问题能力，还可以在潜移默化中改变性情，有助于形成追求真理的品质和实事求是的态度。通过对例题和习题解题思路的探求，能够培养学生独立思考和勇于探索的品质；通过对难题的钻研，能够培养学生锲而不舍和坚强的品质。

2.自我检测，获取信息反馈

学生的学习情况要通过对相应数学例题和习题的解答状况来体现。合理的问题设计可以了解近期的教学状况，反映学生学习中的不足以及对基本知识和技能的掌握情况。例如，每个知识点学完后，教师可以通过设计练习题的方式让学生把习题做到作业本上，使学生在做题的过程中进一步了解自己的学习状况，同时，也便于教师在批改作业的过程中掌握学生的学习状况。

二、例题及习题教学设计

1.突出例题及习题中的数学思想

数学思想是对数学本质的认识，是通过对数学问题的解答而总结出来的解题指导思想，是数学教学的灵魂。如果学生能够正确地掌握数学思想，就能使数学解题迎刃而解，便于数学知识的纵向迁移，使学生养成良好的数学能力，从而提高学生的数学成绩。

第一，数形结合思想的运用。我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休。”这句话强调了数形结合思想的重要性。例如，面积为1的矩形，它的周长的最小值是多少？周长为3的矩形，它的面积最大值是多少？对于这个问题，我们如果单纯地从代数角度来思考就会得出方程xy=1，x+y=3/2，这样一来，对于学生来说，运用所学知识解答问题就较为困难了。如果我们通过变形将方程xy=1，x+y=3/2，变换为y=1/x，y=-x+3/2，这样，就变成了学生所熟悉的反比例函数和一次函数了。这时再通过作图，在同一个直角坐标系中画出对应的图象，就能明显地得出结论了。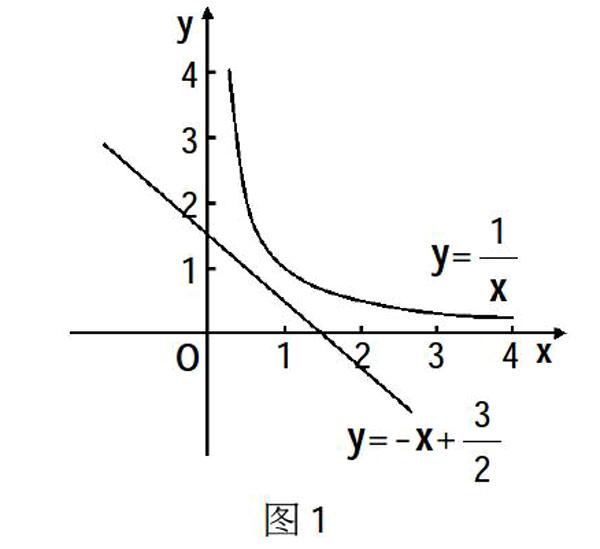

2.利用建模，培养学生的应用意识

新课标提倡教师在教学过程中应通过“创设情境—建立模型—解答应用”的模式进行教学，这就是数学教学中的建模意识，从本质上讲就是提出问题、分析问题、应用问题，是解决问题的一个过程。例如，一道与学生生活息息相关的题目：一家商店出售衣服，为了搞促销，先提高成本价的40%，然后又以8折出售，结果每件获得了15元的利润，问这件衣服的成本价是多少？这道题可以以一元一次方程为模型，设成本价为x元，那么每件衣服的标价就可以表示为（1+40%）x元，那么实际售价可以表示为（1+40%）×80%x元，利润可表示为[（1+40%）×80%x-x]元，列出方程（1+40%）×80%x-x=15。解题过程模型可以表示为图2，解答应用题就是创建这样一个模型的过程。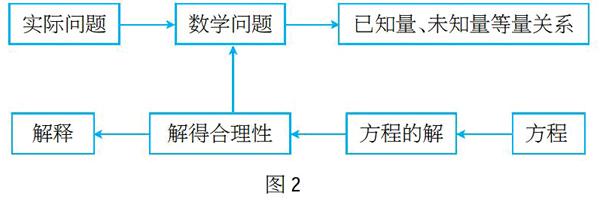

3.通过变通题目，促进学生的知识理解

数学题目浩如烟海，但万变不离其宗，都是通过几种数学知识演变而来的。在教学中，首先，教师应结合教材例题，通过改变命题方式和结构形式来帮助学生加深对某一知识点的理解。其次，通过对习题的不断变换，开拓学生视野，培养学生思维，提高解题能力。例如，在学习了“勾股定理”内容后，教师可提出以下问题，以帮助学生加深对知识的理解：（1）如果三角函数a2+b2=c2中a，b，c为锐角三角形的三条边，那么a2，b2，c2之间存在什么样的关系呢？（2）如果三角函数中a，b，c为钝角三角形的三条边，那么a2，b2，c2之间存在什么样的关系呢？（3）如果勾股数是满足方程a2+b2=c2的正整数解，那么方程an+bn=cn（n>2）有没有正整数解呢？通过对一系列问题的解答帮助学生加深对勾股定理的理解。

4.注重知识的整体性

数学知识不是孤立存在的，它是整体中的局部，只有对局部内容教学并与整体相联系后，才有利于学生对知识的理解、记忆、汇总与提取。例如，在学习“四边形”章节内容后，学生会对学到的平行四边形、菱形、正方形、矩形、等腰梯形等相關知识有所认识，这些知识都是零散的内容，如果不及时进行汇总与整理，就容易混淆。因此，教师可以通过引导学生绘制图表，对所学知识进行比较，使认知结构得到优化。例如，从四边形开始分支，什么样的四边形为平行四边形，什么样的图形为梯形；平行四边形可根据角的关系和临边关系分为矩形和菱形；根据它们的特殊性，总结出正方形的相关知识；梯形可根据腰和角的性质分为等腰梯形和直角梯形。

三、数学例题及习题教学设计案例

以初中数学一元二次方程教学设计为例，第一课时设计思路按照“设置情景—提出问题—建立模型分析问题—应用拓展”来设计。一元二次方程是中学数学的主要组成部分，首先根据教学点的需要引入了大量实例，教师应引导学生建立一元二次方程，通过对方程的化简变形来归纳出一元二次方程的概念。

1.创设问题情境，引入课程教学内容

（教师出示挂图，引导学生回答问题）

问题一：有一块长方形的地毯（见图3），四周镶有宽度相等的花边，地毯有8 m长，5 m宽，它中央长方形的图案有18平方米，问花边有多宽？

问题二：如图4所示，有一个长为10 m的梯子斜靠在墙上，梯子的最上端在距离地面8 m的地方，由于地滑，梯子的顶端下落了1 m，问梯子的底部到底滑了多远？

问题三：仔细观察等式102+112+122=132+142，是否还能找出另外一组五个相连的数字也符合这样的特点？

学生回答完问题后，教师继续引导学生思考：根据列出的方程，你发现与以前学过的方程有什么不同吗？相比以前学过的一元一次方程，你可以给现在的方程取一个名字吗？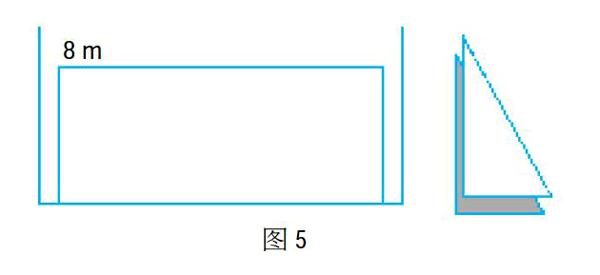

2.现实问题“数学化”，真正解决问题

教师可引导学生将一些实际问题转化为常见的数学问题后再解答，并画出数学简图（见图5）。

列出方程（8-2x）（5-2x）=18，（x+6）2+72=102，x2+（x+1）2+（x+2）2=（x+3）2+（x+4）2。深入剖析方程，将上述方程简化为2x2-13x+11=0，x2+12x-15=0，x2-8x-20=0。通过对方程ax2+bx+c=0中a，b，c三个数值的讨论，引出一元二次方程的条件。

3.巩固练习与反思

（1）把方程（2x+5）2=4（x-7）2转化为一元二次方程的一般形式，并找出它们的二次项系数、一次项系数和常数项。

（2）方程（a+3）x2-13x+11=0，当a满足什么条件时，该方程为一元二次方程？当a满足什么条件时，该方程为一元一次方程？

（3）方程（a+3）xb+1-13x+11=0，当b为多少时是一元二次方程？

通过对这些问题的练习，可以帮助学生充分认识一元二次方程，实现教学目标。

最后提出课后思考题：在一次同学聚会上，参加聚会的人两两握手，总共握了88次，问从握手的次数上能否判断出有多少人参加了聚会？

参考文献：

[1]龚新玲，当代中学生的心理特点及教育对策[J].兵团教育学院学报，2005（2）.

[2]蒋永鸿.关于新课程理念下的中学数学课堂教学设计问题的研究[D].兰州：西北师范大学，2004（55）.

[3]中华人民共和国教育部.全日制义务教育数学课程标准（实验稿）[S].北京：北京师范大学出版社，2005.