无鳍舵矢量推进水下机器人纵向稳定性研究

张荣敏, 陈原, 高军

(山东大学(威海) 机电与信息工程学院，山东 威海264209)

无鳍舵矢量推进水下机器人纵向稳定性研究

张荣敏, 陈原, 高军

(山东大学(威海) 机电与信息工程学院，山东 威海264209)

为了提高水下机器人低速航行时的机动性，提出了将一种基于球面并联机构的矢量推进螺旋桨应用于水下机器人，建立了旋量形式的六自由度运动学模型。针对矢量推进的二维转动角分解了矢量推力，得到了三维方向上的比例因子，基于牛顿-欧拉法建立了矢量推进水下机器人的动力学模型。同时提出了以矢量推进的比例因子作为输入量，利用拉普拉斯变换建立纵向运动的复数域扰动模型，基于扰动模型提出了无量纲化的矢量推进稳定裕度指标。数值算例验证了水下机器人无鳍舵矢量推进方式的有效性与稳定性。

水下机器人；矢量推进；并联机构；动力学；扰动模型；操纵稳定性

水下机器人在海洋资源勘测和开发中具有不可或缺的作用。矢量推进方式能够显著提高水下机器人低速航行时的定位能力，已经成为众多学者的研究热点[1-3]。作者设计了一个二自由度球面并联机构，并将其安装于水下机器人尾部，构成了一个螺旋桨矢量推进器[4]。该并联矢量推进器会随着偏摆角的变化产生多维方向推进力，从而能够实现单机构多姿态的矢量推进方式，但是同时会对水下机器人动力学模型及其操纵稳定性造成较大的影响。因而，对无鳍舵矢量推进水下机器人的操纵稳定性的研究具有重要意义。

现有的水下机器人动力学模型大多只针对螺旋桨推进器与鳍舵组合推进方式[5-12]。例如，黄海等[5]基于柱坐标系建立了欠驱动型水下机器人的动力学模型；Ba等[6]对一种喷水矢量推进水下机器人进行了矢量推进动力学建模；王树新[7]建立了混合驱动水下滑翔机的动力学微分几何模型。但是现有水下机器人的动力学模型大多针对鳍舵辅助导向方式而构建，本文以矢量推进偏摆角和螺旋桨转速为控制量，建立了矢量推进水下机器人的动力学模型。

另外，对水下机器人操纵稳定性的研究大多局限于鳍舵面水动力或内部质量分布等设计参数的时域稳定性分析。例如，魏延辉[13]研究了多翼自治水下机器人在外界干扰作用下的稳定性模型；赵宝强[14]分析了一种水下滑翔机器人的动态稳定性；Zhang[15]设计了一种不确定干扰模式下水下机器人的操纵稳定性分析方法。现有的时域操纵稳定性分析方法很难运用到无鳍舵矢量推进水下机器人中，本文提出以矢量推进的比例因子作为输入量，利用拉普拉斯变换方法建立纵向运动的复数域扰动模型，并且基于该扰动模型提出了无量纲化的矢量推进稳定裕度指标。

1 矢量推进水下机器人的运动学模型与坐标系

如图1所示为安装于水下机器人尾部的可控二自由度球面并联矢量推进器。水下机器人螺旋桨轴的姿态可通过二自由度球面并联机构进行控制。该球面并联机构为2-RPC& 2-RPCS型并联机构，其中R表示与静平台铰接的转动副，PC为弧形伸缩杆形式的移动副，其实质为变异转动副，S为球副。它由定平台、动平台以及连接它们的四条运动支链构成。其中RPC运动链和与之相邻的RPCS运动链为驱动支链，由伺服电机驱动并由锥齿轮传动，另外两条为对称的被动分支。螺旋桨主轴通过万向节联轴器传递主推电机的扭矩，进而实现水下机器人的俯仰和偏航运动。

图1 矢量推进器Fig.1 The vectored thruster

在水下机器人尾部安装图1所示的矢量推进器，就构成了如图2所示的矢量推进水下机器人。为描述水下机器人的运动，建立了如图2所示的固

定坐标系E-XYZ和船体坐标系B-xyz。固定坐标系的原点选在大地的某一点E处，EX轴在水平面内，以水下机器人初始航行方向为正，EY轴在垂直面内，垂直向上为正，EZ轴垂直于EXY平面，其正方向与EX、EY轴构成右手坐标系。在固定坐标系下，水下机器人的位置向量定义为R=(XYZ)T，姿态角向量设计为Λ=(φψθ)T，其中φ为横滚角，ψ为偏航角，θ为俯仰角，将其位姿向量写成如下旋量形式

(1)

船体坐标系的原点选在水下机器人的浮心B处，Bx轴沿机器人纵轴，指向前为正，By轴垂直于Bx轴，当机器人水平放置时指向上为正，Bz轴垂直于Bxy平面，其正向与Bx、By轴构成右手坐标系。在船体坐标系下，水下机器人的线速度向量设计为U=(uvw)T，角速度向量定义为Ω=(pqr)T，其中u、v、w和p、q、r分别为沿x、y、z轴的线速度和角速度，将其广义速度向量写成如下旋量形式

(2)

图2 矢量推进水下机器人的三维模型及其坐标系Fig.2 The 3D model and coordinate frame of vectored thrust underwater vehicle

船体坐标系下和固定坐标系下的线速度以及角速度间的关系表示为：

(3)

式中：S为船体坐标系到固定坐标系的旋转变换矩阵，C为姿态变换矩阵，分别如下

(4)

(5)

2 矢量推进水下机器人的动力学建模

2.1 矢量推进力分解计算

矢量推进器具有二维转动自由度，所以在船体坐标系中螺旋桨主轴可以实现水平方向和竖直方向的偏转。螺旋桨推力FT沿主轴方向，可以将推力按照推进器两个方向的偏转角度进行如图3所示的三维分解。其中A点为推力作用点；B点为水下机器人的浮心；δh为螺旋桨轴在水平方向的偏摆角，从机器人的尾部看去，以左偏为正；δv为竖直方向的偏摆角，从机器人的尾部看去，以下偏为正。两个角度正负的规定以确保推力正方向与船体坐标轴正方向一致。

利用空间几何学把矢量推力FT分解到船体坐标系B-xyz的三个坐标轴上，可以得到三个推力分量Fx，Fy，Fz。因此，可将FT写成如下的向量式

(6)

图3 矢量推进力的三维分解图Fig.3 The 3D decomposition of vectored thrust

(7)

(8)式中：MT为螺旋桨反作用转矩的大小，Kq为扭转力矩系数，ρ为水的密度，D为螺旋桨叶直径，n为螺旋桨转速。

另外，推力分量会使水下机器人产生绕y轴和z轴方向的转矩，设推力作用点A到浮心B点的距离为rAB，则两个转矩分别My=FzrAB和Mz=FyrAB。综上可以将矢量推进器产生的力和力矩表示为

(9)

2.2 流体力和回复力计算

水下机器人在运动过程中主要受到流体动力和其他外力的作用。流体动力包括惯性类流体动力fA和粘性类流体动力fV，惯性类流体动力与运动的加速度和角加速度有关，而粘性类流体动力与水下机器人的冲角、漂角、速度和角速度有关。惯性类和粘性类流体动力可分别由式(10)和(11)计算

(10)

式中：λij为附加质量系数，由于水下机器人关于坐标平面x-B-y和x-B-z对称，具有左右、上下对称的特点，因此附加质量系数可以简化，只取λ11、λ22、λ26、λ33、λ35、λ44、λ53、λ55、λ62、λ66这10项。

(11)

式中：CX(0)为零纵向力系数，即直航阻力系数；系数CYα表示垂向力CY对冲角α的线性导数；其他系数如CYr、CZβ、CMp含义同理，即CX、CY、CZ、CR、CM和CN分别表示横向力系数、垂向力系数、纵向力系数、横滚力矩系数、偏航力矩系数和俯仰力矩系数，上标α、β、p、q、r分别表示对冲角、漂角、横滚角速度、偏航角速度和俯仰角速度的线性导数。由于该水下机器人为单机构矢量推进方式，没有方向舵或尾翼等辅助导向装置，因此与舵角或者翼角相关的水动力系数均为零。

水下机器人的重力G沿固定坐标系中Y轴的负向，浮力B沿Y轴的正向，重力和浮力可以称为回复力FR。重力矩为重心的位置矢量RG与重力矢量的叉积，转换到固定坐标系中的回复力和力矩可通过式(12)计算

(12)

计算回复力和力矩得到其整体矢量式为

(13)

2.3 矢量推进动力学模型的构建

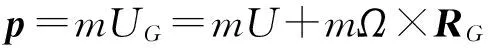
(14)

(15)

式中：m为水下机器人的质量，UG为水下机器人重心的速度，U为船体坐标系中原点的速度，Ω为水下机器人的角速度，RG为重心在船体坐标系的位置向量，J为水下机器人对原点的总惯量矩阵。

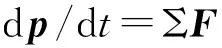
(16)

(17)

分别将式(14)和式(15)代入式(16)和式(17)，再结合前文对于矢量推进水下机器人的受力分析，可推出矢量推进水下机器人的空间平移运动方程和旋转运动方程为

(18)

(19)

式中：FA为惯性类流体动力，FV为粘性类流体动力，FR为回复力，FT为矢量推进器的推力，TA为惯性类流体动力矩，TV为粘性类流体动力矩，TR为回复力矩，MT为矢量推进器的推力矩。

将平移运动方程(18)和旋转运动方程(19)进行联立求解，并将前述各力和力矩的表达式代入可得动力学方程

(20)

式中：M为系数矩阵，f为水下机器人的广义外力(力和力矩)矩阵，它们分别表达为

(21)

(22)

由方程(20)可知，矢量推进水下机器人的动力学方程是以推进器的偏摆角和螺旋桨转速为控制量的。如果结合位姿运动学方程(3)，即可对该矢量推进水下机器人运动学及动力学进行求解。

3 纵向运动的操纵稳定性研究

3.1 操纵稳定性模型

纵向运动方向上的稳定性包括静稳定性和动稳定性，动稳定性是指水下机器人在运动过程中受到干扰后，能否恢复到原来运动状态的能力。其物理意义表达了水下机器人受到扰动后产生的倾覆力矩和阻尼力矩能否达到新的平衡状态[16]。

构建矢量推进水下机器人的纵向扰动方程是建立其操纵稳定性模型的基础。水下机器人在航行过程中，不可避免的会受到各种扰动。假设未扰动时的运动为定常直线运动，即浮心速度VT为常数，同时冲角近似为零。将上述条件代入动力学方程(20)，且略去二阶小量，可以得到时域内纵向扰动方程：

(23)

令a21=mxG+λ26，a22=0.5ρSLVT(μ->CYr)，a23=-> (m+λ22)，a24=->0.5ρVT2SCYα，a25=FT，a31=JZ+λ66，a32=0.5ρSL2VT(μxG/L->CNr)，a33=->(mxG+λ66)VT，a34=->0.5ρVT2SLCNα，a35=->rABFT，同时将纵向比例因子作为输入量，对方程(23)两边进行拉普拉斯变换，变换后得到如下矢量推进纵向扰动方程：

(24)

方程(24)是以比例因子Ky(s)为输入量，以r(s)，α(s)为输出量的二阶系统，它的齐次方程即为水下机器人的自由扰动方程。根据方程(24)可得俯仰角速度的复数域解为

(25)

利用输出的拉普拉斯变换与输入的拉普拉斯变换的比值得到俯仰角速度的传递函数Wr(s)为kr(s+s3)/(s+s1)(s+s2)，冲角的传递函数Wα(s)为kα(s+s4)/(s+s1)(s+s2)，当纵向比例因子为阶跃函数输入时，由拉普拉斯逆变换可分别得到俯仰角速度和冲角的过渡函数r(t)和α(t)：

(26)

式中：s1=[D1->(D12->4D0D2)0.5]/2D2，s2=[D1+(D12->4D0D2)0.5]/2D2，s3=r0/r1，s4=α0/α1，Kr=r0/D0，Kα=α0/D0，

其中，

D0=a22a34->a24a32，D1=a21a34+a22a33->a23a32->a24a31，D2=a21a33->a23a31，r0=a25a34->a35a24，r1=a25a33->a35a23，α0=a22a35->a25a32，α1=a21a35->a25a31，kr=r1/D2，kα=α1/D2。

由式(26)可以得到矢量推进水下机器人在受到扰动后，运动参数r(t)和α(t)的时间历程变化。如果各运动参数收敛，则说明水下机器人的运动状态是稳定的。

3.2 操纵稳定性指标

工程上常用纵向稳定裕度作为船舶等航行器的纵向稳定性指标。对于矢量推进水下机器人，其动力学模型与传统鳍舵式有所差别，无量纲旋转力臂不能只由传统水动力系数得到，还要包含矢量推进的比例因子项。因此提出了矢量推进的纵向稳定裕度来衡量其操纵稳定性。

由矢量推进的动力学方程(20)可以分别求得俯仰力矩N(r)和垂向力Y(r)。令d=rAB/L，将推力作用点与浮心之间的距离无量纲化，称其为无量纲推距。令FT′=2FT/ρVTSLr，称其为无量纲推力，同时无量纲质量为μ=2m/ρSL，将以上无量纲系数代入俯仰力矩N(r)和垂向力Y(r)中，可得到如下表达式：

(27)

纵向运动的旋转力臂是指俯仰力矩与垂向力的比值，由式(27)可求得矢量推进的旋转力臂Lr。按照式(28)将其无量纲化，然后按照稳定裕度的计算方法，可得到如式(29)所示矢量推进方式的纵向稳定裕度指标Gv。

(28)

(29)

由式(29)可知，与传统鳍舵式水下航行器相比，矢量推进的稳定裕度不仅与水动力系数有关，而且与无量纲推距和比例因子Ky有关。利用式(29)可以计算出矢量推进水下机器人的稳定裕度，然后采用以下准则进行稳定性判断，当Gv>1时，运动是静稳定的；当0≤Gv≤1时，运动是动稳定的；当Gv<0时，运动是动不稳定的[16]。

4 动力学行为及操纵性仿真算例

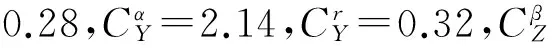
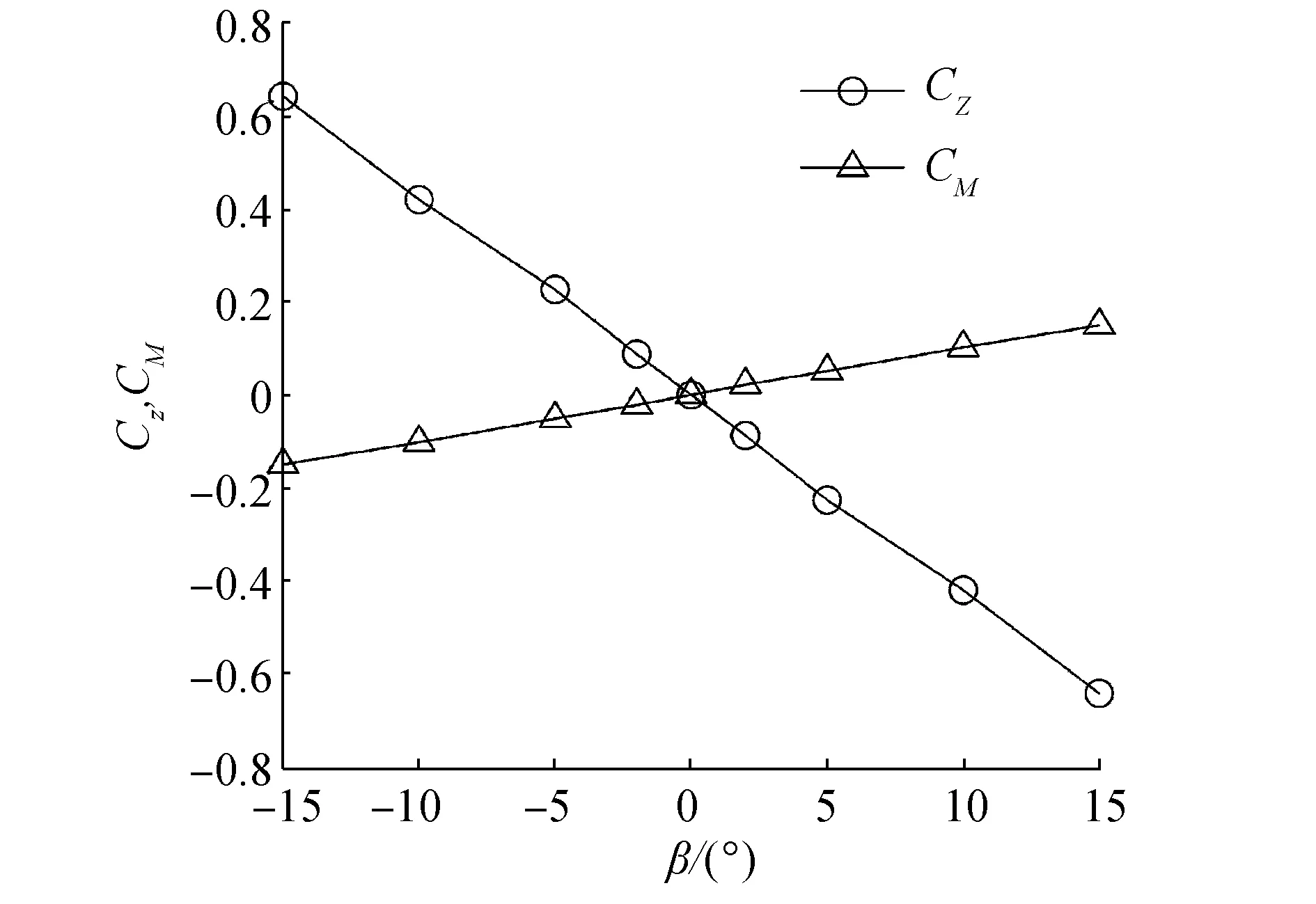
和

和

和

和图4 水动力特性仿真Fig.4 Hydrodynamics simulation

为验证该矢量推进方式的运动效果，采用四阶龙格-库塔方法对动力学方程组进行求解。水下机器人的质量m为53 kg，长度L为1.08 m，最大横截面面积S为0.05 m2，螺旋桨直径D为0.2 m，重心在船体坐标系中的坐标为(0 m,0.05 m, 0 m)。利用Matlab对其水平面回转、竖直面升潜和空间螺旋运动进行了运动仿真，仿真结果如图5～7所示。

图5 水平面回转运动Fig.5 Rotational motion in horizontal plane

图6 竖直面升潜运动Fig.6 Ascending and descending motion in vertical plane

如图5所示为水平面回转运动轨迹，控制量为螺旋桨转速n为600 r/min，推进器的水平偏摆角δh为15°，竖直偏摆角δv为0°，初始航行速度为0.01 m/s。由图可知，该矢量推进水下机器人从原点位置先做短暂的直线运动，然后很快的过渡到回转运动，回转半径约为25.5 m，其运动轨迹与传统鳍舵式相吻合。图6所示为水下机器人竖直面内的升潜运动仿真，其中控制量为螺旋桨转速600 r/min，水平偏摆角δh为0°，竖直偏摆角先为-10°，再为10°。图7所示为水下机器人空间螺旋运动的仿真，其中控制量为螺旋桨转速600 r/min，竖直偏摆角δv为15°，水平偏摆角δh为10°，其螺旋运动的升距约为4 m。对水下机器人空间运动轨迹的仿真结果与理论相吻合，表明了水下机器人动力学模型的正确性。

图7 空间螺旋运动Fig.7 Spiral motion

图8 比例因子Fig.8 The scaling factor

图8为比例因子的三维图，从图中能够看到随着矢量推进器水平偏摆角δh和竖直偏摆角δv的变化(->0.52≤δh≤0.52，->0.52≤δv≤0.52)，三个方向推力分量的变化趋势。在整个工作空间内，Fx能够达到不低于75%的推力，当δh=0、δv=±0.52时，和δv=0、δh=±0.52时，Fy和Fz能够达到最高50%的推力。

当水下机器人的矢量推进器在纵平面内受到单位阶跃偏摆的扰动时，俯仰角速度和冲角的过渡曲线如图9所示。从图中可以直观的看到过渡时间和稳态值。当t趋向于无穷大时，r(t)和α(t)是收敛的，这表明了当矢量推进水下机器人受到单位阶跃扰动时，它具有动稳定性。同时利用式(29)计算得到纵向稳定裕度Gv的值为0.703 6，这进一步证明了其运动是动稳定的。如图10所示为在单位阶跃扰动下矢量推进水下机器人纵向运动俯仰角和深度的过渡曲线，由图可看出，当t趋向于无穷大时，θ(t)趋向于一条直线，Y(t)趋向于二次曲线。图11所示为矢量推进水下机器人的纵向偏摆角为正弦输入时，俯仰角速度r的频率特性曲线，从图中可以看到幅频值Lr和相位差φr随偏摆角频率ω的变化趋势。当角频率ω趋向于0时，幅频值约为2.04 dB，相位差约为-1.03°，该频率特性表现出矢量推进水下机器人系统的稳定性。

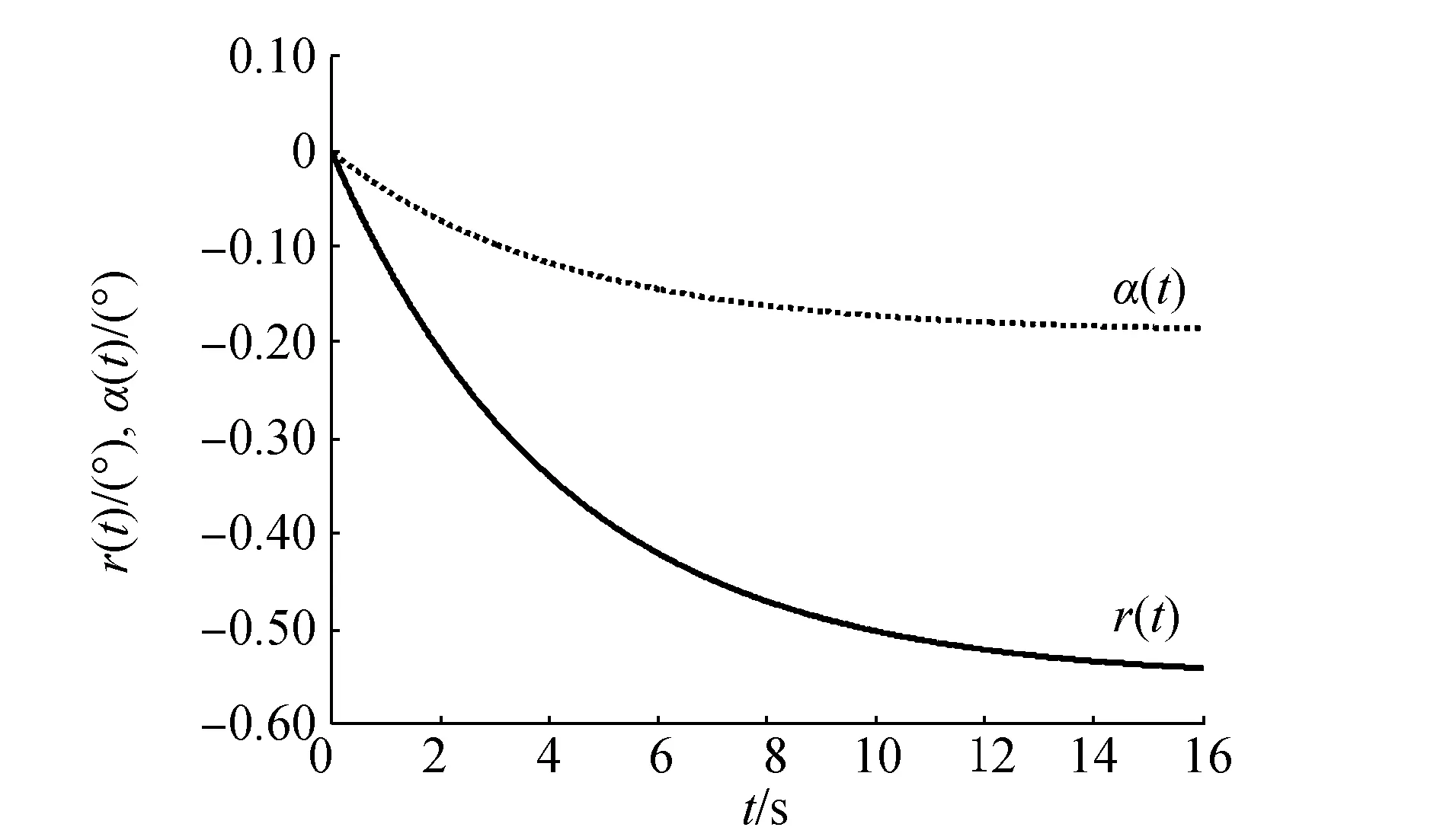
图9 r(t)和α(t)过渡曲线Fig.9 Transition curve of r(t) and α(t)

图10 θ(t)和Y(t)过渡曲线Fig.10 Transition curve of θ(t) and Y(t)

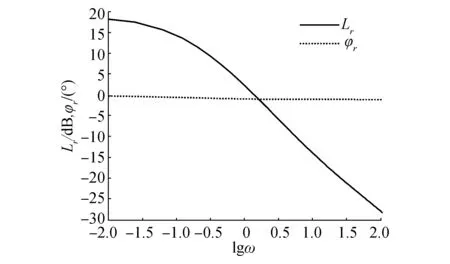
图11 俯仰角速度r的频率特性Fig.11 frequency characteristic of r

5 结论

1)安装有二自由度螺旋桨矢量推进器的水下机器人能够完成俯仰和偏航及其组合运动，实现了单机构多姿态的矢量推进方式。

2)对矢量推进水下机器人动力学方程的求解及其仿真分析实现了空间运动轨迹的可视化。其回转运动和螺旋运动表现出矢量推进方式的可行性和灵活性。

3)对水下机器人的纵向扰动模型仿真计算，得到了各运动参数的响应曲线，结果证明了各运动参数的收敛性，同时计算了矢量推进纵向稳定裕度的值为0.703 6，这些表明了矢量推进水下机器人的动态稳定性。

[1]陈世利, 卫民, 李一博, 等. 基于双闭环的矢量推进器的AUV转向控制方法[J]. 天津大学学报: 自然科学与工程技术版, 2014, 47(6): 530-534. CHEN Shili, WEI Min, LI Yibo, et al. Steering control strategy of AUV with vectored thruster based on double-loop mode[J]. Journal of Tianjin university: science and technology, 2014, 47(6): 530-534.

[2]BUGROVA A I, BUGROV G E, BISHAEV A M, et al. Experimental investigation of thrust-vector deviation in a plasma thruster[J]. Technical physics letters, 2014, 40(2): 161-163.

[3]袁伟, 俞孟蕻, 朱艳. 动力定位系统舵桨组合推力分配研究[J]. 船舶力学, 2015, 19(4): 397-404. YUAN Wei, YU Menghong, ZHU Yan. Research on thrust allocation of dynamic positioning vessels with propeller-rudder pairs[J]. Journal of ship mechanics, 2015, 19(4): 397-404.

[4]张荣敏, 陈原, 高军. 矢量推进解耦球面并联机构动力学研究[J]. 农业机械学报, 2015, 46(6): 319-326. ZHANG Rongmin, CHEN Yuan, GAO Jun. Dynamic analysis of decoupled spherical parallel mechanism for vectored thruster[J]. Transactions of the Chinese society for agricultural machinery, 2015, 46(6): 319-326.

[5]黄海, 张强, 张树迪, 等. 欠驱动AUV自适应编队控制策略[J]. 哈尔滨工程大学学报, 2015, 36(5): 633-637, 643. HUANG Hai, ZHANG Qiang, ZHANG Shudi, et al. Adaptive formation control strategy for under-actuated AUVs[J]. Journal of Harbin engineering university, 2015, 36(5): 633-637, 643.

[6]BA Xin, LUO Xiaohui, SHI Zhaocun, et al. A vectored water jet propulsion method for autonomous underwater vehicles[J]. Ocean engineering, 2013, 74: 133-140.

[7]王树新, 刘方, 邵帅, 等. 混合驱动水下滑翔机动力学建模与海试研究[J]. 机械工程学报, 2014, 50(2): 19-27. WANG Shuxin, LIU Fang, SHAO Shuai, et al. Dynamic modeling of hybrid underwater glider based on the theory of differential geometry and sea trails[J]. Journal of mechanical engineering, 2014, 50(2): 19-27.

[8]张铭钧, 刘维新, 殷宝吉, 等. 自主式水下机器人故障特征增强方法[J]. 哈尔滨工程大学学报, 2014, 35(9): 1099-1105. ZHANG Mingjun, LIU Weixin, YIN Baoji, et al. Fault feature enhancement for autonomous underwater vehicles[J]. Journal of Harbin engineering university, 2014, 35(9): 1099-1105.

[9]PARK J, KIM N. Dynamics modeling of a semi-submersible autonomous underwater vehicle with a towfish towed by a cable[J]. International journal of naval architecture and ocean engineering, 2015, 7(2): 409-425.

[10]刘鹏, 苏玉民, 李宁宇. 波翼相位差对柔性翼水动力性能的影响[J]. 哈尔滨工程大学学报, 2016, 37(3): 313-319.

LIU Peng, SU Yumin, LI Ningyu. Effects of wave phase difference on the hydrodynamic performance of a flexible flapping foil[J]. Journal of Harbin engineering university, 2016, 37(3): 313-319.

[11]CHEN Yuan, ZHANG Rongmin, ZHAO Xingyu, et al. Adaptive fuzzy inverse trajectory tracking control of underactuated underwater vehicle with uncertainties[J]. Ocean engineering, 2016, 121: 123-133.

[12]ELNASHAR G A. Dynamics modelling, performance evaluation and stability analysis of an autonomous underwater vehicle[J]. International journal of modelling identification and control, 2014, 21(3): 306-320.

[13]魏延辉, 杜振振, 陈巍, 等. 多翼自治水下机器人动力学建模与姿态控制[J]. 华中科技大学学报: 自然科学版, 2015, 43(6): 106-111. WEI Yanhui, DU Zhenzhen, CHEN Wei, et al. Dynamic modeling for multi-wing autonomous underwater vehicle motion control system[J]. Journal of Huazhong university of science and technology: natural science edition, 2015, 43(6): 106-111.

[14]赵宝强, 王晓浩, 姚宝恒, 等. 水下滑翔机李雅普诺夫稳定性分析[J]. 哈尔滨工程大学学报, 2015, 36(1): 83-87. ZHAO Baoqiang, WANG Xiaohao, YAO Baoheng, et al. Lyapunov stability analysis of the underwater glider[J]. Journal of Harbin engineering university, 2015, 36(1): 83-87.

[15]ZHANG Xiaoyu, HAN Yuntao, BAI Tao, et al. H∞ controller design using LMIs for high-speed underwater vehicles in presence of uncertainties and disturbances[J]. Ocean engineering, 2015, 104: 359-369.

[16]李天森. 鱼雷操纵性[M]. 2版. 北京: 国防工业出版社, 2007. LI Tiansen. Torpedo manoeuvreability[M]. 2nd ed. Beijing: National Defense Industry Press, 2007.

[17]张宏伟. 可着陆水下自航行器系统设计与动力学行为研究[D]. 天津: 天津大学, 2007. ZHANG Hongwei. System design and dynamical behavior of autonomous underwater vehicle with the capability of landing on the seafloor[D]. Tianjin: Tianjin University, 2007.

Longitudinal handling stability of vectored thrust underwater vehicle without fin and rudder

ZHANG Rongmin，CHEN Yuan，GAO Jun

(School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai 264209, China)

A single-mechanism vectored thrust approach without fin and rudder was proposed to improve the maneuverability of an underwater vehicle running at low speed. A new vectored thruster based on spherical parallel mechanism was applied to an underwater vehicle, and a six degrees-of-freedom kinematic model in the form of spinor was established. With the two-dimensional rotation angle of the thrust vectoring as the target, the vector thrust was decomposed, and the three-dimensional scaling factor was derived. A dynamic model of the vectored thruster was established on the basis of Newton-Euler method. In addition, with the scaling factor of thrust vectoring as an input, Laplace transformation was employed to establish the disturbance model along the vertical direction in a complex domain, and the dimensionless stability margin of vectored thrust based on the disturbance model was proposed. Numerical simulations were performed to verify the effectiveness and stability of the vectored thrust mode without fin and rudder.Keywords：underwater vehicle; vectored thrust; parallel mechanism; dynamics; disturbance model; handling stability

2015-09-30.

时间：2016-12-12.

国家自然科学基金项目(51375264)；山东省科技重大专项(2015JMRH0218)；山东省优秀中青年奖励基金项目(BS2013ZZ008)；中国博士后特别资助项目(2014T70632).

张荣敏(1986-)，男，博士； 高军(1968-), 男, 教授, 博士生导师; 陈原(1976-), 男, 副教授,博士.

陈原, E-mail:cyzghysy@sdu.edu.cn.

10.11990/jheu.201509089

U664.8

A

1006-7043(2017)01-0133-08

张荣敏, 陈原, 高军. 无鳍舵矢量推进水下机器人纵向稳定性研究[J]. 哈尔滨工程大学学报， 2017, 38(1): 133-139，152. ZHANG Rongmin，CHEN Yuan，GAO Jun. Longitudinal handling stability of vectored thrust underwater vehicle without fin and rudder[J]. Journal of Harbin Engineering University,2017, 38(1): 133-139,152.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161212.0920.002.html