浅谈中学生数学思维品质的培养

李园园�お�

[摘要]所谓思维品质是指学生在思维过程中个性的表现，是学生健全发展不可缺少的一部分内容.

在素质教育思想的影响下，

为了培养学生的数学思维品质，提升学生的数学素养，教师要认真贯彻落实“以生为本”的教学理念，组织多种活动，构建高效课堂.

[关键词]初中数学思维品质深刻性发散性

[中图分类号]G633.6[文献标识码]A[文章编号]16746058（2016）290028

众所周知，初中数学是九年义务教育阶段的必修课，初中是学生打好数学基础的重要阶段.但是，在以往的教学中，我们关注的仅仅是学生对基础知识的掌握和应试能力的提高，再加上大量的练习导致数学给学生留下的印象仅是抽象、枯燥的，嚴重不利于数学课堂价值的实现，也不利于学生综合能力的提高.所以，在素质教育思想的影响下，教师要更新教育教学理念，组织有效的数学教学活动，培养学生的思维品质.下面，本文就对如何在初中数学教学中培养学生的思维品质进行论述.

一、动手证明，培养学生数学思维的深刻性

所谓数学思维的深刻性是指思维活动的抽象程度和逻辑水平.动手操作可提高学生的知识应用能力，锻炼学生的操作能力，培养学生思维的深刻性.所以，在新课程改革下，教师要相信学生，鼓励学生

大胆地运用所学知识

对相关的概念、命题或综合性的练习题进行自主分析和证明.这样不仅能培养学生数学思维的深刻性，而且能使学生养成良好的自主学习的习惯.

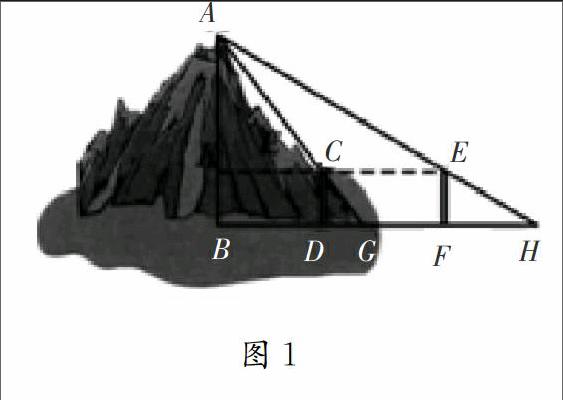
【例1】如图1，为了求出海岛上的山峰AB的高度，在D处和F处树立标杆CD和EF，标杆的高都是3丈，D、F两处相隔1000步，（1丈=10尺，1步=6尺），并且AB，CD和EF在同一平面内，从标杆CD后退123步的G处，可以看到顶峰A和标杆顶端C在一条直线上；从标杆EF后退127步的H处，可以看到顶峰A和标杆顶端E在一条直线上.求山峰的高度AB及它和标杆CD的水平距离BD各是多少步.（提示：连接EC并延长，交AB于点K，用含AK的式子表示KC和KE）

该题是九年级下册P93中的第12题，是拓展探索中的一道题.对很多学生来说，这道题是难题，因为该题出现在最后一题，再加上题目出现了一些学生不常见到的“丈”“步”等距离单位，学生一下子就没有了解题思路，原本并不太难的题目就因为心理作用变成了难题.而这种现状严重不利于高效课堂的构建，也不利于学生数学思维品质的培养.所以，在教学时，我鼓励学生大胆地对该题进行分析和思考，引导他们理解题意，找到与该题类似的原型，即分析该题的本质.这样，问题就转化为在Rt△ABH中，D、G、F均在BH上，EF⊥BH，EF交AH于点E，且CD⊥BH，CD交AG于C.其中，CD=EF=3丈，DF=1000步，DG=123步，FH=127步，求AB的高度和BD的长度.

这样剖析题目，既减少了学生的恐惧感，提高了学生的解题效率，而且有利于培养学生数学思维的深刻性.所以，在综合习题的解答中，教师一方面要鼓励学生大胆地解答，另一方面要引导学生学会拆分题目、分析题目.这样才能有效提高学生灵活应用知识的能力，提高学生的思维品质.

二、一题多解，培养学生数学思维的发散性

顾名思义，一题多解就是针对同一问题找到多种解题思路的一种方式，是发散学生思维，培养学生创新精神的有效方法之一.在新课程改革下，教师要鼓励学生多思考、多探究，有效培养学生数学思维的发散性，使学生获得良好的发展.

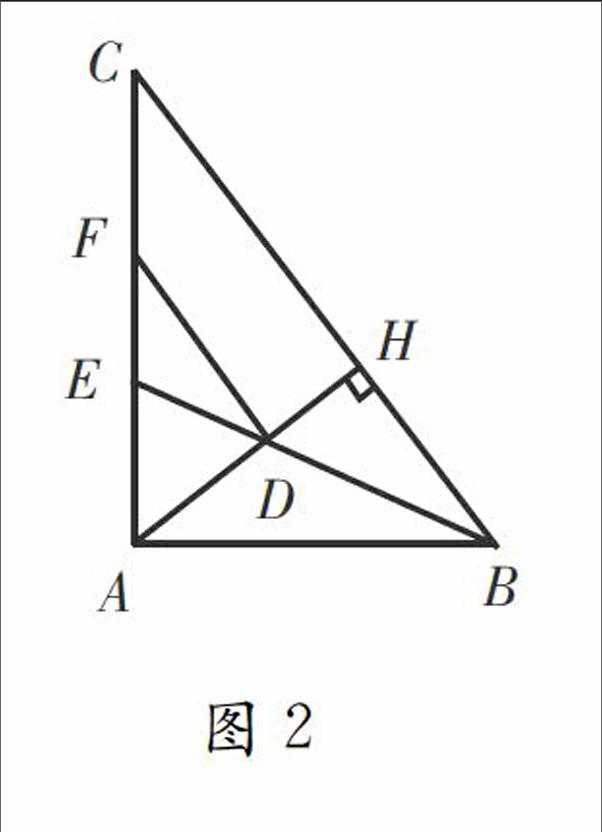
【例2】如图2，在△ABC中，∠A=90°，∠B的平分线交AC于点E，交BC边上的高AH于点D，过D作DF∥BC交AC于点F，求证：AE=CF.

虽然这只是一道基础性题目，但是，我还是要求学生进行一题多解，目的是培养学生从多角度思考问题的意识和思维品质，提高学生灵活运用知识的能力和解题能力.所以，在本题的解答中，我组织学生对该题进行了“多解”活动.比如，有学生提出：过E点作EK⊥BC于点K，通过证明Rt△ADF≌Rt△EKC，即可证明结论正确.还有学生提出：可以借助三角形的内角平分线定理证明△ABD∽△CBE……

组织学生大胆地进行思考，对题干进行分析和研究，引导学生在独立思考和合作交流中找到更多的解题思路，能有效培养学生思维的发散性，提高学生的数学学习能力.

总之，在新课程改革下，教师要充分发挥学生的主体性，要通过组织多种活动来培养学生的数学思维品质，为学生的全面发展奠定基础.

[参考文献]

霍海鹰.初中数学教学中如何培养学生的思维品质[J].学周刊，2014（16）.

（特约编辑嘉卉）