一种改进的支持向量机参数优化方法

赵朝贺

（1.安徽省电力设计院有限公司，安徽 合肥 230601）

一种改进的支持向量机参数优化方法

赵朝贺1

（1.安徽省电力设计院有限公司，安徽 合肥 230601）

为了保证支持向量机在提高核参数寻优效率的同时，拥有较高的学习精度，深入研究了核参数对支持向量机分类的影响，分析了网格搜索法和双线性搜索法的优缺点，并以此为基础提出了一种改进的参数优化方法。实验结果表明，该算法在保证支持向量机获得较高学习精度的同时能大大缩短参数寻优的时间，证明了该算法的优越性。

支持向量机；RBF核函数；参数优化；网格搜索；双线性搜索

支持向量机（SVM）是基于小样本统计理论提出的一种新的机器学习方法，在处理小样本、非线性及高维向量上展现出其独特的优势，已成为机器学习、模式识别、信息提取等领域的研究热点，受到众多研究者的广泛关注。实践证明，核参数和惩罚系数对SVM性能有着很大的影响，只有选择合适的核函数及其参数才能得到具有良好推广能力的SVM分类器[1]。

当前国际上对核参数的选择还未形成统一模式，主要靠经验和试算来解决，包括实验法、网格搜索法、双线性搜索法、遗传算法和粒子群算法等。其中，实验法耗时且难以获得最优参数，网格搜索法精度高但非常耗时，双线性搜索法效率高但精度一般，遗传算法和粒子群算法较为复杂且容易陷入局部最优。综合考虑以上常用参数寻优算法的优缺点，提出了一种改进的参数寻优方法。它能在大幅度减少参数寻优时间的同时，使SVM获取较高的学习精度。

1 SVM理论基础

SVM的原理是用分离超平面作为分离数据的线性函数，解决非线性分类问题，即升维与线性化[2]。其最优分类形式为：搜索一个分类超平面，能让两类无错误地分开，且样本的分类间隔最大。其基本的数学公式为：在条件的约束下，求函数的极小值。其中，w为超平面的法向量；b为超平面的平移量；C为惩罚系数，目的是控制误差ξ边界的平衡。

引入拉格朗日乘子αi，解算上述优化问题得到分类函数为：

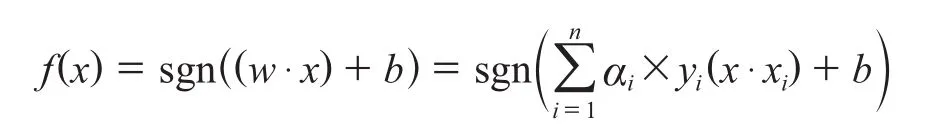
根据泛函数理论，在满足K(x·xi)=φ(x)·φ(xi)条件下，解算上述问题获得最终分类函数为：

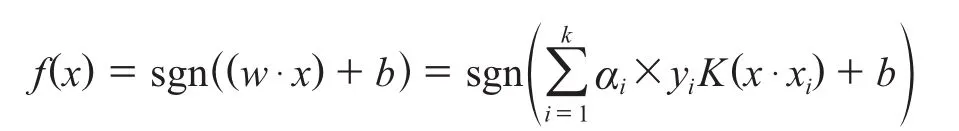
其中，核函数K(x·xi)有多种形式：线性核K(x·y)=x·y；多项式核K(x·xi)=(x·xi+1)d，d是自然数；RBF核（Gaussian径向基核）γ＞0； Sigmoid核K(x·xi)=tanh(v(x·xi)+c)。

2 核参数对SVM的影响

2.1 核参数对SVM推广能力的影响

核函数形式的不同决定了SVM模型的差异，用户总是想使用推广能力最好的分类模型，但推广能力却无法通过确切的值来表示。文献[3]总结的常用评估泛化误差方法中，最为经典是交叉验证法（CV），其基本思想是将训练样本均匀分为K组，对每个子集作学习分类测试，其余K−1个子集作为负样本，测试完成后将获得K个训练模型，K-CV的正确率由这K个模型最终测试集正确率的平均值来表示。通常情况下，K值会大于2，而实际操作中K值一般最小取3，只有当样本数据量很小是，K值才可能取2。K−CV能有效避免应用中产生过学习及欠学习的现象，且最终得到的验证结果说服力较强。

2.2 核参数对SVM分类性能的影响

评价SVM分类器的好坏，主要从它的推广能力和准确度来考虑。较多相关文献证明，选取何种核函数对SVM分类性能影响不大，主要影响因子是核函数的参数及误差惩罚因子C[4]。核函数中应用表现能力最好的是学习能力较强的RBF核函数，无论维数高低，样本数据量大小，适用性都表现较好，收敛范围较宽，是常用核函数中较为推崇的分类核[5]。因此RBF的核参数γ以及C便是影响SVM分类性能的主要因素，它们不仅影响SVM分类器的复杂性还影响着SVM的推广能力。本文将通过实验分析参数(C,γ)对SVM分类性能的影响。

2.2.1 误差惩罚参数C的影响

C的作用是在给定的特征子空间中，通过变化SVM分类器的置信域与经验风险的比值来推动SVM的推广能力，直至达到最好。若C越小，则表明对此模型经验误差惩罚较轻，SVM分类器的复杂性降低而经验风险增大；若C→∞，则必须要满足所有约束条件，即表明训练样本要保证全部无错误地被分开。所以一定至少存在一个误差惩罚参数C使得SVM的推广能力达到最佳。

由图1可知，当C取值较小时分类正确率较低，随C的增加分类正确率也急剧升高，即SVM的分类能力得到快速提升；当C大于某个阈值时，分类正确率变化不大，趋于稳定，表明此时SVM的分类性能对C的变换不再敏感。图1中在logC＞1.0时，SVM分类准确率已达到一个较高水平，随C增加分类正确率只是在某一值附近波动。利用这一现象和推论，可加快C的计算速度，完成C的初始搜索：首先从较小的C开始搜索，逐步增大C的取值，当SVM分类正确率不再增加时，认为C已处于“好区”，把该值作为SVM最优惩罚参数的初值。

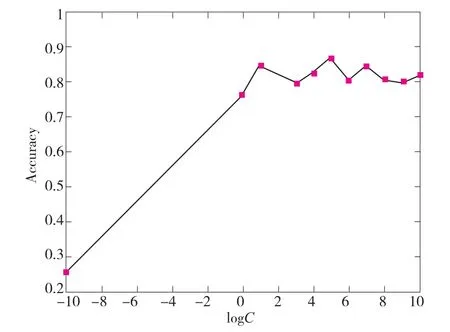
图1 分类正确率随C的变化趋势

2.2.2 核参数γ的影响

由于数据特征空间、核函数以及映射函数三者之间存在一一对应的关系，一旦核函数被确立，则映射函数和数据特征空间的关系也就被唯一确定。线性分类超平面的VC维数以及分离最优超平面的最小经验误差值的大小都由特征子空间的维数决定。若维数过高，则导致SVM的最优分类超平面变得较复杂，置信区间过大而经验风险过小；反之亦然。当γ取值在两端时，SVM分类器的推广能力都不会很好，因此只有合适的核参数才能将原始样本空间映射到最佳的特征子空间中，得到合适的、推广能力最佳的SVM[6]。

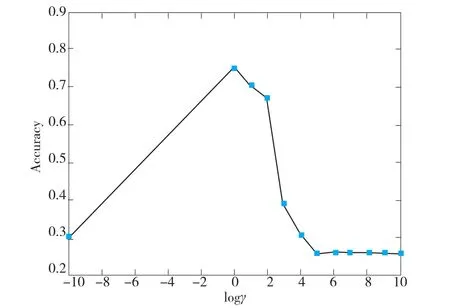
图2 分类正确率随γ值的变化趋势

由图2可知，SVM分类器的分类质量直接受核参数的影响。随着γ值的增加，SVM分类正确率先由低到高；达到峰值后便由高到低逐渐下降到趋于稳定，此时SVM分类准确率较低。SVM分类准确率随γ值大幅度变化表明核参数γ可以控制其灵活性，当γ值较大时，核函数则变为一个常函数。从分类正确率随γ的变化趋势，可明显看出存在一个峰值，对应的γ值此时最佳，说明“好区”是存在的，关键是选择最优的γ值。

通过实验分析分类正确率与参数(C,γ)的关系，可估计C的最优近似值，缩小参数空间的搜索范围；再搜索“好区”的核参数γ，进一步提高搜索参数(C,γ)的效率和准确度，从而提高SVM的分类精度。

3 SVM核参数寻优算法

对于RBF核参数(C,γ)的优化选择有多种，参数(C,γ)的差异决定了SVM的不同，常见的核参数寻优算法主要有双线性搜索法[7]和网格搜索法两种。

3.1 双线性搜索法

双线性搜索法计算(C,γ)最优组合的原理主要是利用参数(C,γ)的差异决定SVM的不同这一思想。文献[7]指出，参数空间大致可划分为3种：欠学习区、过学习区和好区（见图3）。

大量实验证明：在以(logC,logγ)为坐标的参数空间中，最优的参数组合(C,γ)会集中在“好区”直线logγ=logC−log附近，可使SVM分类精度的达到最高，即图中“好区”的虚线附近。因此，双线性搜索算法实现参数优化的步骤为：

1）利用线性核SVM解算最优C，使得此时线性核的SVM学习精度最高，把此时解算的C记为

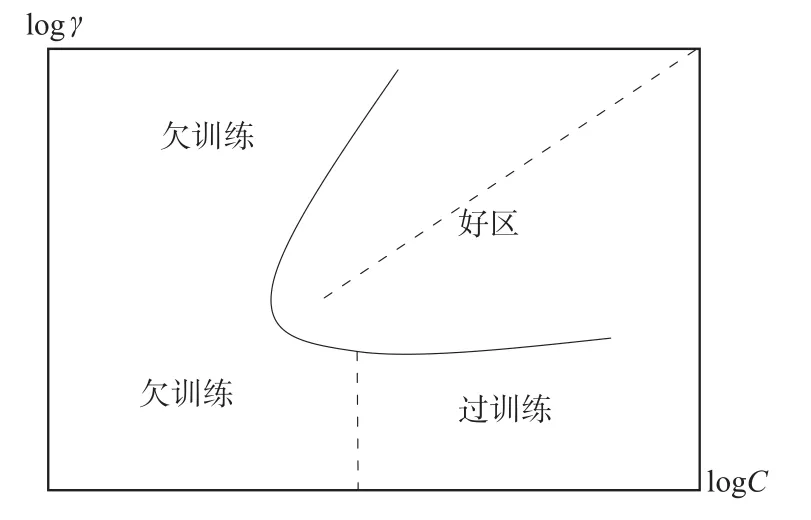
图3 不同参数空间的SVM性质

3.2 网格搜索法

网格搜索法[8]的原理是将C和γ分别取i和j个值，得到i×j个(C,γ)组合，分别训练各组合参数，将学习精度最高的那对参数作为搜索的最佳参数组合，为了得到较高的分类精度，参数C和γ的步长通常为0．1。

分析上述两种搜索策略可以看出：以网格搜索算法获得的参数组合(C,γ)求解的SVM学习精度较高，数据计算量大，时间代价昂贵；双线性搜索算法运算速度较快。在以RBF核为基础的SVM参数搜索阶段，网格搜索算法代价为O(N2)，双线性搜索算法代价为O(N)。此外双线性搜索算法最优参数组合获取的精度较大程度地依赖于线性核SVM中的准确度。

3.3 改进的参数搜索法

在分析两种搜索算法主要影响因素的基础上，为了较少计算量和运行时间，提高SVM的分类精度，本文对参数寻优算法进行了改进，主要步骤为：

4 实验验证

为了验证本文改进的参数搜索算法的效率、有效性以及学习精度，分别将网格搜索法、双线性搜索法和本文参数搜索算法进行比较分析。在Microsoft Windows 7操作系统下，基于VS2008和LibSVM 3．1．7集成开发环境编写了算法实验程序。实验数据采用基于均值漂移的图像分割算法[9]获得的资源三号测绘卫星影像分割对象单元，从中选择330个训练样本，并将其分成4种类别，选用颜色矩特征作为特征向量进行测试。实验中C值范围为[2-10,210]、γ值范围为[210,2-10]，由于传统方法中步长一般为0．1，而起初SVM的正确率随C值增加显著，因此本文算法将C值初始步长设为1，γ值初始步长扩大100倍，设定为10，测试中逐次减小参数(C,γ)的步长。采用K-CV方法对正确率进行测试，K值为5，则3种参数寻优算法测试结果如表1所示。

从表1不难看出，网格搜索法耗时最长，本文算法在保证SVM分类精度的同时，大大缩短了参数寻优的时间。实验结果表明，对于庞大训练数据集，本文算法在相对较少的时间内，能够使SVM分类器获得较高的学习精度。

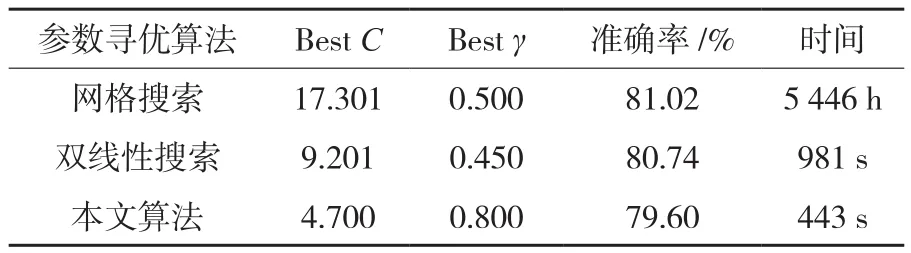
表1 3种参数寻优方法比较

[1] Chapelle O, Vapnik V, Bousquet O． Choosing Multiple Parameters for Support Vector Machines[J]．Machine Learning, 2002,46(1/3):131-159

[2] SU C T, YANG C H． Feature Selection for the SVM: an Application to Hypertension Diagnosis[J]．Expert Systems with Applications,2008,34(1):754-763

[3] 宋晓峰,陈德钊,胡上序．支持向量机泛化能力估计若干方法[J]．计算机科学,2004,31(8):125-126

[4] 刘大宁, 杨永乐, 白林． SVM核函数对分类精度影响的研究[J]．佳木斯大学学报(自然科学版),2012(4):627-630

[5] 宋晖,薛云,张良均．基于SVM分类问题的核函数选择仿真研究[J]．计算机与现代化,2011,30(8):133-136

[6] Keerthi S S, LIN C J． Asymptotic Behaviors of Support Vector Machines with Gaussian Kernel[J]．Neural Computation, 2003,15(7):1 667-1 689

[7] 李琳,张晓龙．基于RBF核的SVM学习算法的优化计算[J]．计算机工程与应用,2006,42(29):190-192,204

[8] 王兴玲,李占斌．基于网格搜索的支持向量机核函数参数的确定[J]．中国海洋大学学报(自然科学版),2005,35(5):859-862 [9] 余国斌,陈爱斌,孙华,等．基于Mean Shift的高分辨率遥感影像分割方法[J]．中南林业科技大学学报,2012,32(10):168-172

P237

B

1672-4623（2017）01-0053-03

10.3969/j.issn.1672-4623.2017.01.016

赵朝贺，硕士，主要从事工程测量及模式识别等方面的研究。

2015-10-26。

项目来源：国家自然科学基金资助项目（41371438）。