重视解决问题过程中的策略研究
倪红飞
(太仓市教师发展中心 江苏 苏州 215400 )
重视解决问题过程中的策略研究
倪红飞
(太仓市教师发展中心 江苏 苏州 215400 )
高考物理中的能量问题,每年都有一些颇有新意的试题,从不同的思维层面考查了学生创造性解决问题的能力.有些试题表面上看似乎平淡无奇,其实暗藏玄机,触到了考生的软肋.究其原因,在平时的习题教学中忽视了解决问题过程中的策略研究,导致学生学习过程中对解决问题方法的应用不能做到举一反三、触类旁通,更不能从策略研究高度认清解决问题中的思想方法的核心.所以,只有真正重视解决问题过程中的策略研究,才能从根本上提高学生分析问题和解决问题的能力.
平时教学中,要注意解决问题中的策略研究,让学生体验解决问题策略的多样性,真正发展学生解决问题过程中的实践能力和创新精神,这远比解决问题本身更为重要.
下面结合案例的分析,说明策略研究在解决问题过程中的重要性以及“解决问题的策略研究”的过程中,应该注意以下一些问题.
1 变换思维角度突出转化思想
案例一:瞬时功率问题
下面是关于功率问题设计的高考题.
【例1】如图1所示,细线的一端固定于O点,另一端系一小球.在水平拉力作用下,小球以恒定速率在竖直平面内由A点运动到B点.在此过程中拉力的瞬时功率变化情况是( )
A.逐渐增大
B.逐渐减小
C.先增大,后减小
D.先减小,后增大
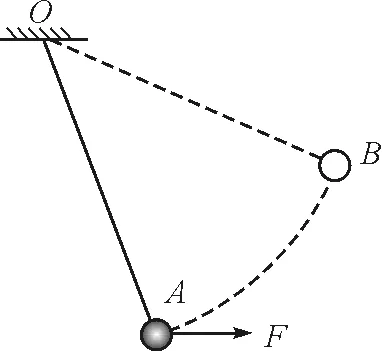
图1 例1附图
由于小球以恒定速率由A点运动到B点过程中.拉力在不断增大,而同时,小球水平方向的分速度在不断减小,所以,拉力的瞬时功率的变化一下子无法确定.
产生问题后,如何找到解决问题的途径,这是需要学生亲自经历探索的过程.
学生思考后,给出了2种典型的方法(体现了解决问题过程中两种不同的的策略).
方法一:计算法.
设F与速度v的夹角为θ,根据力的分解,在切线上(速度方向上)合力为零,即
mgsinθ=Fcosθ
又因为拉力的瞬时功率
P=Fvcosθ
所以
P=Fvcosθ=mgvsinθ
随θ增大,P增大,答案为A.
方法二:转化法.
小球以恒定速率在竖直平面内由A点运动到B点过程中,水平拉力F做的功与克服重力做的功相等,所以它们的功率大小也相等.小球由A点运动到B点过程中,由于小球沿竖直方向的分速度逐渐增大,因此克服重力做功的功率逐渐增大,即在此过程中拉力的瞬时功率也逐渐增大,选项A正确.
得到结论后,对2种方案进行了比较.
初看两种方法好象差别不大,进一步比较发现,方法一更多地体现了知识应用的技巧;方法二由于对原问题先进行了转化,把研究拉力的瞬时功率问题转化为研究重力做功的功率的问题,问题一下子变得豁然开朗,从中更能感受到解题者智慧的力量.这才是物理研究中应该突出的思想.
如果我们一厢情愿地告诉学生解决问题的策略,学生容易产生厌烦的情绪.所以首先要创设合适的情境,让学生在在解决问题过程中体会到策略的好处,使“解决问题的策略研究”变成了学生自身的需要.
2 巧妙组合过程凸显问题本质
策略形成的过程是学生不断探索的过程,绝对不能把策略研究变成的简单模仿训练,探索策略形成的过程比形成的策略更重要.
案例二:“环、杆”问题中的研究
2015年高考江苏卷第9小题是一个关于能量的试题,原题如下.
【例2】如图2所示,轻质弹簧一端固定,另一端与质量为m,套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v,恰好能回到A;弹簧始终在弹性限度之内,重力加速度为g,则圆环( )
A.下滑过程中,加速度一直减小

D.上滑经过B的速度大于下滑经过B的速度
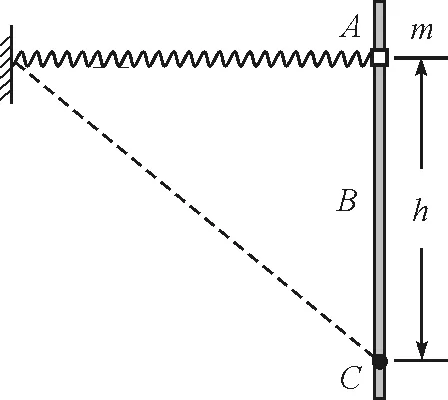
图2 例2附图
试题中叙述了2个过程:
(1)圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零;
(2)圆环在C处获得一竖直向上的速度v,恰好能回到A.
选项A,从动力学的角度讨论了加速度与受力的关系,考生大多能顺利作出判断:从A处由静止开始下滑到达C过程,圆环先做加速度不断减小的加速运动,再做加速度不断增大的减速运动.
选项B,C,D的判断是整个题目的核心.
开始时,大多数学生采用的方法是,分过程应用动能定理方程,联立解方程求解的思路.
圆环从A处由静止开始下滑到C过程,运用动能定理
mgh-Wf-Ep=0
圆环在C处获得一竖直向上的速度,恰好能回到A过程,运用动能定理
联立解方程得
对圆环从A处下滑到B过程运用动能定理
再对圆环从B处上滑到A的过程运用动能定理
联立解方程得
所以
vB>vB′
答案为B,D.
虽然,经过艰难的运算得到答案.但一个选择题,其解题过程如此繁杂,这种解题方案显然不是命题者的原意.
那么,该题的解决难道还有更好的策略?
由于分过程应用动能定理的方法,让大家吃尽了苦头,激发大家寻求更好的解题策略的需要.
其实,这个问题解决的核心,是如何把表面上互相独立的两个过程,通过问题转化的策略组合起来.如果,将原题的过程进行有机的组合,可以把两个过程设计成如下的过程:圆环先从C处获得一竖直向上的速度v,恰好能到达A,再从A处由静止下滑,经过B处的速度最大,回到C处的速度为零.
这样,由于全过程重力与弹力均不做功,全过程应用动能定理
很容易得到
选项B正确.
在下滑过程应用动能定理
mgh=Wf+Ep
得到
选项C错误.
同样的,对上滑过程经过B的速度与下滑过程经过B的速度的比较,也可以重新设计物理过程.从B点上滑,到下滑过程经过B全过程,应用动能定理
即上滑经过B的速度大于下滑经过B的速度.
将表面上互相独立的两个过程,通过问题转化的策略,组合成一个有机的整体是这个问题解决的关键.
由于在解决问题过程中,融入了更多学生探索的过程,使策略形成的过程真正成为学生思维完善的过程.
3 发现思维盲区培养反思精神
平时教学中要重视反思意识的培养,因为反思的过程可以使解决问题的思想得到了升华,对发展学生创新精神更具意义.
案例三:测定木块与桌面之间的动摩擦因数
下面是笔者根据高考试题的改编题.
【例3】为测定木块与桌面之间的动摩擦因数,小亮设计了如图3所示的装置进行实验.实验中,当木块A位于水平桌面上的O点时,重物B刚好接触地面.将A拉到P点,待B稳定后静止释放,A最终滑到Q点.分别测量OP和OQ的长度h和s.改变h,重复上述实验,分别记录和几组实验数据.

图3 例3附图
(1)请根据表1的实验数据作出s-h关系的图像.

表1 实验数据
(2)实验测得A,B的质量分别为m=0.40 kg,M=0. 50 kg.根据s-h图像可计算出A木块与桌面间的动摩擦因数μ=______.(结果保留一位有效数字)
以下是正确的解答.
(1)s-h图像如图4所示.
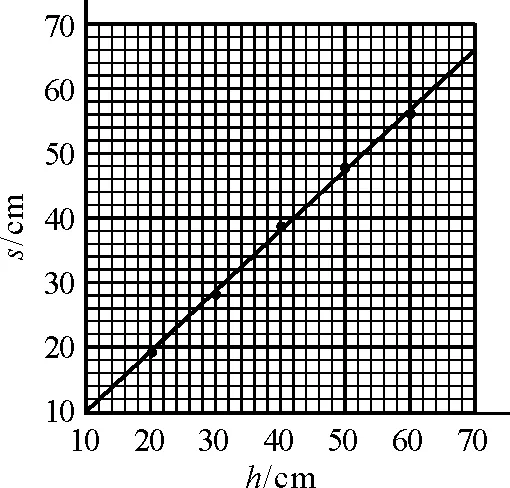
图4 s-h图像
(2)本实验测动摩擦因数的原理是动能定理.
B拉着A向下加速过程,对AB组成的系统应用动能定理
B接触地面后木块A继续滑行过程,对A应用动能定理
求得
图像的斜率
即
解得
μ=0.4
本题学生学生争论的焦点是,本题在应用动能定理列方程时,为什么不能把B拉着A向下加速过程和B接触地面后木块A继续滑行过程视为一个整体,对AB组成的系统应用动能定理,根据
Mgh-μmg(h+s)=0
解得
μ=0.6
这样研究问题的策略行不行?这个方法的错误关键在哪里?
这样类似问题的教学中,很多教师都遇到过相同的困惑,尽管课上对问题产生的根源分析得头头是道,但碰到同样类型的问题,学生照旧犯同样的错误.这个问题值得反思:在策略形成的过程中,是不是我们的教学过于粗暴了,把策略研究也变成的简单灌输,忽视了策略形成的过程中学生的反思过程.策略研究只有在反思中才能得到升华,学生的反思需要教师足够的耐心,再加上一点智慧.
所以,把解决问题的过程,更多植入了学生自我反思的种子.
(1)容易产生的盲区
全过程对系统应用动能定理是一个不错的思想,但是,列方程时容易产生一个盲点,B接触地面时,B与地面发生了碰撞,碰撞过程也产生的内能,如果把这部分能量损失考虑在内,原方程应为
Mgh-μmg(h+s)=Q
公式中的Q就是B与地面发生了碰撞产生的内能
由于
求得
解得
μ=0.4
结论相同.又由于B与地面发生碰撞时速度的计算,仍然要对加速过程分析,两种方案在处理问题差别不大.
(2)另一种纠错的思路
能不能既全过程应用动能定理,又避开B与地面发碰撞产生的内能问题?
这个崭新的方案引起了学生的思考.
有学生发现了解决问题的方案.可以全过程对木块A应用动能定理
Fh-μmg(h+s)=0
公式中的F是B拉着A向下加速过程中细线对A的拉力.
因此,先应用牛顿运动定律
Mg-F=Ma
F-μmg=ma
算出细线拉力
求得
解得
μ=0.4
结论也相同.
由于问题的探究过程,充分融入了学生的自我反思过程中的探索和思考,使策略形成的过程真正成为学生思维完善的过程,形成策略的过程,使学生收获了比策略更重要的东西.
2016-06-29)

