地震激励下储罐内液体的减晃试验研究及有限元分析

祁永成， 邱洪兴， 马涌泉

(东南大学 土木工程学院，南京 210096)

地震激励下储罐内液体的减晃试验研究及有限元分析

祁永成， 邱洪兴， 马涌泉

(东南大学 土木工程学院，南京 210096)

为了避免因液体晃动过大而引起的储罐“象足”型失稳破坏，采用减晃板作为抑晃装置并对其进行了减晃优化设计。分别采用缩尺模型试验(缩尺比1∶30)和有限元分析等手段对有、无安装减晃板的储罐内的液体晃动波高、罐底剪力及罐壁压应力等关键指标进行了实测和仿真模拟。研究结果表明：关键指标的模拟值与实测值较为接近，进而验证了储罐减晃有限元分析的可靠性；当减晃板在距液面0.125倍～0.225倍的储罐高度且其宽度在0.15倍的储罐半径附近时，减晃板对储液晃动波高、罐底剪力及罐壁压应力都具有较好的抑制效果；减晃优化设计后，“象足”失稳区(接近罐底处)的罐壁压应力峰值得到了较为显著的抑制。

立式储罐；地震激励；减晃板；模型试验；有限元

储液晃动问题是引起储罐破坏的主要原因之一，由于其多存储易燃易爆、有毒介质，一旦在地震中发生破坏，易导致火灾、泄露等次生灾害，对人类的生存和生态环境造成严重的影响。因而《立式圆筒形钢制焊接油罐设计规范》(GB 50341—2014)[1]要求：固定顶油罐和浮顶油罐的设计最高液位到罐壁上沿的距离应大于液面晃动波高。可见晃动波高是储罐罐高设计的一个重要参数，若能有效减小储液的晃动问题，将对储罐的优化设计带来良好效果。

为了抑制储液在地震作用下的剧烈晃动，学者们开展了相关的减晃研究工作。HASHEMINEJAD等[2]提出了一套简化公式用于计算带有竖向减晃板的椭圆形储罐的自振特性；ESWARAN等[3]使用VOF 技术研究了带隔板立方储液罐的减晃特性；王佳栋等[4]采用分离变量法研究了水平简谐激励作用下带环形隔板圆柱形储液罐中液体晃动响应；BISWAL等[5]提出了一种用于求解带刚性减晃板的矩形储罐非线性晃动响应的数值方法；柳伟等[6]基于概率密度演化理论分析了带有环形隔板罐体中流体的晃动响应。虽然这些研究都取得了一定成果，但是研究手段仍以理论仿真分析为主，尚缺乏相应的试验验证。

本文以1 000 m3立式石油储罐为工程背景，利用相似比理论设计多组储罐模型，并用有限元软件ADINA建立储罐的相应数值分析模型，探讨在地震激励下，有、无减晃板，减晃板的相对宽度及相对位置等因素对储罐液体晃动波高、基底剪力以及罐壁应力的影响，并将它们的结果进行对比分析，为数值分析提供试验验证，得出的结论可为相应储罐的减震设计提供参考。

1 模型试验

以1 000 m3的常用储罐原型背景,其基本参数见表1。试验采用有机玻璃(PMMA)代替钢材，AKYILDIZ等[7-9]已证明了其可行性；同时为了试验安全，采用以水代油，孙建刚[10]已证明影响很小。

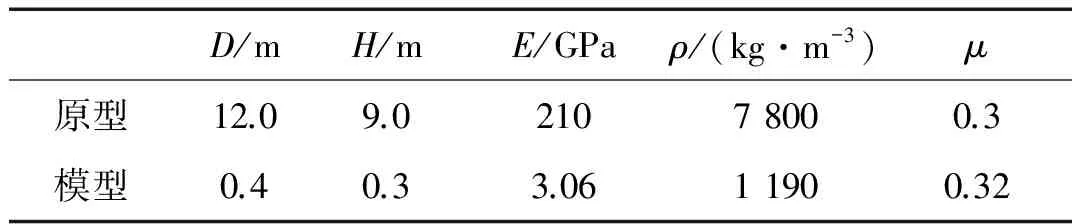
表1试件参数

注：D为储罐直径；H为储罐高度；E为弹性模量；ρ为储罐密度；μ为储罐泊松比模型比例为1∶30，根据动力试验相似比原则设计相同尺寸的立式储罐构件21个，其中1个无减晃板储罐，编号Y0，20个有减晃板储罐，编号Y1-Y20，四种尺寸的减晃板20片，编号F1-F20。构件模型如图1所示，参数如表2所示。

表2 减晃板参数

注：r代表减晃板宽度；h代表减晃板距液面的高度；R代表储罐半径；H代表储罐高度；定义r/R为相对宽度，h/H为相对位置，如图1所示

试验在东南大学结构试验中心进行。WS-Z30小型精密振动台系统为单水平向，电磁式激振，铝合金台面，台面尺寸506 mm×380 mm×22 mm，最大承载模型重35 kg，最大加速度10 g，最大行程±8 mm，频率范围0.5～3 500 Hz。试验加载装置如图2所示。

图1 试验模型(mm)Fig.1 Test specimen (mm)

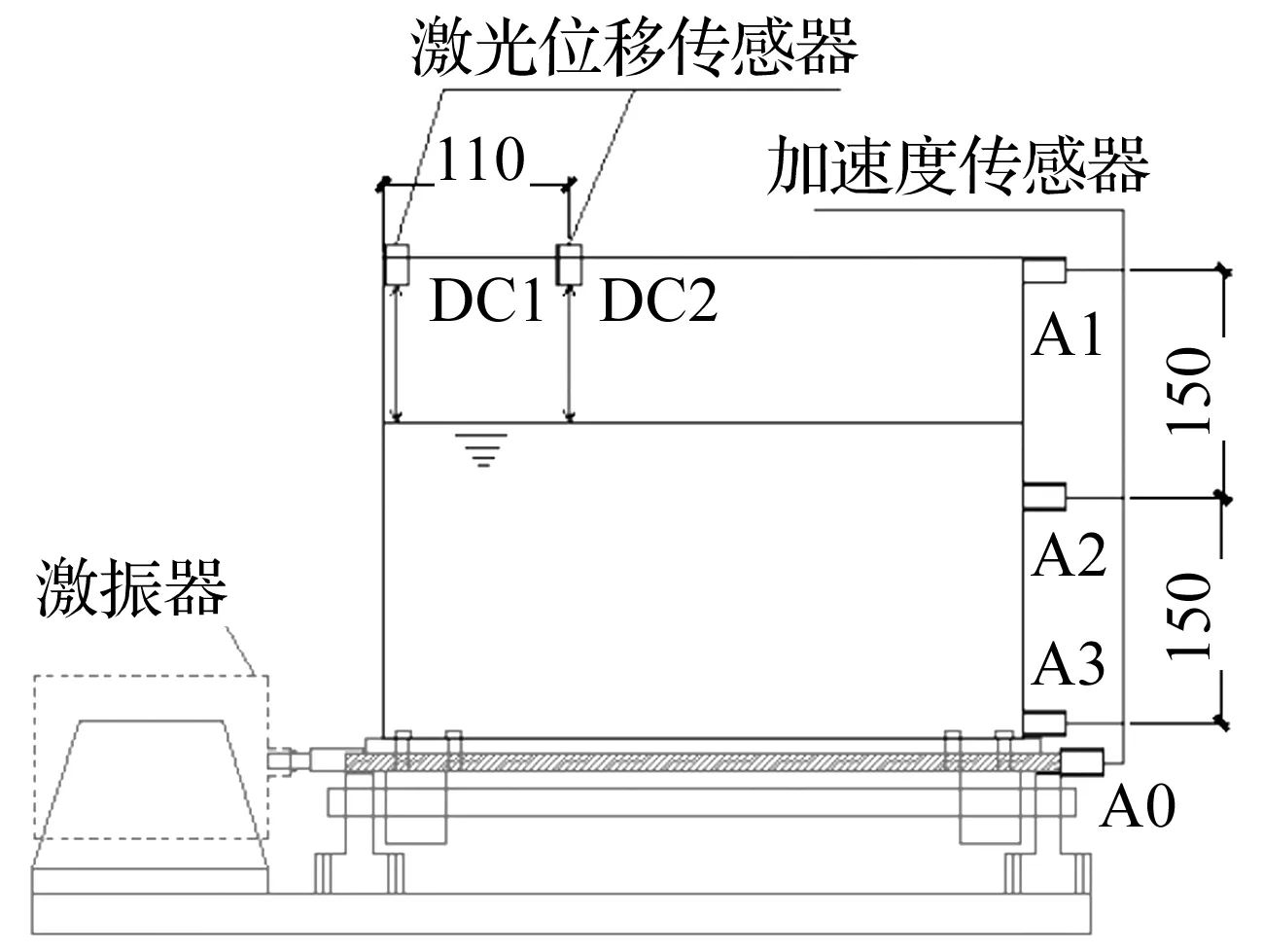
图2 加载装置与动力测试仪器布置图(mm)Fig.2 Diagram of the loading device (mm)

本文选用Northridge波作为外部激励，北岭大地震曾造成洛杉矶地区大规模的储油罐破坏[11]，因此对于储油罐的振动研究Northridge波比较有代表性，如图3所示。

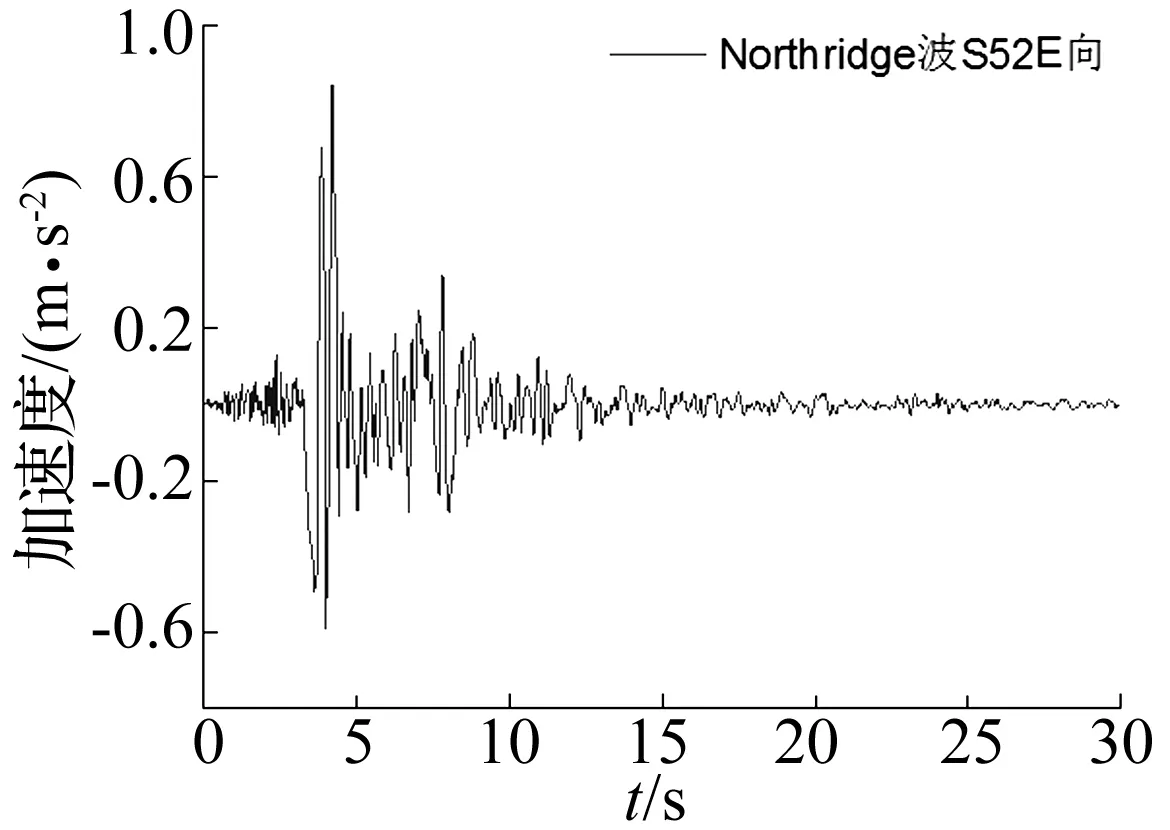
图3 Northridge波S52E向Fig.3 Northridge wave S52E

2 数值分析

2.1 计算理论与流固耦合机理

假定流体是均匀、无黏、无漩的理想流体，并限于讨论线性的小挠动情况，根据流体动力学理论可以推导出流体的运动方程式为：

(1)

与流体接触的结构的运动方程式为：

(2)

式中压力矢量p和系数矩阵B的定义与式(1)中的相同，可以看出式(1)是与式(2)耦合的。

可推导出结构-流体系统的运动方程式：

(3)

式中：r为位移矢量；p为压力矢量；ρ为液体密度；Ms为结构的质量矩阵；Cs为结构的阻尼矩阵；Ks为结构的刚度矩阵；fp为流固交界面上流体动力的节点矢量；f0为除了fp以外的其他外界激励矢量；q0为输入激励矢量，H、A、E、B为系数矩阵，如(4)式所示，其中N为形状函数。

(4)

由于减晃板可视作刚性，整个问题可简化为线性势流的自由晃动问题，相应的方程及边界条件如下：

(5)

结构-流体系统的运动方程可简化为：

(6)

由式(6)与式(3)的第二项系数对比可知，消去了系数A，使得流固耦合方程更加简单，易于求解。

有限元流固耦合机理如图4所示。

图4 流固耦合机理Fig.4 Fluid-structure interconnection mechanism

2.2 模型建立及求解

本文利用有限元分析软件ADINA，建立有、无减晃板储罐模型。为了便于对比仿真与试验结果，建立的有限元模型在尺寸、材料特性、边界条件等方面都与试验模型相一致。罐内液体选用势流体单元3D-FLUID来模拟。该单元基于势流理论，可以与ADINA软件中的结构单元耦合，结构的运动将使流体产生沿边界法向的相对运动，流体则对结构产生附加压力；并且该单元可以与压力边界条件耦合，该特点可以用于模拟自由液面，其流固耦合分析支持静力分析、瞬态分析和频域分析。由于储罐自身是由较薄的有机玻璃制成，符合壳单元的特性，所以罐体本身用SHELL弹性壳单元模拟[12]。为了更好地反应储罐在地震作用下罐身与液体的相互作用，模型考虑了储罐内部的液固耦合作用，采用直接耦合方法建立储罐的有限元模型，如图5所示。

图5 ADINA模型图Fig.5 ADINA model profile

2.3 模态分析

为了验证本文建模方法的可靠性，首先建立一个无环板的储液罐模型，进行模态分析，求出其结构自振特性，然后与规范解和试验解作对比验证。验证方法取得初步可行后，再进行储液罐在不同减晃板相对宽度、相对位置下的液体晃动特性和各项地震响应的对比分析。

由于储液晃动频率属于低频部分，而液固耦合的冲击频率属于高频部分，整个模态范围跨度较大。为了得到完整的模态变化，利用ADINA提取了前1 000阶模态，可以观察到储罐除了储液晃动和梁式振动外，还会发生周向cos(nθ)多波振型；cos(nθ)振型在圆周方向呈花瓣形，分布较广，前三阶振型如图6、图7所示。

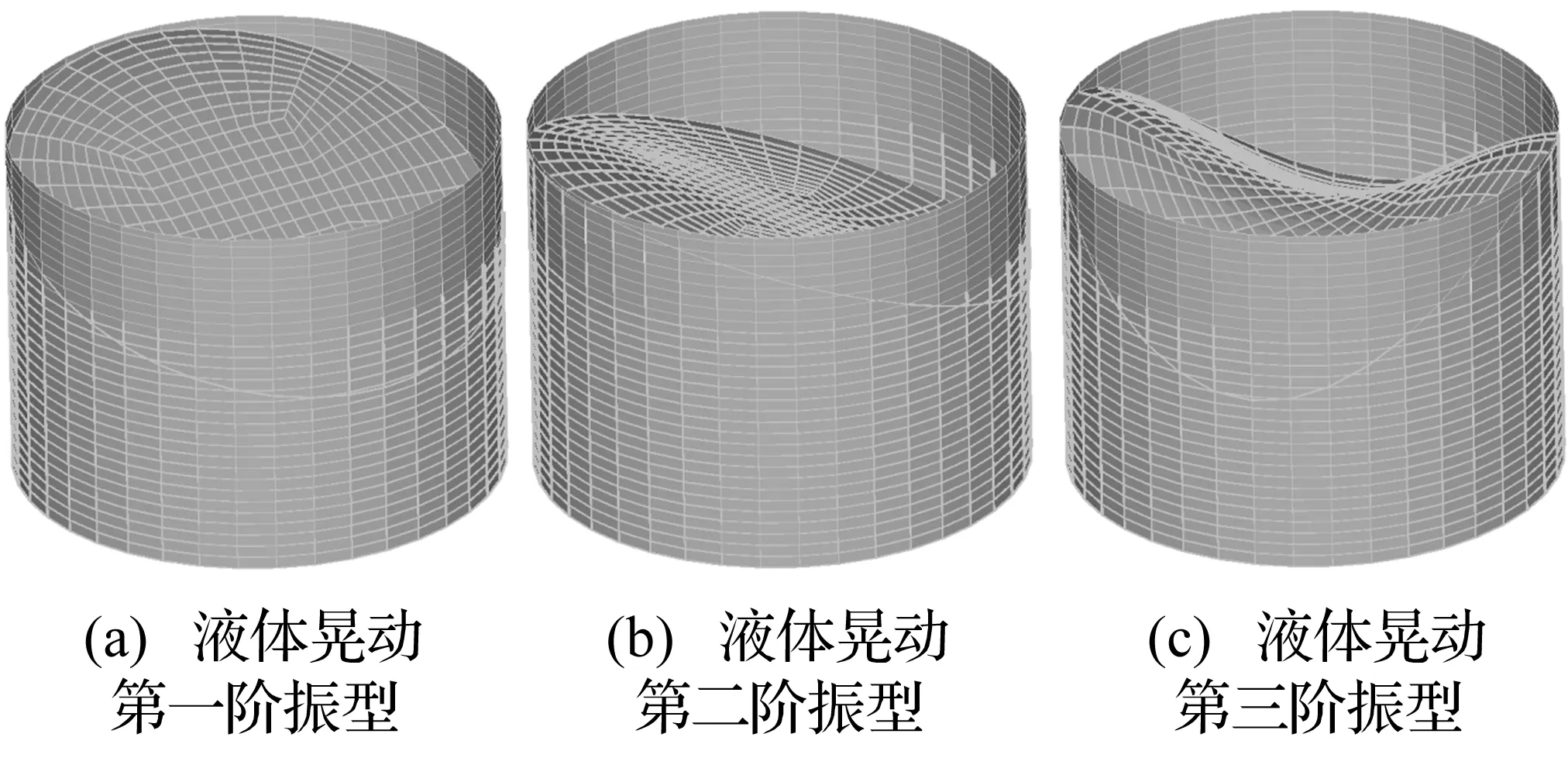
图6液体晃动前三阶振型Fig.6 The first three order sloshing modes

图7 液固耦合前三阶振型图Fig.7The first three order FSI modes

《立式圆筒形钢制焊接油罐设计规范》(GB 50341—2014)，提供了储罐罐液耦联振动基本周期与储液晃动基本周期的计算公式，规范计算结果与有限元分析结果的比较见表3。为了进一步证明有限元的可靠性,表3还列出了试验值,试验测得储液晃动周期为0.705 3 s,有限元解与试验解两者亦非常接近，说明了分析模型的可靠性。由于模型刚度较大，试验中并没有出现变形高阶模态，未能得到耦联振动周期。

表3 振动周期计算结果对比

注：Tc为耦联振动周期；Tw为储液晃动周期;其中3.7%为ADINA解与规范解的误差，7.9%为ADINA解与试验解的误差

3 结果对比分析

3.1 晃动波高

图8为减晃板不同相对宽度下的波高峰值的试验值和有限元模拟值。从图中可以看出减晃板对波高峰值起到了不同程度地控制效果；无减晃板时的储罐波峰试验值为80.7 mm，有限元模拟值为85.3 mm；有限元模拟值与与试验值比较接近，有限元值基本上都略微大于试验值，这是因为ADINA在采用势流体单元模拟液体时是把液体考虑成无黏、无漩的理想液体，这与试验所采用的水有略微差别，但是误差基本上在10%以内。

(a)相对宽度r/R=0.05 (b)相对宽度r/R=0.10 (c)相对宽度r/R=0.15 (d)相对宽度r/R=0.20图8 不同相对宽度下波高峰值Fig.8 Wave height amplitude of different relative width

为了更加直观的反映减晃板的减晃效果，定义波高衰减率为无减晃板与有减晃板波高峰值的差值与无减晃板波高峰值之比。

图9为不同相对宽度减晃板下波高衰减率试验值与有限元值的对比，由图中可以发现波高衰减范围在5%～60%之间，试验值与有限元值衰减趋势大致相同，都起到了良好的控制效果；另外试验和有限元值模拟都表明当减晃板相对深度在0.125～0.225且相对宽度在0.15～0.20之间时，减晃效果取得综合最优。

3.2 基底剪力

图10为不同减晃板相对宽度下储罐的基底剪力，由试验测得无减晃板时储罐的基底剪力峰值为152 N，对比图中试验值可知减晃板对储罐的基底剪力同样能起到了较好的控制效果，并且随着减晃板的布置位置不同基底剪力的控制效果差异较大；另外当减晃板相对宽度不大时，基底剪力基本上随着减晃板的布置深度地增加呈减小趋势，当相对位置处于0.125～0.225之间时，效果最优；但是当减晃板宽度达到一定宽度时，基底剪力会随着减晃板所处位置的加深呈现增大趋势，如图10(d)所示。根据HOUSNER[13]提出的质量-弹簧系统的模型，液面自由受水平激振，当罐壁为刚性时，将储罐液体视为两个不同模式下振动，其中底部部分液体像刚性附加质量一样与罐一起运动，其余液体则独立地做对流晃动，与罐壁同步运动的这部分液体质量即所谓“刚性冲击”质量部分，被晃动的那部分质量称为“对流”质量部分。当减晃板宽度在一定范围内时，对液体的竖向分割作用并不明显，此时减缓板所处的位置基本上在对流区域，主要对上部晃动、对流质量产生影响；但是当减晃板宽度达到一定宽度时，减晃板对液体的竖向分割作用明显，改变了两个不同模式下的质量分布，使得底部冲击质量部分增大，此部分对罐体的作用占罐体受力的主要部分，所以出现了图10(d)所示的曲线后段基底剪力上升的现象。

(a)相对宽度r/R=0.05 (b)相对宽度r/R=0.10 (c)相对宽度r/R=0.15 (d)相对宽度r/R=0.20图9 不同相对宽度下的波高衰减率Fig.9 Wave-height attenuation ratios of different relative width

(a)相对宽度r/R=0.05 (b)相对宽度r/R=0.10 (c)相对宽度r/R=0.15 (d)相对宽度r/R=0.20图10 不同相对宽度下的基底剪力Fig.10 Shear force of tank bottom under different relative width

图11为不同减晃板相对位置下储罐的基底剪力，由试验测得无减晃板时储罐的基底剪力峰值为152 N，对比图中试验值可知减晃板对储罐的基底剪力起到了较好的控制效果，并且随着减晃板相对宽度的不同，基底剪力的控制效果差异较大，但是当减晃板相对宽度在0.15附近时，减晃板对储罐基底剪力的控制效果比较理想。

(a) 相对位置h/H=1/15 (b) 相对位置h/H=1/5 (c) 相对位置h/H=4/15 图11 不同相对位置下的基底剪力Fig.11 Shear force of tank bottom under different relative location

3.3 罐壁应力

图12为无减晃板储罐的罐壁压应力峰值随着罐高的变化曲线。根据试验测得的三个高度处的罐壁压应力峰值可以发现接近罐底处的应力较大，这跟储罐容易在底部发生“象足”失稳破坏的部位相一致，这也说明储罐通常先发生靠近底部的失稳破坏，图中有限元值也证明了这一点。

图12 无减晃板罐壁应力峰值Fig.12 Pressure amplitude of tank wall without baffle

图13为减晃板为r/R=0.10、h/H=0时，储罐的罐壁应力峰值随罐高的变化。相对于图12无减晃板的罐壁应力峰值具有较大幅度的减小，这对减小罐壁底部发生“象足”屈曲的可能性具有积极意义。

图13 当r/R=0.10、h/H=0时罐壁应力峰值Fig.13 Pressure amplitude of r/R=0.10、h/H=0

4 结 论

(1)安装减晃板后，储罐内液体的晃动波高、罐底剪力及罐壁压应力等关键指标均有了明显的降低；抑制效果受减晃板宽度与布设位置等因素影响较大；当减晃板位于0.125 倍～0.225 倍的罐高位置且相对宽度在0.15附近时，抑制效果取得最优。

(2)晃动波高的显著降低，使得储液高度的限制得到了“解放”；相比无减晃板的罐体，带减晃板的储罐内液体的设计高度拥有了较大的提升空间，这对提高罐体储量和减小占地面积具有重要的现实意义。

(3)模型试验与仿真模拟均表明接近罐底处(“象足”型失稳破坏区)的罐壁易产生压应力峰值，而减晃设计后的储罐底部的罐壁压应力得到了显著的降低，可见本文的减晃设计能有效避免罐体发生“象足”失稳破坏。

[1] 立式圆筒形钢制焊接油罐设计规范:GB 50341—2014[S].北京：中国计划出版社，2014:82-83.

[2] HASHEMINEJAD S M,AGHABEIGI M. Sloshing characteristics in half-full horizontal elliptical tanks with vertical baffles[J]. Applied Mathematical Modelling, 2012,36(1): 57-71.

[3] ESWARAN M, SAHA U K, MAITY D. Effect of baffles on a partially filled cubic tank: numerical simulation and experimental validation[J].Comput Struct,2009，87:198-205.

[4] 王佳栋,周叮,刘伟庆. 水平激励下带环形刚性隔板圆柱形储液罐中流体的晃动响应[J]. 力学季刊,2011,32(2):166-172. WANG Jiadong, ZHOU Ding, LIU Weiqing. Sloshing response of liquid in cylindrical tank with a rigid annual baffle under horizontal loads[J].Chinese Quarterly of Mechanics,2011,32(2):166-172.

[5] BISWAL K C,BHATTACHARYYA S K,SINHA P K. Non-linear sloshing in partially liquid filled containers with baffles[J]. International Journal for Numerical Methods in Engineering, 2006,68(3): 317-337.

[6] 柳伟，周叮，刘伟庆,等. 基于概率密度演化的带有环形隔板圆柱形罐体中流体的晃动研究[J].振动与冲击，2015,34(11):110-115. LIU Wei, ZHOU Ding, LIU Weiqing, et al.Sloshing response of liquid in a cylindrical tank with an annual baffle based on probability density evolution theory[J].Journal of Vibration and Shock,2015,34(11):110-115.

[7] AKYILDIZ H,ERDEMÜNAL N, AKSOY H. An experimental investigation of the effects of the ring baffles on liquid sloshing in a rigid cylindrical tank[J]. Ocean Engineering, 2013,59: 190-197.

[8] AKYILDIZ H, UNAL N E. Experimental investigation of pressure distribution on a rectangular tank due to the liquid sloshing[J]. Ocean Engineering, 2005, 32(11/12)：1503-1516.

[9] AKYILDIZ H, UNAL N E. Sloshing in a three-dimensional rectangular tank：numerical simulation and experimental validation[J]. Ocean Engineering, 2006, 33(16)：2135-2149.

[10] 孙建刚. 大型立式储罐隔震——理论、方法及实验[M].北京：科学出版社，2010:214-215.

[11] 李扬. 基础隔震储罐地震反应与控制研究[D].青岛：中国石油大学(华东)，2009:1-2.

[12] 马野，袁志丹，曹金凤.ADINA有限元经典实例分析[M].北京：机械工业出版社，2011．

[13] HOUSNER G W. Dynamic pressure on accelerated fluidcontainers[J]. Bulletin of Seismological Society of America,1957,47(1):15-35.

Experimental study and finite element analysis on the sloshing suppression in storage tank under seismic excitations

QI Yongcheng, QIU Hongxing, MA Yongquan

(College of Civil Engineering, Southeast University, Nanjing 210096, China)

Focusing on the suppression of liquid sloshing which may cause the elephant-foot buckling of storage tank walls, ring baffles were taken as a suppression device and its optimization design was carried out. An experimental research and a finite element analysis were performed on a 1∶30 reduced-scale model. By using the model with or without baffles, the wave height, base shear force and tank wall pressure in both cases were investigated and compared. The reliability of the finite element simulation was verified by comparing the numerical results with the experimental ones. The study shows when the distance from liquid surface to the location of baffles relative to tank height is 0.125-0.225 and the baffle width relative to tank radius is near 0.15, the effect on suppressing wave is the most remarkable, additionally, near the bottom of tank, the stress reaches the maximum peak, which indicates the bottom region is just the elephant-foot buckling area. Thsi is of guiding significance for preventing failures.

vertical storage tank; seismic excitation; ring baffles; model experiment; finite element

国家十二五科技支撑计划项目(2012BAJ14B02)

2015-06-10 修改稿收到日期：2015-12-20

祁永成 男，硕士生，1990年生

邱洪兴 男，博士，教授，博士生导师，1962年生 E-mail:qiuhx@seu.edu.cn

TU279.7; TU352.1

A

10.13465/j.cnki.jvs.2017.02.031