椭圆形泡沫填充薄壁管斜向冲击吸能特性仿真研究

高 强， 王良模， 王源隆， 王 陶， 郭福祥， 张遵智

(1.南京理工大学 机械工程学院，南京 210094； 2.南京依维柯汽车有限公司，南京 210028)

椭圆形泡沫填充薄壁管斜向冲击吸能特性仿真研究

高 强1， 王良模1， 王源隆1， 王 陶1， 郭福祥2， 张遵智2

(1.南京理工大学 机械工程学院，南京 210094； 2.南京依维柯汽车有限公司，南京 210028)

为了提高汽车在斜向碰撞中的防撞性，提出了一种新型的椭圆形泡沫填充管。以比吸能和冲击力峰值作为评价指标，采用有限元仿真的方法分析了椭圆向心率、壁厚和泡沫铝密度等参数对其斜向冲击吸能特性的影响。结果表明：向心率的减小 ，在小角度冲击时，可降低冲击力峰值，大角度冲击时，能提高比吸能量；比吸能和冲击力峰值与壁厚近似为线性关系；泡沫铝密度为0.153 g/cm3时，泡沫填充管的综合比吸能最小，而冲击力峰值则随着泡沫密度的增大而增大。因此，合理地设计椭圆形泡沫填充管参数有利于提高汽车的防撞性，从而提高乘员安全性能。

泡沫填充管；耐撞性；吸能；斜向冲击

汽车安全性越来越受到人们的重视，外很多学者研究了薄壁管在轴向冲击和斜冲击下的特性，也取得了很多的成就。侯淑娟[1]提出双层吸能结构以及组合型吸能结构来代替传统的单层薄壁管，在防撞性能上有显著的提高；唐智亮[3]则对仿生非凸薄壁管、多胞结构薄壁管以及圆柱夹层多胞结构的薄壁管的吸能特性进行了相关的仿真研究并通过试验加以验证；张雄[4]研究了不同截面形状对薄壁管防撞性能的影响，发现截面形状的角越多，越利于能量的吸收，直至截面形状趋近于圆，但是圆的冲击力频率较大，吸能不够稳定；张宗华[5]对蜂窝夹芯结构以及S型纵梁的轴向冲击进行了数值模拟；HASSEN等[6]总结出圆形截面与方形截面的空心薄壁管与泡沫填充管在轴向准静态力和冲击下的平均力公式，并通过相关的实验进行验证，这对于后面学者建立有限元模型和模型正确性的验证具有重要的指导作用。YIN等[7-9]提出泡沫填充管，除了空心薄壁管与泡沫铝的吸能作用外，薄壁管与泡沫铝在冲击作用下，相互作用，从而提高了比吸能量，证明了泡沫填充管比空心薄壁管具有更好的吸能特性，在实际工程中已有很多的应用。

考虑到汽车实际碰撞过程中有正面碰撞也有斜向碰撞，而薄壁管在斜向冲击中的特性与轴向冲击的吸能特性差异很大，因此分析薄壁管在斜向冲击下的防撞特性就很有必要。YIN等[10]提出了梯度泡沫密度填充管，利用泡沫密度的变化来充分利用材料的变形吸收更多的能量，并进行了相关的优化分析；ZHANG等[11]对变厚度的圆锥管的斜向冲击性能进行了详细的研究，发现其在斜向冲击中的防撞特性是优于普通圆柱薄壁管；QI等[12]则分析了锥形方形多胞薄壁管在不同斜向冲击角度下的特性，并与普通方形截面的锥形薄壁管进行了对比，表明多胞管在斜向冲击下都有优于普通薄壁管的防撞性能。DJAMALUDDIN等[13]研究了泡沫填充的双圆管结构在斜向冲击下的优越性，并采用优化算法对其结构进行了优化。ALI等将正交试验，代理模型引入到薄壁管的研究中，大量的节省了薄壁管试验的次数，以及有限元模型的运算，在保证精度的前提下，极大地提高了研究效率。在薄壁管件的参数优化方面，智能优化算法，如种群粒子算法，改进的遗传算法也被广泛的应用。

基于以上研究，本文提出了一种新型的椭圆形截面的泡沫填充管，在冲击角度为0°，10°，20°，30°下吸能特性较为稳定，且比吸能高，冲击力峰值低的特性，通过有限元的方法进行分析，以比吸能以及冲击力峰值为评价指标，分析了影响椭圆形泡沫填充管自身参数对其防撞性的影响。研究表明在参数匹配得当时，椭圆形泡沫填充管防撞性优越，具有一定的应用前景。

1 问题描述

1.1 斜向冲击下的耐撞性指标

通常情况下，表征结构吸能特性及耐撞特性的有以下指标：结构总吸收冲击能量(EA)，整体结构单位质量吸收的冲击能量，即比吸能(SEA)，平均碰撞力(MCF),碰撞力峰值(PCF)。EA是结构整个碰撞过程中吸收的能量，表征为

(1)

式中:d为结构在冲击载荷下的变形长度。根据文献[3]，本文中结构的有效变形量取其总长的 70%。结构单位质量的吸能量SEA表征为

(2)

式中:M为结构的总质量，E为结构吸收的总冲击能量。

平均碰撞力(MCF)是碰撞力在整个碰撞过程中的平均值，表征为

(3)

式中：d为结构在碰撞过程中的有效压缩距离。

碰撞力峰值(PCF)是在整个碰撞过程中的最大的碰撞力，表征为

PCF=max[F(d)]

(4)

式中：F(d)是压缩距离为d时的碰撞力的大小。碰撞峰值力通常出现在：①结构刚发生屈曲破坏时，即临界失稳，通常由结构的弹塑性屈曲决定；②结构被压实阶段(密实化)阶段，此时碰撞力会迅速增大。

考虑斜向冲击角度对结构吸收能量和碰撞力峰值的影响，定义斜向冲击下的综合比吸能：

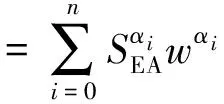
(5)

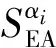
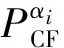
(6)

式中:PCFα为综合的冲击峰值力。

1.2 物理模型

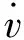
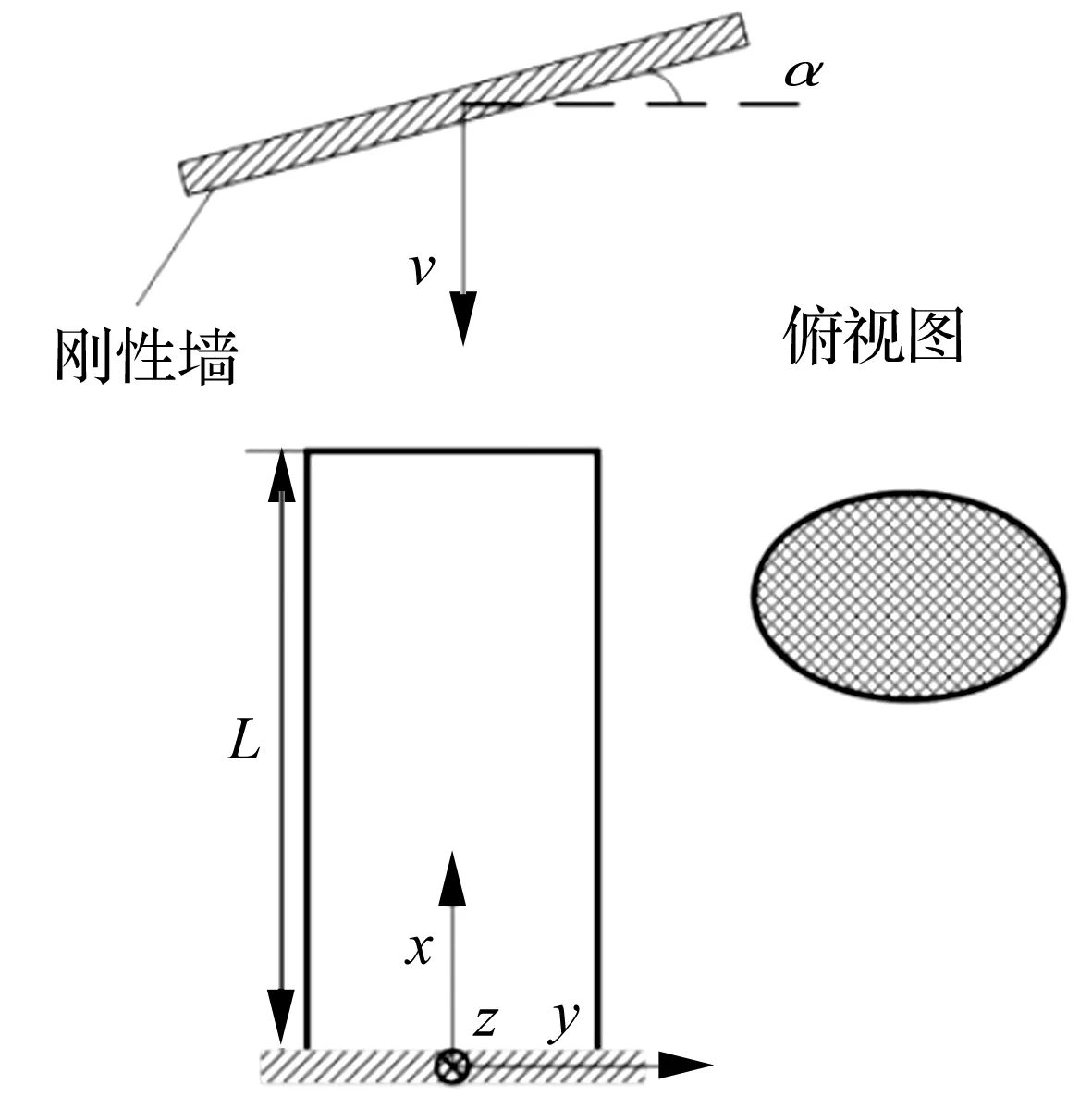
图1 椭圆泡沫填充管斜向冲击示意图Fig.1 Schematic diagram of foam-filled oval tube under oblique impact

1.3 椭圆的几何描述

本文研究的对象是椭圆泡沫填充直管，如图2所示，椭圆的长半轴长为a，短半轴长为b，F1为椭圆焦点，c为焦距的一半，向心率为f，计算如式(7)。

f=b/a

(7)

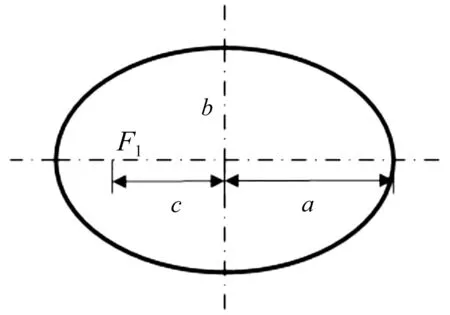
图2 椭圆参数示意图Fig.2 Schematic diagram of oval tube parameter

2 有限元建模与模型验证

2.1 椭圆管几何与材料参数

管壁采用 AA6060-T4 铝合金材料，密度ρ=2 700 kg /m3，杨氏模量E=68.2 GPa，泊松比v=0.3，屈服应力σy=80 Mpa，极限应力σu=173 Mpa，幂指强化系数n=0.23，延伸率ε=17.4%。应力-应变曲线如图3所示。由于铝合金材料对应变率不敏感，建模时不考虑应变率对材料参数的影响。

由Hydro Aluminium AS公司生产铝泡沫材料被Hassen等广泛应用到相关研究中，这里采用Despande和Fleck提出的各向同性本构模型来模拟这种泡沫。根据这一模型，泡沫材料的屈服函数定义：

(8)

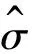
(9)

σe是等效应力von Mises应力，σm是平均应力，参数α控制着屈服面的形状，它是塑性泊松比νp的函数，定义为

(10)

材料模型遵循下面的应变强化规律：

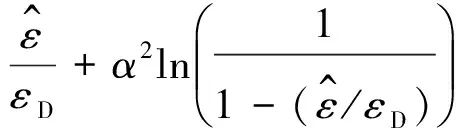
(11)

(12)

式中：ρf是泡沫的密度，ρf0是泡沫基准材料的密度。根据文献[4]，铝泡沫材料的塑性泊松比vp取值0.02～0.17之间，在本文中对于所有密度的泡沫均取为0.1，其它材料参数列于表1中。

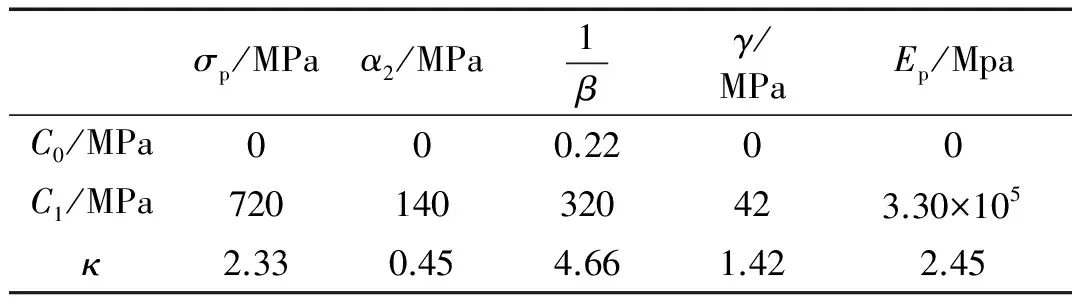
表1 泡沫铝的材料参数

2.2 有限元建模

利用有限元前处理软件 HYPERMESH 建立的椭圆形泡沫填充管有限元模型如图4，椭圆形薄壁管采用适合于大变形分析的 Belytschko-Tsay 四节点薄壳单元建模，考虑到仿真精度和求解效率的要求，薄壳单元沿厚度方向取 3个积分点，面内采用缩减积分。泡沫材料采用8节点实体单元模拟，所有单元为六面体单元。壳单元和实体单元的特征长度分别取2.5 mm和4 mm。管壁材料 AA6060-T4采用LS-DYNA 中 #123 号材料模型 modified piecewise linear plasticity建模，铝泡沫材料采用#154 Despande Fleck foam材料模型模拟。

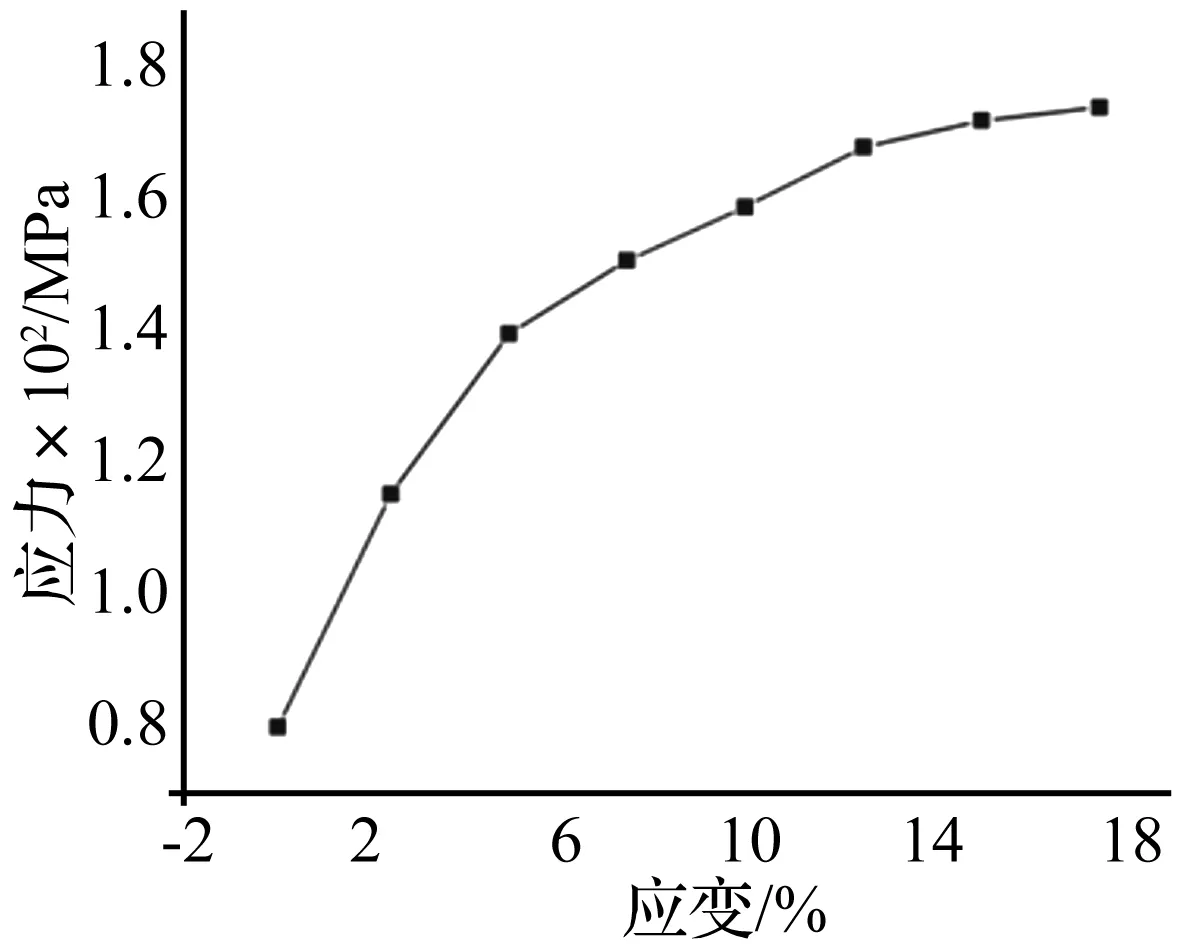
图3 应力应变曲线( AA6060-T4 铝合金材料)Fig.3 Tensile stress-strain curve of AA6060 T4

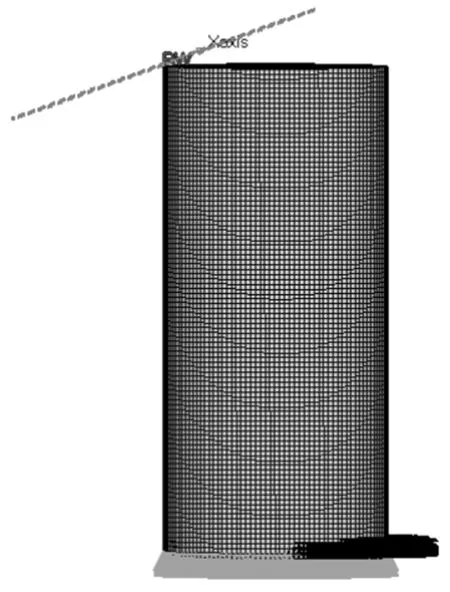
图4 有限元模型Fig.4 Finite element model

在泡沫填充管的分析过程中共采用四类接触条件：对管壁采用自动单面接触( automatic single-surface contact )算法，以考虑压缩过程中管壁自身变形可能产生的接触；管壁与泡沫材料之间采用自动面面接触(automatic surface-to-surface contact)管壁与刚性板以及泡沫与刚性板之间采用自动点面接触(automatic node-to-surface contact)。此外，为了防止泡沫在加载过程中出现数值问题(负体积问题)，对泡沫单元施加了内部接触(contact interior)算法。计算中同时考虑管与刚性墙之间的摩擦以及管自身的摩擦作用，面与面间的静、动摩擦因数均取0.2。结构底部节点施加所有六个自由度的位移约束以模拟固支边界条件。刚性墙的形状、方向和速度通过关键字RIGID WALL_GEOMETRIC_FLAT_MOTION 定义。

2.3 有限元模型验证

为了验证所建立的椭圆型管与椭圆泡沫填充管模型的准确性，由于没有相关的的椭圆形的相关实验，取与之类似的圆形薄壁管及泡沫填充管进行验证。首先根据WIERZBICKI等提出圆形薄壁管的平均力公式(13)。

(13)

式中：κD是表征在不同加载情况下的常数；σ0是壁管的流体应力；bm是管壁内截面宽度，t是管壁厚度。HANSSEN等研究出泡沫填充管的平均力相关表达式，如式(14)。

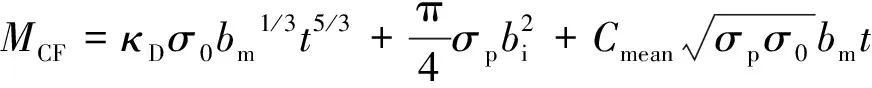
式中：bi表示泡沫核的宽度，σp表示泡沫的屈服应力，泡沫与管壁的相互作用常数为Cmean，其与圆管直径与长度的比值DC关系如式(15)。

Cmean=2.78×DC+1.29

(15)

根据文献[13]选取直径为80 mm，长度230 mm，厚度不同的模型进行验证。理论与有限元的建模对比如表2。表中建立的模型与理论的平均力的误差均是小于5%,这在工程中是允许的。再者，根据文献[14]所建立的模型进行仿真，与其实验结果进行对比，如图5所示，变形模式和最终的变形结果均很相似，也验证了模型的准确性，为下文的分析打下基础。

图5 试验与仿真模型对比Fig.5 Comparison of experiment and simulation model

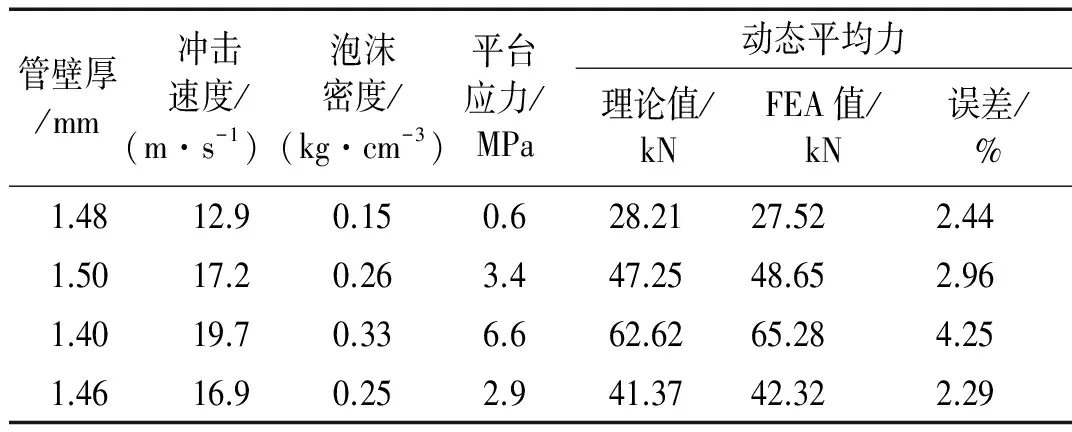
管壁厚/mm冲击速度/(m·s-1) 泡沫密度/(kg·cm-3)平台应力/MPa动态平均力理论值/kNFEA值/kN误差/%1．4812．90．150．628．2127．522．441．5017．20．263．447．2548．652．961．4019．70．336．662．6265．284．251．4616．90．252．941．3742．322．29

综上所述，可以认为本文所采用的建模方法以及参数设置是有效的，与实际情况较为符合。

3 结构参数对椭圆形泡沫铝填充管的防撞性的影响

椭圆形泡沫填充管的防撞性能与其本身的结构参数息息相关，因此选取椭圆的向心率f，薄壁管壁厚t，泡沫密度ρf这3组参数进行分析，相关参数变化如表3所示。以长度为250 mm，壁厚为2 mm，管壁材料AA6060-T4铝合金材料，泡沫密度取0.206 g/cm3的薄壁管为基础模型。刚性墙的压缩速度v=10 m/s，压缩距离为薄壁管长度的70%。

图6是椭圆形泡沫填管在冲击角度为 0° ，10°，20°，30°时的变形模式。

图6 椭圆形泡沫填充管的变形模式Fig.6 Deformation mode of the foam-filled tube

3.1 向心率的影响

在基准模型的基础上保持壁厚以及泡沫密度不变，分析不同的向心率的模型，分析其对斜向冲击防撞性能的影响。向心率对比吸能量，冲击力峰值的影响如图7和图8所示。不同向心率的模型的综合比吸能量如图9所示。

图7表明，在轴向和小角度冲击下，向心率的比吸能基本相近，随着冲击力角度的增大，在大角度冲击下，向心率越小，比吸能越大，且不同的向心率所产生的比吸能差的趋势也更明显，体现出椭圆形薄壁管在大角度冲击下防撞性的优越。这是因为在大角度的斜向冲击中，向心率小的椭圆有更多的材料参与到变形吸能中，且长半轴的增长有利于减小斜向冲击中管壁的受力力矩，故向心率小的椭圆模型在大角度有更好的防撞性能。各个向心率的模型的比吸能均随着冲击的角度增大而减小，在0°～20°之间变化急剧。

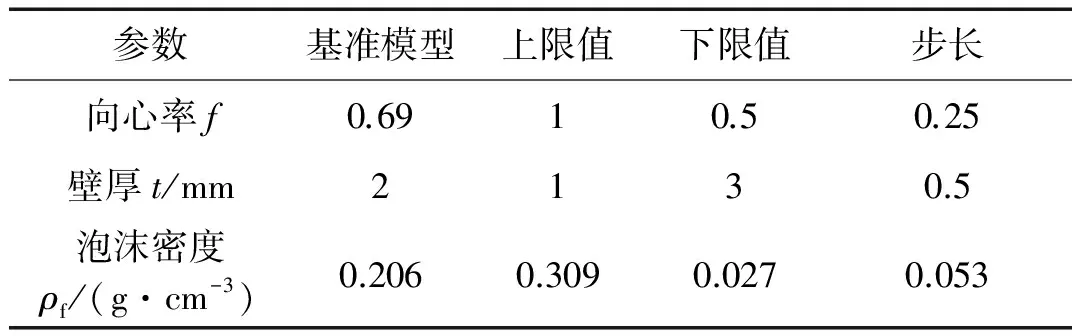
表3 椭圆形泡沫填充管的参数取值

图8则表明，在小角度的冲击下，冲击力峰值随着向心率的增大而增大。而当冲击角度达到30°时，向心率对冲击力峰值影响不大，综合考虑，较小向心率的椭圆的冲击力峰值较小，更加利于乘员的保护。

图9表明：在考虑了0°，10°，20°，30°四种冲击角度的比吸能情况下，向心率对综合比吸能的影响并不是单调的，向心率为0.625的薄壁管综合比吸能最大。这是在4种冲击角度的加权比重均为0.25时所产生的结果，而在取不同加权比重指标时，所得的结果将会有所不同。

图7 向心率对比吸能的影响Fig.7 Effect of radial rate on SEA under oblique impact

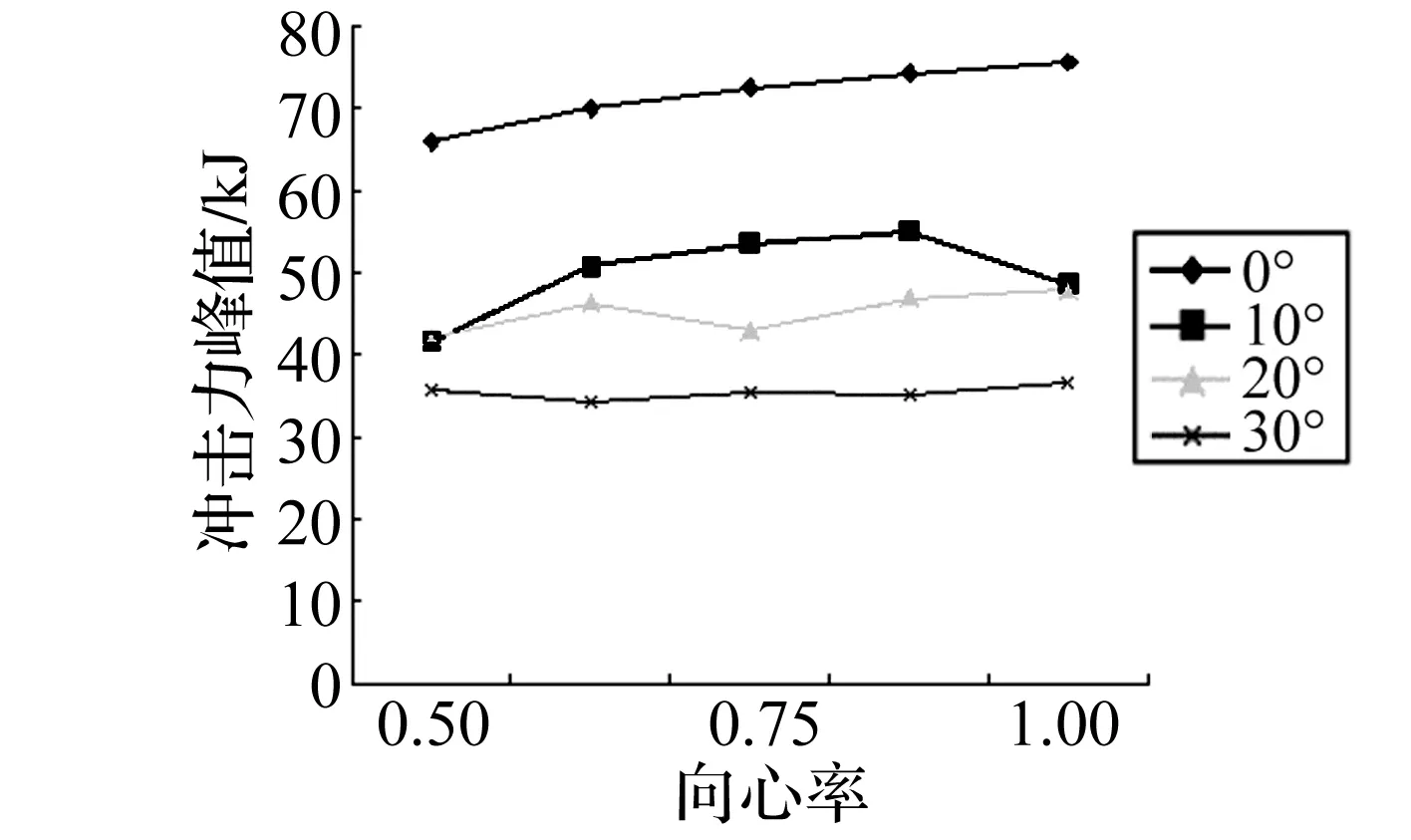
图8 向心率对冲击力峰值的影响Fig.8 Effect of radial rate on PCF under oblique impact

图9 不同向心率下的综合比吸能Fig.9 SEAa of oval tubes of different radial rate under oblique impact

3.2 壁厚的影响

壁厚是影响薄壁管斜向冲击刚度的重要因素。如图10，可知在轴向以及小角度冲击中，壁厚的增大对于增加薄壁管的比吸能效果显著，而随着冲击角度的增大，壁厚的增加对于比吸能的效果随之减弱，也就是说壁厚越大，薄壁管对于冲击角度的越敏感。这是由于壁厚越小，薄壁管件刚度越小，在大角度冲击下，受载端更容易发生屈服，溃缩，从而吸收能量。而壁厚较大的薄壁管件刚度较大，更早地进入整体弯曲吸能的模式，从而减少了能量的吸收。

图10 壁厚对比吸能的影响Fig.10 Effect of wall thickness on SEA under oblique impact

图11则显示了不同壁厚的薄壁管在不同冲击力角度下的冲击力峰值的情况。无论何种壁厚的薄壁管件，冲击力峰值均随着冲击力角度的增大而减小，壁厚越大的薄壁管冲击力峰值随着角度的增大变化越显著，但是壁厚为2.5 mm时，轴向的冲击力峰值已达到90 kN左右，尽管壁厚的增加有助于比吸能的增大，但过大的冲击力峰值，会使整车碰撞时加速度的上升，从而不利于乘员保护。因此，选择合适的壁厚对于乘员的保护至关重要。

图11 壁厚对冲击力峰值的影响Fig.11 Effect of wall thickness on PCF under oblique impact

3.3 泡沫密度的影响

不同泡沫铝密度对防撞性能也有着极其重要的影响，它直接影响着泡沫铝的吸能特性以及泡沫铝与薄壁管的相互作用，从而改变薄壁管的屈曲波长和屈曲载荷。不同密度泡沫铝的比吸能与冲击力峰值如图12,13所示。

图12表明：泡沫密度对比吸能的影响并不是单调的，而是在每个角度下，都存在一个泡沫密度对应的比吸能最小，而且在不同角度下的对应比吸能最小的泡沫铝密度不尽相同。在0°，10°冲击力下，泡沫密度为0.103 g/cm3时比吸能最小，而在20°，30°冲击下，泡沫密度为0.153 g/cm3时比吸能最小。可知随着角度的增大，最小比吸能值的所对应的泡沫铝密度在增大。而对比综合比吸能值(图13)时，可以得出泡沫密度为0.153 g/cm3时比吸能最小，在此基础上，泡沫铝密度的增大或减小均能提高管件的比吸能值。

图12 泡沫密度对比吸能的影响Fig.12 Effect of foam density on SEA under oblique impact

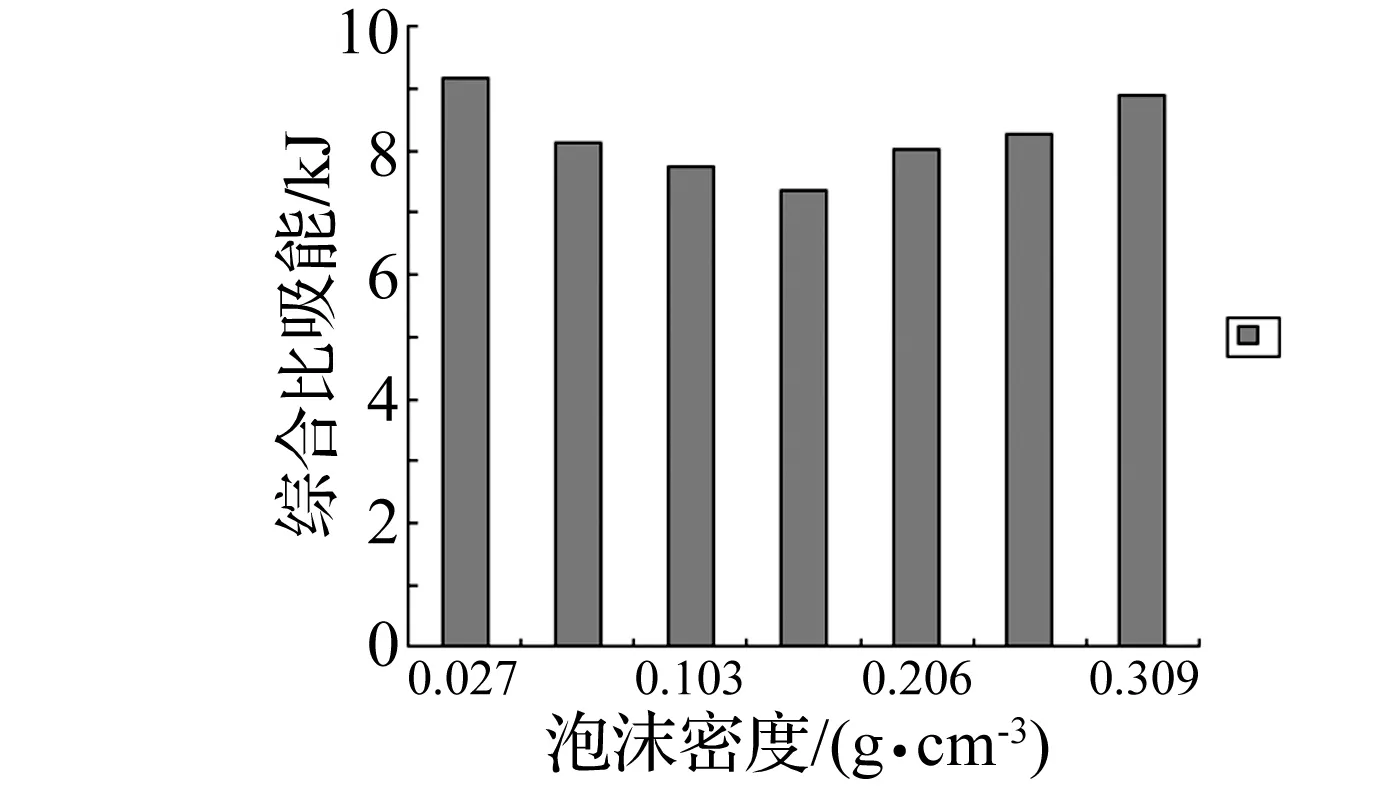
图13 各泡沫密度下的综合比吸能Fig.13 SEAa of oval tubs of different foam density under oblique impact

图14表明：无论在何种冲击角度下，随着泡沫铝的密度的增加，冲击力峰值也会随之增大，因此必须将泡沫铝的密度控制在一定范围内，以防止冲击力峰值过大而影响乘员的安全保护。

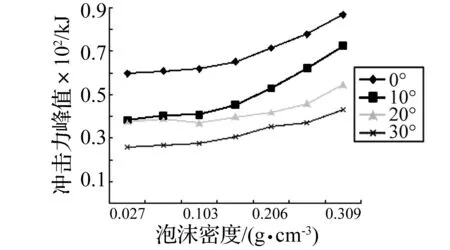
图14 泡沫密度对冲击力峰值的影响Fig.14 Effect of foam density on PCF under oblique impact

4 结 论

本文提出了一种新型的椭圆形泡沫铝填充薄壁管，运用LS_DYNA仿真研究椭圆形泡沫填充薄壁管向心率，壁厚和泡沫铝密度对其冲击性能的影响。通过研究得到以下结论：

(1)椭圆截面的向心率对其防撞性的影响在不同冲击角度下也不尽相同。在小角度冲击下，向心率对其比吸能影响不大，冲击力峰值则随着向心率的增大而略有增加；在较大角度冲击下，向心率的减小会增大比吸能量，且冲击角度越大，对比吸能的影响越明显，冲击力峰值则几乎不受向心率的影响。

(2)薄壁管的壁厚与比吸能和冲击力峰值的近似为线性关系，比吸能和冲击力峰值均随着壁厚的增加而增加，且在小角度情况下，变化更为显著。

(3)泡沫铝的密度的增大会直接增加冲击力峰值；对于比吸能而言，存在一个特定的泡沫铝密度值，当泡沫铝在此基础上增大或减小其密度时，都会增大比吸能量。

总体看来，椭圆形泡沫铝结构是一种斜向冲击下防撞性能优越的新型结构。本身参数对其的影响，可以通过相应的数值优化来达到所需要的最优结构。

[1] 侯淑娟. 薄壁构件的抗撞性优化设计[D]. 长沙: 湖南大学, 2007.

[2] 董喜文. 金属薄壁管的耐撞性优化设计[D]. 成都: 西南交通大学, 2014.

[3] 唐智亮. 薄壁结构轴向冲击能量吸收性能分析与改进设计[D]. 大连: 大连理工大学, 2012.

[4] 张雄. 轻质薄壁结构耐撞性分析与设计优化[D]. 大连: 大连理工大学, 2008.

[5] 张宗华. 轻质吸能材料和结构的耐撞性分析与设计优化[D]. 大连: 大连理工大学, 2010.

[6] HANSSEN A G, LANGSETH M, HOPPERSTAD O S. Static and dynamic crushing of circular aluminium extrusions with aluminium foam filler [J]. International Journal of Impact Engineering, 2000, 24: 475-507.

[7] YIN H, XIAO Y, WEN G, et al. Multiobjective optimization for foam-filled multi-cell thin-walled structures under lateral impact [J]. Thin-Walled Structures, 2015, 94: 1-12.

[8] ZAREI H R, KRÖGER M. Optimization of the foam-filled aluminum tubes for crush box application [J]. Thin-Walled Structures,2008, 46(2): 214-221.

[9] ALI M, OHIOMA E, KRAFT F, et al. Theoretical, numerical, and experimental study of dynamic axial crushing of thin walled pentagon and cross-shape tubes[J]. Thin-Walled Structures, 2015, 94: 253-272.

[10] YIN H, WEN G, WU X, et al. Crashworthiness design of functionally graded foam-filled multi-cell thin-walled structures [J]. Thin-Walled Structures,2014, 85: 142-155.

[11] ZHANG X, ZHANG H. Relative merits of conical tubes with graded thickness subjected to oblique impact loads [J]. International Journal of Mechanical Sciences,2015, 98: 111-125.

[12] QI C, YANG S, DONG F L. Crushing analysis and multiobjective crashworthiness optimization of tapered square tubes under oblique impact loading[J]. Thin-Walled Structures, 2012, 59: 103-119.

[13] DJAMALUDDIN F, ABDULLAH S, ARIFFIN A K, et al. Optimization of foam-filled double circular tubes under axial and oblique impact loading conditions. [J]. Thin-Walled Structures,2014, 78: 327-335.

[14] ZHANG Y, SUN G, XU X, et al. Multiobjective crashworthiness optimization of hollow and conical tubes for multiple load cases [J]. Thin-Walled Structures,2014, 82: 331-342.

[15] LI G, ZHANG Z, SUN G, et al. Comparison of functionally-graded structures under multiple loading angles [J]. Thin-Walled Structures,2015, 94: 334-347.

Energy-absorbing characteristics of foam-filled oval tubes under oblique impact

GAO Qiang1, WANG Liangmo1, WANG Yuanlong1, WANG Tao2, GUO Fuxiang2, ZHANG Zunzhi2

(1. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2. Nanjing Iveco Automobile Co. Ltd., Nanjing 210028, China)

In order to improve the crashworthiness of the vehicles under oblique collision, a novel foam-filled oval tube was proposed. The specific energy absorption (SEA) and peak crushing force (PCF) were adopted as crashworthiness indices. Then a finite element simulation was used to analyze the effects of structural parameters, including the oval radial rate, wall thickness and foam density on the energy-absorbing characteristics of the tube. The results show that:with the reduction of radial rate, the PCF increases under small angle impact and SEA increases under large angle impact. Besides, the SEA and PCF are approximately linear with the wall thickness. When the density of foamed aluminum is 0.153 g/cm3, the composite SEA of the foam filled tube reaches minimum, and the PCF increases with the increase of foam density. It is advantageous to improve the automobile’s crashworthiness and safety performance by reasonably designing the parameters of foam-filled oval tubes.

foam-filled tube; crashworthiness; energy absorption; oblique impact

江苏省产学研联合创新资金(BY2014004-04);南京市产学研项目(201306011)

2015-09-09 修改稿收到日期：2015-12-30

高强 男，博士，1991年10月生

王良模 男，博士，教授，1963年8月生 E-mail:liangmo@mail.njust.edu.cn

TB332

A

10.13465/j.cnki.jvs.2017.02.033