钢筋混凝土直螺栓管片接头抗弯极限承载力的简化计算模型
李守巨, 刘军豪, 上官子昌, 于 申
(1. 大连理工大学工业装备结构分析国家重点实验室, 辽宁 大连 116024;2. 大连海洋大学海洋与土木工程学院, 辽宁 大连 116023)
钢筋混凝土直螺栓管片接头抗弯极限承载力的简化计算模型
李守巨1, 刘军豪1, 上官子昌2, 于 申1
(1. 大连理工大学工业装备结构分析国家重点实验室, 辽宁 大连 116024;2. 大连海洋大学海洋与土木工程学院, 辽宁 大连 116023)
为了研究盾构隧道混凝土管片中轴力对接头极限弯矩的影响,将螺栓连接的混凝土管片接头简化成梁模型,建立混凝土管片接头极限承载力的计算模型。基于弯矩作用下管片接头截面平面变形假定,推导管片接头截面力平衡和弯矩平衡表达式,建立受拉区螺栓应力与受压区高度和混凝土极限应变之间的关系。以北京地铁隧道和上海地铁隧道管片为例,分析轴力对混凝土管片接头极限承载力的影响,并研究管片接头的破坏方式。研究表明,地铁隧道管片接头的极限承载力随着轴力的增加而增加,将解析模型计算结果与有限元模型结果进行对比,验证了所提出计算模型的准确性。
盾构隧道; 极限弯矩; 螺栓; 混凝土管片; 极限承载力
0 引言
盾构法是暗挖法施工中的一种全机械化施工方法,它是将盾构机械在地下推进,通过盾构外壳和管片支撑四周围岩防止隧道内坍塌,同时在开挖面前方用切削装置进行土体开挖,通过出土机械运出洞外,靠千斤顶在后部加压顶进,并拼装预制混凝土管片,形成隧道结构的一种机械化施工方法。盾构隧道由于施工方便、高效、安全等特点,逐渐被应用到地铁、公路和铁路工程中。由于盾构管片的应用日趋普遍,盾构管片结构的力学计算模型及其研究也越来越多。Mashimo等[1]通过实地测量,对盾构隧道衬砌荷载计算公式进行了准确性评估;CAO等[2]通过多尺度建模的方法模拟输水隧道的力学特性; ZHANG等[3]分别用有限元和四点弯曲试验研究复合管片的力学行为;Moller等[4]和Do等[5]进行2D有限元分析,并且前者对盾构隧道的施工步骤提出了改进方法;CHEN等[6]建立了隧道管片的三维有限元模型,并对其在不同外力作用下的开裂破损情况进行了研究。盾构隧道的衬砌结构由预制管片拼接安装而成,在管片的接头部位主要连接形式为螺栓连接,由此将产生大量相对于混凝土管片刚度较低的接缝,这些接缝严重影响衬砌的受力和变形,将影响整个结构的承载能力和安全性能。因此,对混凝土管片接头的力学特性进行研究就显得十分重要。已有很多学者对盾构管片接头部分的重要性和复杂性进行了分析研究。张厚美等[7-8]对直螺栓和弯螺栓接头进行了足尺抗弯试验,并将衬垫看作弹簧,提出管片接头刚度计算方法,得出螺栓的形式对接头力学性能影响不大的结论;黄钟晖[9]假定混凝土受压区压力分布为二次抛物线,推导了接头受压区高度的计算方法,并用有限元模拟进行验证;董新平等[10-11]建立接触面缺陷模型,并给出接头抗弯破坏历程中几个阶段的解析解,但研究中并未考虑螺栓的作用;SONG等[12]用简化的梁-弹簧模型对盾构隧道接头进行分析,并与有限元结果进行对比;郭瑞等[13]用改进的梁-弹簧模型计算大断面盾构隧道管片的内力,并考虑了接头抗弯刚度与力矩之间的非线性关系;葛世平等[14]运用简化的数值模拟方法,对不同荷载作用下管片接头的变形情况进行了数值模拟和对比分析;庄晓莹等[15]分别采用弹塑性本构和弹塑性损伤本构,建立盾构管片接头的三维有限元模型,模拟了正负弯矩作用下接头的压弯破坏过程;李宇杰等[16]用弹塑性损伤本构建立了三维非连续接触计算模型。本文在平面基本假定的基础上对接头的承载力进行计算,推导出各个阶段的极限弯矩计算公式。该方法不同于已有对管片进行分析的方法,重点考虑了轴力对接头极限承载力的影响,将管片简化成梁模型,通过实例分析对结构在不同轴力作用下进行弯矩校核,计算出不同轴力下的极限弯矩,并确定其破坏模式。
1 混凝土和螺栓的力学特性
混凝土管片接头承载轴力和弯矩的共同作用。运用平面应变假设和应力应变关系,通过轴力平衡计算出受压区高度x,进而判断管片的破坏模式和计算极限弯矩。
由混凝土管片接头的性质可得轴力和弯矩共同作用下的应力分布图,如图1所示。由轴力平衡可得
N+σstAs=σcbx。
(1)
式中:N为管片所受轴力;σst为螺栓所受的拉应力;As为螺栓的有效截面积;σc为混凝土等效矩形应力图压应力;b为管片宽度;x为等效矩形应力图受压区高度。

图1 弯矩轴力共同作用下接头的应力分布
Fig. 1 Stress distribution of segment joint under actions of bending moment and axial force
混凝土的本构关系为
(2)
式中:fc为混凝土的抗压强度设计值;σc为混凝土压应力;εcc为混凝土压应变;ε0为对应混凝土应力刚达到fc时的应变;εcu为混凝土的极限压应变。根据GB 50010—2010《混凝土结构设计规范》[17],取ε0=0.002,εcu=0.003 3。
为了简化公式推导,将混凝土峰值强度之前的本构关系简化为线性模型,即
(3)
其中
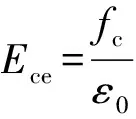
(4)
式中Ece为割线模量或者叫变形模量。对于C50混凝土,Ece=11.5 GPa; 对于C55混凝土,Ece=12.6 GPa。
将螺栓简化为弹性-理想塑性材料,则受拉螺栓的应力σst与螺栓应变的关系表示为
(5)式中:εst为受拉螺栓应变;Es为钢筋的弹性模量;fy为受拉螺栓屈服强度设计值;εy为螺栓的屈服应变;εu为螺栓的极限拉应变,根据混凝土结构设计规范,εu=0.01。
根据GB 50010—2010《混凝土结构设计规范》[17]可知,在弯矩和轴力共同作用下,理想设计的混凝土接头受压区上边缘的压应力和压应变分别达到抗压强度设计值和极限应变,即满足
(6)
式中: α1为常数,其值与混凝土的强度等级有关,对于C50及C50以下的混凝土,α1=1.0;对于C55的混凝土,α1=0.99。
受拉钢筋的应力应变满足
(7)
2 混凝土管片接头破坏模式推导
在轴力和弯矩共同作用下,混凝土管片接头将产生弯曲变形,变形后管片接头的应变分布如图2所示。其中,受压区混凝土的应变近似为三角形分布;而受拉区的应变,对于混凝土为虚拟状态,对于螺栓为真实状态。根据梁平截面变形假定和应变三角形相似关系可知,螺栓拉应变和混凝土压应变的关系为

(8)
式中: h为管片厚度; h0为混凝土截面的有效高度, h0=h-as; as为螺栓中心至混凝土截面受拉边缘的竖向距离; xc为中和轴高度,即受压区的理论高度, xc=x/β1,对于C50及C50以下的混凝土,有β1=0.8,对于C55的混凝土,β1=0.79。

图2 管片接头应变分布简图
由于混凝土和螺栓的本构方程均简化为弹性-理想塑性,而非完全的线弹性,因此,在判断破坏之前,需判断混凝土和螺栓哪个先达到比例极限强度。
2.1 假设螺栓先达到屈服强度设计值
由于螺栓达到屈服强度设计值,有σst=fy,εst=εy。式(8)表示为

(9)
将式(9)代入式(3)得混凝土的应力

(10)
将式(10)代入式(1)中,得
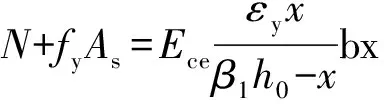
(11)
由式(11)可求出受压区高度x,进而求出受压区理论高度xc,再由式(9)和式(10)求出混凝土压应力σc和压应变εcc。由式(12)判断混凝土的应力状态
(12)
若式(12)成立,表明螺栓先达到屈服强度设计值;若不成立则表示混凝土先达到抗压强度设计值,此时需按混凝土先达到抗压强度设计值的计算方法计算极限弯矩。
2.2 假设混凝土先达到抗压强度设计值
由于混凝土达到抗压强度设计值,有σc=α1fc,εcc=ε0。式(8)表示为

(13)
将式(13)代入式(5)得混凝土的应力
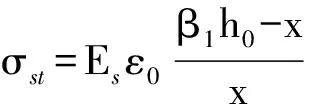
(14)
将式(14)代入式(1)中,得

(15)
由式(15)可求出受压区高度x,进而求出受压区理论高度xc,再由式(13)和式(14)求出螺栓拉应力σst和拉应变εst。由式(16)判断混凝土的应力状态
(16)
若式(16)成立,表明混凝土先达到抗压强度设计值; 若不成立则表示螺栓先达到屈服强度设计值,此时需按螺栓先达到屈服强度设计值的计算方法计算极限弯矩。
2.3 混凝土管片接头极限弯矩计算推导
计算混凝土管片接头的极限弯矩还需判断混凝土和螺栓哪个先达到极限状态。令混凝土压应变εcc为极限状态,即εcc=εcu,由图2和式(8)计算出对应的螺栓拉应变εst,若εst满足式(7),表明混凝土先达到极限状态,即混凝土先被压碎;否则表明螺栓先达到极限状态,即螺栓先被拉断。同理,令εst=εy,由图2和式(8)计算出混凝土压应变εcc,亦可判断出破坏模式。根据破坏模式和图1,由弯矩平衡条件可求得混凝土管片接头极限弯矩Mu。
1)若混凝土先被压碎,同时螺栓处于弹性状态,对受拉螺栓所在位置取矩,得
Mu=α1fcbx(h0-x/2)-N(h/2-as)。
(17)
或受压区混凝土中心取矩有
Mu=EsεstAs(h0-x/2)+N(h/2-x/2)。
(18)
2)若螺栓先被拉断,同时混凝土处于弹性状态,对混凝土中心取矩,得
Mu=fyAs(h0-x/2)+N(h/2-x/2)。
(19)
或受拉螺栓所在位置取矩有
Mu=Eceεcbx(h0-x/2)-N(h/2-as)。
(20)
3)若破坏时螺栓和混凝土均达到塑性状态,上面按弹性计算出的受压区高度不再适用,需按式(21)重新进行受压区高度计算
N+fyAs=α1fcbx。
(21)
此时极限弯矩计算公式为式(17)或(19)。
2.4 混凝土管片接头极限负弯矩计算方法
当计算管片负向极限弯矩时,只需将上面各式中as换为h-as代入计算即可,其中,as为螺栓中心至混凝土截面受拉边缘的竖向距离, h为管片厚度。
3 算例分析
3.1 混凝土管片的轴力分布
图3为混凝土管片接头的轴力分布图。由图3可知,在管片的不同位置轴力不同,因此需要对不同轴力下的极限弯矩进行计算。

图3 混凝土管片轴力分布(单位: kN)
3.2 北京地铁隧道管片接头极限弯矩计算
算例1为北京地铁隧道[18],采用混凝土C50,混
凝土的抗压强度设计值fc=23.1 MPa,管片宽度1.2 m,管片截面高度300 mm,螺栓2个,螺栓中心距管片内缘距离as=120 mm,螺栓等级为A级M24,其性能等级为8.8,屈服强度设计值fy=640 MPa,单个螺栓有效直径21.19 mm,单个螺栓的有效截面积352.5 mm2,As=705 mm2。表1给出了北京地铁隧道管片接头极限弯矩随轴力的变化。
由表1可知,在轴力从200~1 000 kN的变化过程中,管片接头的破坏模式没有改变,均为螺栓先屈服,而混凝土先被压碎。随着轴力的增加,受压区高度增加,管片接头的极限弯矩增加,同时螺栓应变减小。当轴力从200 kN增加到1 000 kN时,极限弯矩增加了86.5%。
3.3 上海地铁隧道管片接头极限弯矩计算
算例2为上海地铁隧道[15],采用混凝土C55,混凝土的抗压强度设计值fc=25.3 MPa,管片宽度1.2 m,管片截面高度350 mm,螺栓2个,螺栓中心距管片内缘距离as=120 mm,螺栓等级为A级M30,其性能等级为5.8,屈服强度设计值fy=400 MPa,单个螺栓有效直径21.19 mm,单个螺栓的有效截面积561 mm2,As=1 122 mm2。表2给出了上海地铁隧道管片接头极限弯矩随轴力的变化。由表2可知,对于该工程从200~1 000 kN的变化过程中极限弯矩增加了85.6%。当轴力为200 kN时螺栓先屈服并先达到极限强度; 当轴力为400~1 000 kN时,管片接头的破坏模式同算例1,即螺栓先屈服而混凝土先被压碎。
3.4 混凝土管片接头极限弯矩有限元分析
以北京地铁为例进行ANSYS分析,验证解析模型的准确性。图4为混凝土管片接头的有限元模型。混凝土采用SOLID65实体单元,螺栓和混凝土中的钢筋采用LINK180三维杆单元,垫块和螺栓帽采用SOLID95实体单元,通过在上端垫块施加位移模拟弯矩作用,混凝土中的钢筋按文献[18]进行配筋。
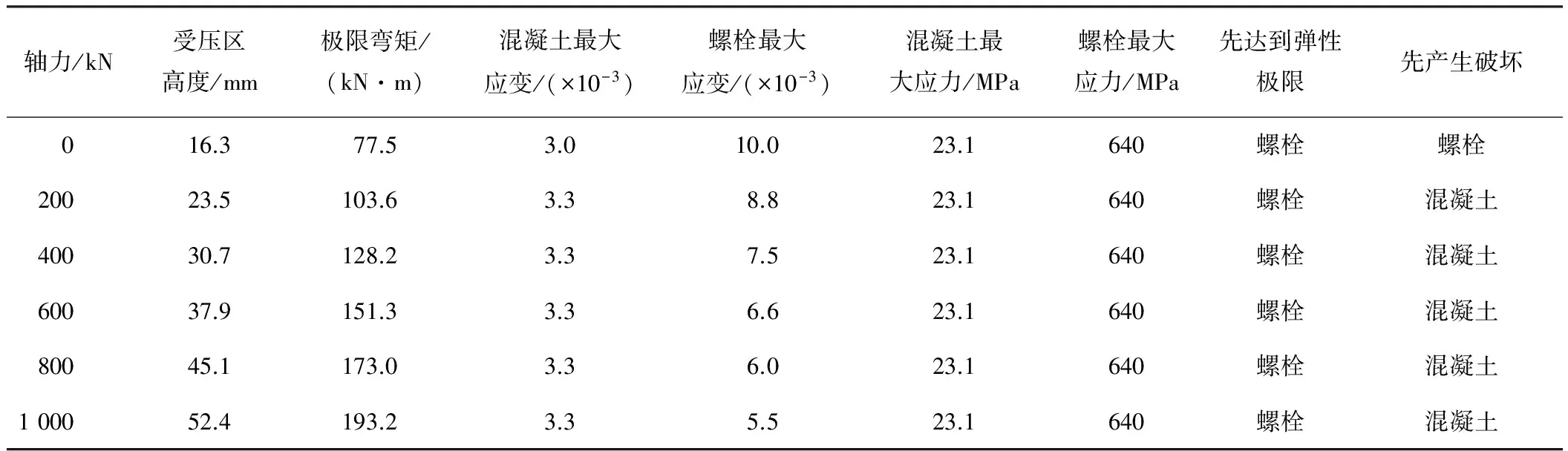
表1 北京地铁隧道管片接头极限弯矩随轴力的变化
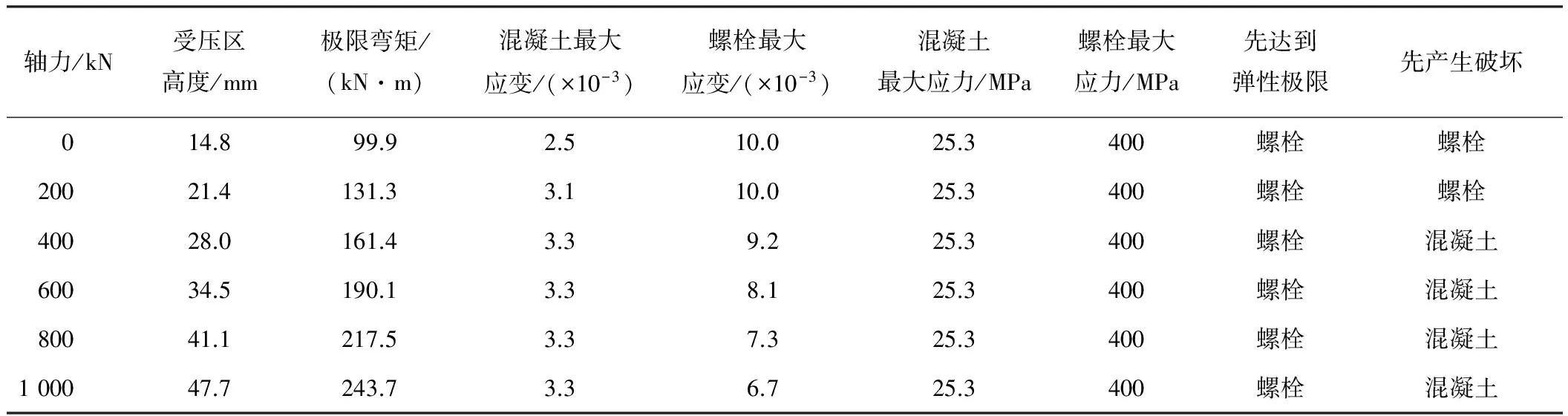
表2 上海地铁隧道管片接头极限弯矩随轴力的变化

图4 管片接头有限元模型
图5为北京地铁隧道管片在轴力为600 kN时管片的应变分布图。此时接头上端混凝土已破坏,压应变为0.003 377,明显较混凝土其他部位的应变大,此时螺栓的拉应变为0.002 6。

图5 混凝土管片压应变分布
图6为混凝土管片的极限弯矩随轴力的变化关系曲线,图6中包含了北京地铁、上海地铁的解析解以及北京地铁的ANSYS分析解。由图6可以看出,混凝土管片极限弯矩随轴力的增加而增加。
比较北京地铁盾构管片极限弯矩的解析解和ANSYS解,可知解析解与ANSYS数值解基本一致,证明了解析计算模型的准确性。

图6 混凝土管片极限弯矩随轴力的变化
Fig. 6 Relationship between ultimate bending moment of concrete segment and axial force
4 结论与讨论
1)针对混凝土管片接头的受力特性,运用弹塑性模型和平截面变形假定,建立混凝土管片接头极限承载弯矩的计算模型,分析管片接头的破坏方式。
2)通过2个算例可知,随着轴力的增加管片接头的极限弯矩承载能力增加。轴力从200 kN到1 000 kN的过程中接头的极限弯矩分别增加了86.5%(北京地铁隧道)和85.6%(上海地铁隧道),最不利荷载组合为最小轴力和最大弯矩组合。
3)通过计算管片接头在不同轴力作用下的极限弯矩,得到的解析解与ANSYS数值解基本一致。验证了将盾构隧道混凝土管片接头简化成梁模型的准确性。
4)在轴力较小的情况下,解析解与ANSYS数值解完全吻合,而随着轴力增大解析解与ANSYS数值解偏差将有少量增加。
5)解析模型中螺栓应变与ANSYS解相比偏大,主要原因为混凝土结构解析模型一般不考虑混凝土的受拉,致使混凝土承担的拉应变全部由受拉螺栓承担。
[1] Mashimo H, Ishimura T. Evaluation of the load on shield tunnel lining in gravel[J]. Tunnelling & Underground Space Technology, 2003, 18(2): 233-241.
[2] CAO Y, WANG P, JIN X, et al. Tunnel structure analysis using the multi-scale modeling method[J]. Tunneling & Underground Space Technology, 2012, 28(1): 124-134.
[3] ZHANG W, Koizumi A. Behavior of composite segment for shield tunnel[J]. Tunnelling & Underground Space Technology, 2010, 25(4): 325-332.
[4] Moller S C, Vermeer P A. On numerical simulation of tunnel installation[J]. Tunnelling & Underground Space Technology, 2008, 23(4): 461- 475.
[5] Do N A, Dias D, Oreste P, et al. 2D numerical investigation of segmental tunnel lining behavior[J]. Tunnelling & Underground Space Technology, 2013, 37(6): 115-127.
[6] CHEN J S, MO H H. Numerical study on crack problems in segments of shield tunnel using finite element method[J]. Tunnelling & Underground Space Technology, 2009, 24(1): 91-102.
[7] 张厚美, 傅德明, 过迟. 盾构隧道管片接头荷载试验研究[J]. 现代隧道技术, 2002, 39 (6): 28-33,41. (ZHANG Houmei, FU Deming, GUO Chi. Study of load test of segment joint in shield driven tunnel[J]. Modern Tunnelling Technology, 2002, 39(6): 28-33,41. (in Chinese))
[8] 张厚美, 过迟, 付德明. 圆形隧道装配式衬砌接头刚度模型研究[J]. 岩土工程学报, 2000, 22 (3): 309-313. (ZHANG Houmei, GUO Chi, FU Deming. A study of the stiffness model of circular tunnel prefabricated lining[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(3): 309-313. (in Chinese))
[9] 黄钟晖. 盾构法隧道管片衬砌纵缝接头受力模型的研究[J]. 地下空间, 2003, 23(3): 296-301,305. (HUANG Zhonghui. Study of loading model of joints at longitudinal seam of lining segments in shield tunnel[J]. Underground Space, 2003, 23(3): 296-301,305. (in Chinese))
[10] 董新平. 盾构管片接头接触面缺陷模型分析[J]. 岩土工程学报, 2013, 35 (7): 1369-1374. (DONG Xinping. Contact surface flaw model for segment joints of segmented tunnel lining[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1369-1374. (in Chinese))
[11] 董新平, 解枫赞. 一类盾构管片接头破坏历程的解析解[J]. 岩土工程学报, 2013, 35 (10): 1870-1875. (DONG Xinping, XIE Fengzan. Analytical solution of segment joint model for segmented tunnel lining[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1870-1875. (in Chinese))
[12] SONG K I, CHO G C, CHANG S B, et al. Beam-spring structural analysis for the design of a tunnel pre-reinforced support system[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59(5): 139-150.
[13] 郭瑞, 何川, 封坤, 等. 大断面水下盾构隧道管片接头抗弯刚度及其对管片内力影响研究[J]. 中国铁道科学, 2013, 34(5): 46-53. (GUO Rui, HE Chuan, FENG Kun, et al. Bending stiffness of segment joint and its effects on segment internal force for underwater shield tunnel with large cross-section[J]. China Railway Science, 2013, 34(5): 46-53. (in Chinese))
[14] 葛世平, 谢东武, 丁文其,等. 盾构管片接头简化数值模拟方法[J]. 岩土工程学报, 2013,35(9): 1600-1605. (GE Shiping, XIE Dongwu, DING Wenqi, et al. Simplified numerical simulation method for segment joints of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(9): 1600-1605. (in Chinese))
[15] 庄晓莹, 张雪健, 朱合华. 盾构管片接头破坏的弹塑性-损伤三维有限元模型研究[J].岩土工程学报, 2015, 37(10): 1826-1834. (ZHUANG Xiaoying, ZHANG Xuejian, ZHU Hehua. 3-D finite element model for destruction process of segment joints of shield tunnel using elastoplastic and damage constitutive methods[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1826-1834. (in Chinese))
[16] 李宇杰, 何平, 秦东平. 基于混凝土弹塑性损伤本构模型的盾构管片受力分析[J]. 中国铁道科学, 2012, 33(1): 47-53. (LI Yujie, HE Ping, QIN Dongping. Force analysis of segment for shield tunnel based on elastoplastic damage constitutive model of concrete[J]. China Railway Science, 2012, 33(1): 47-53. (in Chinese))
[17] 混凝土结构设计规范: GB 50010—2010[S].北京: 中国建筑工业出版社,2010.(Code for design of concrete structures: GB 50010—2010[S].Beijing: China Architecture & Building Press,2010.(in Chinese))
[18] 郭玉海, 陈丹, 袁大军. 北京地铁盾构隧道管片设计合理性探讨[J]. 市政技术, 2006, 24(4): 244-247. (GUO Yuhai, CHEN Dan, YUAN Dajun. Discussion on rationality of segment design for shield tunneling of Beijing Metro[J]. Municipal Engineering Technology, 2006, 24(4): 244-247. (in Chinese))
[19] 陈仁东. 北京地铁四号线管片配筋设计与优化[J]. 现代隧道技术, 2006, 43(5): 50-54,59. (CHEN Rendong. Optimum design for the reinforcement of the lining segments in Beijing Metro Line 4[J]. Modern Tunnelling Technology, 2006, 43(5): 50-54,59. (in Chinese))
Simplified Computing Models for Ultimate Flexural Capacity of Reinforced Concrete Segment Joints Strengthened by Straight Bolts
LI Shouju1, LIU Junhao1, SHANGGUAN Zichang2, YU Shen1
(1.StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,Liaoning,China; 2.CollegeofOceanandCivilEngineering,DalianOceanUniversity,Dalian116023,Liaoning,China)
In order to study the influence of axial force of concrete segment of shield tunnel on ultimate bending moment of segment joint, the concrete segment joint strengthened by straight bolts is simplified as a beam model; and then the computing model for ultimate flexural capacity of reinforced concrete segment is proposed. The equations for force equilibrium and moment equilibrium of segment joint cross-section are derived; and the relationship between bolt stress in tensile zone and ultimate strain of concrete and that between height of compression zone and the ultimate strain of concrete are established based on assumption of plane deformation of segment cross-ssection under the action of bending moment. In case studies, the influence of axial force of concrete segment on ultimate bearing capacity of concrete segment and the broken modes of segment joints are studied. The study results show that the ultimate bearing capacity of segment joint increases with axial force of segment increases. The feasibility of the proposed computing model is verified by comparison between the study results and finite element simulation results.
shield tunnel; ultimate bending moment; bolt; concrete segment; ultimate bearing capacity
2016-04-11;
2016-06-30
国家重点基础研究发展计划资助项目(2015CB057804); 工业装备结构分析国家重点实验室开放基金资助项目(S14206)
李守巨(1960—),男,辽宁沈阳人,1986年毕业于中国矿业学院,矿山建筑工程专业,博士,教授,主要从事计算力学及混凝土结构的教学与科研工作。E-mail: lishouju@dlut.edu.cn。
10.3973/j.issn.1672-741X.2017.01.003
U 45
A
1672-741X(2017)01-0018-06

