浅水极限波浪几何特征的实验研究

陈洪洲，马玉祥，马小舟，董国海

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

浅水极限波浪几何特征的实验研究

陈洪洲1，马玉祥1，马小舟1，董国海1

(1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

该文通过物理模型实验，对浅水区域内的波浪在破碎前极限状态下的几何特征进行了研究。实验基于JONSWAP谱对不规则波浪进行模拟，通过对波群中出现的单体极限波浪进行捕捉并对波形进行测量而得到研究样本。为了考察底坡因素对极限波浪几何特征的影响，实验共考虑了3组大小分别为β=1/15、1/30以及1/45的地形坡度。统计结果表明，在实验所采用的坡度范围内，当地波高与水深对近岸极限波浪的影响最为显著，随着水深与波高因素变化，极限波浪的几何特征也出现明显的改变。坡度因素对极限波陡和偏度的影响很小，可以被忽略，但是对不对称度参数的影响相对比较明显，坡度越陡，不对称程度越剧烈。最后，通过参数化，本文给出了极限波浪几何特征变化的经验公式。

浅水波浪；极限波陡；偏度；不对称度；参数拟合；实验研究；地形坡度

1 引言

波浪在近岸区域传播过程中，随着水深变浅，非线性增强，其前倾的幅度逐渐增大，最终会导致波浪以卷破形式发生破碎。许多学者都曾指出，波浪在传向近岸过程中，会反复拍击停泊在港口的船舶和建筑物，对其造成疲劳破坏，从而影响其使用寿命，并且这一作用会随着波浪在临近破碎前的波形不对称程度的加剧而增强[1—2]。不仅如此，对于研究波浪破碎现象的学者而言，通过对波浪极限状态的研究可以进一步了解整个破碎过程，最终达到可以预测波浪破碎的目的。因此，极限波浪的研究不仅具有重要的工程意义，同时还与理论研究密切相关。目前判断波浪破碎的标准主要通过运动学理论和几何特征两个方面来进行的。基于运动学理论的评判标准指出当波峰粒子的水平速度U超过了波浪本身的相速度C时，破碎就会发生[3—4]。然而，Tian等[5]指出由于无法准确定义不规则波浪的相速度，同时波浪的不规则性导致难以测量波峰水粒子速度，因此该方法无法用于不规则波浪的破碎评判，目前很多学者提出使用波浪破碎前的极限波陡以及相关的极限波浪几何尺度作为特征参量来描述破碎的发生[2,5—6]。

早期Longuet-Higgins[7]通过对真实海面上采集到的波浪数据进行统计，提出当波高(H)为波长(L)的0.12～0.14倍的时候，破碎就会发生。Kjeldsen和Myrhaug[2]通过对挪威沿海采集到的波浪的几何特征进行分析，指出波浪破碎前的波陡(式3)范围约在0.32～0.78之间。尽管波陡参数对于波浪的波形特征而言十分重要，但是由于波陡只是简单的通过波高与波长间的比值来描述波形，并不能完整的反应波浪的不对称性质。因此，Kjeldsen和Myrhaug[2]引入了偏度(式(1))和不对称度(式(2))来更加细致的描述极限波浪的几何特征，并通过对现场波浪进行测量提出，这两个参数的极值分别可以达到2.0和0.9。Bonmarin[8]通过波浪跟踪摄像技术得到的结论显示极限波浪的偏度值变化范围在0.69～0.77之间，而不对称度变化范围则在1.2～2.14之间。由于上述结论大多通过对真实海面进行观测获得，而自然条件下的波浪由于受到多种环境因素影响，破碎过程非常复杂，因此极限波浪的波形参数在一个很宽的范围内。

以往对极限波浪几何特征的研究多集中在深水和有限水深条件下[5,7—8]，而对浅水极限波浪的研究则主要采用现场观测的方法，结果容易受到自然环境影响[2]，此外，这些结论大都是给出一个波形参数在破碎前的临界值，或者一个变化的区间范围作为评判极限状态的参考值，并没有给出这些参量究竟会受到何种因素的影响，以及具体是如何变化的。众所周知，浅水波浪破碎过程非常复杂，不仅对近岸地形的变化起到至关重要的作用，还威胁到近岸建筑物的安全稳定以及使用寿命[2]。因此，通过精确的物理实验对近岸浅水下的极限波浪进行研究统计具有重要的科学和工程意义。

2 关于极限波浪几何参量的定义

对波浪在极限状态下的几何特征进行准确的定量描述，有助于更深入的了解波浪在破碎前的形态[2,6]，而波浪的几何特征通常通过波陡参数和不对称参数进行描述，通过对所测波列中的单体极限波浪进行采集分析可以得到这些波形特征参数(图1所示)。平均波陡(εm)由于同时考虑了波浪前部和后部的变化因素，能够比较全面的描述波浪几何特征，因此被该文采用来进行极限波浪的波陡参数统计，根据Kjeldsen和Myrhaug[2]以及Babanin等[6]提出的，波浪关于水平不对称度(偏度参数Sk)和垂向不对称度(不对称度参数As)可以定义为：

(1)

(2)

而平均波陡可以定义为：

(3)

式中，ηc为波峰，ηf为前向波谷，ηr为后向波谷；Lm为平均波长，由如下色散关系计算得到：

(4)

式中，T代表波浪中间部分传播的时间长度，d是当地水深。

3 实验介绍

3.1 实验设备

本实验是在大连理工大学海岸与近海工程国家重点实验室的海洋环境水槽中进行的。水槽总长(Lt)为50 m，总宽(Wt)3 m，最大深度(Dt)为1 m，实验水深为0.52 m。详细的实验布置如图2所示，为减小底坡反射，每组模型坡脚处均设置速升段，通过改变速升段高度对坡度β大小进行控制，本实验共考虑了3组底坡大小分别为1/15、1/30以及1/45的地形进行实验。水槽一端配备有液压驱动的不规则造波机，x轴的原点固定在造波板伸缩的平均位置，波浪传播方向为正，水槽末端安置有消浪网用来减弱波浪反射的影响。为确保实验波浪的二维性，从x/Lt=0.26处起，用一块光滑的有机玻璃板将水槽沿纵向方向分隔为两段，其中较狭窄的宽度为1.2 m的槽段被用来作为数据采集区域。

实验中所用到的浪高仪为标准电阻式波高测量仪，沿水槽方向布置了10个不同的测点。1号浪高仪放置在x/Lt= 0.26处，用来测量初始波要素；2号和3号浪高仪分别置于x/Lt=0.386和0.45处，用来测量浅水变形；5号、6号和7号浪高仪放置在破碎带内(x/Lt= 0.49，0.51，0.53)，用来测量破碎区内的波况；8号、9号和10号浪高仪依次放置在堤顶处(x/Lt= 0.56，0.59，0.62)，用来测量波浪破碎后在堤顶的演化情况。实验中，根据破碎发生位置，移动4号浪高仪，使之恰好位于破碎点前端，从而可以捕捉极限波浪的波形。

图2 实验布置图Fig.2 Expeimental set-upa.断面示意图，b.平面示意图a.Cross-section view, b.plane view

3.2 波况参数

本研究对不规则波浪进行模拟，采用的是改进后的平均JONSWAP型海浪谱，具体表达式如下：

(5)

式中，S(f)为谱密度函数，f为波浪成分的自带频率，Tp为谱峰频率，γ是谱峰升高因子(本实验γ=3.3)，谱型参数σ控制频谱的偏度特征，当f<1/Tp时，σ=0.07，否则σ=0.09。βJ定义为谱宽参数，可以控制频带的相对宽度，详细波浪参数如表1所示，其中Tp为谱峰周期，Hrms0表示对应的深水均方根波高，是基于对1号浪高仪采集到的波浪数据通过线性变浅公式(6)换算而得到(式中H和L代表变浅过程中位于水深d处的特征波高和特征波长。H0是与H对应的深水波高)，每一组波浪序列采集时间间隔为0.02 s，采集时长共163.84 s。为得到充足数据进行统计并保证实验的可重复性，每组实验重复进行3次采集。

(6)

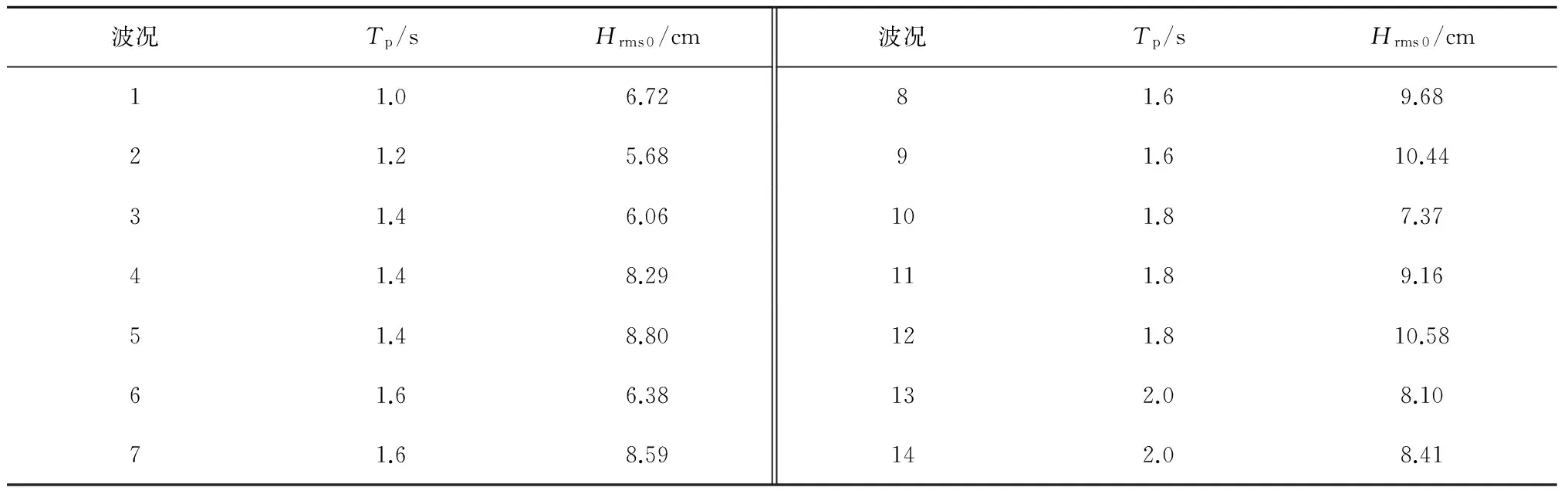
表1 实验波浪参数

3.3 测量步骤

众所周知，波浪在破碎过程中的变形转瞬即逝，由于本实验采用不规则波况作为入射波进行试验，因此在变浅过程中，破碎发生多会集中在某一特定区域内，这一区域通常被称为破碎带，为了尽可能多的采集到波浪在破碎前的波形变化情况，在实验中，根据目测观察到的破碎带区域位置来调整4号浪高仪位置，使之恰好位于初始破碎点。这样一来，当破碎带内发生波浪破碎时，4号浪高仪刚好可以采集到对应波浪在破碎前的极限波形。采集结果如图3所示，图3a和3b分别为4号和5号浪高仪采集到的波面序列，可以看到在150 s左右有个波浪达到了极限状态，随后发生破碎而导致波高迅速衰减。关于这个极限波浪衰减前后的详细情况可以通过图3a1和3b1给出的局部放大图清晰的看出，因此4号浪高仪采集到的位于150 s处的波浪被提取出来作为一个单体极限波进行分析。本研究所采用的极限波浪均是通过上述方法进行分析得到。需要指出的是，除了4号浪高仪临近位置处破碎发生较频繁外，坡上其余浪高仪临近位置处均有破碎发生，对这一部分极限波浪数据也一并进行统计。

需要指出，本研究对极限波浪的选取是基于浪高仪采集到的以时间为变量的波面序列，并不能真实的反映实际波面状况，样本选取也具有一定的主观性，因此，测量结果在某种程度上只代表了波形特征的平均水平。要想真实地还原波浪在破碎前的极限状态，就必须使用高速摄像机对整个破碎过程进行拍摄，寻找最接近破碎临界点的波浪进行统计，才能得到最真实的极限波浪波形特征。

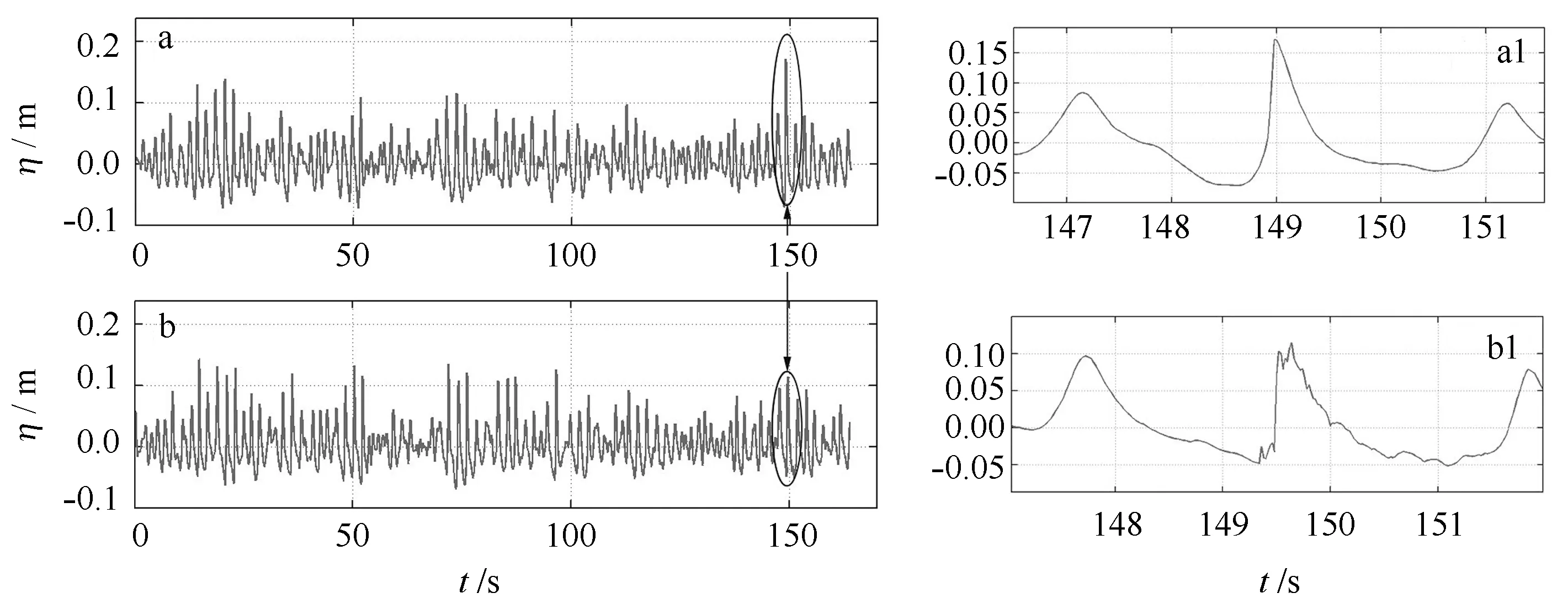
图3 两个相邻测点处的波面示意图Fig.3 The surface elevation at two adjacent stations

4 结果讨论

4.1 关于平均波陡的讨论

Kashima等[9]指出，浅水条件下的极限波浪非线性特征由于受到变浅效应以及地形的影响会表现的比深水情况更为剧烈。大量研究都指出波浪在浅水中的波高分布与当地波高与水深的比值(H/d)密切相关[10—11]。因此，本文围绕极限波浪特征与当地Hs/d的关系变化展开研究，其中Hs为测点处波列的有效波高。此外，众所周知，极限波浪的产生与非线性相互作用紧密相关，而波浪在近岸传播过程中，岸底坡度会显著影响波浪的非线性相互作用程度[9,12]，从而进一步对极限波浪的几何特征产生影响，因此，波浪在传播时的波形变化除了受到水深以及波高的影响外，另一个重要的影响因素便是地形坡度[9,12]。为了考察地形坡度对极限波浪波形特征的影响程度，这里将3组不同底坡上测得的数据放在一起进行比较。

图4给出的是3个坡度下极限波浪的平均波陡(εm)与Hs/d之间的关系，通过观察可以发现，随着水深减小，受变浅效应和非线性相互作用的影响[9,12]，εm呈现总体增大的变化趋势。当波浪位于水深区间为Hs/d≤0.45时，εm值基本保持恒定不变，在0.4上下浮动，然而当位于Hs/d>0.45区间内时，εm开始有明显的增大趋势，从0.4缓慢增至0.6左右，这意味着当水深在一定范围内变化时，极限波浪中心波陡可以维持在一个相对稳定的水平上。值得一提的是，Toffoli等[13]在深水实验条件下得到的εm值范围在0.40～0.44之间，另外，Ramberg和Griffin[14]在中等水深条件下得出的εm值为0.41，这些结论都与本文得到的初始值基本接近。

通过将不同底坡上得到的结论进行比较可以看到，不同坡度下的εm值变化趋势基本一致，这里用最小二乘法对3组坡度下的εm值与对应的Hs/d参数间的关系进行拟合，结果见公式(7)和(8)。表2给出的是公式(8)与3个坡度下的数据之间对应的相关系数R2的结果，R2值均大于0.8，说明公式可以比较好的描述平均波陡εm的变化情况，同时也说明坡度的影响较小，基本可以忽略。

Hs/d≤ 0.45 εm=0.4,

(7)

(8)

图4 不同坡度下测得的极限波浪平均波陡εm与Hs/d间的关系(实线为拟合曲线)Fig.4 Limiting mean steepness with respect to Hs/d on different slopes(the solid line is the fitted result)

Tab.2 Summary of the related coefficients of Eq. (8) forεmon different bottom slopes

坡度1/151/301/45R20.870.830.81

4.2 关于偏度和不对称度的讨论

通过对极限波陡参数的研究，可以对波浪在极限状态下的波高与波长间关系变化有一定了解，然而仅凭波陡参数是不能够全面描述近岸波浪的几何特征的，波浪在近岸传播时受非线性相互作用影响，波形会逐渐前倾，波峰抬高的同时波谷变得扁平，这一系列变化的发生，标志着极限波浪会携带大量的不对称特征信息，而偏度和不对称度是其中最为重要的两组参数。

图5给出的是不同坡度下极限波浪的偏度Sk和与之对应的平均波陡εm间的关系，可以看到，当对应的平均波陡从0.2增大至0.7的过程中，偏度值一直为正，并且也在缓慢的增长，本实验得到的Sk的上限值为1.5，比Babanin等[6,15]以及Toffoli等[13]提出的深水条件下极限波浪的偏度范围0～1要大。对于Stokes二阶波浪而言，Sk理论值为0.61，对应的极限波陡为0.443，明显比实验值小，这是由于考虑波浪非线性程度较弱而造成的。此外，不同坡度下Sk的变化趋势基本相同，说明极限波浪偏度并不受岸底坡度的影响。Kjeldsen等[16]提出深水条件下波浪的Sk值在0上下浮动，因此Sk=0作为描述Sk变化的初始值被考虑进经验公式中去，通过最小二乘法对Sk和εm间的关系进行拟合，得到如下结果:

(9)

图5 不同坡度下测得的Sk与对应εm的关系(实线为拟合曲线)Fig.5 Limiting wave skewness with respect to εm on different bottom slopes (the solid line is the fitted result)

图6所示的是极限波浪的不对称度As与其对应的平均波陡εm间的关系。与Sk变化方向正好相反，As随着εm增大，从正值0.8逐渐减小至-0.9。本实验测得的As上限与Kjeldsen等[16]在深水条件下得到的结论为0.9基本符合。此外，Toffoli等[13]在中等水深条件下得到的As值范围为-0.4～0.8，略窄于本文在浅水条件下得到的范围，这说明波浪在浅水条件下能够达到的极限不对称程度比深水条件下更大。

通过观察As在不同底坡上的变化可以发现，在较陡的1/15坡度上时，As的变化明显更加剧烈。这是由于波浪不对称度与能量传递密切相关引起的，Kashima等[9]指出波浪在较陡底坡上传播时的能量传递比缓坡上更加强烈，因此，1/15坡度上的As变化幅度相对其他两个坡度下表现更加剧烈。这里，将深水情况下测得的As=0.8作为初始值，同样采用最小二乘法对实验数据进行拟合，得到波浪在极限状态下的波形不对称度As的经验公式(10)和(11)，表3给出的是该组公式与3个坡度下的数据之间对应的相关系数R2的结果，R2值均大于0.85，说明公式可以很好地描述Sk在浅水中的变化情况。

(10)

(11)

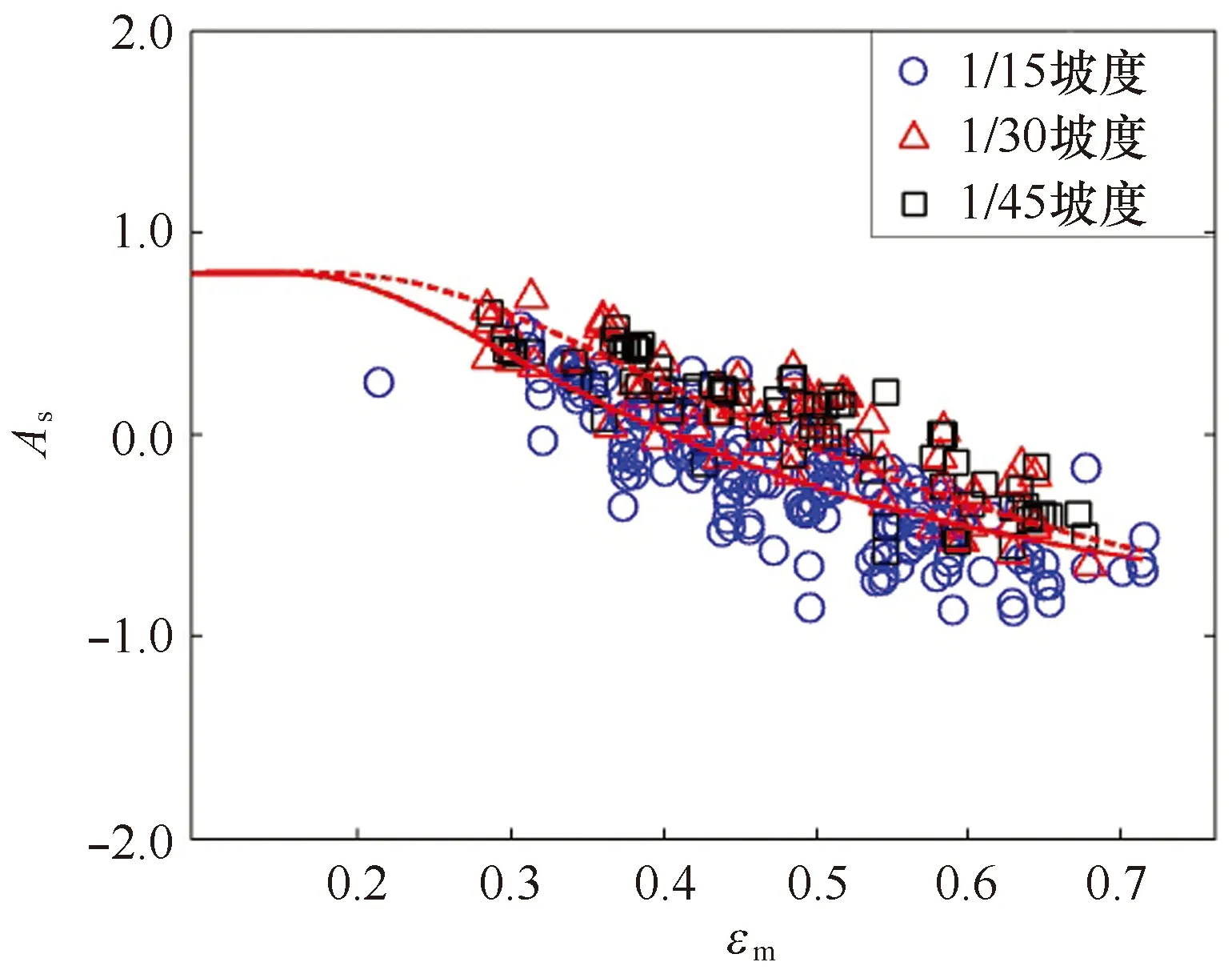
图6 不同坡度下测得的As与对应εm的关系，实线为1/15坡度下的拟合结果，虚线为1/30和1/45坡度下的拟合结果Fig.6 Limiting wave asymmetry with respect to εm on different bottom slopes; the solid line is the fitted result for 1/15 slope bottom and dashed line is for 1/30 and 1/45 slope bottom

坡度1/151/301/45R20.910.880.90

5 结论

本文通过物理模型实验对浅水区域内极限波浪的波陡参数以及不对称特征进行了研究，为了考察地形坡度的影响，本实验分别进行了随机波浪在3个不同地形坡度(β=1/15、1/30、1/45)上的传播实验。通过对波列中出现的极限波浪进行测量分析发现，当地波高与水深对极限波浪的几何特征影响最为显著，随着水深与波高因素变化，极限波浪的几何特征也出现明显的改变。而在本实验所采用的坡度范围内，坡度因素仅对不对称度参数有影响, 坡度越陡，极限波浪表现出的不对称程度就越剧烈。最后，基于实验结果，进而拟合出了平均波陡及偏度和不对称度变化的经验公式。

[1] Peterson P, Soomere T, Engelbrecht J, et al. Soliton interaction as a possible model for extreme waves in shallow water[J]. Nonlinear Processes in Geophysics, 2003, 10(6): 503-510.

[2] Kjeldsen S S, Myrhaug D S. Breaking waves in deep water and resulting wave forces[C]//Proceedings of the 11th Offshore Technology Conference. Houston, Texas, USA: Offshore Technology Conference, 1979: 2515-2522.

[3] Nepf H M, Wu C H, Chan E S. A comparison of two-and three-dimensional wave breaking[J]. Journal of Physical Oceanography, 1998, 28(7): 1496-1510.

[4] Wu C H, Nepf H M. Breaking criteria and energy losses for three-dimensional wave breaking[J]. Journal of Geophysical Research, 2002, 107(C10): 41-1-41-18.

[5] Tian Zhigang, Perlin M, Choi W. Evaluation of a deep-water wave breaking criterion[J]. Physics of Fluids, 2008, 20(6): 066604.

[6] Babanin A, Chalikov D, Young I, et al. Predicting the breaking onset of surface water waves[J]. Geophysical Research Letters, 2007, 34(7): L07605.

[7] Longuet-Higgins M S. On the statistical distribution of the heights of sea waves[J]. Journal of Marine Research, 1952, 11(3): 245-266.

[8] Bonmarin P. Geometric properties of deep-water breaking waves[J]. Journal of Fluid Mechanics, 1989, 209: 405-433.

[9] Kashima H, Hirayama K, Mori N. Shallow water effects on freak wave occurrence[C]//Proceedings of the 22nd International Offshore and Polar Engineering Conference. Rhodes, Greece: IOPE, 2012: 778-783.

[10] Goda Y. Numerical experiments on statistical variability of ocean waves[J]. Report of the Port and Harbour Research Institute, 1977, 16(2): 3-26.

[11] Battjes J A, Groenendijk H W. Wave height distributions on shallow foreshores[J]. Coastal Engineering, 2000, 40(3): 161-182.

[12] Gramstad O, Zeng H, Trulsen K, et al. Freak waves in weakly nonlinear unidirectional wave trains over a sloping bottom in shallow water[J]. Physics of Fluids, 2013, 25(12), 122103.

[13] Toffoli A, Babanin A, Onorato M, et al. Maximum steepness of oceanic waves: field and laboratory experiments[J]. Geophysical Research Letters, 2010, 37(5): L05603.

[14] Ramberg S E, Griffin O M. Laboratory study of steep and breaking deep water waves[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1987, 113(5): 493-506.

[15] Babanin A V, Chalikov D, Young I R, et al. Numerical and laboratory investigation of breaking of steep two-dimensional waves in deep water[J]. Journal of Fluid Mechanics, 2010, 644: 433-463.

[16] Kjeldsen S P, Vinje T P, Myrhaug D P, et al. Kinematics of deep water breaking waves[C]//Proceedings of the 12nd Offshore Technology Conference. Houston, Texas, USA: Offshore Technology Conference, 1980: 3714.

Laboratory study on geometric characteristics of limitting waves in shallow water

Chen Hongzhou1, Ma Yuxiang1, Ma Xiaozhou1, Dong Guohai1

(1.TheStateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116024,China)

Physical experiments were carried out in a wave flume to examine the geometric characteristics of limiting gravity waves propagating in shallow water. Several random wave trains varying height and peak frequency were generated using JONSWAP spectra. Three bottom slopes (1/15, 1/30, 1/45) were installed in the wave flume and the influence of slope bottoms were also considered. Limiting waves were captured from the measured wave trains and the geometric characteristics of its waveform were analyzed. It is found that in the range of bottom slope adopted in this experiment both initial wave heights and local water depth have significant influence on the limiting characteristics of shallow water waves. With the influence of these factors, the geometric of extreme waves are developed. The bottom slopes effect to the limiting steepness and skewness could be neglected, however, it has obvious influence to the limiting wave asymmetry. It will show a more severe asymmetry when waves are on a steeper bottom. Furthermore, the empirical formulae regarding the relationships between geometric characteristics and the local nondimensional wave height were derived.

shallow water waves; extreme wave steepness; skewness; asymmetry; parameterization; laboratory study; bottom slope

10.3969/j.issn.0253-4193.2017.02.010

2016-03-03；

2016-06-10。

国家重点基础研究发展计划(2011CB013701)；国家自然科学基金(51679031)；全国高等学校优秀博士论文作者专项资助(201347)。

陈洪洲(1986—)，男，新疆乌鲁木齐市人，博士生，从事近岸波浪非线性变形的研究。E-mail:379988848@163.com

TV139.2+5

A

0253-4193(2017)02-0105-07

陈洪洲，马玉祥，马小舟，等. 浅水极限波浪几何特征的实验研究[J].海洋学报，2017，39(2)：105—111,

Chen Hongzhou, Ma Yuxiang, Ma Xiaozhou，et al. Laboratory study on geometric characteristics of limitting waves in shallow water[J]. Haiyang Xuebao，2017，39(2)：105—111, doi:10.3969/j.issn.0253-4193.2017.02.010