基于等效传递函数匹配的非侵入电容电流检测电路的设计与应用

杨异迪，卢伟国，周雒维

（重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044）

基于等效传递函数匹配的非侵入电容电流检测电路的设计与应用

杨异迪，卢伟国，周雒维

（重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044）

结合一类简化的非侵入式电容电流检测结构，提出了检测和被测支路二者的等效传递函数近似相匹配的设计思路，给出了参数设计条件并验证了其非侵入检测特性。以Buck变换器的电容电流检测为例，应用所提检测电路构建了电容电流滞环控制电路方案。稳态实验结果表明所提采样电路能够实现电解电容电流的高精度检测，负载的动态实验结果表明所构建滞环控制具有快速负载动态调节能力。

非侵入；电容电流检测；Buck变换器；滞环控制；传递函数

负载瞬态特性在多数开关功率变换器系统中是一个重要的动态性能指标，提升该特性的基本思路是引入负载前馈控制。输出电容电流能及时反映负载的变化信息，以其构建的控制策略可以极大提升变换器的负载瞬态特性。文献［1-2］中所设计的变换器负载动态最优控制电路中，均含有关键的电容电流检测环节；文献［3-4］提出的等效恒频滑模控制电路中也进行了电容电流的采样；此外，基于电容电流反馈的并网逆变器控制策略［5-6］同样需要进行电容电流的采样。

文献［2］基于阻抗匹配思想实现了一种非侵入式电容电流检测方案，并联的检测支路采用了小电容和运放相串联的电路结构，但是文中并未给出检测电路的参数设计细节，也没有讨论被测电容寄生参数对检测的影响。事实上，被测电容支路寄生参数的存在会影响电容电流检测的精确性，特别是在超高频工作场合和电解电容应用场合，此二者对应的电容寄生参数均不可忽略。文献［7-8］提出了一类简化的非侵入电容电流检测方案，其设计思想与文献［2］一致，通过设计检测和被测支路的总等效阻抗相匹配来计算有关检测参数，但是所提的参数设计思路不易理解，所选实验参数与理论公式计算有出入，文中对此也没有进行解释和说明。此外在开关变换器选用的电解电容场合中，其寄生参数同样影响大，因此在非侵入式电流检测电路设计中则必须考虑寄生参数的影响。目前关于电解电容电流非侵入式检测鲜有文献进行讨论和分析［9］。

本文结合文献［7-8］所提简化的非侵入式电容电流检测结构，提出了基于等效传递函数相匹配的参数设计新思路，即设计检测支路与被测电容支路的等效传递函数近似相等，检测支路阻抗远大于被测支路阻抗。给出了电路参数设计条件，结合Buck DC/DC变换器对象，验证所提电解电容电流检测的动稳态结果和非侵入特性，并进一步结合滞环控制的应用，给出有关负载动态的实验验证。

1 非侵入式电容电流检测原理和设计方法

1.1 检测原理

文献［7-8］所提简化的非侵入式电容电流检测电路结构如图1所示，其中vo为输出电压，C为被测输出滤波电容，L为滤波电感等效串联电感ESL，R为等效串联电阻ESR，iC为其电流。

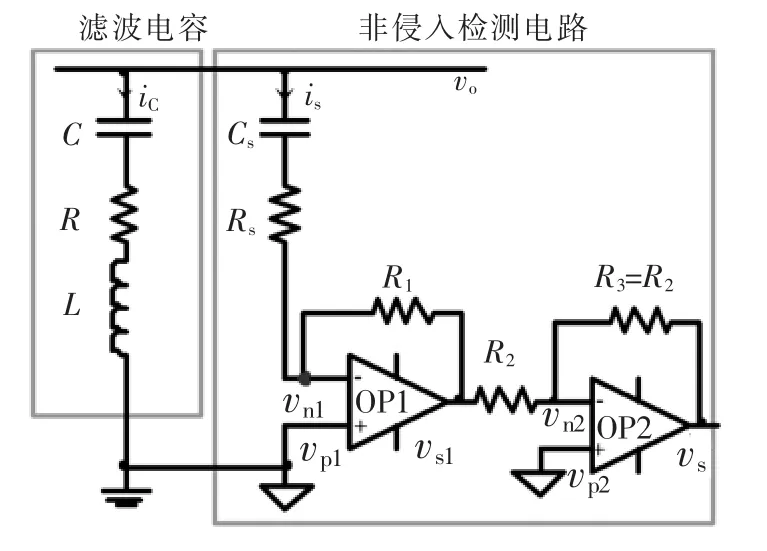
图1 非侵入式电容电流检测电路Fig.1 Non-invasive capacitor-current sensing circuit

非侵入采样电路中OP1、OP2为运算放大器，is为流过采样电路的电流。由于实际运放的带宽和增益有限，如此在信号频率较高时，其开环幅频特性不再是高增益直流环节，而表现出高频动态衰减特性。仅考虑运放的主极点影响，实际运放的开环传递函数可近似为一阶惯性环节Gop（s）≈K/（T1s+1），如图2所示，其中f1为其转折频率，T1=1/f1，K为运放开环直流增益，ΔB为其带宽，ΔB≈K/T1。

则运算放大器OP2的闭环传递函数可表示为

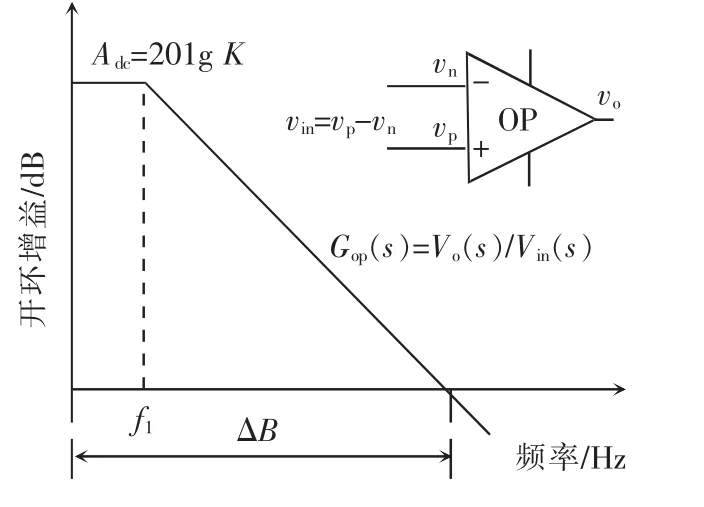
图2 运放开环幅频特性Fig.2 Open-loop amplitude-frequency characteristic of an operational amplifier

当|Go2（jω）|＞＞1时，闭环传递函数Go2（s）≈1。取|Go2（jω）|＞10可得近似条件ΔB/10＞fs，其中，fs为被测电容电流的工作频率。当满足近似条件时，运放OP2环节可简化为-1比例环节。

基于叠加原理，图1中运算放大器OP1反相端节点电压vn1可表示为 vn1=vn1_1+vn1_2， 其中 vn1_1为输出vo单独作用所对应的分量，vn1_2为输出vs单独作用的反馈分量。由此，可以构建出相应系统信号，结构框图如图3所示，图中各大写分量分别为时域量所对应的频域分量。

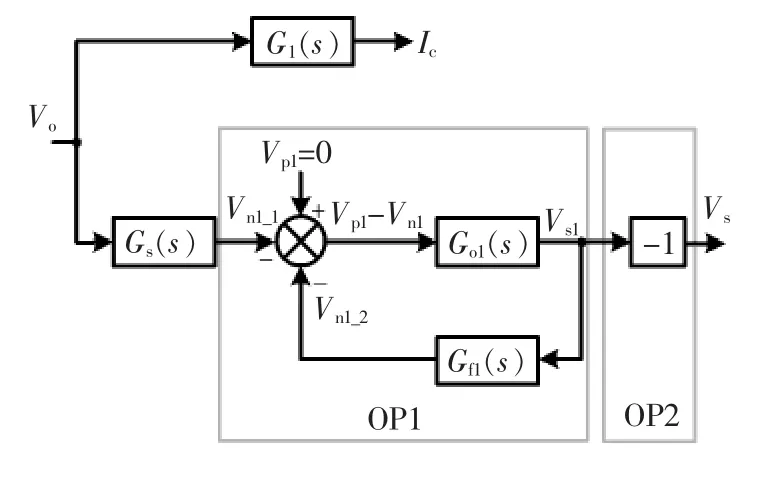
图3 简化后系统结构框图Fig.3 Block diagram of simplified system

图3中有关传递函数分别表示为

采样电路输出信号Vs（s）的传递函数可表示为

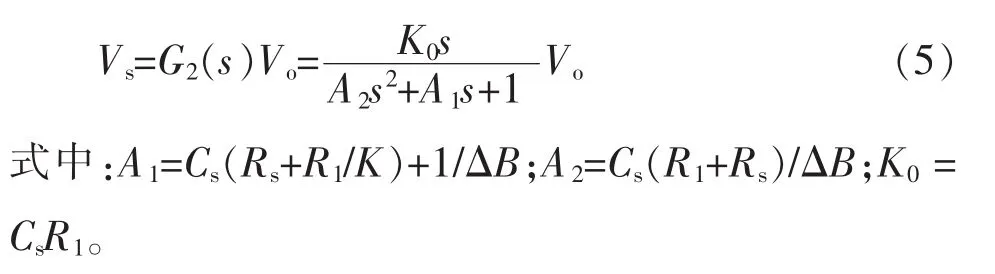
对比式（2）和式（5），当|G1（s）|≈|G2（s）|，即2个传递函数完全匹配时，时域上有vs≈iC，如此实现了电容电流iC的检测。

1.2 参数设计方法

要实现传递函数G1（s）和G2（s）的匹配，分母多项式系数应对应相等。则传递函数匹配条件如下：①A2→CL；②A1→CR。设Cs=C/n，n为比例系数，则有

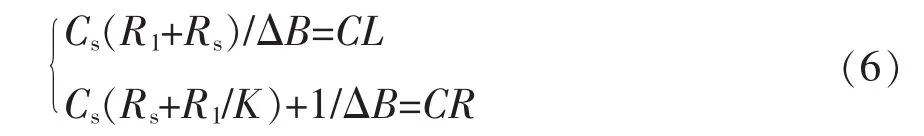
考虑到运算放大器直流增益K非常大，可忽略R1/K项，则检测回路参数设计为

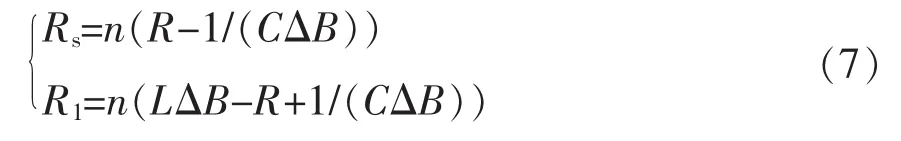
当满足式（7）条件时，|G2（s）|≈（R1/n）|G1（s）|。选择合适的ΔB，可使信号比例系数kc=（R1/n）≈1，即运算放大器输出与检测电容电流幅值相等，此时ΔB为

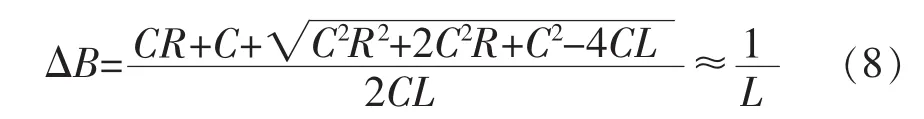
此外，实现非侵入检测，必须保证检测支路的阻抗Zs远大于滤波电容支路阻抗Zc。结合运算放大器小信号模型，图1非侵入检测电路的等效电路如图4所示。其电路关系表示为

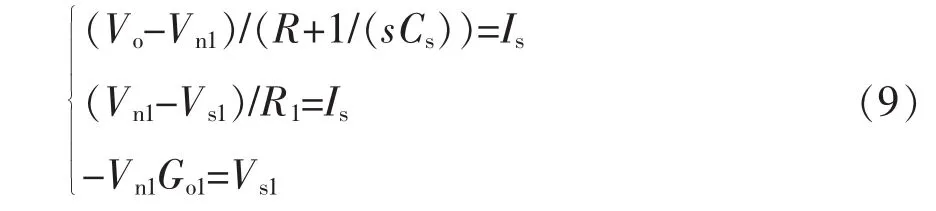
不妨定义被采样电容支路阻抗Zc=R+1/（sC）+ sL。由式（9）可得检测支路阻抗Zs=Vo/Is，结合式（7）可得

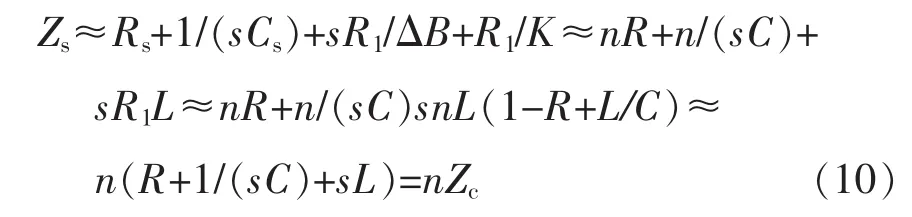
当n取较大数值时，检测电路输入阻抗远大于被测电容支路阻抗，即可实现非侵入检测目的。

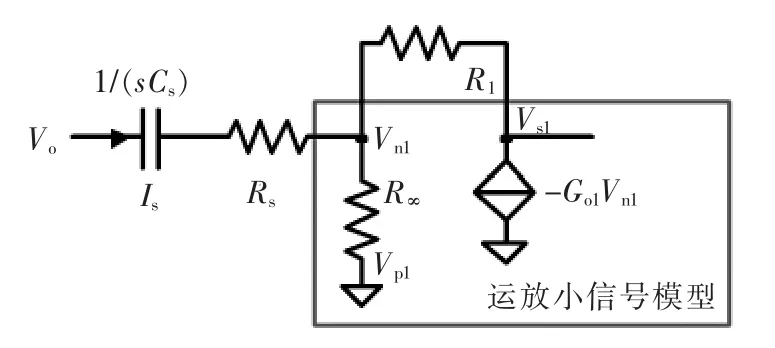
图4 基于运放小信号模型的检测电路Fig.4 Sensing circuit using small signal model of the amplifier

2 理论分析与实验验证

本文选取铝电解电容作为被检测电容，经仪器测得其寄生参数如表1所示。

将表1参数代入式（2）可得

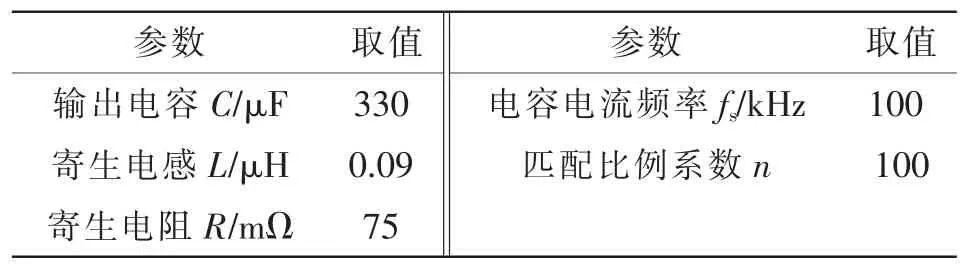
表1 铝电解电容参数和采样信号参数Tab.1 Circuit parameters of an aluminum electrolytic capacitor and sampled signal

根据设计条件式（8），理论上选取ΔB≈1/L≈11.1 MHz可实现放大系数kc约为1，但实际运放参数一般不能恰好匹配。实验中选择运算放大器AD823，从Datasheet中可知，在供电电压为±15 V、带宽ΔB=16 MHz时，kc略大于1，其他近似条件也能满足。最终匹配网络参数选取如表2所示。

将以上参数代入式（5）中，可得

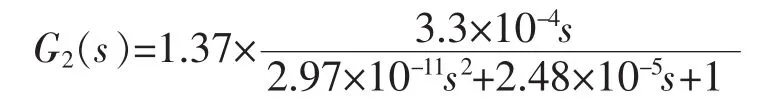
G1（s）和G2（s）分母多项式相等，幅值存在检测放大倍数kc=1.37。

匹配检测电路参数如表2所示。根据表1、表2，可求得滤波电容支路阻抗Zc和检测电路输入阻抗Zs分别为

Zs≈nZc≈100 Zc检测电路阻抗远大于滤波电容支路阻抗，满足非侵入检测要求。

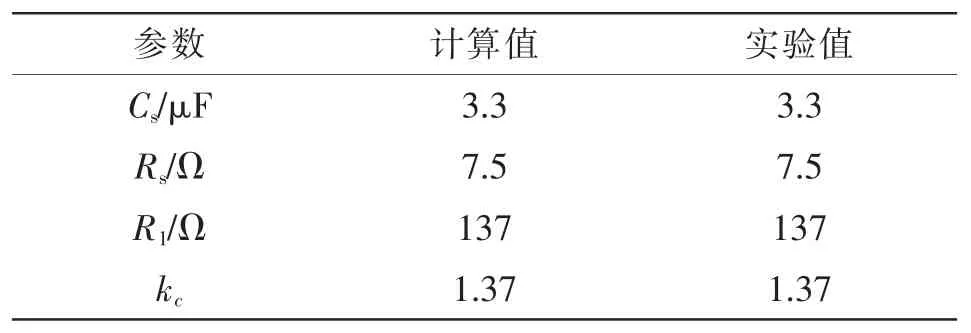
表2 匹配检测电路参数Tab.2 Circuit parameters for the current sensing circuit

以开关频率为100 kHz的Buck变换器电容电流检测为例，实际检测实验波形如图5所示，检测信号与实际信号相位一致，幅值为实际信号1.4倍左右，与理论分析一致。

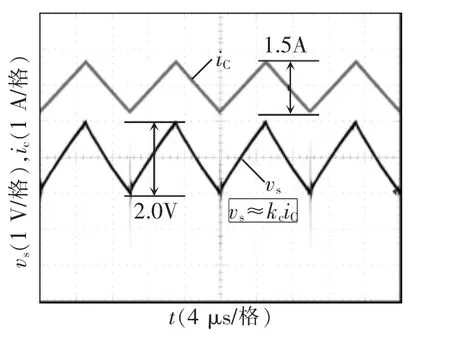
图5 电容电流检测实验结果Fig.5 Experimental results for iCsensor

3 Buck变换器的滞环控制应用

结合所提非侵入式电容电流检测设计方法，构建了电容电流滞环控制并应用于Buck变换器，实验主电路和控制电路如图6所示。其中实验电路参数为：输入电压Vin=30 V，输出参考电压15 V，目标开关频率设计为100～200 kHz，采用表2数据即可满足要求。为了平衡检测电路放大倍数kc= 1.37，设计OP2闭环增益约为1/kc（R2=5.1 kΩ和R3=3.7 kΩ）来实现 vs=iC，OP2型号同样选择为AD823（ΔB/10=1.6 MHz＞＞100 kHz），此时OP2部分可视为比例环节。

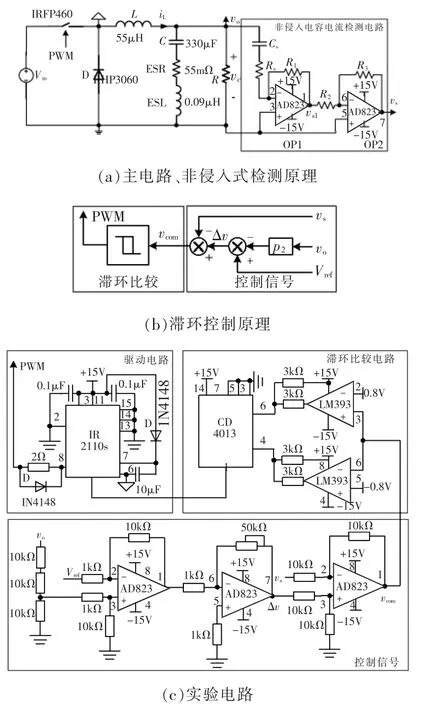
图6 滞环控制Buck变换器Fig.6 Hysteretic controlled Buck converter

图6（a）给出了实验中主电路参数以及非侵入式电容电流检测电路的具体结构，其参数与表2中数据相同；图6（b）和（c）分别为滞环控制的结构框图和实验电路原理。控制信号由电压误差信号Δv和检测电容电流信号vs构成，经过滞环比较器控制Buck变换器工作。其中，滞环比较电路由比较器LM319以及RS触发器CD4013构成，驱动电路采用IR2110S芯片，通过自举电容实现Buck电路浮地驱动。

稳态时检测结果如图7所示。由图可见，非侵入式检测电容电流信号vs与电感电流iL纹波 （电容电流）一致。

负载上跳（1.5 A→7.5 A）和下跳（7.5 A→1.5A）实验波形分别如图8和图9所示。由图可见，在负载跳变时刻，vs能快速反应电容电流突变信息，实现动态过程中开关的全开全关快速调节。

所提非侵入式电容电流检测方案在稳态和动态情况下均能较好地跟踪被测电容电流信号。

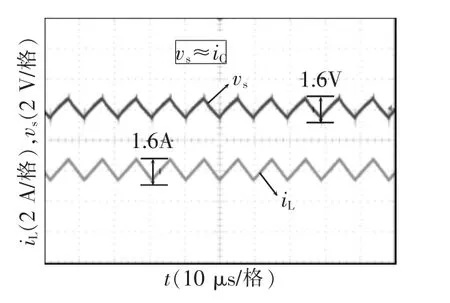
图7 检测电容电流信号vs和电感电流iL的实验波形Fig.7 Experimental results for sensed capacitorcurrent vsand inductor current iL

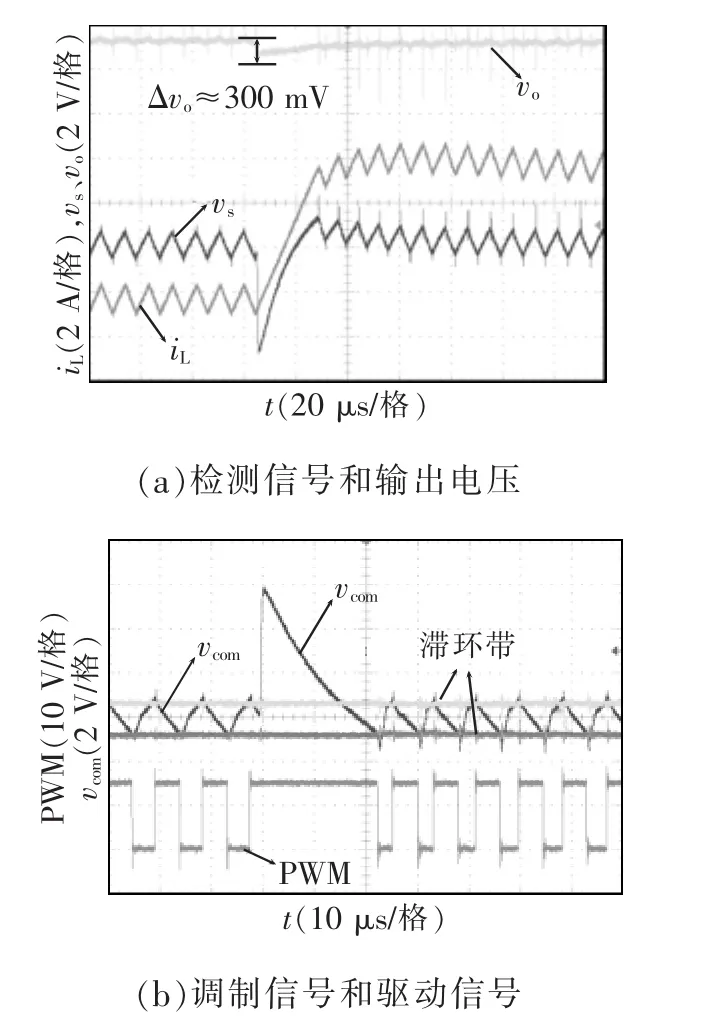
图8 负载上跳（1.5 A→7.5 A）实验波形Fig.8 Experimental waveforms for load step（1.5 A→7.5 A）

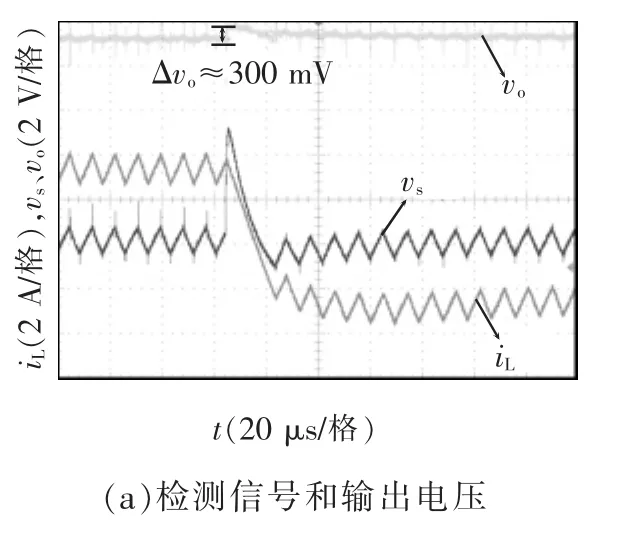
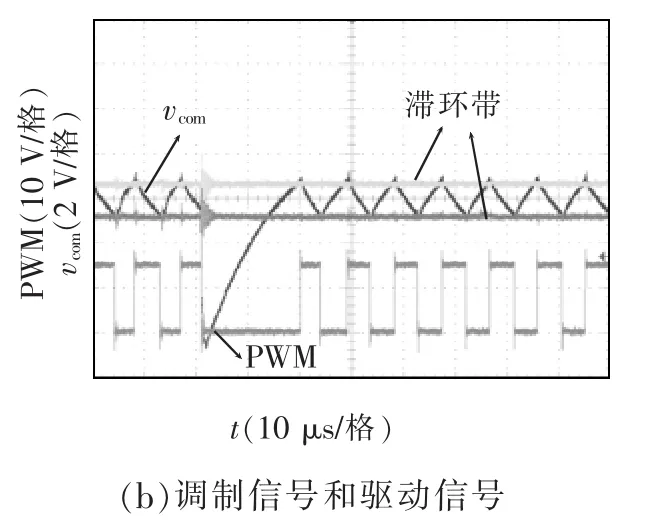
图9 负载下跳（7.5 A→1.5 A）实验波形Fig.9 Experimental waveforms for load step（7.5 A→1.5 A）

4 结语

本文结合一类简化的非侵入电容电流检测结构，提出了基于传递函数匹配的非侵入式电容电流采样电路参数设计方案。针对电解电容进行了非侵入式电容电流检测结构的参数设计，并验证了其非侵入特性。应用该方案进行Buck变换器滞环控制，实验结果验证了非侵入式电容电流检测的动稳态性能和所提滞环控制的快速动态性能。

［1］Kapat S,Krein P T.Improved time optimal control of a buck converter based on capacitor current［J］.IEEE Transactions on Power Electronics，2012，27（3）：1444-1454.

［2］Meyer E，Zhang Zhiliang,Liu Yanfei.An optimal control method for buck converters using a practical capacitor charge balance technique［J］.IEEE Transactions on Power Electronics，2008，23（4）：1802-1812.

［3］Tan S C,Lai Y M.Constant-frequency reduced-state sliding mode current controller for Cuk converters［J］.IET Power Electronics，2008，1（4）：466-477.

［4］Tan S C，Lai Y M，Tse C K,et al.A fixed-frequency pulsewidth modulation based quasi-sliding-mode controller for buck converters［J］.IEEE Transactions on Power Electronics，2005，20（6）：1379-1392.

［5］Liu Changjin，Xu Dehong，Zhu Nan，et al.DC-voltage fluctuation elimination through a DC-capacitor current control for DFIG converters under unbalanced grid voltage conditions［J］.IEEE Transactions on Power Electronics，2013，28（7）：3206-3218.

［6］Li Xiaoqiang，Wu Xiaojie，Geng Yiwen，et al.Wide damping region for LCL-type grid-connected inverter with an improved capacitor-current-feedback method［J］.IEEE Transactions on Power Electronics，2015，30（9）：5247-5259.

［7］Huerta S C，Soto A，Alou P，et al.Advanced control for very fast DC-DC converters based on hysteresis of the current［J］.IEEE Transactions on Circuits and Systems I：Regular Papers，2013，60（4）：1052-1061.

［8］Huerta S C，Alou P，Oliver J A，et al.Design methodology of a non-invasive sensor to measure the current of the output capacitor for a very fast non-linear control［C］.Applied Power Electronics Conference and Exposition，2009：806-811.

［9］曹凯,姜建国,赵剑飞.带有滤波电容电流补偿的风电并网逆变器控制［J］.电源学报,2011,9（5）:56-59. Cao Kai,Jiang Jianguo,Zhao Jianfei.Control of grid-connected wind power inverter with current compensation in filter capacitor［J］.Journal of Power Supply,2011,9（5）:56-59（in Chinese）.

Design and Application of the Non-invasive Capacitor Current Sensing Circuit Based on Transfer Function Matching

YANG Yidi,LU Weiguo,ZHOU Luowei
（State Key Laboratory of Power Transmission Equipment&System Security and New Technology, Chongqing University,Chongqing 400044,China）

This paper discusses a simplified non-invasive current sensing circuit for an electrolytic capacitor.With a matching of the two transfer functions respectively for the sensing and sensed capacitor branches,the sensing circuit parameters are determined under non-invasive working condition.With an application of the proposed sensing circuit scheme to a capacitor-current based hysteretic controlled Buck converter,accuracy sensing for capacitor currents are achieved,as shown in the steady-state experimental waveforms.Furthermore,load transition experimental results verify the superiority of the proposed hysteretic control scheme.

non-invasive;capacitor-current sensing;Buck converter;hysteretic control;transfer function

杨异迪

杨异迪（1991-），男，通信作者，硕士研究生，研究方向：开关功率变换器的控制，E-mail：yangyidi@cqu.edu.cn。

卢伟国（1977-），男，博士，副教授，博士生导师，研究方向：开关功率变换器系统及控制技术，E-mail：luweiguo@cqu. edu.cn。

周雒维（1954-），男，博士，教授，博士生导师，研究方向：电力电子技术、电路理论及应用等，E-mail：zluowei@cqu.edu. cn。

10.13234/j.issn.2095-2805.2017.1.173

：TM 46

：A

2015-12-08