双容水箱模糊Smith时滞补偿控制系统混合实验平台设计

蒋建波， 苗爱敏， 李 鹏， 梁竹关， 邹 勋, 檀 磊

(云南大学 信息学院，云南 昆明 650091)

双容水箱模糊Smith时滞补偿控制系统混合实验平台设计

蒋建波， 苗爱敏， 李 鹏， 梁竹关， 邹 勋, 檀 磊

(云南大学 信息学院，云南 昆明 650091)

设计了一个基于西门子S7-300PLC控制系统和双容水箱实验装置的混合实验平台，其涵盖了控制策略的仿真以及对实际对象的控制。该平台利用以太网和OPC通信，实现了控制器、被控对象及监测系统之间的数据互联传输，并以模糊Smith时滞补偿控制策略的应用验证为例，使得虚拟仿真和实际验证有机地融合在一起并能够灵活、快速地转换，提高了双容液位系统控制策略设计的可移植性，解决了系统设计和工程应用之间的脱节问题。

实验平台； 双容水箱； 液位控制； 模糊Smith控制器； OPC

多容液位系统是食品、药物、饮料、化工等过程工业中最常见的控制对象之一[1],其控制策略大多围绕水箱的液位进行控制[2-3]。由于多容液位系统是一个多变量、强耦合、非线性的复杂系统,且时滞现象特别严重,使得常规PID控制难以达到理想的控制效果,因此多容液位系统成为工业过程控制领域研究和设计的技术难点[4]。

目前,研究多容液位控制系统的实验方法主要有两类:一类是基于Matlab等各种仿真软件对多容液位系统的控制算法进行虚拟仿真验证[5]；另一类则是采购或自主研发多容水箱实验装置,对其顺序逻辑及控制策略进行系统验证。借助多容水箱实验装置的方法虽然能够较好地模拟工业现场的实际情况,但研发周期较长,也不易于灵活、快速地集成先进的控制算法,容错率低,操作失误等原因会导致设备使用寿命缩短。基于仿真软件的方法则不存在操作失误的风险,可以大胆地对控制策略进行反复验证,直至达到满意效果,但模型过于理想化,不利于工程实践。此外,目前的工业控制过程都是工程设计人员根据控制对象的运行过程和控制需求进行设计和编程,然后再到设备现场进行调试改进,这使得系统设计和工程应用之间仍然存在脱节问题[6]。

因此,本文基于双容水箱控制系统提出一种包含控制策略仿真和实际对象控制的混合实验平台,并以模糊Smith时滞补偿控制策略的实现为例,分别对控制策略进行虚拟仿真验证以及实物现场的调试验证。通过以太网和OPC通信,实现了将虚拟仿真和实际验证有机地融合在一起,提高了控制系统设计的可移植性,解决了系统设计和工程应用之间的脱节问题,对工程设计人员进行现场调试和控制策略的验证具有重要借鉴意义。

1 混合实验平台简介

本文设计的混合实验平台组成见图1。该平台包含上位监控计算机和操作面板(监测系统)、虚拟仿真计算机(虚拟对象)、以太网交换机、西门子S7-300 PLC(控制器)和水箱系统(被控对象)。

图1 混合实验平台

上位监控计算机基于西门子综合平台软件Simatic Manager、编程软件STEP7和人机界面组态软件WinCC flexible搭建而成,主要作用是控制系统的硬件组态、人机界面组态、控制程序编制和动态监控水箱控制系统的控制过程,获取必要的过程数据与参数,也可以对控制系统中的一些过程参数或设定值进行人工设定。

虚拟仿真计算机基于Matlab软件和WinCC软件搭建,主要作用是对控制系统进行建模与仿真,模拟实际控制系统的各种过程参数,同时也可以对所提出的控制策略进行调试与验证。西门子S7-300PLC支持OPC通信,通过专用OPC服务软件WinCC实现虚拟对象系统与PLC之间的数据交互[6],在不接外设等情况下即可完成对控制策略的调试与验证。

操作面板为西门子TP177B彩色触摸屏,提供了人机交互的功能,可监测系统运行状态,也可以实现控制参数的设定、系统的启动停止、紧急制动等。

双容水箱控制系统主要由上水箱、下水箱、储水箱、抽水泵、三相电动机、水压表PS、压力传感器PT、电动调节阀EA、流量计FG,以及上下液位传感器LS1和LS2组成,整个水箱控制系统如图2所示。可分别选择水压、上、下水箱的液位作为被控对象,当选择上、下水箱的液位作为被控对象时只需保持水压恒定即可。

当选择水压作为被控对象时,由PLC、压力传感器、变频器和三相电动机共同组成一阶的闭环控制系统,以压力传感器的输出信号为反馈信号,PLC通过控制变频器的输出来调节三相电动机的转速,从而实现水压的平衡控制；当选择上水箱液位作为被控对象时,保持水压恒定,由PLC、上水箱液位传感器和电动调节阀共同组成一阶的闭环控制系统,以上水箱液位传感器的输出信号为反馈信号,PLC通过控制电动调节阀来调节水流量的大小,从而实现上水箱的液位平衡；当选择下水箱液位作为被控对象时,保持水压恒定,由PLC、下水箱液位传感器和电动调节阀共同组成二阶的闭环控制系统,以下水箱液位传感器的输出信号为反馈信号,PLC通过控制电动调节阀来调节水流量的大小,从而实现下水箱的液位平衡。

图2 水箱控制系统

液位传感器、压力传感器和电动调节阀直接与PLC的IO口连接,操作面板通过DP总线的方式与PLC相连,上位监控计算机、虚拟仿真计算机和变频器通过以太网的方式与PLC连接在一起,形成了一个完整的混合实验平台。该平台工作过程如下:

首先,进行控制策略的仿真验证。使用Matlab的Simulink仿真工具通过OPC通信实现虚拟仿真计算机与PLC的数据互联,以S7-300PLC为控制器,以虚拟仿真计算机中的系统传递函数模型为控制对象,利用所设计的控制策略进行仿真验证,通过不断的调试与参数调整,直至达到满意效果为止。

其次,将上述控制策略运用于水箱系统。该过程即为将虚拟的系统传递函数模型转换为真实的水箱模型的过程。以S7-300PLC为控制器,以双容水箱系统为控制对象,通过上述的控制策略对其进行控制,并通过上位监控计算机进行实时监控。

通过上述步骤即可实现从控制策略的调试与验证到将其应用于实际控制系统的无缝对接,解决了系统设计与工程应用之间的脱节问题。

2 控制算法设计

Smith算法由于其计算与控制的简便性,被广泛运用于解决滞后对象的控制问题[7]。但常规的Smith预估器需要基于精确的系统数学模型[8-10],在实际运用中系统参数时常会因干扰而变得不稳定[11],很难达到理想控制效果。模糊控制器无需被控对象的精确数学模型,因此考虑将模糊控制和常规Smith预估控制结合在一起构成模糊Smith控制器[12]。

本文选择下水箱液位作为被控对象,根据上述可知,该系统为一个二阶系统。在普通的Smith预估器的基础上加上模糊控制环节,可使得控制系统达到理想的控制效果。该控制系统的结构见图3。

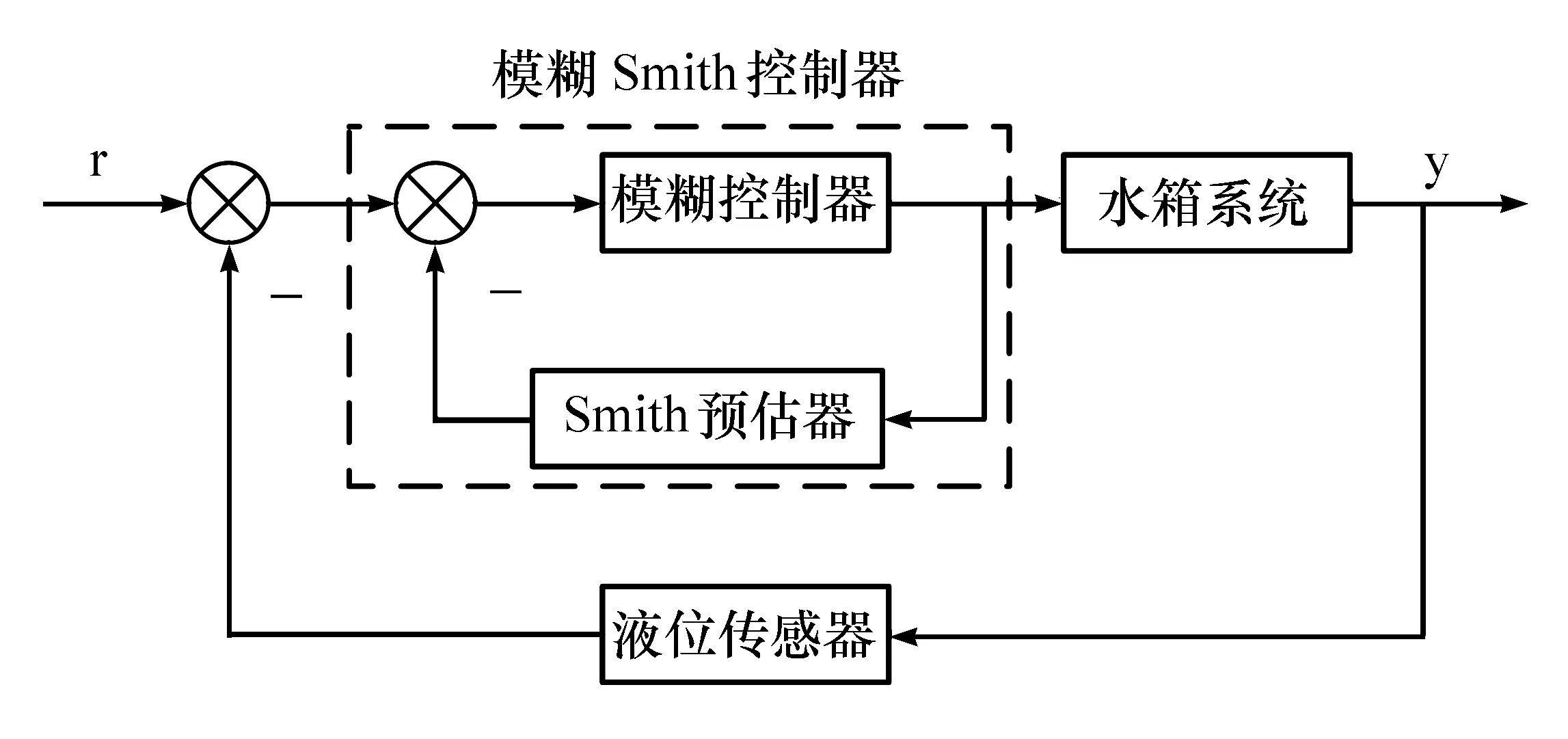
图3 模糊Smith控制系统结构

模糊Smith控制器的结构见图4(图中T为延迟时间)。采用目前运用比较广泛的二维模糊控制器,设定：输入综合偏差e的语言变量为E,相应的模糊子集定义为(NB,NM,NS,ZO,PS,PM,PB),论域为(-30,30)；偏差变化率ec的语言变量为Ec,相应的模糊子集定义为(NB,NS,ZO, PS,PB),论域为(-4,4)；输出量u的语言变量为U,相应的模糊子集定义为(NB,NM,NS,ZO, PS,PM,PB),论域为(-3000,3000),选择上述变量的隶属度函数均为三角函数。

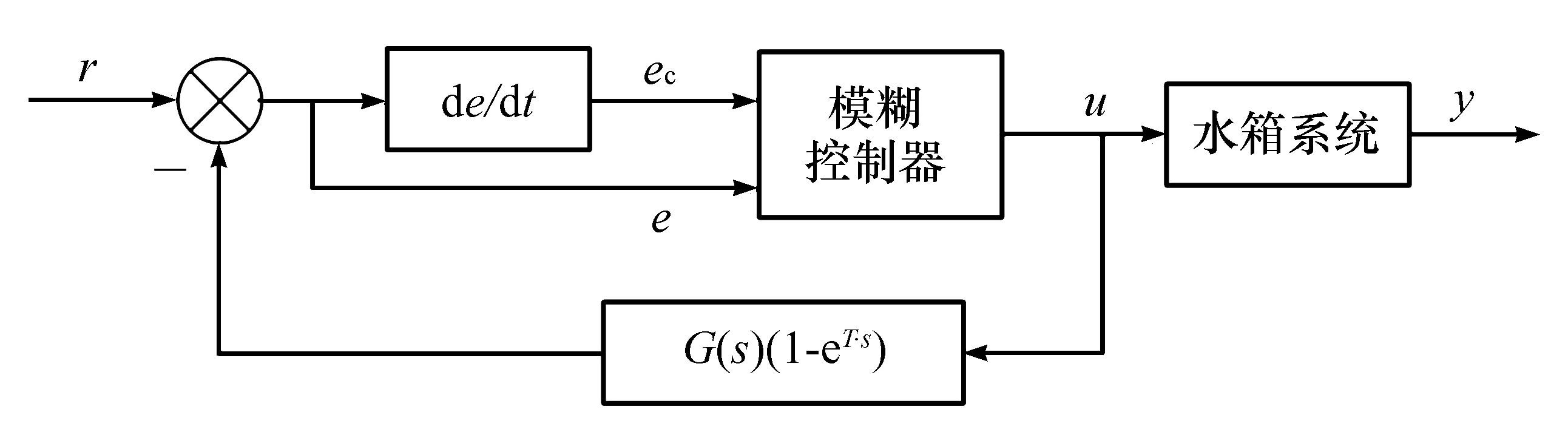
图4 模糊Smith控制器结构

根据现场实际控制情况对模糊规则进行调整,直至达到满意效果为止,最终达到如表1所示的模糊控制规则。

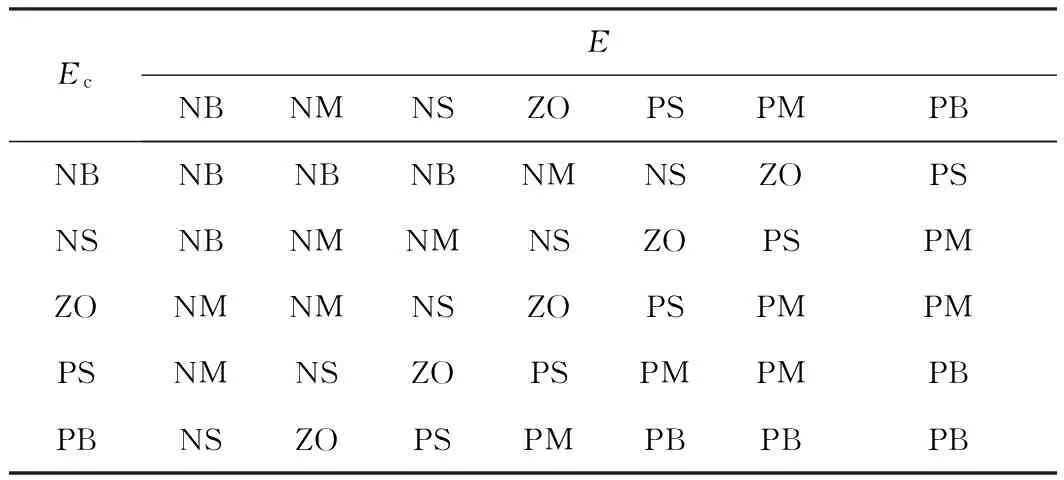
表1 模糊控制规则表

3 实验设计及仿真结果

3.1 基于仿真控制策略的实验设计

由于本文选择的控制对象是下水箱液位,该系统是一个二阶的带时滞的控制系统,需要利用设计的模糊Smith时滞补偿控制策略来对其进行控制。在将该控制策略运用到实际系统之前,需要使用Matlab的Simulink仿真工具对其进行仿真验证。

第一步,仿真过程需要对控制系统建立模型,运用系统辨识的方式,以阶跃信号为激励,采集被控系统的响应信号。通过Matlab的系统辨识工具箱对采集数据进行处理,得到被控对象的数学模型为

第二步,在Matlab的命令窗口中输入“fuzzy”,打开模糊工具箱,先分别定义输入综合偏差、偏差变化率和输出的论域和模糊子集,然后根据表1定义模糊控制规则如图5所示,定义完成后保存为.fis格式,最后使用readfis函数将其读入Matlab工作空间。

第三步,通过OPC工具建立Matlab与PLC之间的连接。由于WinCC本身就可以作为OPC通信方式的服务器,所以不需要做相应设置,由Matlab完成相应的设置即可,只需在WinCC中设置相应的过程变量和添加实时监测图即可。首先,在Matlab的命令窗口中输入“opcregister”完成对OPC服务的注册,注册之前需要将计算机中的opcEnum服务停用,否则会注册失败,注册成功后再重新启用opcEnum服务。其次,从OPC工具箱中拉出仿真需要的3个模块，即OPC Config、OPC Read和OPC Write。OPC Config的主要功能是设置Matlab与WinCC的OPC服务器之间的连接。OPC Read的主要功能是读取WinCC传送过来的设定值。OPC Write的主要功能是将仿真结果传送到WinCC中进行实时曲线的显示。最后,需要将WinCC的实时监控画面激活,通过OPC Config设置Matlab与WinCC的OPC服务器之间的连接,将OPC Read和WinCC中的设定值变量关联起来，将OPC Write和WinCC中的输出值变量关联起来。如果不激活WinCC,Matlab将无法与OPC服务器连接。

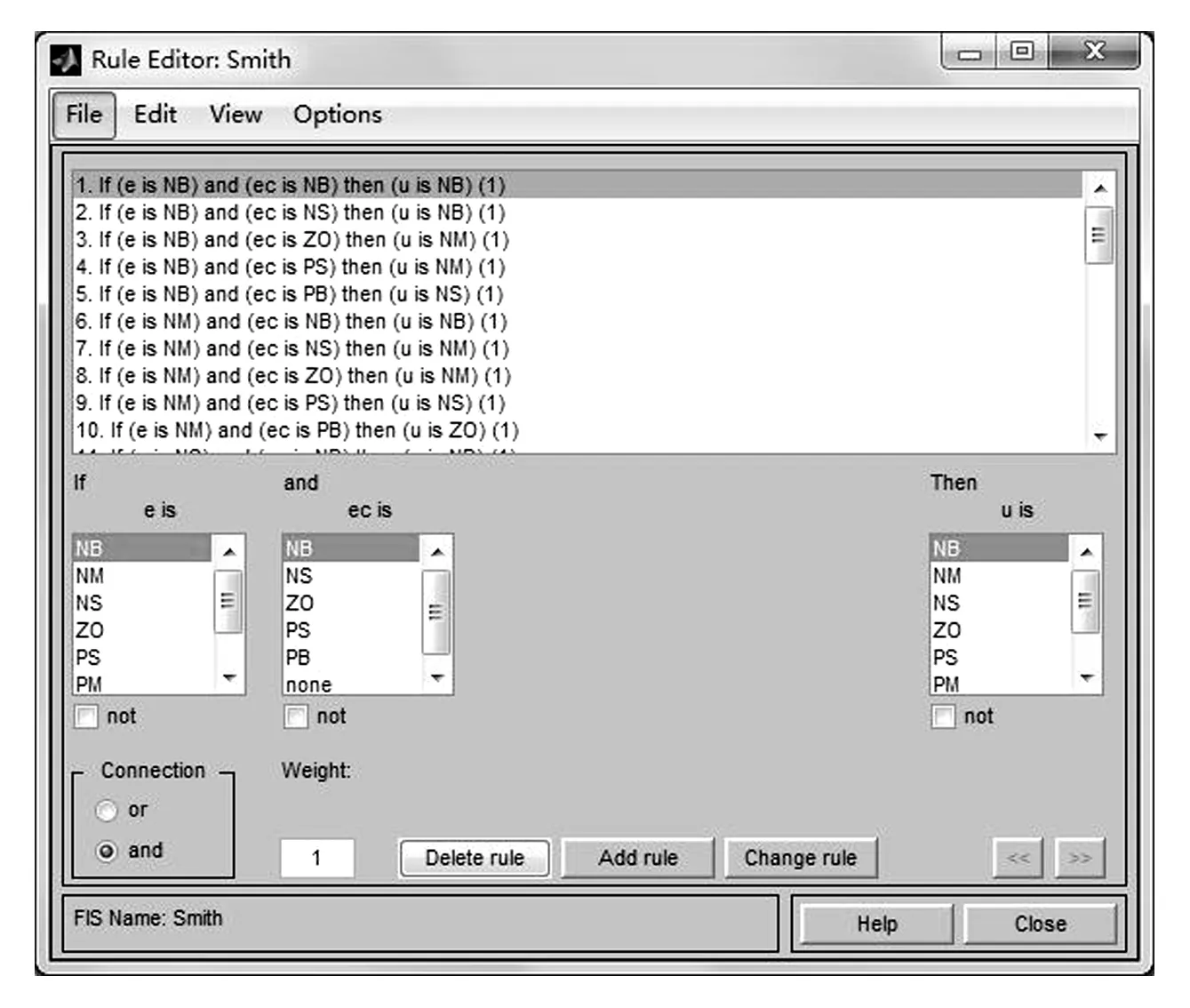
图5 模糊规则定义

第四步,将被控对象的数学模型、模糊Smith控制器、OPC Read和OPC Write连接起来(OPC Config不参与连接),即可形成最后的仿真模型,进而对控制策略进行仿真与验证。仿真框图见图6。通过WinCC对系统的设定值进行设定,同时对仿真过程进行监控。

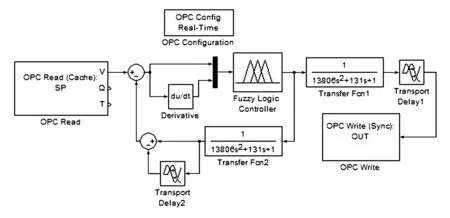
图6 Simulink仿真框图

该仿真的液位设定值为10 cm。图7为未加任何控制策略的仿真结果(图中h为液位),出现了较大的超调量和较大的稳态误差,稳定速度也较慢。图8加入模糊Smith控制策略后的仿真结果,系统的超调量极小、无稳态误差,而且能很快达到稳定状态。因此可以看出本文所设计的控制策略效果显著,性能优越。

3.2 基于控制实际对象的实验设计

在经过仿真控制策略的设计与调试验证之后,就可以将该控制策略应用于实际控制系统中。首先,使用上位监控计算机对整个PLC硬件系统进行组态,对使用的控制策略进行编程,对HMI操作面板进行组态并编辑人机交互界面,该界面包括实时过程值的显示框、设定值框、实时过程值曲线显示框、开始和停止按钮；其次,虚拟仿真计算机使用WinCC建立与PLC的连接,并进行实时过程值监控；最后,启动整个系统,对控制策略进行现场实物验证。

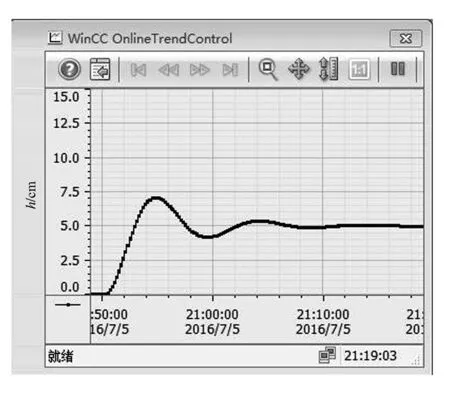
图7 未加控制策略的仿真结果

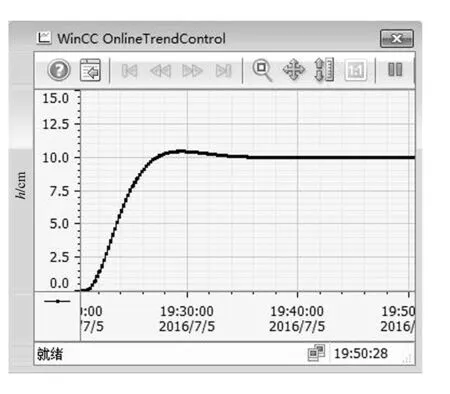
图8 模糊Smith控制仿真结果

由于编程软件STEP7中没有集成模糊控制模块和Smith预估器模块,因此需要对这2个控制模块进行自行编制。本文使用西门子S7-SCL语言进行编程,它是一种类似于PASCAL的高级语言,由于具有高级命令,将简化诸如循环和条件分支的编程,因此,ST-SCL 适合于方程、复杂优化算法，或大规模数据管理等的计算。由于STEP7默认支持梯形图和指令表编程方法,因此需要安装S7-SCL软件包方可进行程序编制。编译完成后,程序会被封装成功能(FC, Function)或功能块(FB, Function Block)的形式,在梯形图编程时可供调用。

Smith预估器的编程实现:由图4可看出，Smith预估器的核心就是将无时滞的响应信号和有时滞的响应信号进行相减,将相减后的结果作为模糊控制器的反馈信号。由于循环程序处理组织块是可以固定扫描周期的,因此可根据系统延迟与扫描周期的比例建立一个先进先出(FIFO)的变量队列,该队列用于存储延迟数据。由于本系统的延迟为40 s,因此在开始运行的前40 s内,该队列存储的数据都为0,从40 s开始以后该队列开始存储数据。S7-300 PLC默认扫描周期为100 ms,因此队列长度为400。由此就可以利用当前数据减掉队列里40 s以前的数据从而实现Smith预估器。核心代码如下:

…… TEMP_40S := DELAY_TEMP[1]; FORi := 1 TO 399 DO DELAY_TEMP[i] := DELAY_TEMP[i+1]; END_FOR DELAY_TEMP[400] := LIQUID_LEVEL; ……

其中,TEMP_40S为40 s以前水箱的液位测量值；DELAY_TEMP为长度为400的数组,用于存储FIFO队列中的数据；LIQUID_LEVEL为当前水箱的液位测量值。每经过一个扫描周期,就将数组的第一个元素DELAY_TEMP[1]的值赋给TEMP_40S变量,数组中的其余变量数值均往前移动1位,再将当前测得的液位值LIQUID_LEVEL放入数组的最后一个变量DELAY_TEMP[400]中,这样就实现了先入先出的队列。

模糊控制器的编程实现:模糊控制的原理就是根据误差和误差的微分的大小来决定模糊控制器输出值的大小。由于S7-SCL中没有微分运算,因此需要定义一个变量来记录上一个周期的误差,然后用本周期的误差减掉上一周期误差，再除以周期即可得到微分。根据表1中的模糊控制规则,使用IF语句来决定模糊控制器输出的大小,从而实现模糊控制器。核心代码如下所示:

…… E := SET_POINT-(LIQUID_LEVEL-TEMP_40S); EC := (E-TEMP_BEFORE)*10; TEMP_BEFORE := E; IF E <= -30 AND EC <= -4 THEN FS_OUTPUT := -3000; END_IF …… IF E>= 30 AND EC >= 4 THEN FS_OUTPUT := 3000; END_IF ……

其中,E为模糊控制器输入误差；EC为模糊控制器输入误差的变化率；TEMP_BEFORE为上一时刻的误差；FS_OUTPUT为模糊Smith控制器的输出。

将该程序编译封装成一个功能块(FB)。最后,在循环程序处理组织块OB1中用梯形图编程的方法调用模糊Smith控制器功能块,再加上启动和停止的程序段,整个程序就编写完成。

启动运行整个系统以后,通过上位监控计算机或者HMI操作面板给系统一个设定值(本次设定值为10 cm),然后观察水箱液位的变化,也可通过上位监控计算机、HMI人机交互界面或者虚拟仿真计算机的WinCC软件的监控画面对水箱液位的实时过程进行观测。通过WinCC观测的液位变化过程见图9。可以看出,该控制策略在现场实物控制过程中超调量极小,稳定时间较短,无稳态误差,稳定后虽然由于传感器误差及外交干扰等因素有小幅波动,但幅度不超过5 mm,达到了理想的控制效果。

图9 实物控制过程中水箱液位实时曲线

4 结论

本文设计的半实物、半仿真的混合实验平台,涵盖了从控制策略的仿真与验证到该控制策略在实物平台上的应用,通过OPC和以太网通信,该平台实现了控制器、被控系统、虚拟对象和监测系统之间的数据互联,针对双容水箱液位控制系统多变量、强耦合、非线性、大时滞的不确定性,采用了模糊Smith时滞补偿控制策略对其进行控制,既解决了时滞问题,又解决了普通Smith预估器需要精确数学模型的问题。使用表明，该平台具有准确、实用、方便、可靠等特性,解决了系统设计和工程应用之间的脱节问题,有助于设计人员对控制策略的调试验证与现场应用。

References)

[1] 朱涛,周天沛. 基于PLC的双容水箱液位控制仿真与实物实验系统设计[J]. 实验技术与管理,2013,30(11):29-33.

[2] 胡晓玮. 水箱液位PID控制系统研究[J]. 制造业自动化,2012,34(9):91-93.

[3] 王志刚,虎恩典,王宁. 基于PLC的双容水箱液位串级PID控制的实现[J]. 电子设计工程,2014,22(22):131-133,137.

[4] 田峰,王宏华. 大时滞系统的一种模糊-Smith控制[J].工业仪表与自动化装置,2004(1):36-38.

[5] 雷振伍,吴秀冰,孙德辉,等. 基于PCS7和Simulink的过程控制虚拟仿真实验平台开发[J].实验技术与管理,2016,33(1):135-139.

[6] 李鹏,孙鹤,张健,等. 电厂锅炉燃烧系统先进过程控制实验仿真平台[J]. 计算机与应用化学,2012,29(10):1216-1220.

[7] 章家岩,钱宏,冯旭刚,等. 基于Smith预估补偿的连铸结晶器液位控制策略[J].中国机械工程,2012,23(16):1947-1951.

[8] 李广军,李晓东,曾安平. 模糊免疫PID-Smith控制器及其在液位控制中的应用[J].中国农机化,2010(4):74-77.

[9] Wu Lianghong, Wang Yaonan, Zhou Shaowu, et al. Design of PID controller with incomplete derivation based on differential evolution algorithm[J]. Journal of Systems Engineering and Electronics, 2008,19(3):578-583.

[10] Zhou Hanqin, Wang Qingguo, Liu Min. Modified Smith predictor design for periodic disturbance rejection[J]. ISA Transactions, 2007, 46(4):493-503.

[11] 刘明朗,杜随更,郭扭,等. 基于改进Smith预估的液压伺服振动控制仿真[J]. 航空精密制造技术,2013,49(3):16-18.

[12] 王飞,石红瑞. 模糊Smith控制在PLC的实现及应用[J].控制工程, 2012(19):94-96.

Design of mixed experimental platform for fuzzy Smith time-delay compensation control system of double-capacity water tank

Jiang Jianbo，Miao Aimin，Li Peng，Liang Zhuguan，Zou Xun，Tan Lei

(School of Information, Yunnan University, Kunming 650091, China)

A mixed experimental platform based on Siemens S7-300PLC control system and the experimental device for the double-capacity water tank is designed, which includes the simulation of the control strategy and the control of the actual object. By using the Ethernet and OPC communication, this platform realizes the data interconnection transmission between the controller, controlled object and monitoring system. Taking the application verification of fuzzy Smith time-delay compensation control strategy as an example, the virtual simulation and the practical verification can merge together organically and convert into each other flexibly and quickly, which improves the transportability of strategic designing for the double-capacity liquid level system control, and solves the disjointed problem between the system designing and engineering application.

experimental platform; double-capacity water tank; liquid level control; fuzzy Smith controller; OPC

10.16791/j.cnki.sjg.2017.01.020

2016-07-20

国家自然科学基金项目(61364024)；云南省科技计划应用基础研究项目(2014FB112)；云南大学“中青骨干教师”培养计划项目

蒋建波(1992—)，男，云南保山，硕士研究生，主要研究方向为工业过程控制系统建模及仿真，电力信息物理融合系统

E-mail：1169025982@qq.com

李鹏(1976—)，男，云南玉溪，博士，副教授，主要研究方向为电力系统可靠性分析与维护决策、工业过程控制与优化等.

E-mail：lipeng@ynu.edu.cn

TP273; TP391.9

A

1002-4956(2017)1-0084-06