基于表面质量的小型精密零件切削工艺优化*
余 斌, 潘江如, 黄 勇, 尹君驰
(1. 新疆工程学院 机械工程系, 乌鲁木齐 830023; 2. 中国矿业大学 机电学院, 江苏 徐州 221116)
机械工程
基于表面质量的小型精密零件切削工艺优化*
余 斌1,2, 潘江如1, 黄 勇1, 尹君驰1
(1. 新疆工程学院 机械工程系, 乌鲁木齐 830023; 2. 中国矿业大学 机电学院, 江苏 徐州 221116)
为了提高小型精密零件在切削过程中的表面加工质量,以小型精密零件的表面粗糙度为目标函数,设计并实施了一系列小型精密零件的切削加工试验.采用单因素试验法分析了切削深度、切削速度及供给量等工艺参数对目标函数的影响,运用多元线性回归分析法建立切削工艺参数与目标函数的关系模型,从而获得最佳工艺参数组合并进行试验验证.结果表明,切削速度与切削深度对表面粗糙度为负向影响,供给量为正向影响,经优化参数组合加工工件的表面粗糙度均匀性较好,产品表面质量得到了较大改善.
小型精密零件; 表面质量; 切削速度; 切削深度; 供给量; 单因素分析; 多元线性回归分析; 工艺优化
随着社会需求的增强以及科技的快速发展,各类小型精密机械产品的使用量越来越多,同时在航天、医疗、电子等领域对小型精密零件的设计与制造要求越来越高[1-2].在小型精密零件的切削加工过程中,表面的粗糙程度是衡量其质量好坏的一个重要指标[3],而切削的深度、速度以及进给量等加工参数是影响零件表面质量的主要因素[4].因此,在小型精密零件的切削加工过程中,如果通过改变上述这些影响因素获得最佳的组合工艺参数,则对于改善零件表面质量,提高产品的性能将具有十分重要的意义.
国内外对高性能精密零件进行了较多研究,使得复杂结构零部件在表面质量和特性参数控制方面都得到了提升[5].但相比一般尺寸的精密零件,小型精密零件因尺寸小、结构复杂、性能要求高等特点决定了其微细切削工艺与常规工艺有很大的差别,如刀具的选型和使用、加工顺序的优化、走刀路线的确定、加工余量的最小化等,这些对小型精密零件的加工都提出了更高的要求.本文以表面粗糙度为目标函数进行切削试验,分别采用单因素试验法和多元线性回归法分析并研究切削深度、切削速度及供给量对目标函数的影响,从而获得最佳的工艺参数组合.
1 试验方法与设计
1.1 试验方法
不论采用何种加工方法,在零件的表面总是会留下细微的刀痕,特别是小型精密零件表面在放大镜或显微镜下可观察到凹凸不平、交错起伏的槽痕,槽痕的深浅代表表面粗糙程度Ra,其估计经验公式[6-7]为
(1)
式中:K为常数;vc为切削速度;Dp为切削深度;ft为供给量.由式(1)可知,工件表面的粗糙度与切削深度、切削速度及供给量具有密切的联系,将式(1)两边同时取对数运算,得到它们之间的线性关系式[8-11],即
y=c1+c2vc+c3Dp+c4ft
(2)
式中:c1为常数;c2、c3、c4分别为切削速度、切削深度及供给量对目标函数的影响回归系数.
1.2 试验设计
本次试验数控机床选用MIKRON UCP710,主轴最大转速1 800 r/min,功率15 kW,最大供给速度20 m/min;精车刀具选用FETTE LW225;加工对象为6061铝合金.分别以切削速度vc、切削深度Dp及供给量ft为变量加工出不同质量表面的工件,然后由表面粗糙度测量仪器(哈尔滨量具刃具厂2205型表面粗糙度测量仪)对每个加工工件的表面进行粗糙度测量,并记录读值.试验数据与对应的表面粗糙度测量结果如表1所示;表面粗糙度平均值计算结果统计如表2所示.
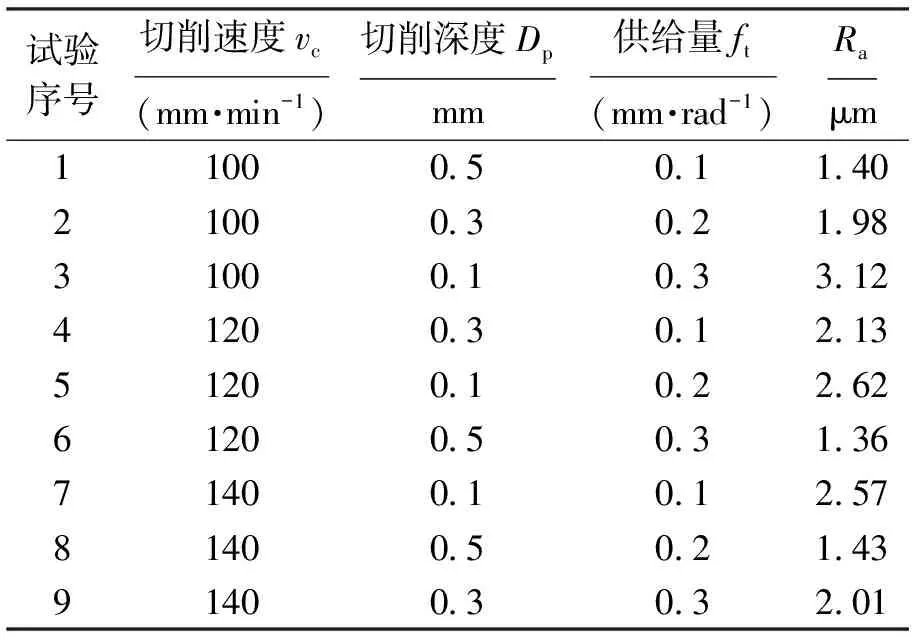
表1 试验数据与表面粗糙度测量结果Tab.1 Experimental data and measured results for surface roughness
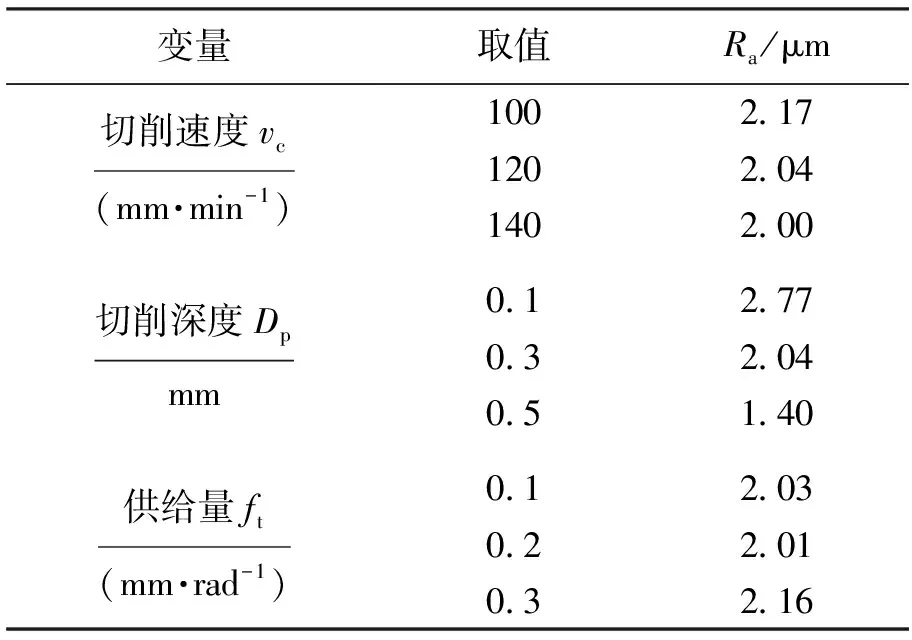
表2 各变量对应的表面粗糙度均值计算结果Tab.2 Calculated mean values of surface roughness corresponding to each variable
2 试验结果与分析
2.1 切削速度与表面粗糙度的关系
图1为不同切削速度对加工工件表面粗糙度的影响变化曲线.由图1可知,随着切削速度的增大,试验加工工件的表面粗糙度呈现出先急剧减小后基本稳定的变化趋势,即切削速度vc=120 mm/min为工件表面粗糙度较为稳定的临界点.
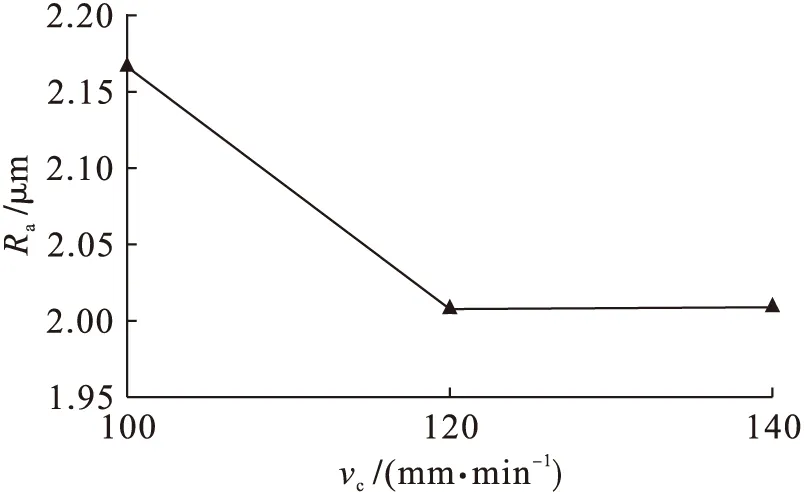
图1 切削速度对表面粗糙度的影响Fig.1 Effect of cutting speed on surface roughness
2.2 切削深度与表面粗糙度的关系
图2为不同切削深度对加工工件表面粗糙度的影响变化曲线.由图2可知,随着切削深度Dp的增大,试验加工工件的表面粗糙度呈逐渐减小的变化趋势.
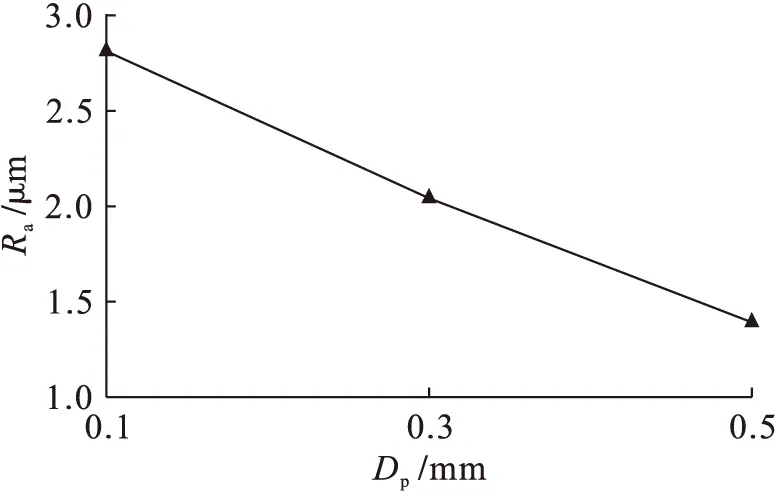
图2 切削深度对表面粗糙度的影响Fig.2 Effect of cutting depth on surface roughness
2.3 供给量与表面粗糙度的关系
图3为不同供给量对加工工件表面粗糙度的影响变化曲线.由图3可知,随着供给量ft的增大,试验加工工件的表面粗糙度呈现出先缓慢下降后快速升高的变化趋势,即供给量ft=0.2 mm/rad为工件表面粗糙度增大的临界点.
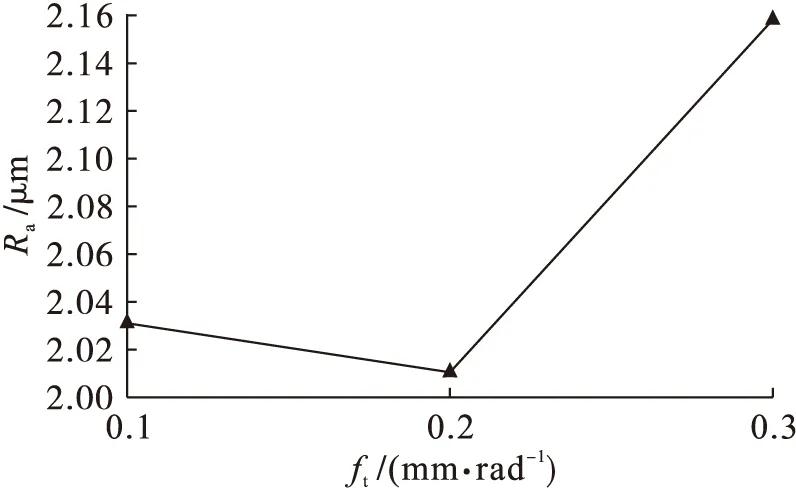
图3 供给量对表面粗糙度的影响Fig.3 Effect of supply quantity on surface roughness
2.4 SPSS多元线性回归分析
根据式(2)建立切削工艺参数与表面粗糙度的回归模型,由于模型中具有3个变量,为使模型的拟合优度最大,该模型调整的判定系数确定为0.938.回归分析平方和与均方差分别为2.457、0.801,剩余平方和与均方差分别为0.152、0.037,经F检测统计量的观测值为25.963,且对应的概率P<0.05,即满足建立线性模型的条件.表3为模型中各回归系数的分析结果,根据表3可知,切削速度对表面粗糙度具有负向影响,其影响回归系数为-0.005.切削深度和供给量对表面粗糙度的影响回归系数分别是-3.015、1.651,概率P值均小于0.05,即各变量对目标函数的影响作用均具有统计学意义.
表3 模型回归系数分析结果
Tab.3 Analysis results for model regression coefficients
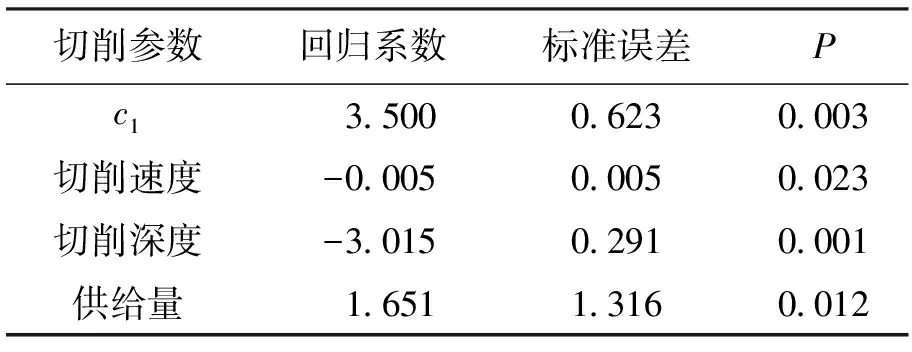
切削参数回归系数标准误差Pc1 3 5000 6230 003切削速度-0 0050 0050 023切削深度-3 0150 2910 001供给量1 6511 3160 012
将以上变量对表面粗糙度的影响回归系数代入式(2)中,可得多元线性回归方程式为
y=c1-0.005vc-3.015Dp+1.651ft
(3)
将式(3)作为本次加工工件表面粗糙度的预测模型,结合上述单因素对表面粗糙度的影响变化曲线分析可知,供给量ft对工件表面粗糙度的影响较小,特别是当供给量在0.1~0.2 mm/rad时,其影响几乎可以忽略不计.建立由切削速度、切削深度对表面粗糙度Ra相互影响关系的三维图形如图4所示.
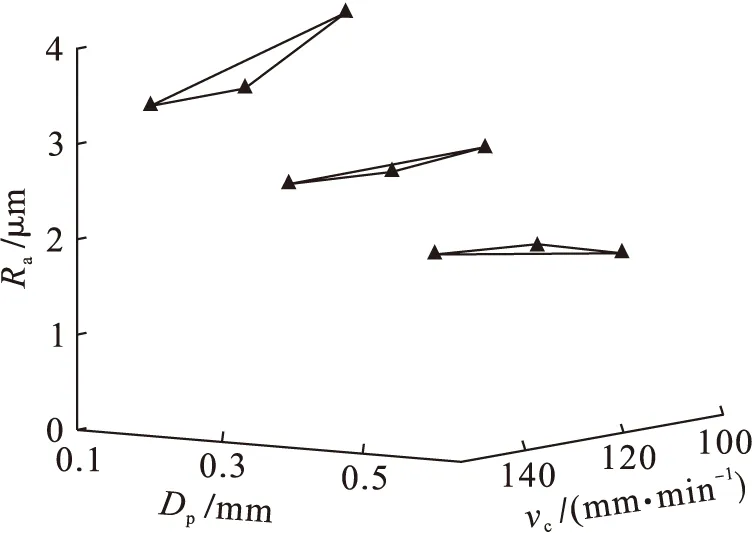
图4 切削速度、切削深度对表面粗糙度的影响Fig.4 Effect of cutting speed and depth on surface roughness
由图4可知,本次9组试验数据中,当供给量在0.1~0.2 mm/rad时,工件表面粗糙度最小时所对应的切削速度vc=100 mm/min,切削深度Dp=0.5 mm.以上述优化获得的最佳切削参数组合在数控机床上进行验证性精密切削试验,并分别对未经过优化和经优化工艺参数组合后的两组工件表面进行对比观察,结果如图5所示.结果显示,经优化切削工艺加工工件的表面粗糙度均匀性更好,预示其表面残余压应力一致性较好,从而验证了本次切削工艺参数优化的有效性.
3 结 论

图5 表面形貌特征比较Fig.5 Comparison in characteristics of surface morphologies
在试验数据设计范围内,通过对测试结果进行单因素试验法和SPSS多元线性回归法分析,研究了不同切削工艺参数对小型精密零件表面粗糙度的影响,得出如下结论:
1) 切削速度与切削深度对加工工件表面粗糙度的影响为负向影响,而供给量为正向影响,且供给量较小时对表面粗糙度的影响可以忽略不计;
2) 得出以表面粗糙度为目标函数,以切削速度、切削深度及供给量为主要变量的线性预测模型为y=c1-0.005vc-3.015Dp+1.651ft;
3) 本次以6061铝合金加工材料为例,通过试验证实了优化切削工艺参数有效性,预测模型达到了改善产品表面质量的目的.
[1]常智红.复合精密微切削加工系统设计与研究 [D].长春:长春理工大学,2010.
(CHANG Zhi-hong.Composite precision micro cutting system design and research [D].Changchun:Changchun University of Science and Technology,2010.)
(YU Bin-bin,YUAN Jun-tang.Study on integrated innovative technology of precision cutting and surface coating [J].Machnetool & Hydraulics,2010,38(23):5-8.)
[3]Onikural H,Ohnishi O.Fabrication of micro tools by
ultrasonic vibration grinding [J].Annals of the CIRP,2000,49(1):257-260.
[4]李文忠,胡玉景.超声磨削加工硬质合金材料的仿真分析 [J].青岛大学学报(自然科学版),2015,28(6):66-71.
(LI Wen-zhong,HU Yu-jing.Simulation analysis of ultrasonic vibration grinding of hard alloy [J].Journal of Qingdao University(Natural Science Edition),2015,28(6):66-71.)
[5]郭东明,孙玉文,贾振元.高性能精密制造方法及其研究进展 [J].机械工程学报,2014,50(11):119-134.
(GUO Dong-ming,SUN Yu-wen,JIA Zhen-yuan.Methods and research progress of high performance manufacturing [J].Journal of Mechanical Engineering,2014,50(11):119-134.)
[6]邢栋梁,张建华,沈学会,等.微细铣削铝合金表面粗糙度的实验研究 [J].制造技术与机床,2011(3):30-32.
(XING Dong-liang,ZHANG Jian-hua,SHEN Xue-hui,et al.Experimental study on surface roughness of aluminum alloy in micro-milling process [J].Manufacturing Technology & Machine Tool,2011(3):30-32.)
[7]王晓光,魏彩乔.硬车代磨表面粗糙度试验研究 [J].现代制造工程,2011(7):70-72.
(WANG Xiao-guang,WEI Cai-qiao.Experimental study on the surface roughness of dry turning of har-dened steel [J].Modern Manufacturing Engineering,2011(7):70-72.)
[8]曾其勇,吴凯,郑晓峰,等.影响切削工件表面质量的因素分析及要因的检测系统设计 [J].制造技术与机床,2012(4):108-111.
(ZENG Qi-yong,WU Kai,ZHENG Xiao-feng,et al.Factor analysis of workpiece surface quality and mea-suring system design for the main factors [J].Manufacturing Technology & Machine Tool,2012(4):108-111.)
[9]左健民,周少龙,汪木兰,等.基于SPSS软件的消失模表面质量数控切削工艺优化分析 [J].机床与液压,2014,42(5):24-27.
(ZUO Jian-min,ZHOU Shao-long,WANG Mu-lan,et al.CNC cutting process optimization for the surface quality of the EPS based on SPSS software [J].Machine Tool & Hydraulics,2014,42(5):24-27.)
[10]张承龙,冯平法,吴志军,等.旋转超声钻削的切削力数学模型及试验研究 [J].机械工程学报,2011,47(15):149-155.
(ZHANG Cheng-long,FENG Ping-fa,WU Zhi-jun,et al.Mathematical modeling and experimental research for cutting force in rotary ultrasonic drilling [J].Journal of Mechanical Engineering,2011,47(15):149-155.)
[11]贾平平.砂带磨削工艺参数的优化研究 [J].河南科学,2014,32(12):2511-2513.
(JIA Ping-ping.The optimization design of technolo-gical parameters about abrasive belt grinding [J].Henan Science,2014,32(12):2511-2513.)
(责任编辑:景 勇 英文审校:尹淑英)
Cutting process optimization of small precision parts based on surface quality
YU Bin1,2, PAN Jiang-ru1, HUANG Yong1, YIN Jun-chi1
(1. Department of Mechanical Engineering, Xinjiang Institute of Engineering, Urumqi 830023, China; 2. School of Mechanical and Electrical Engineering, China University of Mining and Technology, Xuzhou 221116, China)
In order to improve the surface machining quality of small precision parts in the cutting process, the surface roughness of small precision parts was taken as the objective function, and a series of cutting experiments for small precision parts were designed and implemented. The influence of such processing parameters as cutting depth, cutting speed and supply quantity on the objective function was analyzed with the single factor test method. With the multiple linear regression analysis method, the relationship model between the cutting parameter and objective function was established so as to obtain the best combination of processing parameters, and the experimental verification was carried out. The results show that the cutting speed and cutting depth have negative effect on the surface roughness, while the supply quantity has positive effect. After the combined machining with the optimization parameters, the uniformity of surface roughness of workpieces is better, and the surface quality of products gets greatly improved.
small precision part; surface quality; cutting speed; cutting depth; supply quantity; single factor analysis; multiple linear regression analysis; technological optimization
2016-03-29.
新疆科技厅高技术研究发展计划资助项目(201413105); 乌鲁木齐市科学技术计划资助项目(C151010004).
余 斌(1968-),男,新疆乌鲁木齐人,副教授,主要从事机械设计及先进制造技术等方面的研究.
16∶10在中国知网优先数字出版.
http:∥www.cnki.net/kcms/detail/21.1189.T.20160907.1610.048.html
10.7688/j.issn.1000-1646.2017.01.07
TM 343
A
1000-1646(2017)01-0034-04

