原始创新对经济增长贡献的省域空间差异

丁 刚，张柏秀

（福州大学经济与管理学院，福州350002）

原始创新对经济增长贡献的省域空间差异

丁 刚，张柏秀

（福州大学经济与管理学院，福州350002）

通过全局熵值法、BGWR（Bayesian Geographically Weighted Regression，贝叶斯地理加权回归）模型和基尼系数分解法的综合运用，对中国原始创新对经济增长贡献的省域空间差异进行了测度。研究结果表明：2010—2012年，中国省域原始创新能力总体呈增长态势，但在绝对水平和增长速度方面均存在一定的空间非均衡现象。平均而言，中国省域原始创新对经济增长的贡献率约为7．38%，东部地区高于中、西部地区，且在各省域间存在一定的空间差异。目前该差异主要表现为东、中、西部三大地区的区域间差异，三大区域内部所产生的差异对总体空间差异贡献度较小。

原始创新；经济增长；省域空间差异

引 言

作为自主创新的核心内容和根本要素，原始创新无疑对区域经济增长有着重要影响，区域原始创新能力与经济综合竞争力间存在着显著而密切的相关关系。为应对“后危机时代”的挑战，中国在把加快自主创新作为推动科学发展的战略抉择的同时，亦提出了实施区域发展总体战略，优化国土空间开发格局的目标。就原始创新对经济增长贡献的省域空间差异问题进行研究，对于上述战略目标的实现无疑具有重要的现实意义。

然而，经文献检索发现，即便技术进步是现代经济增长的内生演化动力这一观点已为学界所普遍接受，以原始创新对经济增长贡献空间差异为主题的研究成果迄今仍属鲜见，已有成果多集中于原始创新能力评价、原始创新对经济增长贡献的测度等方面。如，李海超等（2015）从人力资源投入、科研经费投入、环境支撑以及产出水平四个层面入手，构建了中国高科技产业原始创新能力评价指标体系，并运用熵值法对中国高科技产业原始创新能力进行了评价［1］；杨华峰等（2007）基于文献资料法、问卷调查法、专家访谈法的综合运用，从创新基础、科技投入、产出效益、环境支撑、持续创新五个层面入手构建了装备制造业原始创新能力综合评价指标体系［2］；李柏洲等（2010）从原始创新的投入能力、产出能力、核心能力、实施能力和环境支撑五个层面出发，构建了大型企业原始创新能力评价指标体系，并运用层次分析法对评价指标体系的权重进行了计算［3］；吴雷等（2012）基于索洛余值法建立了装备制造业生产函数模型，对1999—2009年中国装备制造业原始创新能力对经济增长的贡献率进行了实证分析［4］。

上述研究无疑积极且富有成效，但在方法论和研究视角上仍有进一步拓展的空间。一是在对原始创新能力进行评价时多运用层次分析法等主观赋权方法，以客观赋权及全局统一性、动态可比性为特征的全局熵值法等评价方法尚未得到充分应用；二是由于在研究视角中大多未纳入空间差异性，因而在进行区域原始创新对经济增长贡献率的相关测算时，往往忽略了空间变系数回归模型（Spatial Varying－Coefficient Regression Model）和基尼系数分解法等空间差异测度模型与方法的使用。

为此，本研究试图从省域层面出发，通过对全局熵值法、BGWR（Bayesian Geographically Weigh⁃ted Regression，贝叶斯地理加权回归）模型和基尼系数分解法的综合运用，对中国原始创新对经济增长贡献的省域空间差异进行测度，回答并理清下列问题：（1）中国省域原始创新能力的现状究竟如何？（2）当前原始创新对经济增长贡献的省域空间差异呈现何种特征？文章的第一部分，通过全局熵值法的应用对于中国30个省（市）区2010—2012年的原始创新能力现状进行了动态综合评价；第二部分通过BGWR模型的建构完成了省域原始创新对经济增长贡献率的实证测度分析过程；第三部分运用基尼系数分解法，就原始创新对经济增长贡献率的省域空间差异特征进行了分析探讨。

一、省域原始创新能力的动态综合评价

（一）评价指标体系的基本框架

在借鉴已有研究成果的基础上，遵循客观科学性、简明可得性、动态可比性等指标体系的构建原则，从原始创新能力的内涵出发，构建了涵盖科技支撑能力、科技投入能力、科技产出能力、环境保障能力等四个准则层，由29项指标构成的区域原始创新能力综合评价指标体系。其中，科技支撑（基础）能力主要反映原始创新活动的智力支持、经费支撑、研发条件等科技基础性要素禀赋状况；科技投入能力主要反映作为原始创新活动关键要素的基础研究领域人员和经费投入状况；科技产出能力主要反映原始创新活动的科技成果及其所产生的经济效益；环境保障能力主要反映除科技基础要素外，其他服务于原始创新活动的生态环保、社会保障、信息化建设等保障性要素状况，限于篇幅具体指标不一一列出。

（二）评价方法——全局熵值法

在评价研究领域，层次分析法、德尔菲法等主观赋权法的运用较为广泛，该类方法的固有缺陷是受人为因素影响较大，评价结果的可信度存在局限性。全局熵值法在熵值法的基础上扩展而来，在进行多指标综合评价时不仅能依据数据本身计算出信息熵，从而给各指标客观赋权，而且能使用面板数据从空间和时间的角度对评价对象进行全局动态分析［5］［6］。

（三）综合评价结果

基于《中国科技统计年鉴》（2011—2013）、《中国统计年鉴》（2011—2013）、《全国科技进步统计监测报告》（2011—2013），本文构造了2010—2012年中国各省域（不含西藏地区）的原始创新能力评价指标数据表。根据全局熵值法的具体实施步骤，首先对评价所涉及的原始指标数据进行了正向化、标准化处理。然后，用所得的无量纲数据计算出信息熵和相对应的评价指标权重。根据全局熵值法计算公式，可计算出各省域原始创新能力的综合评价得分，限于篇幅具体数值不再详列。

评价结果显示，2010—2012年中国各省域原始创新能力总体呈增长态势，但亦表现出一定的空间非均衡特征。平均而言，在反映绝对发展水平的原始创新能力综合评价得分上，东部地区较高（均值为 28．63），西部地区次之（均值为16．17），中部地区较低（均值为15．23）。但在反映相对发展水平的原始创新能力综合评价得分年均增速上，却呈现中部地区较高（9．62%），东部地区次之（8．13%），西部地区较低（6．83%）的发展格局；全国平均水平为7．86%，低于同期全国GDP年均增速（8．5%）。在东、中、西部三大地区之间存在差异的同时，各地区内部亦存在着一定程度的不均衡现象，以东部地区综合评价得分均值为例，最高值（81．89）与最低值（12．53）之间差异明显。

二、省域原始创新对经济增长贡献的实证分析

不言而喻，原始创新是技术进步的基础性动力。依据索洛（1956）开创的总量分析方法［7］，遵循内生经济增长理论关于区域技术进步对经济增长贡献的实证分析路径，本文采用将原始创新能力要素引入柯布—道格拉斯总量生产函数［8］（形如式（1）所示）的分析思路，运用BGWR模型达成省域原始创新对经济增长贡献的实证分析目的。

式（1）中，Yi、Li、Ki、Zi分别表示第 I＝省的国内生产总值、劳动力要素投入量、资本要素投入量和原始创新能力要素水平，Ai则表示除原始创新能力要素外其他影响技术进步的因素，μi代表着随机干扰项的影响，γ分别为劳动力要素、资本要素、原始创新能力要素的产出弹性系数。γ可通过对式（1）两边取对数，代入相应变量的观测值经计量模型运算求解得到，具体如式（2）所示。计算出γ的具体数值后，将其代入式（3），即可求出原始创新能力要素对经济增长的贡献率。

由于不同省域原始创新能力要素的产出弹性系数在空间上可能各异，因而在对γ求解时运用空间变系数回归模型（Spatial Varying－Coefficient Regression Model）应是合适的。本研究拟运用BGWR模型完成对γ的测算求解。

（一）BGWR模型简介

BGWR（Bayesian Geographically Weighted Re⁃gression，贝叶斯地理加权回归）模型是目前较流行且具权威性的一种空间变系数回归模型，基于后验分布采用吉布斯抽样（Gibbs Sampler）进行参数估计，可有效克服传统的GWR（Geographical⁃ly Weighted Regression，地理加权回归）模型在使用时所具有的本质缺陷［9］：一是仅使用最小二乘法难以实现对于回归参数的全面有效估计；二是由于观测值可能被孤立点（如周围临海岛屿）的离群值所“污染”，因而无法以线性回归形式实现准确估计；三是局部线性估计会遭遇“疲软数据（weak data）”问题。

BGWR模型的一般形式如式（4）－（5）所述：

式（4）中，y为由被解释变量观测值所构成的y矢量；x为由解释变量观测值所构成的n×k矩阵，βi为系数矩阵，ε为同方差、正态分布的随机扰动项。n×k代表一个n×n的距离权重对角矩阵。式（5）中的 wij为标准化距离权重，wij＝dij为观测点i和j之间的距离，θ为距离频宽（bandwidth）。在实际运用BGWR模型对βi等参数进行估计时，除（5）式所示的“距离平滑”法外，可以使用的平滑方法有两种：“单中心城市平滑”方法和“邻近平滑”方法。

考虑到本例中海南为周围临海岛屿，BGWR模型相对于GWR模型在实际估计时优势明显，故运用该模型测算原始创新能力要素的产出弹性系数γ。在实际测算时，被解释变量的观测值为观测期内（2010—2012年）各省域历年国内生产总值的平均值（为确保可比性，已将各年度的名义GDP统一折算为以1952年不变价格表示的实际GDP）。各解释变量观测值中，劳动力要素投入量为观测期内（2010—2012年）各省域历年年末从业人员数的平均值；资本要素投入量为观测期内（2010—2012年）采用张军（2004）方法［10］经计算整理而得到的各省域历年物质资本存量的平均值（1952年不变价格表示）；上述各变量的观测值均可根据《新中国55年统计资料汇编》、中经网和相关年份《中国统计年鉴》、分省统计年鉴计算整理得到。原始创新能力要素则由前文中观测期内（2010—2012年）各省域历年原始创新能力综合评价得分的平均值表示。通过三种方案的比较，即“距离平滑”方法、“单中心城市平滑”方法和“邻近平滑”方法的综合运用，选择后验概率最大的平滑方法估计结果作为所采信的最终方案。

测算过程借助MATLAB软件空间计量工具箱编程完成，采用高斯函数（Gaussian Distance）对于距离权重矩阵进行了选定，在实际运算过程中发现，无论运用何种平滑方法，所得BGWR计量模型的拟合优度均在0．98以上，且各变量的回归系数均通过了5%的显著性水平检验。具体测算结果如表1所示。从表1可以看出，最终方案采用了“单中心城市平滑”法的回归结果。根据中国东、中、西部地区各省域原始创新能力要素的产出弹性系数，按照要素贡献率计算公式（3）可进一步计算得到各省域原始创新对经济增长的贡献率，亦如表1所示。

表1 BGWR模型的测算结果

由表1中所列数据测算可以发现，全国范围内各省域原始创新能力要素的产出弹性系数的确存在一定差异，西部地区略高于中、东部地区，目前全国平均水平约为10．37%，这意味着在其他条件不变的情况下，平均而言中国省域原始创新能力要素每增长1%，约能带动省域经济总量增长0．1%。进一步的测算结果还表明，全国范围内各省域原始创新对经济增长的贡献率平均值约为7．38%，且这一贡献率在各省域间存在一定差异，东部地区均值（8．42%）略高于中部地区（8．39%），亦高于西部地区（5．61%）。为就原始创新对经济增长贡献率的省域空间差异问题进行更为深入地探讨，本研究引入基尼系数分解法来达成分析目的。

三、原始创新对经济增长影响的省域空间差异测度

（一）基尼系数分解法简介［11］［12］

基尼系数分解法是目前较为流行的一种空间差异测算法，被广泛应用于地区间、组群间的差距测算，其基本分解公式如下所示：

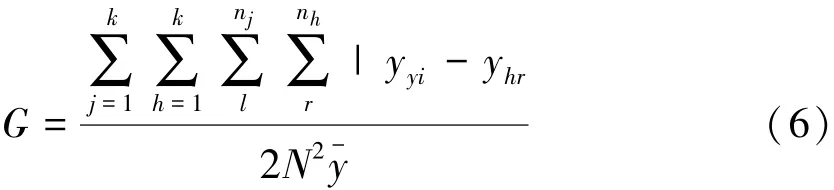
式（6）中，yji（yhr）分别表示j（h）地区中第i（r）个省域的某项待测指标值，y－表示其均值，N表示省域个数，k是地区划分个数，nj（nh）表示j（h）地区内省域的个数。

基尼系数可进一步分解为地区内差异对总体差异的贡献度Gw和地区间差异对总体差异的贡献度Gb，亦即G＝Gw＋Gb。其中，区域Pj内部的基尼系数为：

区域j和区域h之间的基尼系数计算公式为：

则区域j和区域h之间差异对总体基尼系数的贡献度为：

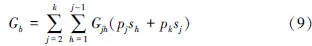
则区域j和区域h之间差异对总体基尼系数越大。

（二）基尼系数测算与分解结果

本例中，待测指标为省域原始创新对经济增长贡献率，指标值如表1所示。N＝30（省域个数为30）；因作东、中、西三大地区划分，故k＝3。基尼系数分解结果如表2所示。

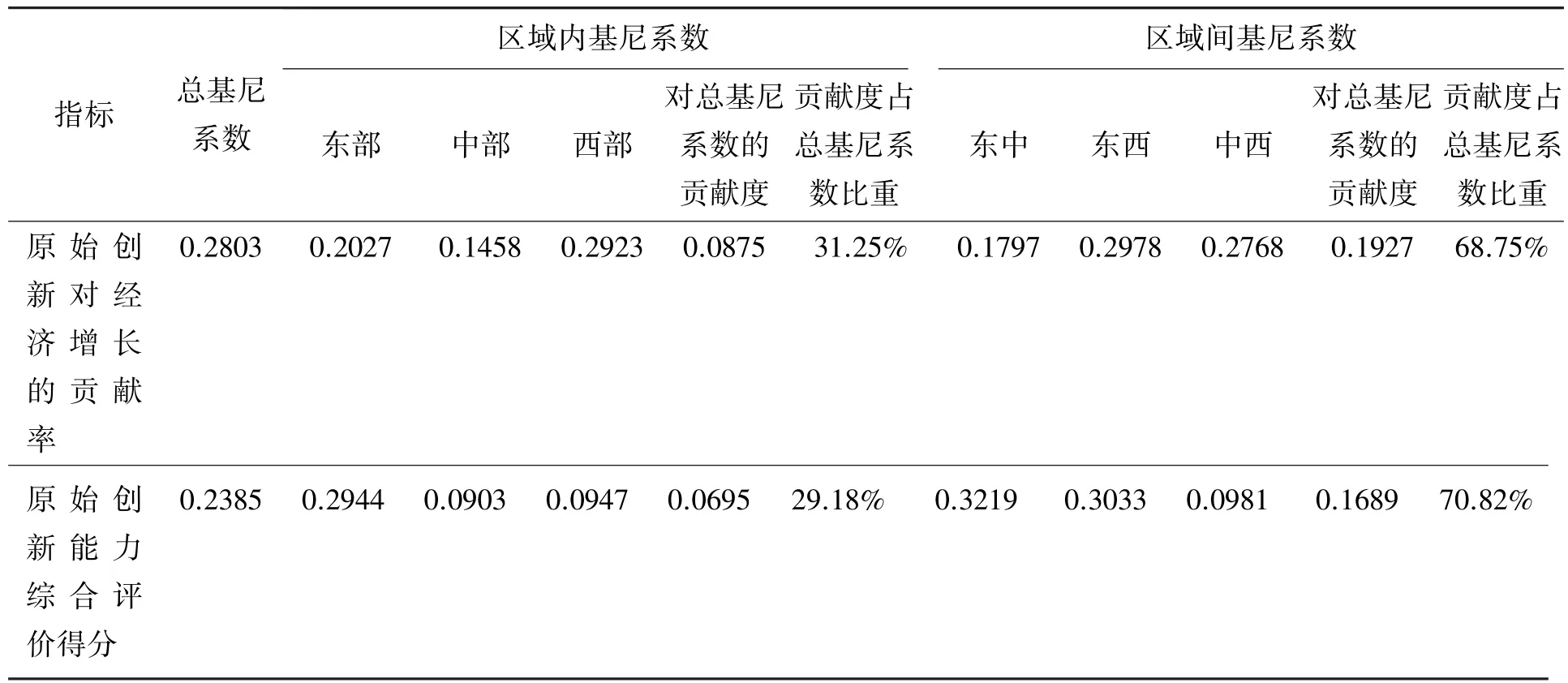
表2 省域原始创新对经济增长贡献率的基尼系数测算及分解结果

从表2中可以看出，中国省域原始创新对经济增长贡献率的总基尼系数为0．2803，其中区域内基尼系数对总基尼系数的贡献度为0．0875，在总基尼系数中占比为31．25%；区域间基尼系数对总基尼系数的贡献度为0．1927，在总基尼系数中占比为68．75%。这表明目前中国原始创新对经济增长贡献的省域空间差异主要表现为东、中、西部三大地区的区域间差异，而三大区域内部所产生的差异对总体空间差异贡献度较小。就东、中、西三大区域的原始创新对经济增长贡献率区域内差异情形而言，其区域内基尼系数分别为0．2027、0．1458和0．2923，表明当前西部地区的区域内差异最大，其次为东部地区，中部地区最小。就东、中、西三大区域的原始创新对经济增长贡献率区域间差异情形而言，东中部、东西部和中西部之间的区域间基尼系数分别为0．1797、0．2978和0．2768，表明当前东西部地区之间的差异最大，其次为中西部之间，东中部地区之间的差异最小。

为便于比较，除原始创新对经济增长贡献率这一指标外，表2中还列出了对中国省域原始创新能力综合评价得分均值的基尼系数测算及分解结果。经比较发现，前者的总基尼系数高于后者（0．2803＞0．2385），说明尽管中国省域原始创新能力亦存在着一定幅度的空间差异，但其非均衡程度仍低于原始创新对经济增长的贡献率；且由于两者的总基尼系数均小于0．4的警戒线水平，说明两者均未出现严重的空间非均衡发展现象。两者的区域内基尼系数测算结果显示，后者呈现出东部地区最高、西部地区次之、中部地区最小的发展情形，同前者西部地区最高、东部地区次之、中部地区最小的情形并不一致；两者的区域间基尼系数测算结果亦显示，后者呈现出东中部间的差异最大、东西部间差异次之、中西部之间差异最小的发展情形，而前者的测算结果则显示东西部地区之间的差异最大，其次为中西部之间，东中部地区之间的差异最小。尽管两者在基尼系数测算及分解结果方面存在上述差别，但亦有相似之处：东、中、西部三大地区区域间差异对总体空间差异的贡献率均显著高于其各自的区域内差异贡献率，均为70%左右。

结 论

第一，2010—2012年，中国省域原始创新能力总体呈增长态势，中部地区增速较高，东部地区次之，西部地区较低，但这一增速低于同期全国GDP增速，在某种程度上折射出中国当前经济发展方式的粗放型特征。当前中国省域原始创新能力表现出一定的空间非均衡特征，相较而言东部地区的原始创新能力较高，其次为西部地区，中部地区较低。其省域空间差异主要表现为东、中、西部三大地区之间的区域间差异，而三大区域内部所产生的差异对总体空间差异贡献度较小。就区域间差异而言，东、中部间的差异最大，东、西部间差异次之，中、西部之间差异最小。就区域内差异而言，东部地区的区域内差异最大，其次为西部地区，中部地区最小。

第二，在其他条件不变的情况下，平均而言中国省域原始创新能力要素每增长1%，能带动省域经济总量增长0．1%。平均而言，中国省域原始创新对经济增长的贡献率约为7．38%，且这一指标值在各省域间存在一定差异，东部地区高于中部地区，中部地区又高于西部地区。同原始创新能力的省域空间差异相若，原始创新对经济增长贡献的省域空间差异亦主要表现为东、中、西部三大地区的区域间差异，三大区域内部所产生的差异对总体空间差异贡献度较小。就东、中、西三大区域的原始创新对经济增长贡献率区域内差异情形而言，西部地区最大，其次为东部地区，中部地区最小。就东、中、西三大区域的原始创新对经济增长贡献率区域间差异情形而言，东、西部地区之间的差异最大，其次为中、西部之间，东、中部地区之间的差异最小。

第三，中国省域原始创新能力及原始创新对经济增长的贡献率均存在一定程度的空间差异，但两者的总基尼系数均小于0．4的警戒线水平。这一方面表明两者均未出现严重的空间非均衡发展现象，另一方面亦突显出当前中国区域原始创新能力“高地”建设的必要性。事实上，由于当前中国东部地区无论在省域原始创新能力综合评价得分，抑或在原始创新对经济增长的贡献率方面均显著高于中、西部地区，因而在原始创新能力建设层面继续倡导东部地区率先发展的方略应是十分必要的，有助于在全国范围内培育一个能显著发挥示范带动与空间溢出效应的原始创新增长极。同时，由于当前中国省域原始创新能力建设的空间差异主要表现为东、中、西部三大地区的区域间差异，三大区域内部所产生的差异对总体空间差异贡献度较小，为统筹区域原始创新能力建设进程，应将调控重点优先放在对区域间差异的统筹协调方面，其次才是三大地区的区域内差异。

第四，为防范中国省域原始创新能力及原始创新对经济增长的贡献率的空间非均衡分布情形在未来一段时期进一步加剧，除将调控重点优先放在东、中、西部三大地区区域间差异上之外，亦不应忽视对东、中、西部三大地区区域内差异的统筹协调。由于测算结果显示，东部地区原始创新能力的区域内基尼系数最高，西部地区次之，中部地区最小，故在对区域内原始创新能力差异进行调控时，应把重中之重放在东部地区；而在促进省域原始创新对经济增长贡献率的协调发展方面，由于西部地区在这一指标上的区域内基尼系数最高，东部地区次之，中部地区最小，故应把重中之重放在西部地区；两者的调控策略应有所区别，并不一致。

本文虽试图通过对全局熵值法、BGWR（Bayesian Geographically Weighted Regression，贝叶斯地理加权回归）模型和基尼系数分解法的综合运用，对中国原始创新对经济增长贡献的省域空间差异进行客观测度，但仍存在许多不足。如在对省域原始创新能力进行综合评价时，评价指标选择的全面性、科学性及评价方法的集成多样性等仍有待提升等，这亦为后续研究的进一步拓展指明了方向。

［1］李海超，张赟，陈雪静．我国高科技产业原始创新能力评价研究［J］．科技进步与对策，2015，1（1）：1－4．

［2］杨华峰，申斌 ．装备制造业原始创新能力评价指标体系研究［J］．工业技术经济，2007，26（11）：25－89．

［3］李柏洲，董媛媛．基于层次分析法的我国大型企业原始创新能力评价研究［J］．科技进步与对策，2010，1（1）：125－129．

［4］吴雷，曾卫明．基于索洛余值法的装备制造业原始创新能力对经济增长的贡献率测度［J］．科技进步与对策，2010，29（3）：70－73．

［5］孙玉涛，刘凤朝，李滨．基于专利的中欧国家创新能力与发展模式比较［J］．科学学研究，2009，27（3）：440－444．

［6］丁刚，陈倩．基于全局熵值法的区域现代服务业行业竞争力评价研究——以福建省为例［J］．中国石油大学学报：社会科学版，2013，29（6）：14－19．

［7］SOLOW R．A Contribution to the Theory of Economic Growth［J］．Quarterly Journal of Economics，1956，70：65－94．

［8］COBB C，DOUGLAS P．A Theory of Production［J］．AmericanEconomic Review，1928，18：139－165．

［9］丁刚．基于BGWR模型的区域创新能力建设中政府效能测评［J］．技术经济，2013，（4）：20－26．

［10］张军，吴桂英，张吉鹏．中国省际物质资本存量估算：1952—2000［J］．经济研究，2004，（10）：35－44．

［11］DAGUM C．Inequality Measures Between Income Distri⁃butions with Applications［J］．Econometrica，1980，48（7）：1791－1803．

［12］DAGUM C．A New Approach to the Decomposition of the Gini Income Inequality Ratio［J］．Empirical Economics，1997，（22）：515－531．

The Spatial Contribution Differences of China’s Provincial Original Innovation to Economic Growth

DING Gang，ZHANG Bai⁃xiu
（School of Economics and Management，Fuzhou University，Fuzhou 350002，China）

Through the integrated use of Global Entropy Value Method，Bayesian Geographically Weigh⁃ted Regression Model and Gini Coefficient Decomposition Method，China＇s provincial contribution of original innovation to economic growth is analyzed from the angle of spatial differences in this paper．The results show that China＇s provincial original innovation ability is enhanced rapidly from 2010 to 2012，and the disequilibri⁃um phenomena also exist in its absolute level and velocity．Meanwhile，it is found that China＇s average provin⁃cial contribution of original innovation to economic growth is about 7．38%．The average provincial contribution of original innovation to economic growth in Eastern Region of China is higher than those of others．It is the re⁃gional differences among Eastern Region，Central Region and Western Region that play a major role in explai⁃ning the spatial differences of China＇s provincial contribution of original innovation to economic growth，not the regional internal differences of these three regions．

original innovation；economic growth；provincial spatial differences

F061．5

：A

：1009－1971（2017）01－0121－07

［责任编辑：王春］

2016－08－03

国家社会科学基金青年项目“省域生态文明建设的绩效评价、标尺竞争效应与空间关联模式研究”（13CJL071）；福建省科学技术协会2014年科技思想库重大专项“福建省生态文明建设与发展问题研究”（FJKX－ZD1401）；福建省软科学项目“‘十三五’高新产业技术体系及小巨人发展研究”（2015R0105）

丁刚（1974—），男，河南开封人，副教授，硕士生导师，博士，从事区域经济研究；张柏秀（1991—），女，福建南平人，硕士研究生，从事区域经济研究。