基于XFlow的涡激振动压电能量收集数值研究

张 敏，谢玉林，雷 林，赖宇阳

(1.上海交通大学 机械与动力工程学院，上海 200240；2.重庆交通大学 航运与船舶工程学院，重庆 400074；3.树优信息技术有限公司，北京 100062)

基于XFlow的涡激振动压电能量收集数值研究

张 敏1，2，谢玉林2，雷 林2，赖宇阳3

(1.上海交通大学 机械与动力工程学院，上海 200240；2.重庆交通大学 航运与船舶工程学院，重庆 400074；3.树优信息技术有限公司，北京 100062)

基于格子波尔兹曼无网格方法，利用XFlow对低质量阻尼比的单圆柱进行了涡激振动的数值模拟，数值计算结果与实验结果吻合较好。利用XFlow与OpenModelica建立流-机-电耦合计算模型求解涡激振动与高斯定律联立方程，对涡激振动压电能量收集进行了数值分析，得到不同电阻下的电压及功率输出。通过对振幅及电压时程曲线的比较得到两者相位差的变化规律。结果表明：输出电压随着电阻的增大而增大，输出功率在特定来流速度和电阻时最大。

机电工程；XFlow；涡激振动；低质量阻尼比；压电能量收集

0 引 言

涡激振动的研究已经有几十年的历史，针对刚性圆柱的涡激振动问题，国内外的学者给出了大量的实验结果和分析模型，C.H.K.WILLIAMSON等[1]对涡激振动研究进行了总结和分析，并指出钝体的不同响应模式决定于质量阻尼系数，较低的质量阻尼系数具有更大的共振范围以及更高的振幅，这一特性更有利于进行涡激振动的能量收集。

压电能量收集技术是近年来研究的热点，众多学者对不同压电换能装置的能量收集进行了研究[2-3],H.D.AKAYDIN等[4]对一个直径为19.8 mm的空心圆柱加单悬臂梁压电装置进行了风洞试验研究，获得最大功率为0.1 mW。E. MOLINO-MINERO-RE[5]对一系列圆柱加单悬臂梁压电装置进行了水槽涡激振动能量收集试验，圆柱直径为8 mm时获得最大功率为0.31 μW。A. MEHMOOD等[6]对低雷诺数、高质量比的涡激振动压电能量收集进行了计算，获得的最大功率为10 μW。王军雷等[7]使用OpenFOAM对带有压电悬臂梁的圆柱及方柱的涡激振动问题进行了研究，并与试验进行了对比，指出升力系数随风速单调递增，圆柱与方柱发生锁定的速度不同。之后将开路电压方程与涡激振动方程耦合，分析了低雷诺数下电压的输出特性，当U*=5.6时，开路电压为8.42 V[8]。针对负载电阻R的研究表明，当R为特定值时，系统的分流阻尼最大，系统可以获得最高的输出功率[9]。文献[10]对置于钝体后的PVDF悬臂梁进行了数值研究，研究的重点是PVDF悬臂梁的大变形流固耦合计算问题，机电耦合跟流固耦合采用了分步计算，对钝体与悬臂梁的距离对输出电压的影响进行了分析。

设计了一种双压电悬臂梁装置，用来收集涡激振动的能量。首先使用XFlow进行了圆柱涡激振动的验证计算，之后利用XFlow与OpenModelica建立了涡激振动压电耦合计算模型，计算系统的能量收集特性及参数影响。

1 涡激振动数值计算验证

XFlow基于无网格/格子波尔兹曼方法(LBM, lattice boltzmann method)，用介观模型来模拟流体宏观行为，具有易于使用、无需网格、高效并行、边界条件处理简单、模拟精确等特点。其内置的结构求解器，以自然的方式允许完全的流固耦合分析。笔者使用XFlow进行圆柱涡激振动计算，计算域见图1。

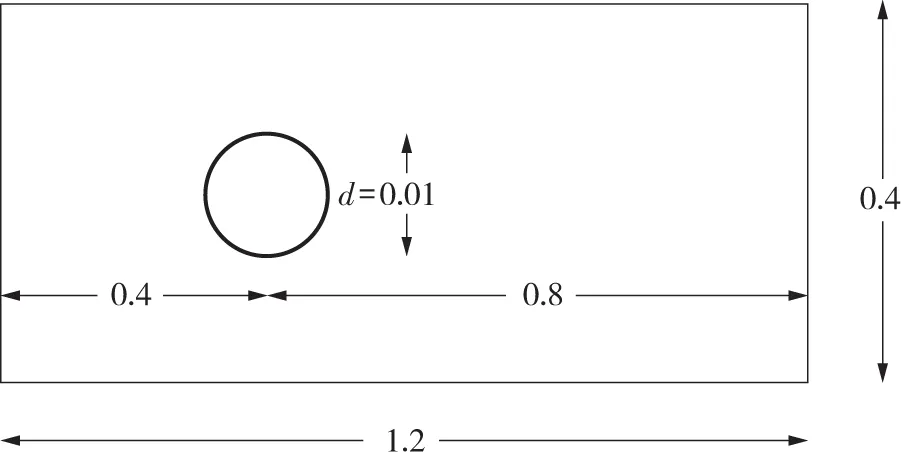
图1 计算域(单位：m)Fig.1 Computational region

圆柱涡激振动的运动微分方程可表示为：

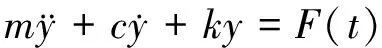
(1)

式中：m为圆柱质量；c为阻尼；k为刚度。各无量纲参数见表1。

表1 无量纲参数

计算参数选取如下：圆柱的直径D=0.01 m，质量比m*=1.19，固有频率fn=10 Hz，折合速度范围U*=4.0～20.0，雷诺数范围Re=4 000～20 000，水密度ρ=1 000 kg/m3，动力黏度系数μ=0.001 Pa·s，阻尼比ξ=0.005 02，计算域为1.2 m×0.4 m，坐标原点位于圆柱中心处，距离上游出口0.4 m，距离下游出口0.8 m，如图1。

将XFlow数值计算得到的振幅比、频率比随折合速度的变化规律R.GOVARDHAN & WILLIAMSON[11]的实验结果进行对比，如图2，图3。当U*在3～6，XFlow模拟得到的振幅和频率偏高；当折合速度在6～9，XFlow模拟得到的振幅符合实验结果并在折合速度为7.8时达到最大振幅比A*≈1，而频率相对偏低；当折合速度在9～12，XFlow模拟得到的振幅下降幅度与实验结果保持一致；当折合速度在12～16，振幅基本保持不变；在此之后，振幅继续呈现下降趋势，频率继续上升。计算结果与实验结果吻合得很好，结果表明XFlow可以很好地对低质量比，高雷诺数的圆柱涡激振动进行模拟。

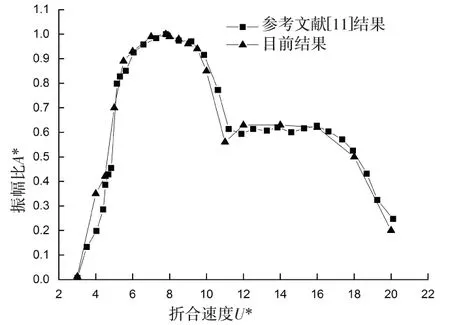
图2 振幅比随折合速度的变化规律对比Fig.2 Comparison of the variations of the amplitude ratio with the reduced velocity

图3 频率比随折合速度的变化规律对比Fig.3 Comparison of the variations of the frequency ratio with the reduced velocity

2 涡激振动能量收集

2.1 物理模型

笔者设计的能量收集装置是将两个压电悬臂梁固定到圆柱的横向位移自由度方向上，能量收集装置的原理如图4。其中c为系统的阻尼，k为系统刚度，y(t)为圆柱横向位移，Rl为等效负载电阻，U为来流速度。圆柱将在流场中产生的振动来带动压电悬臂梁振动产生电荷。压电能量收集装置的结构图以及电路连接如图5，图6。

图4 压电能量收集装置示意Fig.4 Schematic of the piezoelectric energy harvester

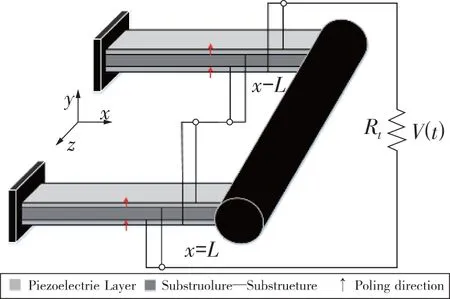
图5 压电能量收集装置Fig.5 Energy harvesting system with circuit,Fig.6

图6 压电悬臂梁剖视图Fig.6 cross-sectional view of a bimorph cantilever

2.2 数学模型

该系统的控制方程为弹性支撑的刚性圆柱振动与高斯公式[12]的耦合方程：

(2)

(3)

式中：θ为有效机电耦合系数；R为等效负载电阻；C为压电层的等效电容；V为等效负载电阻的电压。

上述参数的表达式为[13]

θ=2θp=e31(hp+hs)b

(4)

R=Rl

式中：Cp为单压电层的电容；θp为单个双晶悬臂梁的机电耦合系数；Rl为负载电阻；e31为压电常数；ε0为真空电容率；εr为相对电容率；hp，b和L分别代表压电层的厚、宽和长；hs为基层的高度。

在开路电压的分析中，令R=∞，由式(3)可得圆柱横向位移与开路电压Voc之间的关系：

(5)

开路时压电耦合可在形式上看成在原结构中附加了一个刚度项：

(6)

对于有负载电阻的情况，笔者使用XFlow与OpenModelica进行耦合计算。由XFlow计算圆柱所受的流体激振力F(t), OpenModelica编制的程序用来求解方程(2)、方程(3)，并将计算得到的圆柱位移y传回XFlow。对于开路情况，根据公式(6)在XFlow中设置涡激振动方程进行计算。

3 涡激振动能量收集计算

能量收集计算中，系统机电耦合系数θ=2.022e-4(V/N)，单压电层电容Cp=6.130e-8(F)。

图7，图8为带不同负载电阻与不带压电的振幅比与频率比变化规律的对比图。选取负载电阻分别为R=1e7 Ω，R=2e5 Ω，R=1e3 Ω。结果表明开路时系统的振幅与不带压电时的基本一致，频率比也没有显著的变化，由式(6)可知开路计算时，只是在方程中增加了一个较小的刚度项，因此系统的动力响应没有明显变化是合理的。当有电路连接负载电阻时，3个不同电阻的振幅在共振区域有不同程度的降低。当R=1e7 Ω时，最大振幅比A*=0.95；当R=2e5 Ω时，最大振幅比A*=0.9；当R=1e3 Ω时，最大振幅比A*=0.92。压电效应对本系统的动力响应的影响不强，振幅比与频率比分布规律相同。

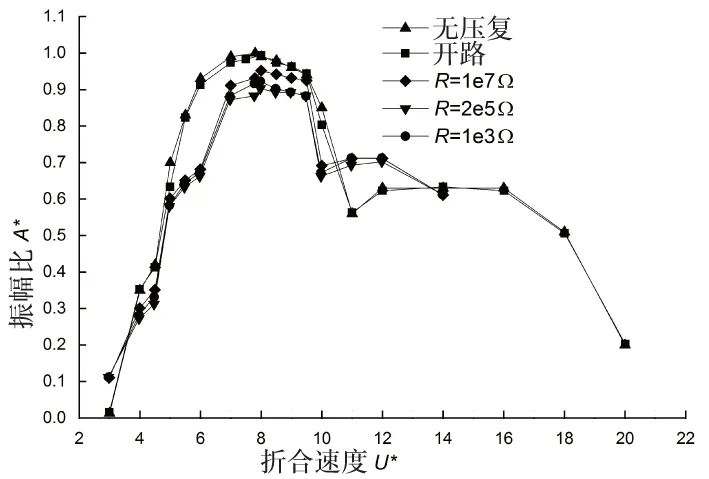
图7 不同负载电阻时的振幅比曲线Fig.7 Amplitude ratio curves for different values of load resistance

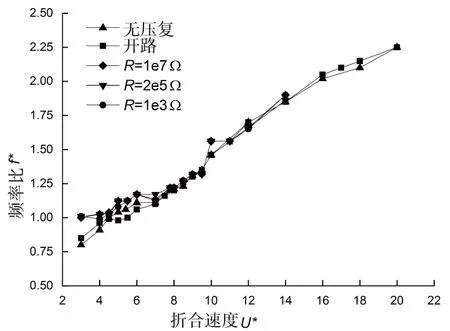
图8 不同负载电阻时的频率比曲线Fig.8 Frequency ratio curves for different values of load resistance

若假设圆柱的振动为正弦振动：

y(t)=A× sin ωt

(7)

式中：ω为振动频率，A为振幅。将式(7)代入式(3)并整理可得：

由式(8)可知负载电阻的电压幅值与系统的振幅、频率、机电耦合系数以及压电装置等效电容有关。对于特定结构，系统的等效电容及机电耦合系数固定，当电阻值一定时，系统振幅及振动频率相对稳定时，电压输出曲线应为平滑曲线。图9～图12为折合速度为4，8，10，14时不同电路连接的振幅以及电压输出时程曲线，分别位于锁定区域前、中、后的位置。随着折合速度的增加，振动频率随之增加，而振幅与电压先增大后减小。折合速度为4，14时，振幅并不稳定，这与涡街频率与系统固有频率差距较大有关；当折合速度为8，10时，系统振动相对稳定，特别在折合速度为10时，4种情况振幅与电压的输出曲线都比较平滑，而其它速度下除了开路情况，3个电阻的电压曲线尖峰处都出现不同程度的振荡。

由式(8)可知，振幅曲线与电压曲线之间的相位差除了与负载电阻、振动频率有关，还与压电装置等效电容有关。由图9，当折合速度为4时，开路情况下振幅曲线与电压曲线反相；R=1e7 Ω时，相位差约为0.009 πrad;R=2e5 Ω时，相位差约为0.31 πrad;R=1e3 Ω时，相位差约为0.5π rad。综合图9～图12可知：开路情况下，电阻无穷大，振幅与电压仅是反相；有负载电阻时，随着电阻的增大，相位差减小；同一电阻时，随着折合速度的增大或者振动频率的提高，相位差减小。

图9 U*=4时振幅和电压时程曲线Fig.9 Amplitude and voltage time traces when U*=4

图10 U*=8时振幅和电压时程曲线Fig.10 Amplitude and voltage time traces when U*=8

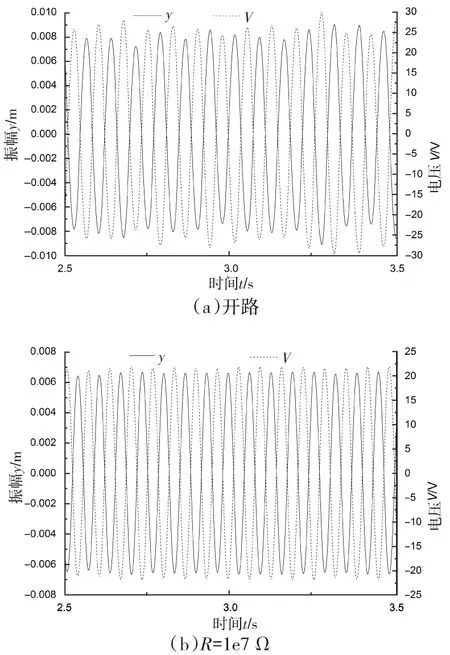
图11 U*=10时振幅和电压时程曲线Fig.11 Amplitude and voltage time traces when U*=10

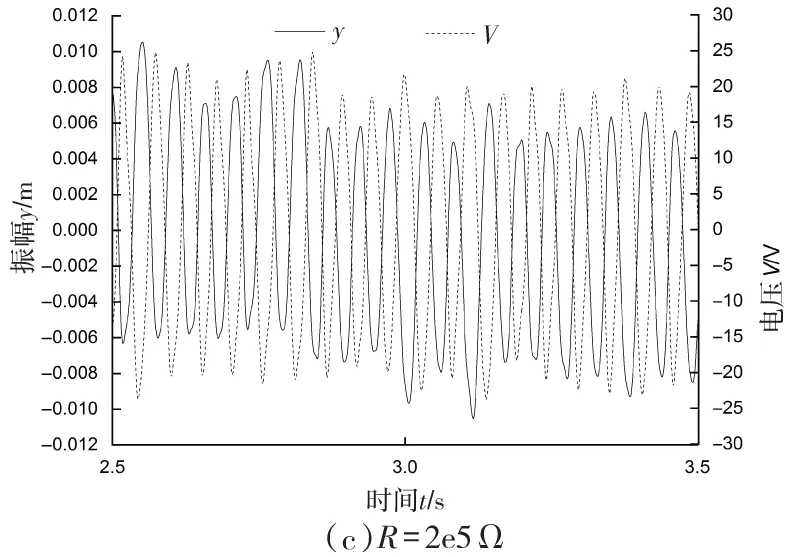
图12 U*=14时振幅和电压时程曲线Fig.12 Amplitude and voltage time traces when U*=14

开路以及3种负载电阻情况下，电压随折合速度的变化曲线如图13。折合速度为8时，即圆柱的振幅达到最大时，系统所产生的电压也最大，且随着电阻增大，电压也增大。当电阻R=1e7 Ω时电压与开路电压已较为接近；当电阻R=2e5 Ω时，最大电压由开路的32.5 V降低为21 V。

图13 不同负载电阻时的电压曲线Fig.13 Voltage curves for different values of load resistance

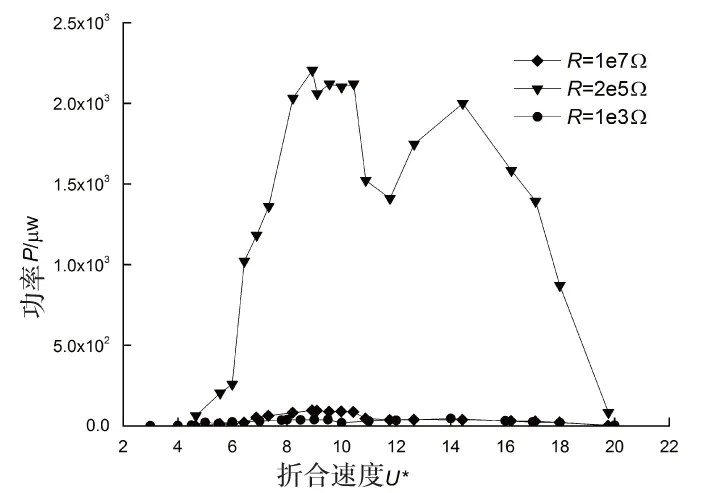
图14 不同负载电阻时的功率曲线Fig.14 Power curves for different values of load resistance

从图14可知系统电阻过大或电阻过小都会使功率减小，当电阻R=2e5 Ω时功率达到最大值2 205 μW。这是由于负载电阻要与压电材料的阻抗相匹配才能得到最高的输出功率[14]，因此在一个较窄的频率范围内，最大功率输出并不出现在输出电压最高的负载电阻上，而是有一个最佳负载电阻。

4 结 论

采用流体力学模拟软件XFlow对低质量比、高雷诺数下二维圆柱的涡激振动进行数值模拟，并与国外实验结果进行对比，然后计算了不同负载时的圆柱涡激振动压电能量收集情况，研究了不同负载下系统的动力响应以及电压、功率输出情况，得到如下结论：

1)根据Govardhan & Williamson实验参数对质量比为1.19，直径d为0.01 m的单圆柱在高雷诺数环境下进行了涡激振动的数值模拟，计算得到的振幅-速度曲线与实验吻合，振动圆柱振幅峰值出现的位置基本一致，说明利用XFlow对圆柱涡激振动进行数值模拟是可行的。

2)通过对带压电装置和不带压电装置圆柱进行模拟，并将两种情况下的圆柱涡激振动响应特性进行对比，发现带压电圆柱与不带压电圆柱的振幅及频率基本保持一致，只在有负载电阻时，振幅有较小的减少。说明本系统的压电效应对圆柱涡激振动的影响较小，在该系统中进行能量收集比较稳定。

3)通过对振幅及电压时程曲线的比较分析得到：开路情况下，振幅与电压反相；有负载电阻时，随着电阻的增大，相位差减小；同一电阻时，随着折合速度的增大或者振动频率的提高，相位差减小。

4)使用XFlow与OpenModelica建立了涡激振动压电能量收集的流-机-电耦合模型，得到了系统在不同负载电阻的工况下，振幅、频率、电压、功率随速度的变化规律。发现系统在负载电阻R=2e5 Ω，折合速度为7.8时系统获得最高的输出功率为2 205 μW。

[1] WILLIAMSON C H K, GOVARDHAN R. Vortex-induced vibrations[J].AnnualReviewofFluidMechanics, 2004，36(1)：413-455.

[2] 王青萍，王骐，姜胜林.压电能量收集器的研究现状[J].电子元件与材料，2012，31(2)：72-76. WANG Qingping, WANG Qi, JIANG Shenglin. Research status of piezoelectric energy harvester[J].ElectronicComponentsAndMaterials, 2012，31(2)：72-76

[3] 陈海俊，徐雅，孙大明，等.基于压电效应的时均流能量收集研究进展[J].低温工程，2013(1)：42-49. CHEN Haijun, XU Ya, SUN Daming, et al. Advances in mean flow energy harvesting using piezoelectric technology[J].Cryogenics，2013(1)：42-49.

[4] AKAYDIN H D, ELVIN N，ANDREOPOULOS Y. The performance of a self-excited fluidic energy harvester[J].SmartMaterialsandStructures, 2012，21(2)：025007.

[5] MOLINO-MINERO-RE E，CARBONELL-VENTURA M, FISAC-FUENTES C, et al. Piezoelectric energy harvesting from induced vortex in water flow[C]//Proceedingsofthe2012IEEEInternationalInstrumentationandMeasurementTechnologyConference, May 13-16， 2012.Graz, Austria: IEEE,c2012：624-627.

[6] MEHMOOD A, ABDELKEFI A，HAJJ M R, et al. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder[J].JournalofSoundandVibration, 2013，332(19)：4656-4667.

[7] WANG Junlei, RAN Jingyu, DING Lin, et al. 3-D dynamic simulation on fluid-structure interaction of air flowing around prism[C]// American Society of Mechanical Engineers[C]//PreceedingsoftheASME2014PowerConference, July 28-31，2014, Baltimore, Maryland, USA: ASME,c2014：V002T14A003.

[8] WANG Junlei, RAN Jingyu, ZHANG Zhien. Energy harvester based on the synchronization phenomenon of a circular cylinder[J].MathematicalProblemsinEngineering, 2014，2014(5)：1-9.

[9] 王军雷，冉景煜，张智恩，等.外界载荷对圆柱涡激振动能量转换的影响[J].浙江大学学报(工学版)，2015，49(6)：1093-1100. WANG Junlei, RAN Jingyu, ZHANG Zhien, et al. Effects of external load on energy conversion of vortex-induced vibrating cylinder[J].JournalofZhejiangUniversity(EngineeringScience), 2015，49(6)：1093-1100.

[10] 王军雷，冉景煜，丁林，等.基于涡激振动的压电能量收集特性数值研究[J].工程热物理学报，2015，36(2)：330-334. WANG Junlei, RAN Jingyu, DING Lin,et al. Numerical investigation of piezoelectric energy harvester characteristics based on vortex-induced Vibration[J].JournalofEngineeringThermophysics, 2015，36(2)：330-334.

[11] GOVARDHAN R, WILLIAMSON C H K. Modes of vortex formation and frequency response of a freely vibrating cylinder[J].JournalofFluidMechanics, 2000，420：85-130.

[12] ERTURK A, VIEIRA W G R, DE MARQUI C, et al. On the energy harvesting potential of piezoaeroelastic systems[J].AppliedPhysicsLetters, 2010，96(18)：184103.

[13] ZHANG Min, LIU Yingzheng, CAO Zhaomin. Modeling of piezoelectric energy harvesting from freely oscillating cylinders in water flow[J].MathematicalProblemsinEngineering, 2014：985360.

[14] 展永政，王光庆.压电振动能量采集器的性能分析与功率优化[J].浙江大学学报(工学版)，2014，48(7)：1248-1253 ZHAN Yongzheng, WANG Guangqing. Performance analysis and power optimization of piezoelectric vibration energy harvester[J].JournalofZhejiangUniversity(EngineeringScience), 2014，48(7)：1248-1253.

(责任编辑 朱汉容)

Numerical Research of Piezoelectric Energy Harvesting from VIV Based on XFlow

ZHANG Min1，2，XIE Yulin2，LEI Lin2，LAI Yuyang3

(1. School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240，P.R.China;2. Shipping and Marine Engineering College, Chongqing Jiaotong University, Chongqing 400074，P.R.China;3. Soyotec Limited, Beijing 100062，P.R.China)

The VIV numerical simulations of a circular cylinder with low mass damping ratio is done by using XFlow based on lattice Boltzmann meshless method. The numerical results are in good agreement with the experimental results. The fluid-mechanical-electric coupled model is established in XFlow and OpenModelica to solve the VIV and Gauss simultaneous equations. The output voltage and power of different values of load resistance are obtained through the numerical analysis. The change rule of the phase difference between the amplitude and voltage is obtained through comparing the amplitude and voltage time traces. The results show that the output voltage increased with the resistance load, the maximum output power can be obtained at a certain stream velocity and load resistance.

electromechanical engineering; XFlow; VIV; low mass damping ratio; piezoelectric energy harvesting

10.3969/j.issn.1674-0696.2017.01.19

2015-09-12；

2015-12-15

重庆市社会民生科技创新专项项目(cstc2015shmszx30031)；重庆市教委科学技术研究项目(KJ1705142)；重庆交通大学实验教学改革与研究基金项目(syjg201513)

张 敏(1982—)，男，山东人，讲师，博士研究生，主要从事计算流体力学、能量收集方面的工作。E-mail: zhangmin@cqjtu.edu.cn。

U661.1；TK 79；TN 384

A

1674-696(2017)01-103-07