三参数Weibull分布估计沥青混凝土疲劳失效研究

黎 晓，梁乃兴，程志豪

(1.云南省交通规划设计研究院 陆地交通气象灾害防治技术国家工程实验室，云南 昆明 650041；2.重庆交通大学 土木工程学院，重庆 400074)

三参数Weibull分布估计沥青混凝土疲劳失效研究

黎 晓1，2，梁乃兴2，程志豪1

(1.云南省交通规划设计研究院 陆地交通气象灾害防治技术国家工程实验室，云南 昆明 650041；2.重庆交通大学 土木工程学院，重庆 400074)

通过间接拉伸疲劳试验分析3种不同沥青混凝土材料在3种不同温度条件下疲劳失效特性。采用考虑形状参数、位置参数和尺度参数的Weibull分布函数对不同加载条件下材料疲劳寿命分布特征进行估计，提出了基于位置参数迭代计算下的特征参数估算方法，并给出了50%保证率下的材料疲劳寿命曲线和疲劳方程。研究结果表明：三参数Weibull分布函数可以避免在试验初始阶段进行疲劳失效概率的不合理估计，更好地预估小子样条件下材料疲劳失效分布；预估结果中特征参数项具有良好的线性相关性，三参数Weibull分布能较为清晰地反映出材料不同试验条件下的疲劳失效寿命分布。

道路工程；沥青混凝土；应力控制；三参数Weibull分布；疲劳失效估计

沥青混凝土材料的疲劳性能研究大多关注通过现象学方法获取材料寿命预估模型本身，对于试验中获取的材料疲劳寿命可靠性评估还未涉及较深入的研究。目前较多文献中已经采用概率统计方法对材料疲劳寿命试验数据进行分析[1-5]，以获取具有一定可靠度的寿命估计结果。

对于沥青混合料这类不均匀性材料，通过室内试验评估其疲劳性能是较为常见的方法。但是由于材料自身强度形成原因复杂，疲劳性能影响因素也较多，通过室内试验获取的数据结果往往呈现较大的不规则、离散性[6-10]。即便是温度、加载应力水平或加载频率等条件完全相同的情况下，试验结果也极有可能相差10倍或更高。若把相差一个数量级以上的试验结果采用“平均数”概念来处理必将导致极大的误差。所以有必要将沥青混凝土材料疲劳失效寿命视为随机变量用概率统计理论进行描述。

笔者通过考虑Weibull三参数分布的沥青混凝土疲劳失效寿命估计方法，对3种典型级配的沥青混凝土材料进行不同温度、不同应力水平下间接拉伸疲劳试验，对Weibull分布函数的位置参数等特征参数进行估计。在试验结果基础上，获取3种不同沥青混凝土材料的疲劳寿命特征分布函数，提出不同保证率下的材料疲劳寿命曲线及疲劳方程。

1 沥青混凝土间接拉伸疲劳试验

1.1 试验材料

以AC-13、AC-20和AC-25这3种典型沥青混凝土材料作为试验对象，试验中均采用设计级配中值进行材料设计。

沥青选用中海70#；集料采用本地产某采石场石灰岩；矿粉选用本地产石灰岩矿粉，经试验验证各材料性能均满足相应设计规范要求，混合料设计级配见表1。通过马歇尔试验结果确定出材料最佳沥青用量分别为4.8%(AC-13)、4.4%(AC-20)和3.8%(AC-25)，材料设计空隙率为4.3%(AC-13)、4.5%(AC-20)和4.7%(AC-25)。

表1 试验沥青混凝土级配组成

1.2 试验方案及试验条件

材料疲劳试验采用COOPER公司生产的CRT-NU-14气动伺服材料试验仪完成。该仪器配备的数据采集系统能自动采集传感器及位移计的电测信号，测量范围在1 μm～3 mm之间。

为分析不同温度条件下材料疲劳性能，试验采用应力控制模式加载，加载波形为半正矢波形荷载，加载频率10 Hz；根据不同温度条件下各级配的材料劈裂强度试验结果，选取应力比0.2～0.6之间各5种试验应力水平为加载应力强度，每个应力水平下进行4次平行试验。试验选定10，20，30 ℃这3种标准试验温度，试验研究中首先采用旋转压实方式完成试件制备，试验前所有试件均在温控箱内相应试验温度下保温4 h。

试验开始后在目标应力水平下进行循环加载，期间保持0.1 kPa的初始加载应力；其过程由计算机控制系统自动控制，并读取竖向力传感器和位移传感器数值，并按一定间隔时间自动记录试验数据。实时记录的试验数据包括：加载次数、应力值、竖向位移。本次试验中10，20 ℃条件下以试件开裂破坏判定为疲劳失效，30 ℃下以试件竖向变形时程曲线出现反弯点时作为疲劳失效判定标准[5]。

2 试验结果分析

2.1 试验结果

试验记录了3种沥青混凝土材料不同应力水平及温度条件下疲劳失效作用次数，由于篇幅所限，表2仅列出AC-13沥青混凝土材料试验结果。

表2 AC-13沥青混合料间接拉伸疲劳试验结果

2.2 Weibull失效分布函数

Weibull分布应用于沥青混合料疲劳失效估计中已经被部分研究文献证明是切实有效的[11-12]。但目前研究分析所采用的大多是双参数Weibull分布，双参数Weibull分布是三参数Weibull分布的一种特例。当沥青混合料试件疲劳失效概率服从三参数Weibull分布时，其分布函数为

(1)

式中：b为形状参数；Np为样本疲劳寿命；Na为特征疲劳寿命；N0为位置参数，可为简化为η=Na-N0，η为尺度参数；b>0，η>0，N0≥0。

三参数下Weibull分布的概率密度函数f(Np)为

(N0≤Np<∞)

(2)

式中：当b=1时，f(Np)为简单指数密度函数；当b=3～4时，f(Np)近似于正态分布密度函数。f(Np)曲线高峰的偏斜程度随形状参数b而变化，并存在大于0的最小值N0。

当假设位置参数N0=0时，式(1)～式(2)中分布函数即退化为双参数Weibull分布，以此对材料疲劳失效分布进行估计时，疲劳失效寿命是从0开始，不符合实际试验情况。而利用三参数Weibull分布估算材料疲劳失效，加入了位置参数N0，可避免在试验初始加载阶段进行疲劳失效概率的不合理估计，能更好地预估小子样的材料疲劳失效分布情况。

由式(1)可看出，传统双参数Weibull分布函数为非多项式函数，无法直接进行参数拟合，必须采用对式(1)的两次对数变量转换达到线性化的目的，如式(3)。

-lnln(1/p)=b[ln(Np-N0)-ln η]

(3)

式中：p=1-F(Np)为存活率。

根据概率分布理论，作为随机变量的破坏率是遵循某一频率分布的，无论被抽样母体为何种分布，小子样中某一样本xi破坏率的数学期望都可以采用“平均秩”作为小样本母体存活率的估计量[13]。将每个应力水平下的试件疲劳寿命按从小到大排列，对应第i个测定值xi的存活率p估计量可用式(4)计算：

(4)

式中：n为同批次样本总数。

则式(3)可写成式(5)：

(5)

对于三参数Weibull分布函数而言，位置参数N0是个未知值，从数值分布上来看其代表了沥青混凝土材料的最小寿命分布。若仍然采用上述方法直接求解将十分复杂，因此笔者采用迭代法来计算三参数Weibull分布函数的特征参数。

假设位置参数初始值为N0，根据式(3)和式(5)的函数形式可得到初始形状参数b1和尺度参数η1为

(6)

将式(6)代入式(1)，计算出位置参数：

(7)

式中：Npi即同一试验条件下第i组材料疲劳失效寿命，每一组疲劳失效寿命对应一个位置参数(N0)i，采用每一组迭代计算后的平均值作为其位置参数(N0)i。

式(7)可改写为

(8)

将得到的新的位置参数(N0)1代入式(3)，计算出新的形状参数b和尺度参数，并根据前述计算过程计算出该组样本下新的位置参数，直至相邻两次计算结果之差满足精度要求为止。

2.3 沥青混凝土疲劳失效寿命估计

基于上文所述理论编制相应程序进行不同温度、不同应力水平条件下各组材料寿命分布函数特征参数的计算。篇幅所限，表3为AC-13沥青混凝土材料三参数Weibull分布函数数值参数估计结果；图1、图2为AC-13和AC-20沥青混凝土在10 ℃温度条件下的4种应力水平下寿命分布特征参数相关性结果。

表3 沥青混合料疲劳失效分布函数参数(AC-13)

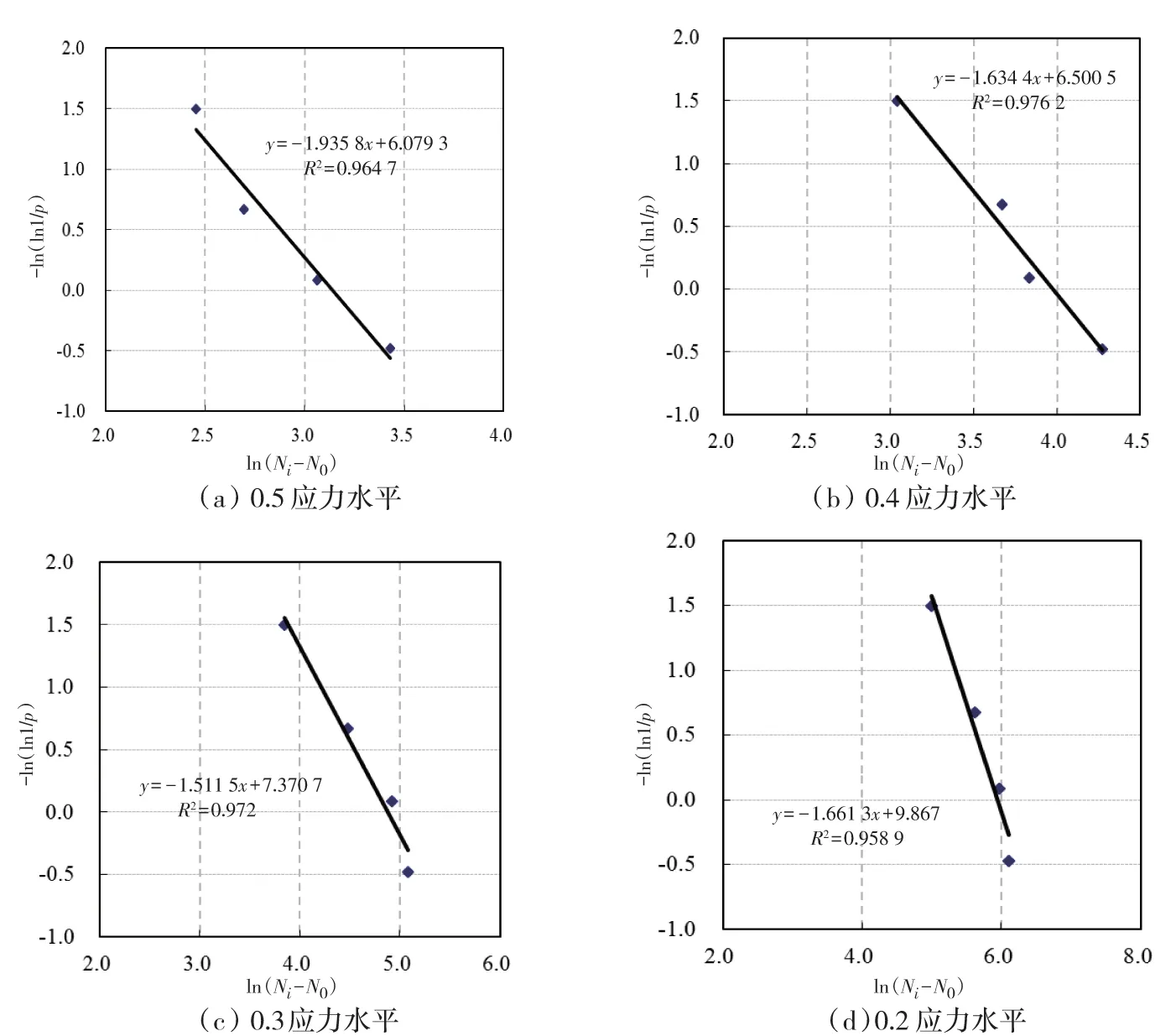
图1 AC-13沥青混凝土寿命分布特征参数相关性Fig.1 The correlation of characteristic parameters of fatigue life distribution function for AC-13 mixture

由图1、图2可以看出：-ln(ln1/p)和lg(Ni-N0)呈现显著的线性相关。Weibull分布函数能较为清晰地反映出沥青混凝土材料的寿命概率分布。并在相应试验条件下可由此对一定保证率下的材料疲劳失效寿命进行预估。

根据不同试验条件下的材料失效寿命分布函数，可以获取相应的寿命估计量，并根据不同可靠度设计需求选择不同保证率下的材料疲劳寿命分布，绘制出其疲劳曲线以及疲劳方程。见图3为50%保证率下的3种沥青混凝土材料疲劳寿命曲线。

通过试验结果分析，三参数WEIBULL分布参数拟合优度不仅高于两参数，而且根据图4单一试验条件下的材料失效率函数曲线比较可以看出[10]：由于考虑了最小特征寿命，材料失效率从最小特征寿命开始逐渐增大，避免了两参数曲线在早期阶段的不合理的失效估计。

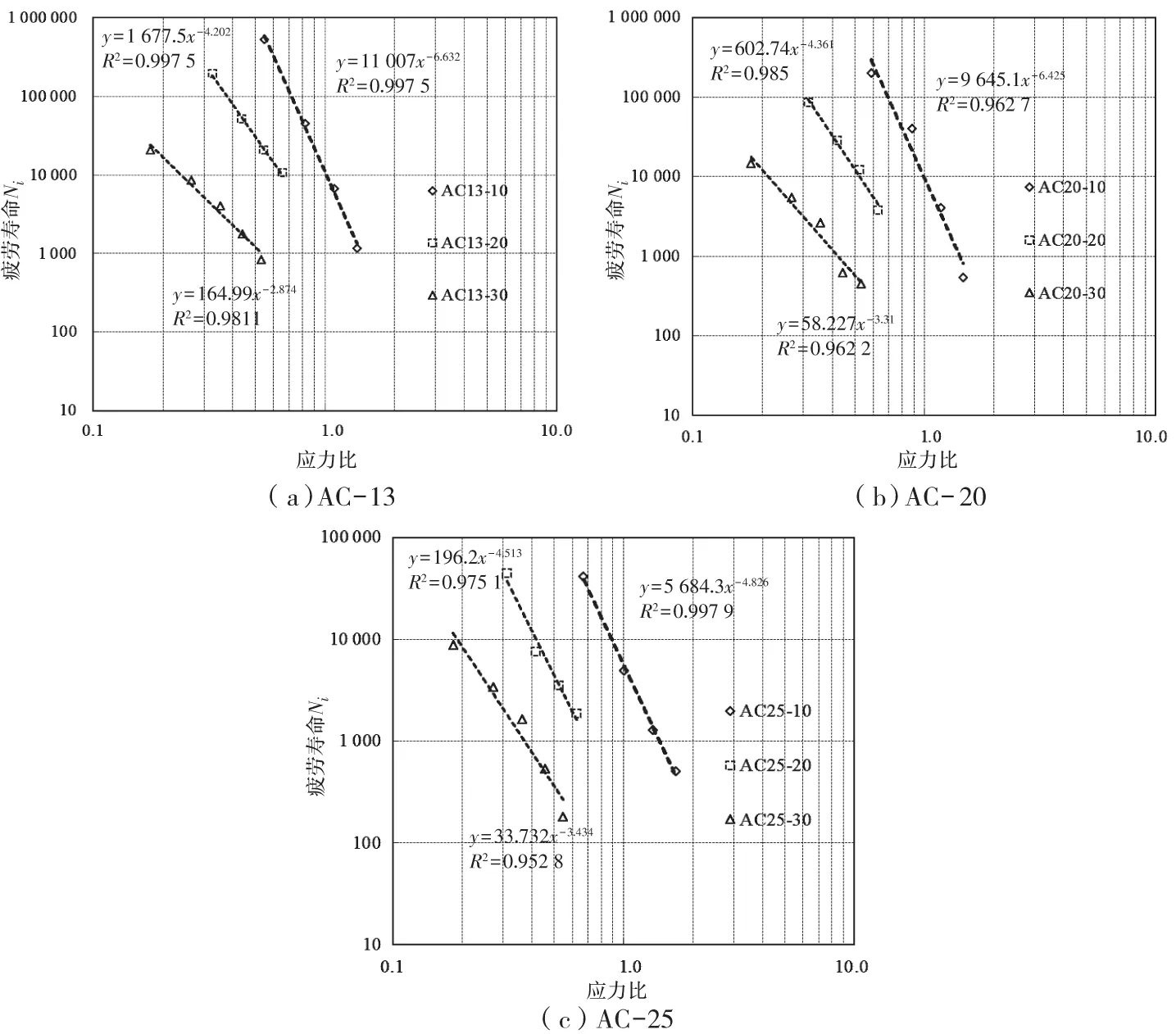
图3 3种沥青混凝土材料50%保证率下疲劳曲线Fig.3 Fatigue curve of three asphalt concretes of 50% reliability

图4 AC-13沥青混凝土材料失效率函数曲线(20 ℃，0.4应力比)Fig.4 Failure rate curve of asphalt concretes(20 ℃，0.4 stress rate)

3 结 论

笔者通过间接拉伸疲劳试验分析了3种不同沥青混凝土材料疲劳失效特性。采用考虑三参数的Weibull分布函数对不同加载条件下材料疲劳寿命分布特征进行模拟，提出了基于位置参数迭代计算下的特征参数估算方法。计算结果显示：考虑初始尺度参数和形状参数的迭代计算方法能较好地估计出满足一定精度要求的位置参数N0；利用试验结果获得的表征Weibull分布特征函数能较为清晰地反映出不同沥青混凝土材料的寿命概率分布，并给出了50%保证率下的材料疲劳寿命曲线和疲劳方程，为后续沥青路面使用性能分析提供了基础数据。

[1] 贾侃.半刚性基层材料的疲劳特性研究[D].西安：长安大学，2008. JIA Kan.StudyontheFatiguePerformanceofSemi-rigidBaseCourseMaterials[D].Xi’an: Chang’an University, 2008.

[2] 熊华锋.复合材料疲劳分散性与强度分散性的关系[D].南京：南京航空航天大学，2009. XIONG Huafeng.ARelationshipofDispersitybetweenFatigueLifeandStrengthofComposites[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.

[3] 李詠侠，刘再锋，郑峰，等.基于Weibull分布的冲压模具用硬质合金耐冲击疲劳性能研究[J].稀有金属与硬质合金，2012，40(4)：50-55. LI Yongxia, LIU Zaifeng, ZHENG Feng, et al. Research on impact fatigue performance of stamping die cemented carbides based on Weibull distribution[J].RareMetalsandCementedCarbides, 2012，40(4)：50-55.

[4] 赵造东.水工混凝土受压疲劳性能及累积损伤研究[D].昆明：昆明理工大学，2011.

ZHAO Zaodong.StudiesontheFatiguePropertyandCumulativeDamageofHydraulicConcreteundertheCompressiveFatigueLoad[D]. Kunming: Kunming University of Science and Technology, 2011.

[5] 董玲云，何兆益，黄刚，等.热再生沥青混合料的疲劳特性研究[J].重庆交通大学学报(自然科学版)，2013，32(4)：606-609. DONG Lingyun, HE Zhaoyi, HUANG Gang, et al. Research on fatigue properties of reclaimed asphalt pavement[J].JournalofChongqingJiaotongUniversity(NatureScience), 2013，32(4)：606-609.

[6] 黎晓，梁乃兴.应力控制模式下沥青混合料劈裂疲劳试验研究[J].中外公路，2013，33(5)：276-279. LI Xiao, LIANG Naixing. Research on the indirect tensile test of asphalt concrete in stress control[J].JournalofChina&ForeignHighway, 2013，33(5)：276-279.

[7] 黎晓，梁乃兴.间接拉伸试验条件下沥青混合料的疲劳行为[J].重庆交通大学学报(自然科学版)，2013，32(6)：1162-1165. LI Xiao, LIANG Naixing. Fatigue performance of asphalt mixes in indirect tensile test[J].JournalofChongqingJiaotongUniversity(NatureScience), 2013，32(6)：1162-1165.

[8] 高智杰，梁乃兴，肖雄.水对沥青混合料疲劳寿命影响的试验研究[J].重庆交通大学学报(自然科学版)，2010，29(2)：199-202. GAO Zhijie, LIANG Naixing, XIAO Xiong. Test study on water affection on the fatigue performance of asphalt pavement[J].JournalofChongqingJiaotongUniversity(NatureScience), 2010，29(2)：199-202.

[9] 吴旷怀，凌宏杰.大样本条件下沥青混合料疲劳试验参数的概率分布分析[J].广州大学学报(自然科学版)，2007，6(3)：72-76. WU Kuanghuai, LING Hongjie. Probability distribution analysis of fatigue test results for asphalt mixture with a large sample[J].JournalofGuangzhouUniversity(NatureScienceEdition), 2007，6(3)：72-76.

[10] 黄明.环氧沥青混合料的疲劳行为研究[J].重庆交通大学学报(自然科学版)，2016，35(1)：46-50. HUANG Ming. Research on fatigue behavior of epoxy asphalt mixture[J].JournalofChongqingJiaotongUniversity(NatureScience), 2016，35(1)：46-50.

[11] 孙杰.基于应力控制模式下的沥青混合料疲劳开裂预估模型的研究[D].广州：华南理工大学，2010. SUN Jie.ResearchonFatigueCrackingPredictionModelofAsphaltMixtureBasedonStressControlModel[D]. Guangzhou: South China University of Technology, 2010.

[12] 沙爱民，贾侃，李小刚.半刚性基层材料的疲劳特性[J].交通运输工程学报，2009，9(3)：29-33. SHA Aimin, JIA Kan, LI Xiaogang. Fatigue performance of semi-rigid base course materials[J].JournalofTrafficandTransportationEngineering, 2009，9(3)：29-33.

[13] 高镇同.疲劳应用统计学[M].北京：国防工业出版社，1986. GAO Zhentong.StatisticsinFatigue[M]. Beijing: National Defense Industry Press, 1986.

(责任编辑 刘 韬)

Estimation of Fatigue Failure of Asphalt Concrete Based on Three-Parameter Weibull Distribution

LI Xiao1，2，LIANG Naixing2，CHENG Zhihao1

(1. National Engineering Laboratory for Surface Transportation Weather Impacts Prevention,Broadvision Engineering Consultants, Kunming 650041, Yunnan, P.R.China;2. School of Civil Engineering, Chongqing Jiaotong University，Chongqing 400074，P.R.China)

Weibull distribution is widely used in asphalt mixes fatigue failure fitting. Compared with two-parameter Weibull distribution, three-parameter Weibull distribution shows better practicability in the situation that fatigue failure does not exist at initial steps. Through indirect tension test (IDT) at different stress levels and different temperatures, the fatigue behavior of three different asphalt concrete were analyzed with location parameter using iterative computations of scale parameter, shape parameter. Combined with test data, the distribution function was calculated based on three characteristic parameters. The results show more reasonable fitting accuracy of three-parameter Weibull distribution than its calculated results by others methods. The fatigue curves and fatigue equations at different test conditions of 50% reliability are obtained.

road engineering; asphalt concrete; stress control; three-parameter Weibull distribution; estimation of fatigue failure

10.3969/j.issn.1674-0696.2017.01.07

2015-09-21；

2015-11-19

云南省交通运输厅科技项目基金[云交科教2014[231]-(二)]；云南省科技创新强省国际科技合作专项基金(2009AC0009)

黎 晓(1982—)，男，重庆人，工程师，博士，主要从事沥青路面结构分析和道路建材方面的研究。E-mail: prettylousy@163.com。

U416.217

A

1674-0696(2017)01-036-06