基于Navier-Stokes方程的干涉相位图处理

王紫秀 岳 军 黄 攀

(1.青岛理工大学 青岛 266000)(2.海军工程大学 武汉 430033)

基于Navier-Stokes方程的干涉相位图处理

王紫秀1岳 军1黄 攀2

(1.青岛理工大学 青岛 266000)(2.海军工程大学 武汉 430033)

干涉合成孔径声纳(INSAS)形成的干涉图中,条纹代表着地形高度信息。要对干涉相位图中由系统和环境引起的很多散斑噪声进行滤波,同时,保留边缘形成的结构和不连续性。文章考虑用一个新的偏微分方程(PDE)模型去对基于Perona-Malik(P-M)方程和流体力学中的Navier-Stokes(N-S)方程的干涉图进行滤波。实验结果表明,该方法能够有效地对相位图像进行去噪并且可以保护图像边缘结构。

干涉相位图; PDE; 滤波; N-S方程; INSAS

Class Number TP391

1 引言

为了获得地形测量,干涉合成孔径声纳(INSAS)[1]形成的干涉图受到越来越多的关注。在实际测量的过程中,由干涉图得到的相位图总是由于地形起伏、采样和水下环境有许多斑纹噪声。相位条纹包含着信息去估计地形高度。现在的困难来自于高水平的散斑噪声,在重建过程中将引入一些错误。所以,对早期的干涉相位图像进行滤波是关键点所在。

图1 实验获得的噪声图

图2 仿真获得的噪声图

在过去的几年里,很多过滤器应用在这方面的图像中,比如:均值滤波、中值滤波、高斯滤波等。但是,这些方法不适应于当地噪声水平的变化,也不能保护边缘的稳定。最近的研究表明,PDE理论为图像处理提供了基础[2～5]。基于PDE图像滤波方法考虑了噪声图像的特点,和传统的算法相比有着更多的特点和性能。现在已经发现,PDE方法可以更有效地对图像进行去噪,并且很好地保护边缘[6～7]。

在过去的几十年内,PDE方法[8～9]应用到图像去噪方面发展迅速并且应用广泛,它可以很好地对图像进行去噪并且更好地保护边缘。而且,耦合的PDE方法[10～12]也逐渐开始研究起来,它用来解决解决单一方程不能处理的问题。在1990年,Perona-Malik[13]提出下面的非线性扩散模型,在这一领域有很大的影响。

N-S方程是经典流体力学方程[14],可被视为对流扩散过程。M. Bertalmio, A. L. Bertozzi and G. Sapiro提出了可以将N-S方程应用到图像和视频的修复[15～16]。主要思想就是把图像强度看作是流函数的二维不可压缩流。本文在navier - stokes流体动力学的基础上提出了一个新的PDE方法对图像进行滤波,这个方法有成熟的理论和数值结果的直接优势。

2 基于N-S方程的图像处理模型

PDE方法在图像滤波方面是源于热扩散现象,包括各向同性和各向异性扩散。近年来,对流项引入了扩散方程,2001年,M.Bertalmio等提出了一个使用N-S流体动力学中的流函数对图像和视频进行修复的方法。这个想法是把图像强度看作是流函数的二维不可压缩流,不可压缩流服从N-S方程:

利用这个事实,用一个图像矩阵I替换Ψ,那么二维不可压缩流和输入图像的对比如图所示。

表1 二维不可压缩流和输入图像的对比

在图像处理方面,现在有对比后的涡度-流函数公式:

其中ω是涡度,γ代表流体粘度。这是一个流体动力学领域的对流扩散方程。

图像修复方法其实是根据边缘的数据恢复内部的数据。正因如此,这是一个边界问题。然而,这是一个对图像滤波初始边界问题。基于涡度方程,本文引入了一个新的对流项,提出了一种新的去噪模型:

3 数值实验结果和分析

这个方法将很好地帮助PDE方程得到精确数值解。一般来说,主要有两种方法来获得近似解,一个是标准的有限差分方法,另一个是有限元法。

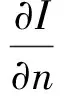
图3 数值结果

很明显可以看出:新模型可以更好地对图像进行去噪,并且能更好地对边缘进行保护。下面将对实验中获得的图像进行处理,结果如下。

图4 图像处理结果图

通过比较可以看出:新模型保留了图像边缘细节而有效地去除噪声。接下来,为了可以定量比较,在图像处理过程中利用了三个常用的误差度量:等效视数(ENL),边缘保持指数(EPI)和残余点。

表2 两个模型的三个误差度量对比

这个表格很明显地对比了P-M模型和新模型的三个参数,可以看出,新模型有更高的ENL和EPI,以及更少的残余点。因此,新模型一般表现良好和更好地保持图像边缘细节。

4 结语

本文基于N-S不可压缩流提出了一种新的PDE模型用于对早期干涉图进行滤波。该模型引入了对流项解决边界漂移现象。数值实验结果和分析表明,该方法能够有效地去除噪声,更好地保持图像边缘细节。

[1] Caroline Lacombe, Gill Aubert. Filtering Interferometric Phase Images By Anisotropic Diffusion [J]. Image Processing ICIP, 2003,2(3):141-144.

[2] Leonid I. Rudin, Stanley Osher, Emad Fatemi. Nonlinear total variation based noise removal algorithms [J]. Physica D:Nonliear Phenomena, 1992,261-268.

[3] Chen Tang, Fang Zhang, Zhangqing Chen. Contrast enhancement for electronic speckle pattern interferometry fringes by the differential equation enhancement method [J]. Applied Optics, 2006,10(45):2287-2294.

[4] Y.-D.Wu, Y.Sun, H.-Y.Zhang, S.-X.Sun. Variational PDE based image restoration using neural network [J]. IET Image Process, 2007,1(1):85-93.

[5] Y.Chen, C.A.Z.Barcelos, B.A.Mair. Smoothing and Edge Detection by Time-Varying Coupled Nonlinear Diffusion Equations [J]. Computer Vision and Image Understanding, 2001,82(2):85-100.

[6] Weickert J. Application of nonlinear diffusion in image processing and computer vision[J]. Acta Math, 2001,1(LXX):33-50.

[7] Luo H G, Zhu L M, Ding H. Coupled anisotropic diffusion for image selective smoothing [J]. Signal Processing, 2006,86:1728-1736.

[8] Pan Huang, Jun Yue, Maolin Wang. Coupled Partial Differential Equations Method for InSAS Interferogram Filtering[J]. Applied Mechanics and Materials, 2012,487:103-106.

[9] P.Perona, J.Malik. Scale-Space and Edge Detection Using Anisotropic Diffusion [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(7):21-24.

[10] M.Bertalmio, A.l.Bertozzi, G.Sapiro. Navier-Stokes Fluid Dynamics and Image and Video Inpainting [J]. Computer Vision and Pattern Recognition, 2001,1:355-362.

[11] Witkin A P. Scale-Space filtering[J]. In Processing of IJCAI, Karlsruhe,1983:1019-1021.

[12] Sylvie Teboul, Gilles Aubert, Michel Barlaud. Variational Approach for Edge-Processing Regularization Using Coupled PDE’s [J]. IEEE Transactions on image processing,1998,7(3):387-397.

Filtering Interferometric Phase Image Based on Navier-Stokes Equation

WANG Zixiu1YUE Jun1HUANG Pan2

(1. Qingdao Technological University, Qingdao 266000) (2. Naval University of Engineering, Wuhan 430033)

Interferogram from the Interferometric Synthetic Aperture Sonar(INSAS) has fringes representing the terrain height information. The interferometric phase images with much speckle noise caused by the system and environment are filtered, at the same time the structures and discontinuities formed by the fringes are preserved. In this paper, a new partial differential equation(PDE) method is considered to filter the phase images based on the Perona-Malik(P-M) equation and Navier-Stokes(N-S) equations for fluid dynamics. Experimental results indicate that this method is able to de-noise the phase images and preserve the image fringes structure effectively.

interferometric phase image, PDE, filtering, N-S equation, INSAS

2016年7月7日,

2016年8月25日

国家自然科学基金项目课题“多物理场图像处理与应用(编号:61271015)”资助。

王紫秀,女,硕士,研究方向:偏微分方程的图像处理中的应用。岳军,男,博士,副教授,研究方向:偏微分方程在海洋中的应用。黄攀,男,博士,研究方向:干涉合成孔径图像处理。

TP391

10.3969/j.issn.1672-9730.2017.01.020