EFP战斗部结构参数优化设计研究

李 剑

(安徽神剑科技股份有限公司，合肥 230022)

【装备理论与装备技术】

EFP战斗部结构参数优化设计研究

李 剑

(安徽神剑科技股份有限公司，合肥 230022)

基于研究EFP穿甲威力目的，利用LS-DYNA软件对球缺型EFP成形进行数值模拟研究；分析了曲率半径、药型罩壁厚、壳体厚度等参数对EFP成形性能的影响规律；优化得到了药柱高度50 mm、装药直径40 mm的EFP战斗部结构方案；研究结论将为EFP优化设计提供参考依据。

EFP；结构参数；药型罩；数值模拟；优化设计

EFP即爆炸成型弹丸，是利用聚能装药原理，通过炸药的聚能爆轰作用，使金属药型罩压垮变形而成形出一个具有较高质心速度和一定结构形状的弹丸，从而可以以动能侵彻目标。随着装甲目标防护能力的不断增强，需要设计速度更高、动能更大的高威力EFP，以满足侵彻性能要求[1-2]。

影响EFP成形性能的关键因素有装药性能、装药结构、药型罩材料和结构参数等[3]。而装药结构是EFP战斗部优化设计中的关键部件。本文以球缺形药型罩形成EFP为例进行研究，采用数值模拟方法分别模拟不同R1、h以及δ方案下EFP成形过程，分析药型罩曲率半径、药型罩壁厚、壳体厚度等参数对EFP成形性能的影响规律，最终找出EFP战斗部结构参数最佳组合方案。

1 模型建立及方案确定

1.1 模型建立

计算模型采用如图1所示的典型球缺罩EFP战斗部装药， 其中装药为8701炸药，药型罩材料为紫铜，壳体材料为钢[4]。图1中各参数的物理意义如下：α为切向半锥角；R1为药型罩内曲率半径；R2为药型罩外曲率半径；δ为壳体厚度；L为装药高度；DK为装药直径；药型罩壁厚h=R2-R1[5]。

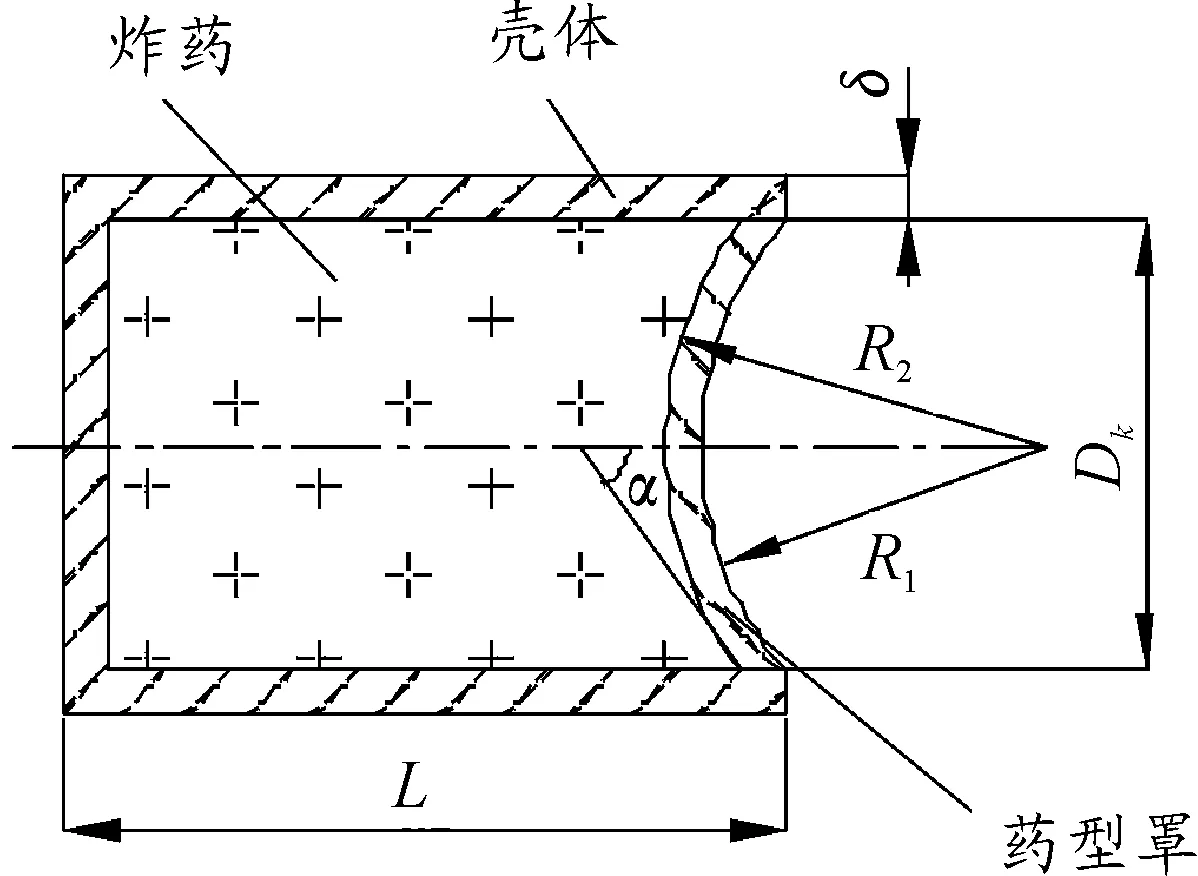
图1 EFP战斗部结构

采用动力分析有限元程序LS-DYNA进行EFP数值模拟，并采用拉格朗日算法[6-7]。

1.2 方案确定

数值模拟计算共计21种方案，具体步骤：在战斗部其他结构参数确定前提下，依次针对7种不同R1、h、δ的EFP进行成形模拟计算[8]，分析3种参数对EFP成形性能的影响规律，分别找出R1、h、δ的与装药直径DK的最佳配比关系，最终确定EFP战斗部结构参数最佳组合方案[9-10]。

2 曲率半径方案计算分析

2.1 曲率半径方案确定

在EFP战斗部其他结构参数确定前提下，针对7种不同R1的EFP进行成形模拟计算，计算方案如表1所示。

表1 R1计算方案 mm

2.2 曲率半径方案计算分析

计算不同R1方案下，成形EFP的v、E以及l/d结果对比见表2、图2。

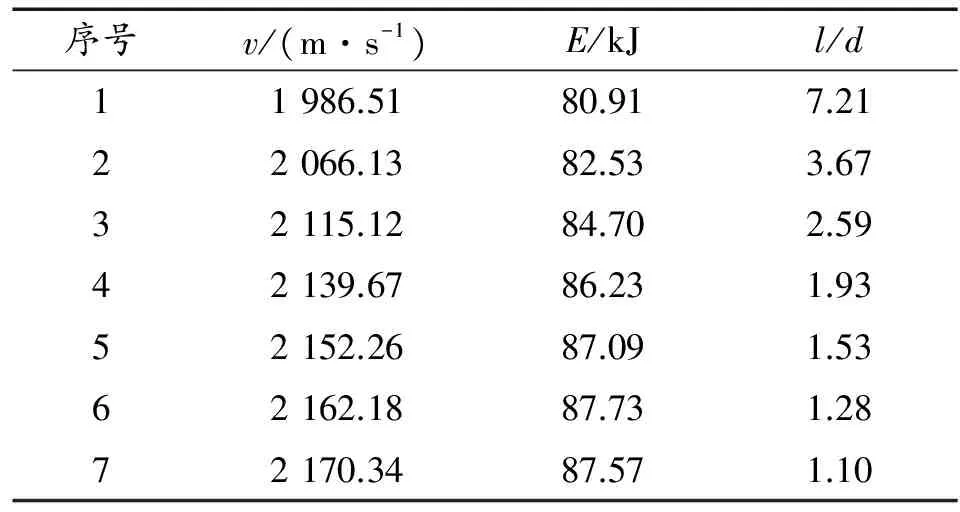
表2 不同R1方案下的v、E、l/d

图2 v、l/d与R1关系

从表2、图2可以得出，v随着R1的增大也随之增大。但是增长幅度随R1增大而逐渐减小。当R1≥45 mm，v增幅不大，R1对速度影响减弱。

l/d随着R1增大而减小。l/d较大时，EFP头、尾部速度差较大，容易出现拉伸断裂；l/d较小时，EFP内部容易出现空腔，影响穿甲能力。

E随着R1的增加先增长后减小，说明R1较大时候，容易出现碎裂现象，导致EFP品质下降，降低侵彻性能。

不同R1方案模拟计算，EFP在60 μs形状对比如图3所示。

图3 不同R1的EFP外形(t=60 μs)

图3可以得出：R1对 EFP的质心位置有较为明显的影响。随着R1的增大，EFP质心向其头部靠近。EFP长度逐渐减小，而且R1越大，形成的EFP空腔体积越大。这将造成弹丸穿甲能力下降。R1较小时，EFP的稳定裙部分较小，整体细长，影响EFP的飞行稳定性。

综合分析得出，R1=1～1.125DK时，所形成的EFP具有较高的飞行稳定性以及较大的穿甲威力。

3 药型罩壁厚方案计算分析

3.1 药型罩壁厚方案确定

本节确定R1=DK前提下，针对7种不同h的EFP进行成形模拟计算，计算方案见表3。

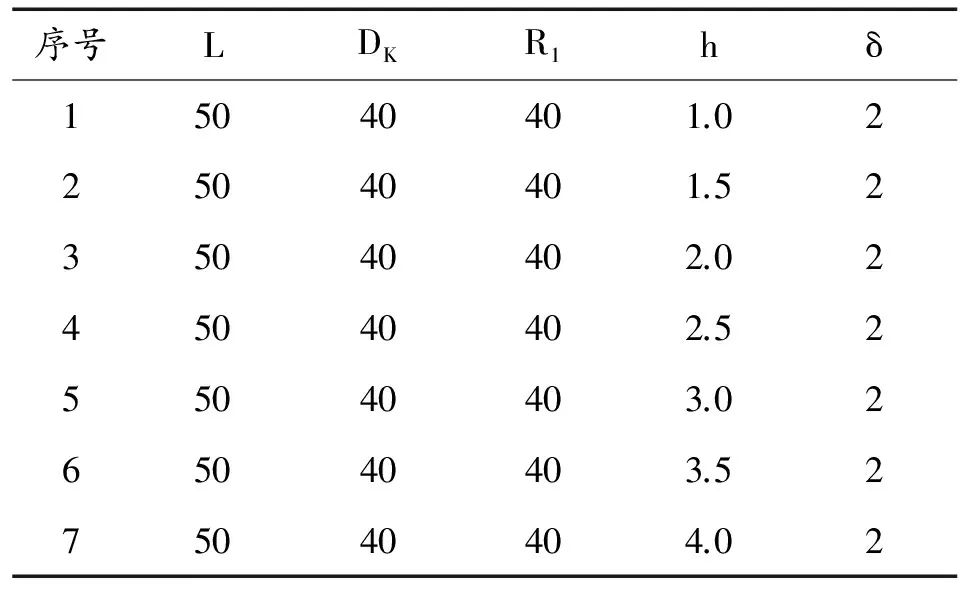
表3 h计算方案 mm

3.2 药型罩壁厚方案计算分析

计算不同h方案下，成形EFP的v、E以及l/d结果对比见表4、图4。

表4 不同h方案下的v、E、l/d

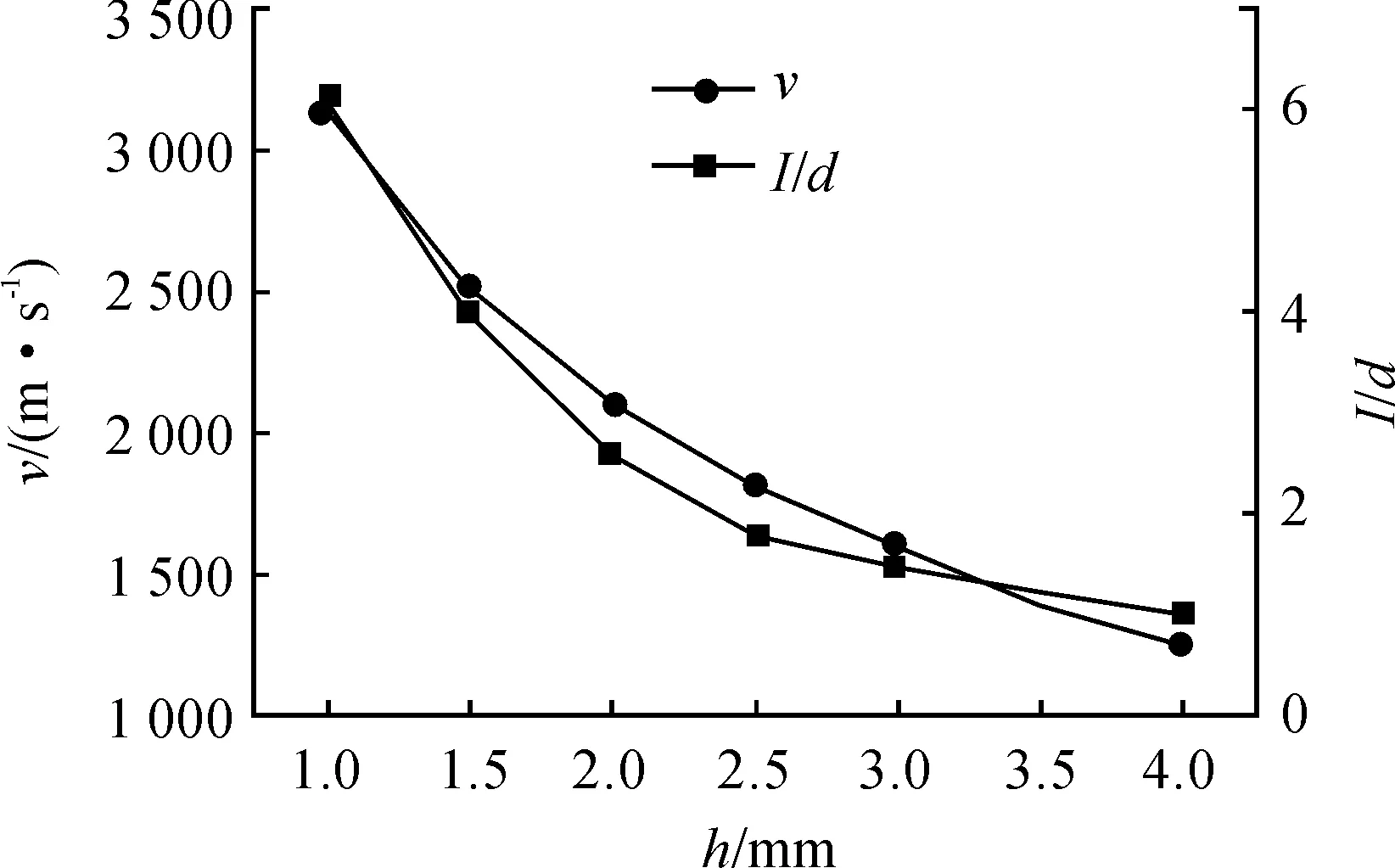
图4 v、l/d与h关系

由表4、图4可以得出，v、E以及l/d与h成反比例关系，随着h增大，v、E、l/d均减小。l/d过大，EFP容易出现拉伸断裂，l/d过小，容易造成EFP空腔，影响穿甲能力。所以在l/d适中情况下，尽量选择h较小的药型罩。

不同h方案模拟计算，EFP在60 μs形状对比如图5所示。

图5 不同h的EFP外形(t=60 μs)

图5可以得出，h≤1.5 mm，EFP形状细长，拉伸现象严重；h过小时，甚至出现中间断裂，严重影响侵彻性能；h≥3 mm，EFP形状短粗，中间存在较大空腔，不利于穿甲。

综合分析得出，h=0.05～0.0625DK时，所形成的EFP具有较高的飞行速度以及较大的侵彻动能。

4 壳体厚度方案计算分析

4.1 壳体厚度方案确定

在R1=DK、h=0.05DK条件下，针对7种δ的EFP进行成形模拟计算，计算方案见表5。

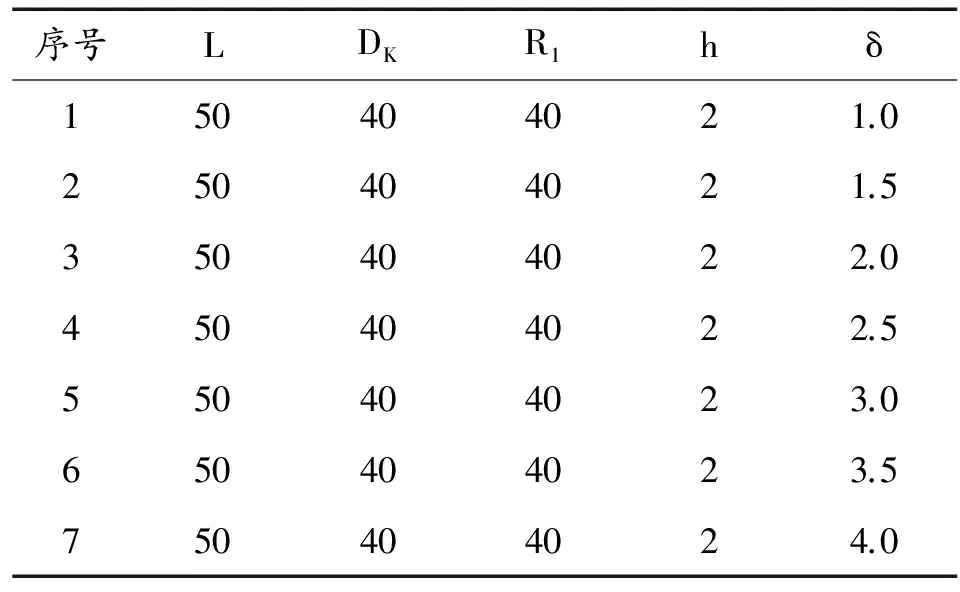
表5 δ计算方案 mm

4.2 壳体厚度方案计算分析

计算不同δ方案下成形EFP的v、E以及l/d结果对比见表6、图6。

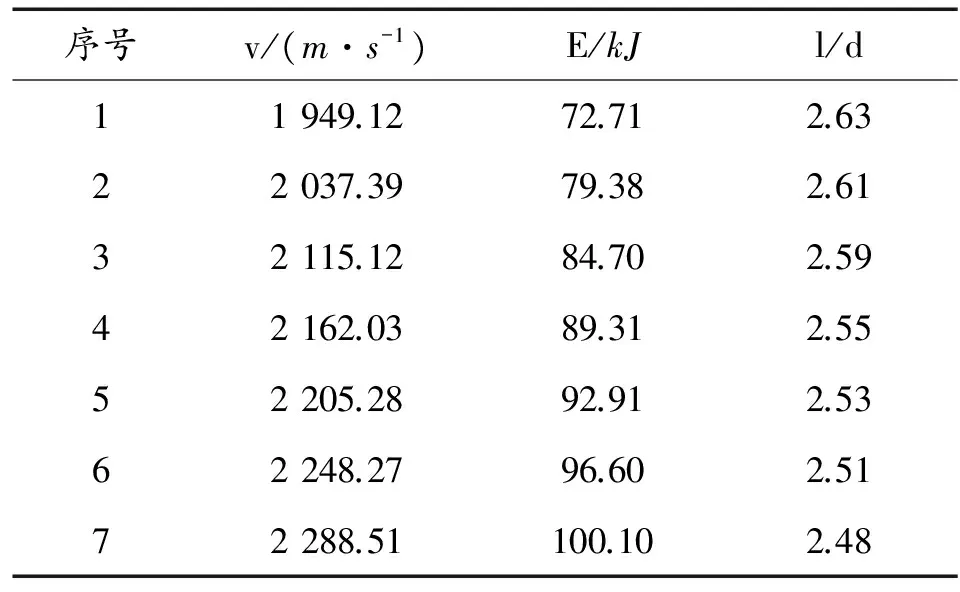
表6 不同δ方案下的v、E、l/d

图6 v、l/d与δ关系

由表6、图6可以得出，随着δ增大，v、E增大；l/d近似成线性关系。减小幅度不大，说明δ对l/d影响不大。

不同δ方案模拟计算，EFP在60 μs形状对比如图7所示。

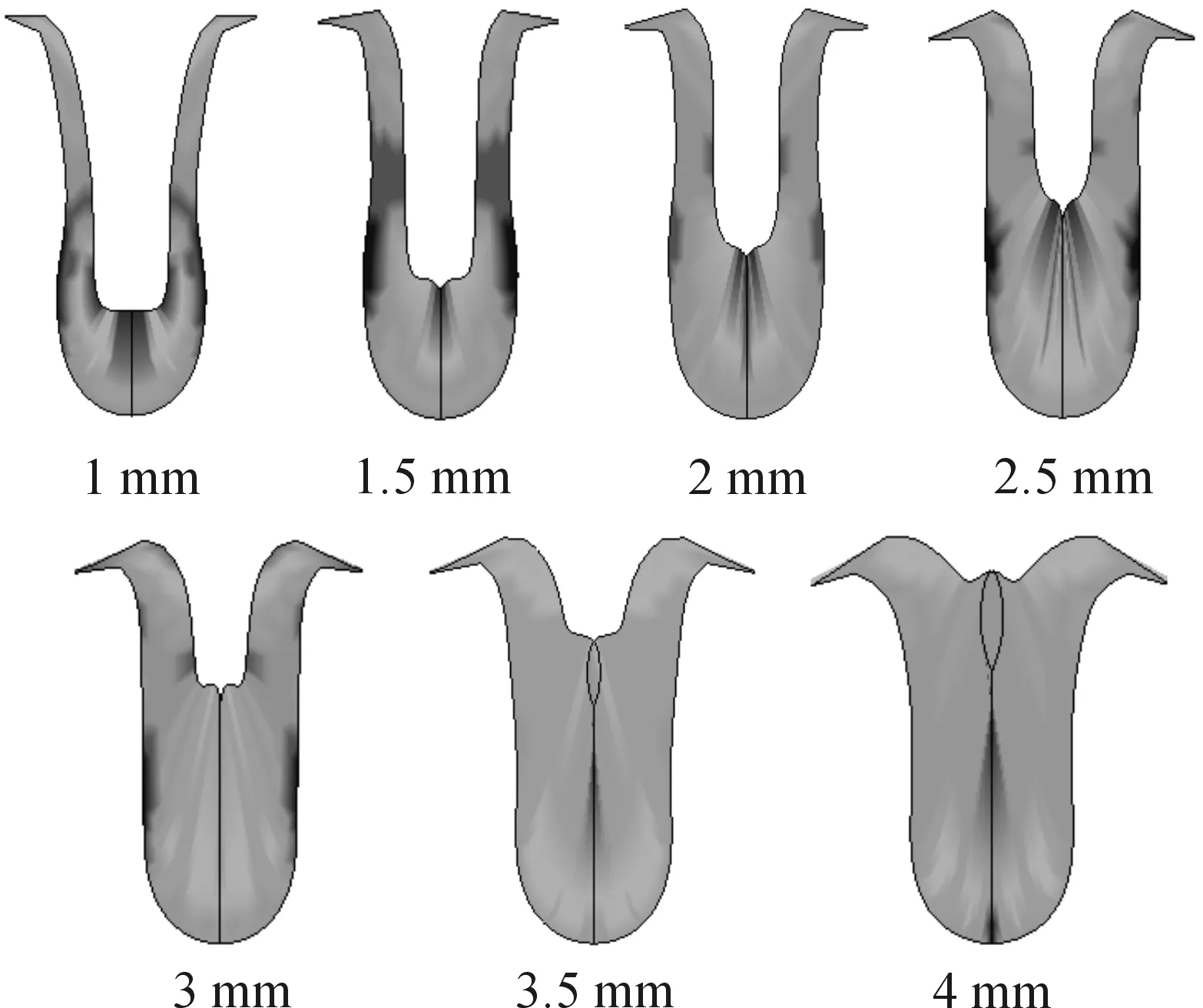
图7 不同δ的EFP外形(t=60 μs)

由图7可以得出，δ增大，药形罩轴向速度增大，从而使EFP从简单的翻转拉伸逐渐过渡到挤压成密实的长杆形状。如果δ过大，就会使EFP重心后移，不利于飞行稳定性；而当δ过小时，形成的EFP存在空腔，虽使重心靠前，有利于EFP的飞行稳定性，但会减小EFP的v、E，不利于穿甲。

综合分析可得，δ=(0.050 0～0.062 5)DK时，所形成的EFP具有较强的飞行稳定性以及较大的侵彻动能。

5 总结

综合考虑得出R1、h及δ与DK的最优综合匹配为R1=1～1.125DK、h=0.05～0.062 5DK、δ=0.05～0.062 5DK，为以后进行EFP优化设计提供了参考依据。

[1] 朱宝祥.大威力EFP战斗部技术研究[D].南京：南京理工大学,2007：1-18.

[2] 黄群涛.环形EFP形成机理研究[D].南京：南京理工大学,2008：1-10.

[3] 卢芳云，李翔宇，林玉亮.战斗部结构与原理[M].北京：科学出版社，2009：66-72.

[4] 尹建平，付璐，王志军，等.药型罩结构参数对EFP成型影响的灰关联分析[J].解放军理工大学学报(自然科学版)，2012，1(3)：101-105.

[5] 蒋建伟，杨军，门建兵，等.结构参数对EFP成型影响的数值模拟[J].北京理工大学学报，2004，11(24)：939-941.

[6] 时党勇，李裕春，张胜民.基于ANSYS/LS-DYNA 8.1进行显式动力分析[M].北京：清华大学出版社，2005：250-263.

[7] LSTC inc.LS-DYNA KEYWORD USER’S MANUAL(Version 970)[M].北京：水利水电出版社，2008.

[8] 顾文彬，刘建青，唐勇，等.球缺型EFP战斗部结构优化设计研究[J].南京理工大学学报(自然科学版)，2008，32(2)：165-170.

[9] 张志春，孙新利，孟会林，等.EFP成型影响因素的数值模拟[J].弹箭与制导学报，2006,26(1)：227-231.

[10]郭支明，王志军，吴国东.EFP战斗部参数优化设计[J].弹箭与制导学报，2005,25(4)：159-161.

(责任编辑周江川)

Structural Parameters Optimization Design of EFP Warhead

LI Jian

(Anhui Shenjian Technology Company Limited, Hefei 230022, China)

Based on the study of EFP penetrating power, numerical simulation of EFP forming by using LS-DYNA software was proposed. The influence rule of R1，h，δ and other parameters on the formability of EFP was analyzed. The optimized structure of EFP warhead withL=50 mm andDk=40 mm was obtained. The conclusion can give a reference for the optimization design of EFP.

EFP; structure parameter; medicine type cover; numerical simulation; optimization design

2016-08-11；

2016-09-17

李剑(1976—)，男，工程师，主要从事弹药工程研究。

10.11809/scbgxb2017.01.009

李剑.EFP战斗部结构参数优化设计研究[J].兵器装备工程学报，2017(1):36-39.

format:LI Jian.Structural Parameters Optimization Design of EFP Warhead[J].Journal of Ordnance Equipment Engineering,2017(1):36-39.

TJ413.+2

A