基于正交函数系最小二乘拟合的姿态平滑方法

刘宏建，蔡中祥，刘子义

(信息工程大学 地理空间信息学院，郑州 450052)

【装备理论与装备技术】

基于正交函数系最小二乘拟合的姿态平滑方法

刘宏建，蔡中祥，刘子义

(信息工程大学 地理空间信息学院，郑州 450052)

针对高速测控目标姿态数据平滑过程中的微小抖动及处理滞后现象，提出了基于正交函数系最小二乘拟合的姿态数据实时平滑方法，该方法具有平滑效果好、实时性强，基本消除了姿态数据的“抖动”现象，对飞行特性不太平稳的目标适应性较强，在无人机试验中得到了良好的应用。

高速测控目标；正交函数系；最小二乘拟合；实时姿态平滑

无人机、直升机、导弹等由地面测控网跟踪、量测、控制的飞行目标称为高速测控目标[1]。有别于常规运动目标，高速测控目标的运动速度快，地面测控网测量获取的目标实时数据帧率高，单个目标帧率可高达20帧/s，这种由地面测控网实时跟踪、测量获得的高速目标实时数据称为高速测控数据[2]。高速测控数据记录了飞行目标的实时状态、位置、方位、姿态、速度、加速度等信息，是分析目标各种性能、指标、参数的基本依据[3]。姿态数据是一类重要的实时测控数据，包括偏航角、侧滚角和俯仰角，总称目标姿态角，是目标相对惯性平台坐标系的转动角[3]。

由于受地面测控设备对目标跟踪精度及灵敏度限制，一般在设备上位机中会对高速测控数据进行平滑滤波处理，但数据平滑滤波往往不能完全消除目标姿态抖动与跳变现象，尤其在地面指控显示系统中进行目标飞行过程监控时，仍需结合GIS动态显示机制对目标姿态数据进行二次平滑[4]。目标姿态数据实时平滑算法必须满足：一是正确性，采用测控设备对目标跟踪的实测数据作为数据源，要求姿态计算结果准确，目标姿态同目标实时轨迹的走向保持一致；二是稳定性，保证目标姿态实时计算结果平稳、连续，不能出现姿态的突然“抖动”现象，即导弹或直升机、无人机在二三维场景飞行过程中，不能突然出现大幅度 “摆头”或“掉头”现象；三是实时性，由于受雷达或光电经纬仪等跟踪设备数据帧率的限制，目标姿态计算及实时平滑处理算法对每帧数据的处理时间必须小于实时数据帧的帧间隔。

1 主流算法及存在问题

目前，基于GIS的高速测控目标姿态数据实时平滑的方法大致可分为两类，第一类是基于角度差阈值修正目标姿态角的平滑方法[5-7]，其原理是利用上游目标姿态角序列的方差与经验常数的乘积作为阈值控制当前姿态角的抖动范围；第二类是加权最小一乘平滑方法[8-10]，即在最小一乘模型基础上通过引入自变量权系数设置方式，采用遗传算法提高算法的收敛速度，以克服异常姿态数据所带来的影响。上述两类算法对于飞行特性比较平稳(即飞行曲线较平滑，抖动现象不多)的目标适应性较好，但对于飞行特性不太稳定的目标，还存在下述两个问题：虽然目标姿态“抖动”幅度下降，但目标姿态“抖动”的频率并没有降低，还在进行微小的、频繁的“抖动”；长时间的连续运行过程中，二三维地图场景中显示的目标实时轨迹相对于实际弹道或飞行曲线有明显的滞后现象。

本文在实验过程中，深入分析了上述两个问题产生的原因：上述方法为了保持目标飞行姿态的连续性，限定了目标姿态角的全局阈值，保证了前后两帧实时数据的姿态角度之差不超过全局阈值。但在进行偏航角修正与平滑时，对当前目标偏航角的修正和对下一数据帧目标偏航角的修正是孤立的；如果目标飞行特性不太平稳，则需要进行频繁的迭代计算，占用大量CPU处理时间，导致地图刷新速度下降，因此产生了目标实时轨迹相对于实际飞行曲线有明显的滞后现象。为解决上述问题，提出并实现了基于正交函数系最小二乘拟合的高速测控目标姿态数据实时平滑方法。

2 基于正交函数系的最小二乘拟合

设φj(x)(j=0,1,2,…,n)是区间[a,b]上的函数，点集(x0,x1,x2,…,xm)⊂[a,b]，权系数ωi>0(i=0,1,2,…,m)，如果

则称φj(x)(j=0,1,2,…,n)是关于点集(x0,x1,x2,…,xm)的带权正交函数系。

若基函数φj(x)(j=0,1,2,…,n)关于点集(x0,x1,x2,…,xm)正交，则最小二乘法方程组的矩阵形式可简化为

从而解得：

因此，可得最小二乘拟合多项式：

用Gram-Schmidt正交化方法求φj(x)：

这里：

由于平滑算法的强实时性要求，一般采用低阶(一阶和二阶)拟合多项式：

φ0(x)=1

φ2(x)=(x-α2)φ1(x)-β1φ0(x)

φ*(x)=a0*φ0(x)+a1*φ1(x)

φ*(x)=a0*φ0(x)+a1*φ1(x)+a2*φ2(x)

3 算法实现与分析

3.1 算法实现

基于正交函数系最小二乘拟合的高速测控目标姿态平滑算法(以偏航角平滑为例)的实现流程如图1所示。

图1 算法实现程序流程

步骤1选取高速目标实时数据帧缓存中的m个数据点形成实测点集数据，点集个数m可作为全局配置参数进行调整，即以m个数据点{P0,P1,P2,…,Pm}作为曲线拟合的数据源；

步骤2在高速目标数据帧缓存中第一次获取m个实测点值后，对m个数据点进行Gram-Schmidt正交最小二乘拟合，求出拟合方程f(x)；

步骤5利用飞行目标当前位置坐标及当前偏航角φm驱动符号(或三维模型)在二三维场景中显示；

步骤6将本次计算的m个数据点的修正值中的前m-1个点以及实时获取的下一帧目标数据作为点集数据，转步骤2进行循环处理。

3.2 应用分析

以某次某型号无人机飞行实时监控应用为例，本文对上述基于正交函数系最小二乘拟合的姿态实时平滑方法进行了验证，分别选取点集个数m=6，m=9，m=12时，处理延时如表1所示。

表1 m取值与单帧处理延时关系

可见，算法可以很好地对飞行目标姿态进行平滑处理，使目标能够在二三维场景连续、平稳的运动，无“抖动”现象，并且m值越大，飞行目标姿态平滑的效果越好。当m=6时，单帧目标实时数据处理延时为6.710 μs，当m=12时，单帧目标实时数据处理延时为11.069 μs，从单帧数据处理延时来看，算法的实时性较强，远小于50 ms(跟踪测控设备的数据帧率)的限制。取m=6，无人机姿态平滑前后对比如图2所示。

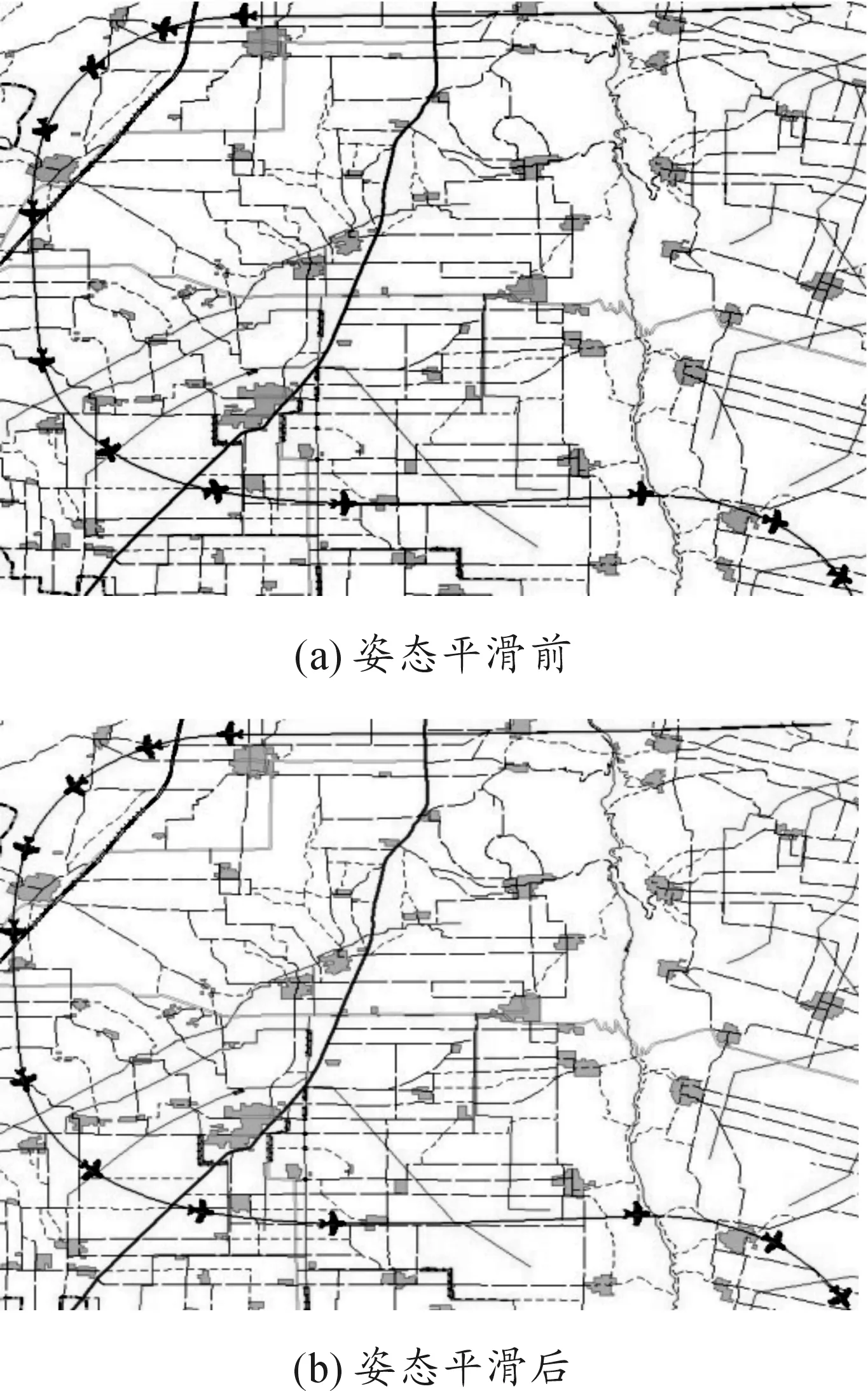
图2 无人机姿态平滑前后对比

4 结论

本文分析了现有高速测控目标姿态数据实时平滑算法存在的主要问题，提出并实现了基于正交函数系最小二乘拟合的高速测控目标姿态平滑方法。该方法基本消除了姿态数据的“抖动”现象，对飞行特性不太平稳的目标适应性较强，在实际应用中取得了良好的效果。

[1] 常显奇，程永生.常规武器装备试验学[M].北京：国防工业出版社，2007.

[2] 刘宏建，刘建忠，蔡中祥.应用“缓存分流”模型的高速测控目标全轨迹显示算法研究[J].测绘科学，2013,38(5):94-96.

[3] 何友金.靶场测控概论[M].济南:山东大学出版社，2009.

[4] 王丽娜.基于GIS的飞行器定位中的匹配方法[J].空间控制技术与应用，2011,37(1):33-35.

[5] 吴文江，陈其工，高文根.基于 PSO 优化参数的最小二乘支持向量机短期负荷预测[J].重庆理工大学学报(自然科学)，2016(3)：112 - 115.

[6] 刘宏建.常规武器装备靶场试验地理空间分析与应用建模研究[D].郑州：信息工程大学，2008.

[7] 王东霞，石恒，贾英宏.航天器姿态指向跟踪的一种自适应滑模控制方法[J].空间控制技术与应用，2010,36(6):22-26.

[8] KOENIG S,LIKHACHEV M.Improved Fast Replanning for Robot Navigation in Unknown Terrain[C]//Proceeding of the 2012 IEEE international Conference on Robotics & Automation,Washington,DC,USA.USA:IEEE,2012:968-975.

[9] 徐小辉，郭小红.外弹道加权最小一乘模型研究与应用[J].飞行器测控学报，2008,27(2):85-88.

[10]FERGUSON D,STENTZ A.The Field D*Algorithm for Improv Fed Path Planning and Replanning in Uniform and Non-uniform Cost Environments [R].Technical Report CMU-RI-TR-05-19.USA:Carnegie Melton School of Computer Science,2005.

(责任编辑周江川)

Attitude Smoothing Method Based on Least Square Fitting of Orthogonal Function System

LIU Hong-jian, CAI Zhong-xiang, LIU Zi-yi

(Institute of Geospatial Information, PLA Information Engineering University, Zhengzhou 450052, China)

Aiming at the small jitter and delay processing phenomenon in high speed measurement and control target attitude data smoothing, we put forward a real-time attitude data smoothing method based on least square fitting of orthogonal function system. The method has good effect and real-time performance, basically eliminates the “chattering” phenomenon of attitude data, and gets a good application in UAV test.

high-speed measurement and control target; orthogonal function system; least squares; real time attitude data smoothing

2016-08-15；

2016-09-20

国家自然科学基金项目(41301125)

刘宏建(1980—)，男，博士，讲师，主要从事军事地理学与作战环境分析方法研究。

10.11809/scbgxb2017.01.005

刘宏建，蔡中祥，刘子义.基于正交函数系最小二乘拟合的姿态平滑方法[J].兵器装备工程学报，2017(1):21-23.

format:LIU Hong-jian, CAI Zhong-xiang, LIU Zi-yi.Attitude Smoothing Method Based on Least Square Fitting of Orthogonal Function System[J].Journal of Ordnance Equipment Engineering,2017(1):21-23.

P231

A