电站锅炉管阵列内声传播特性及时延值测量
安连锁,冯 强,沈国清,姜根山,张世平,王 鹏,张海宇
(1.华北电力大学 能源动力与机械工程学院,电站设备状态监测与控制教育部重点实验室,北京 102206;2.中国城市建设研究院有限公司,北京 100120)
电站锅炉管阵列内声传播特性及时延值测量
安连锁1,冯 强1,沈国清1,姜根山1,张世平1,王 鹏1,张海宇2
(1.华北电力大学 能源动力与机械工程学院,电站设备状态监测与控制教育部重点实验室,北京 102206;2.中国城市建设研究院有限公司,北京 100120)
对电站锅炉管阵列内声传播特性及时延值进行研究,利用Fluent软件对非均匀温度场与均匀温度场、不同管排数及不同布置方式的管阵列内声传播特性进行对比,并搭建管阵列实验台,引入快速集合经验模态分解(EEMD)算法对管阵列内时延值进行测量.结果表明:管阵列内声传播存在声阻带,且在非均匀温度场集合经验模态分解下声阻带向低频段移动,管排数越多,声阻带效应越明显,管道间节距对错列与顺列布置方式下的声阻带有一定影响;基于快速EEMD处理,选用低频段声信号能够获得有效时延值.
电站锅炉;管阵列;声传播特性;时延值;快速集合经验模态分解
现有的电站锅炉定位技术均建立在炉膛内无障碍物环境的基础上,而对管阵列的定位鲜见研究.定位算法的核心部分是时延值测量的准确性,若时延值测量误差较大,则无法得到泄漏点的精确定位.在时延值测量过程中,首先要对管阵列内的声波传播(以下简称管阵列声传播)特性进行研究,笔者对以下2个部分进行了研究:第一部分为水平烟道及尾部烟道内管阵列声传播特性研究;第二部分为管阵列内时延值测量.
1 管阵列声传播特性研究
管阵列声传播特性研究采用数值模拟方法,并结合平面波展开法[1]进行理论验证.
1.1 平面波展开法
声子晶体的二维平面波展开法声波波动方程可表示为
(1)
(2)

u可表示为u=uxi+uyj.式(1)为Z模态,与横向振动相对应;式(2)为XY模态,与纵横耦合振动相对应.
对于气相为基相的传播模型,不存在横波传播,即C44=0,那么声波波动方程可简化为
(3)
将标量Ψ(r,t)引入式(3),那么位移矢量可表示为
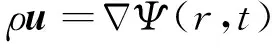
(4)
则存在以下关系式:
(5)
采用随时间变化的波函数来表示Ψ(r,t),即将Ψ(r,t)=exp(-iωt)Ψ(r)带入式(5),并对时间项进行分离,可得
(6)
式中:ω为频率.
由式(6)可知,声波波动方程求解可转化为本征值求解的问题.构成声子晶体的材料属性可通过Bloch原理固体理论和晶格傅里叶展开法在倒格子空间进行展开,从而获得傅里叶级数形式:
(7)
(8)
式中:G为二维晶格倒格矢,用倒格子空间基矢量的方式可表示为G=n1b1+n2b2,b1和b2为倒格子空间基矢量,n1和n2为整数项.
上式中的傅里叶系数为
∬Acd2rT(r)e-iG·r
(9)
式中:S(G)为由Ac、Ci(r)或ρ(r)共同构成的一个周期结构所占面积;Ac为晶格面积;∬Acd2r为对原胞的积分.
根据G是否为0,S(G)可表示为如下形式:
(10)
式中:A1为散射体在二维空间中所占面积;f为声子晶体填充比,f=A1/Ac;ρA为钢柱的密度;ρB为空气的密度.
1.2 均匀温度场下管阵列声传播特性
电站锅炉管阵列一般由多排蛇形管以及起始端和末端的进出口连箱构成,其壁厚为5~10 mm,外径通常为38~57 mm,然而有些锅炉也会采用外径为60 mm或63 mm的蛇形管[2].
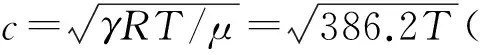
由图2可知,该条件下管排间声传播不存在完全禁带[3],仅在Γ-X方向出现方向性禁带,即不完全禁带,对于10 000Hz以下频段,不完全禁带为2 484~3 687Hz和6 673~7 038Hz.对于气/固型声子晶体,第一带隙中心频率存在关系式Δfmid=c/2a,代入当地声速和晶格常数可得出第一带隙中心频率为3 218.9Hz,与平面波展开法计算结果(3 085Hz)接近,两者误差为4.1%,符合工程误差精度要求.对比图2与图3可知,平面波展开法计算结果与数值模拟结果较为吻合,说明所采用的数值模拟方法是可行的,具有一定的参考价值.

图1 模型边界条件

图2 平面波展开法计算结果

图3 数值模拟结果
1.3 烟气与管道换热对管阵列声传播特性的影响
1.3.1 非均匀温度场建模
烟气流过管排进行换热时不能用简单的数学模型来描述非均匀温度场,因此需要借助Fluent软件来模拟烟气流经换热器管排的温度场.由于不需要研究流动的湍流形态,故以稳态流场下的温度场为研究对象,并将其作为背景流对非均匀温度场下的声传播行为进行研究.
将非均匀温度场中介质的密度和当地声速定义为欧几里得空间坐标的函数,可以得到非均匀介质中的声波波动方程[4]:
(11)
式中:c(x)、ρ(x)和p(x)分别为非均匀介质中某点的当地声速、密度和压力.
1.3.2 管阵列模型选取
换热器管道外径取50 mm,过热器与再热器的横向节距与管道直径比S1/d=2,纵向节距与管道直径比S2/d=4;省煤器的横向节距与管道直径比S1/d=2,纵向节距与管道直径比S2/d=2.
由于过热器和再热器布置在烟气温度为973.15~1 073.15 K的环境中,选取换热器管道内工质温度为813.15 K,烟气温度为1 073.15 K,烟气流速为8 m/s.
以5×5管阵列为研究对象,其非均匀温度场通过数值模拟获得,均匀温度场的参照对象为5×5管阵列,管阵列布置方式为过热器与再热器对流式布置,其中晶格常数a=100 mm,b=200 mm.
图4给出了均匀温度场与非均匀温度场的声压级(SPL)曲线.由图4可知,对于低频段,温度场的非均匀性对管阵列声传播特性的影响不大,两者的SPL曲线基本吻合,然而对于高频段,非均匀温度场导致多条声禁带向低频段移动,对于6 000~8 000 Hz频段,非均匀温度场的声禁带传递损失小于均匀温度场;8 000~10 000 Hz频段的声禁带数量增加,且传递损失增大.因此,非均匀温度场对管阵列声传播特性的影响主要集中在高频段,而电站锅炉压力管道泄漏信号属于宽带噪声信号,对管阵列声传播行为进行研究时加入非均匀温度场是必要的.
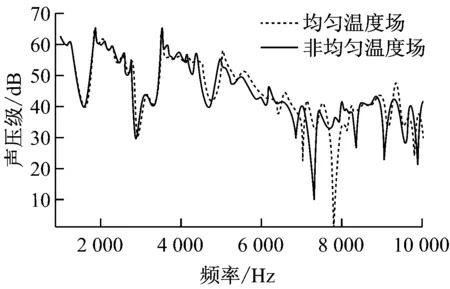
图4 均匀温度场与非均匀温度场的SPL曲线
图5给出了5×5管阵列数值模拟结果.由图5可知,烟气下风向温度逐渐降低,当地声速随之变化;在高频段,声传播呈现间断性,盲区散布于二维空间内各位置.
对于大型电站锅炉实际情况而言,管排数往往达到数十排,因此有必要对大管排数管阵列进行数值模拟和分析.数值模型采用管排布置方式为8列以及5、10、15、20、25排,其中列方向为周期性边界.
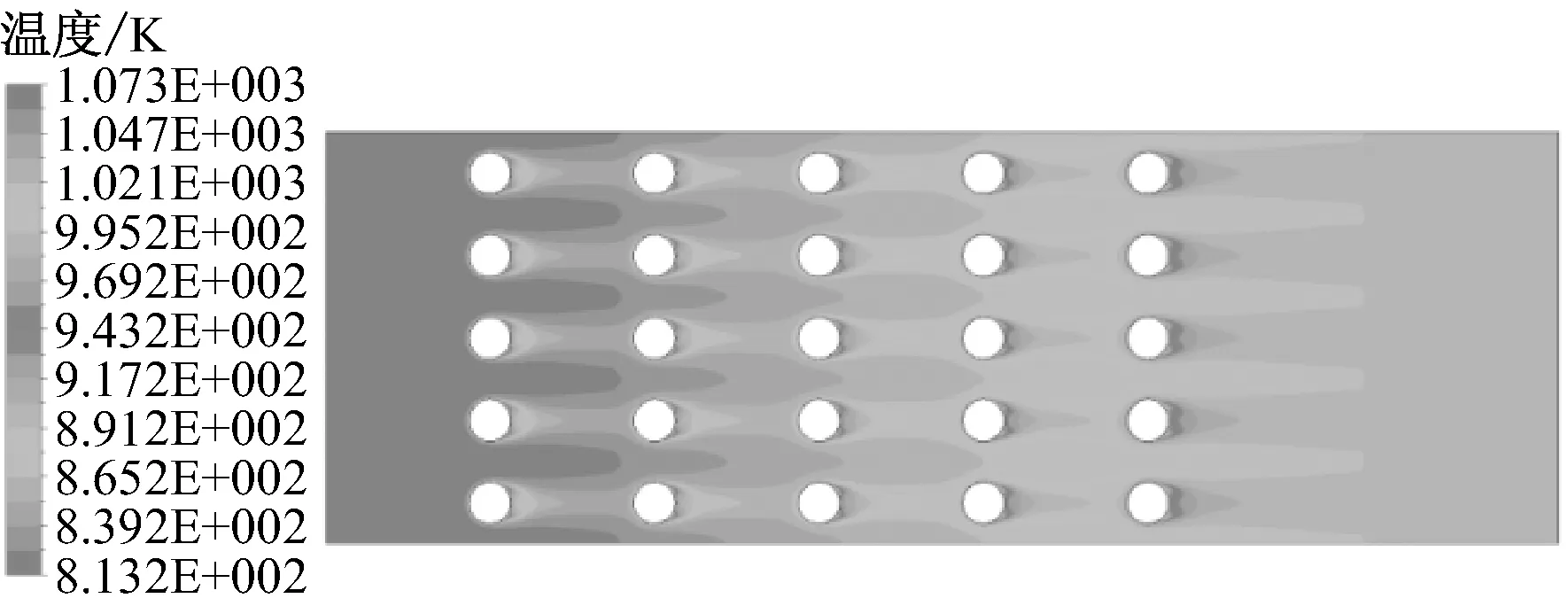
(a)温度场

(b)当地声速
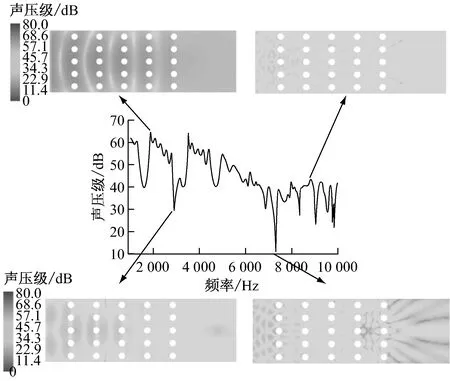
(c)(1.1,0)处SPL曲线及波峰、波谷声传播云图
图6给出了大管排数下SPL曲线的对比.由图6可知,当管排数小于20时,不完全声禁带的声压级随管排数增加而逐渐降低.当管排数大于20时,如图6(c)所示,仅在低频段声禁带部分的SPL曲线有较小差异,在高频段基本吻合.同时可以得出,声禁带并不随管排数的增加而改变,差异仅存在于传递损失.
1.3.3 布置方式对管阵列声传播特性的影响
由于管阵列在错列布置时,周期性边界处偶数排存在半界面管道,为防止半界面管道对数值模拟产生影响,将管阵列数量扩展为8×8,分别对对流式过热器和省煤器的顺列及错列布置方式进行对比研究.
8×8管阵列的顺列布置方式与5×5管阵列布置方式相同,仅在数量上进行扩充,8×8管阵列错列布置方式如图7所示.图8给出了对流式过热器顺列与错列布置方式下声传播特性的对比.由图8可知,在对流式过热器的稀疏布置方式下,顺列与错列布置方式对5 000 Hz以下低频段声传播特性的影响不明显;对于5 000~8 000 Hz频段,错列布置方式的传递损失大于顺列布置方式;在8 000~10 000 Hz频段,错列布置方式不完全声禁带数量要多于顺列布置方式,但顺列布置方式在9 040 Hz与9 360 Hz附近的传递损失较为严重.

(a)5、10、15排管阵列SPL曲线

(b)15、25排管阵列SPL曲线

(c)20、25排管阵列SPL曲线

图7 8×8管阵列错列布置方式
图9给出了省煤器顺列与错列布置方式下声传播特性的对比.由图9可知,在省煤器的稠密布置方式下,错列布置方式下在2 000 Hz附近低频段的传递损失较为严重;对于4 000~7 000 Hz频段,错列布置方式的传递损失与顺列布置方式相似,但不完全声禁带数量要少于顺列布置方式;对于7 000 Hz以上的高频段,错列布置方式的传递损失较顺列布置方式严重.
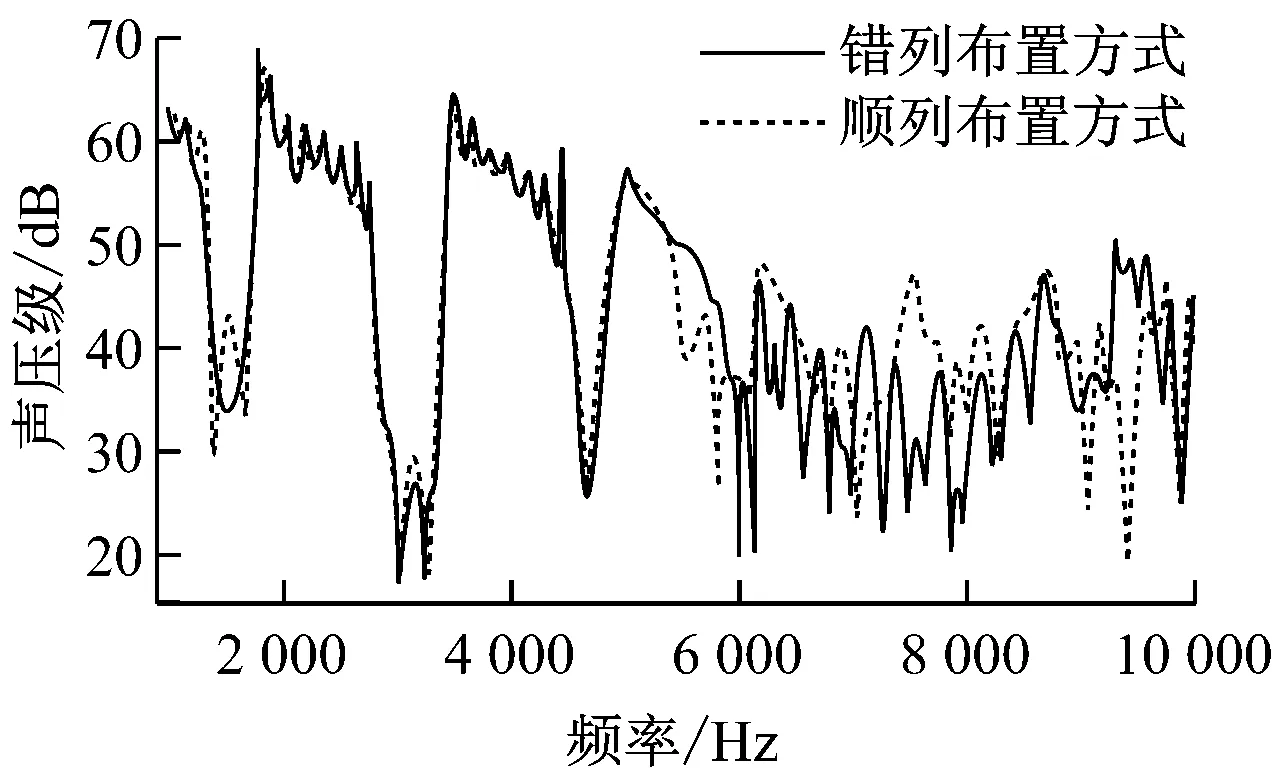
图8 对流式过热器顺列与错列布置方式下声传播特性的对比
Fig.8 Acoustic propagation characteristics in sequence and stagger arrangement for convective superheater
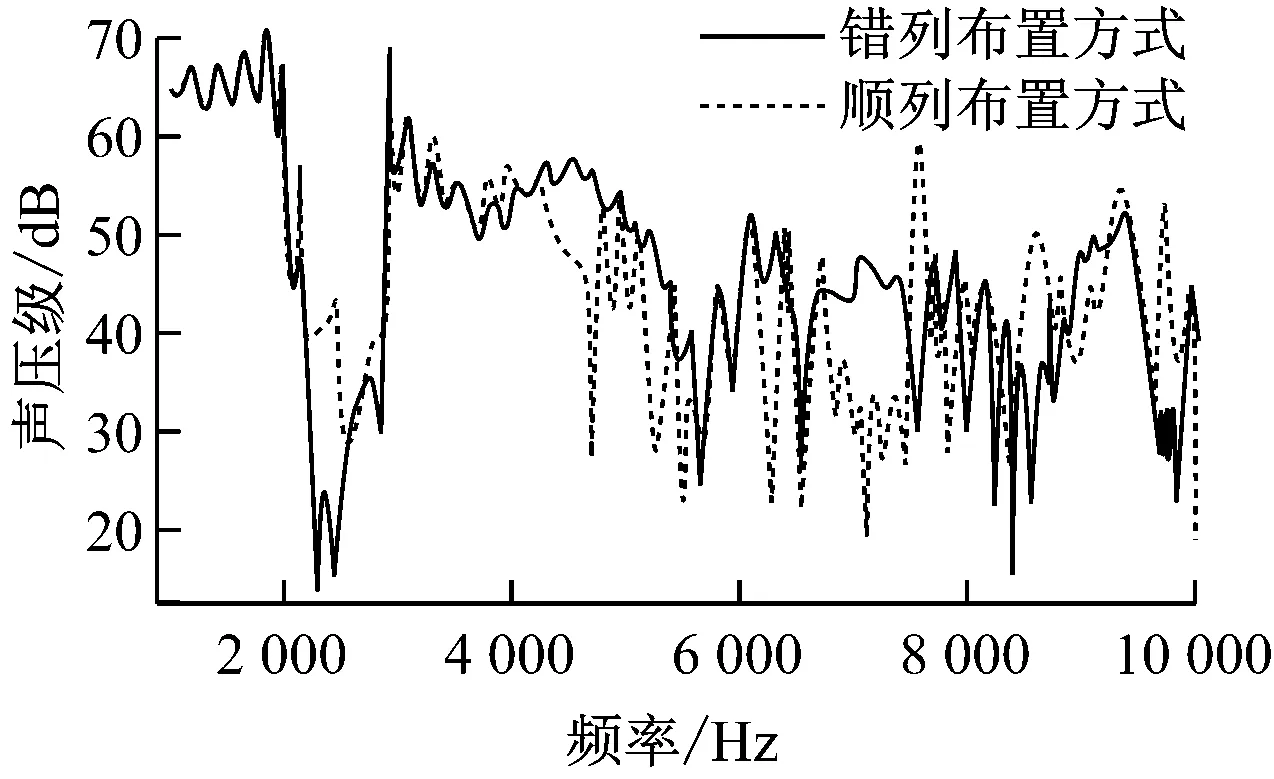
图9 省煤器顺列与错列布置方式下声传播特性的对比
Fig.9 Acoustic propagation characteristics in sequence and stagger arrangement for economizer
2 管阵列内时延值测量
2.1 管阵列内声波衍射行为
声波在传播过程中服从惠更斯-菲涅耳原理,该原理表明当声波遇到障碍物时存在绕射行为,并在障碍物背侧继续传播.声波衍射行为与障碍物特征尺寸、波长存在如下关系式:
ka=2πr/λ
(12)
式中:ka为物体线度与声波波长的相对大小;r为障碍物特征尺寸(如圆柱体则为半径);λ为某一频率对应的波长.
ka的大小决定了衍射行为在声传播中所占的比重,当ka<<1时,存在较强的衍射行为;当ka=1时,存在部分衍射行为;当ka>>1时,几乎不存在衍射行为,障碍物背侧有明显的声影.在烟气温度为1 073.15 K,当地声速为643.78 m/s时,不同管径及频率下对应的ka值见表1.
由表1可以看出,19 mm管径在3 000 Hz以下的声信号具有良好的衍射特性,而3 000 Hz以上的声信号反射行为占主导地位;而对于25 mm和30 mm管径,1 500 Hz以下的声信号具有良好的衍射特性.
表1 不同管径及频率下对应的ka值
Tab.1 Values ofkaat different sizes of tubes and different frequencies

管径/mm频率/Hz100015003000600010000190.190.280.561.111.85250.240.370.731.462.44300.290.440.881.762.93
2.2 基于快速EEMD处理的管阵列内时延值测量
2.2.1 快速EEMD算法
对信号进行经验模态分解(EMD)[5-6]处理时需要满足2个条件:(1)对于整个数据序列,过零点个数与极值点个数至多差1个或者相等;(2)对于信号中任意一点,信号局部极小值和局部极大值所定义的下包络线和上包络线具有零均值的特点.
在满足上述条件的情况下,EMD算法可以通过以下步骤将信号拆分为若干模态分量(IMF)和一个残余项.
(1)对泄漏信号x(t)时域波形取极大值点,通过3次样条插值获得上包络线u(t),通过同样方法获得极小值点所确定的下包络线d(t),同时记m(t)为上下包络线的均值,即m(t)=[d(t)+u(t)]/2.
(2)定义h1(t)=x(t)-m(t),在处理非平稳信号和非线性信号的过程中,h1(t)通常无法满足EMD处理时所需的2个前提条件,对此需要重复执行步骤(1)和步骤(2),直至h1(t)满足EMD处理的前提条件为止,将满足条件的h1(t)记为h1IMF(t).
(3)将泄漏信号原始数据减去h1IMF(t),获得剩余数据记作r1(t),即r1(t)=x(t)-h1IMF(t).
(4)将步骤(3)所得剩余数据r1(t)作为后续处理的原始数据,重复步骤(1)~步骤(3),获得n个IMF:
(13)
EMD处理拆分过程的停止准则[7]为:定义标准差Sd,使得2次连续处理结果的标准差限定在一定范围内,Sd的取值一般为0.2~0.3.Sd的表达式为
(14)
式中:T为泄漏信号的时间尺度;hik(t)为第i个IMF第k次筛选的次数序列.
泄漏信号经过上述迭代过程被分解为n个IMF和一个残余函数rn(t):
(15)
其中,n个IMF包含各时间尺度的特征信号,残余函数rn(t)表示原泄漏信号趋势量信息.
在实际应用过程中,EMD算法存在模态混叠的缺点,即某个IMF包含了时间尺度差别较大的特征信息或者相近的时间尺度被拆分到不同的IMF中.为解决该问题,Wu等[8]提出了集合经验模态分解(EEMD),该算法的特点在于将噪声作为辅助分析应用于EMD算法中,通过促进抗混分解能够有效抑制模态混叠现象.
在EMD处理的原始步骤基础上,针对每次分解过程,EEMD算法均加入高斯白噪声,其中噪声幅值标准差为常数,均值为0.然而,由于高斯白噪声的加入,在EEMD处理过程中IMF的筛选较为耗时,不利于在线监测,故引入快速EEMD算法,该算法通过减少取样的方式来减少计算时间,在一定程度上提高了EEMD算法的工程应用价值.
2.2.2 管阵列低频段声信号时延值测量可行性分析
由于低频段声信号具有良好的衍射特性,同时声信号传播遵循费马定理,即声波在两点间传播沿最短路径.管阵列中声信号传播路径如图10所示,即声波沿图中虚线传播至声感知设备.在时延值测量中,若选用低频段声信号作为分析对象,则可以获得泄漏信号直达2个声感知设备之间的传播时间差(即时延值),能够有效避免中高频段声信号所带来的管道间反射干扰.

图10 声传播衍射行为示意图
Fig.10 Diffraction behavior of acoustic propagation
2.2.3 单列管排低频段声信号时延值测量实验
首先进行无管阵列情况下当地声速标定,标定方法如下:(1)将2个声感知设备(即声波接收器)置于间隔1 m的位置;(2)采用电声源发出的高斯白噪声作为声源,将喇叭置于任一段声感知设备的外侧;(3)测量时延值;(4)通过距离与时延值的关系获得当地声速.经测量,实验室内当地声速为340 m/s.
将直径为0.1 m的声波导管直立于地面,声源选高斯白噪声,2个声感知设备分别置于两端的声波导管外侧且贴壁,调节2个声感知设备的直线距离为1 m,中间等间距放置2个声波导管,进行时延值测量,所得互相关图形如图11所示.
对比图11可知,在宽频带声源的时延值测量中,由于管径较粗,具有良好衍射行为的声信号频段较低,而中高频段在实验室内的混响现象较为严重,且在原始测量信号中占主导地位,因此采用全频段对测量信号进行互相关时获得的时延值误差较大,直接影响了定位结果,该误差下测量所得2个声感知设备的距离为2.64 m,而声信号实际传播路径(含绕射路径)长度为1.029 m.使用小波分解方法[9]对原始测量信号进行处理,经筛选后选择db5小波基第5层分解作为互相关输入数据,得到的时延值为0.003 56 s,对应的测量距离为1.211 m,误差为0.177 m,相对误差为17.7%,误差较大,无法满足工程误差精度要求;经过快速EEMD处理后,选用较低频段的IMF7进行互相关分析,可以得出较为准确的时延值(0.003 115 s),对应的测量距离为1.056 m,误差为0.027 m,相对误差为2.6%,满足工程误差精度要求.

(a)原始测量信号互相关图形
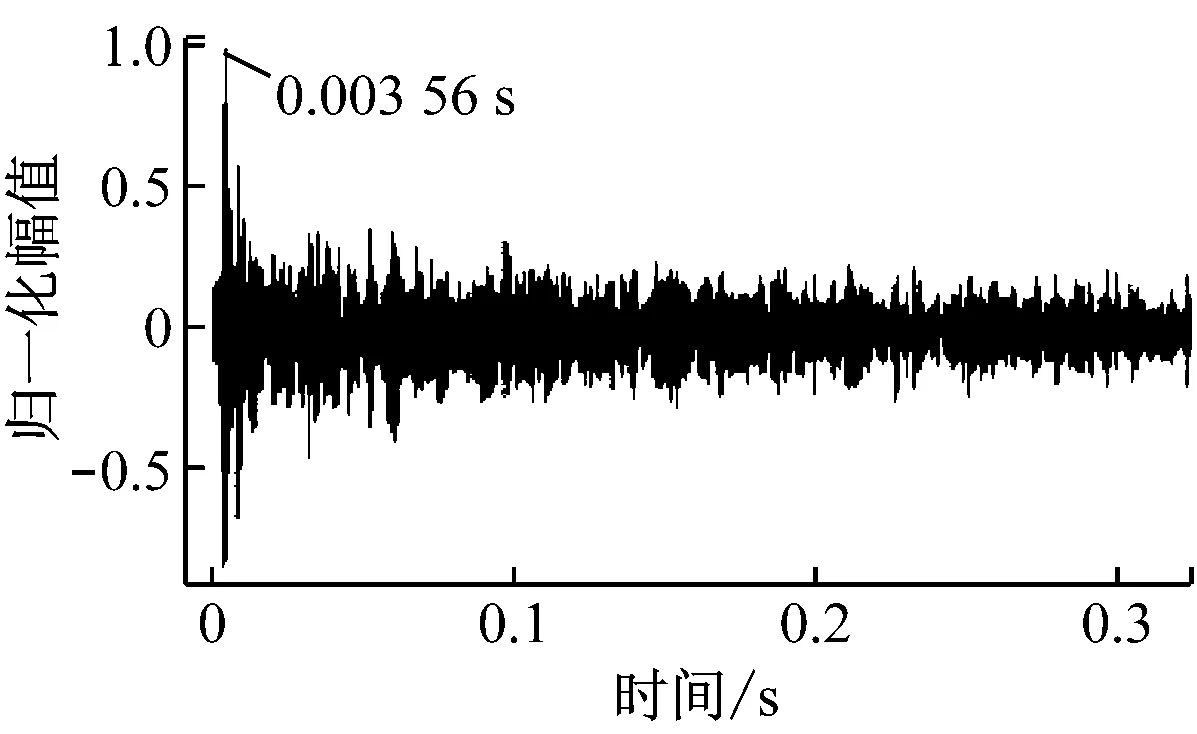
(b)db5小波基第5层分解处理后互相关图形

(c)快速EEMD处理后所得IMF7互相关图形
2.2.4 管阵列低频段声信号时延值测量实验
为接近真实情况下水平烟道及尾部烟道内管阵列布置结构,搭建管阵列实验台,管阵列横向长度为2.96 m,纵向长度为2.96 m,高度为2.9 m,管道横向节距为0.1 m,纵向节距为0.1 m,直径为0.025 m.纵向布置30根不锈钢管,沿高度方向布置29根不锈钢管,共计870根管道,如图12所示.

图12 管阵列实验台
对管阵列内声信号时延值测量进行4组实验,具体布置方式及测量方法如下.
实验一:管阵列内1 m距离时延值测量,将2个声感知设备分别置于管阵列最外侧及管阵列内部纵向距离1 m处,高度为1.5 m,2个声感知设备与地面平行,直线距离为1 m,均贴壁,选择高斯白噪声作为声源.经快速EEMD处理后互相关图形如图13所示.所测得的时延值为0.002 98 s,对应测量距离为1.013 m,2个测点间声信号实际传播路径长度差值为1.007 m,误差为0.006 m,相对误差为0.6%,满足工程误差精度要求.
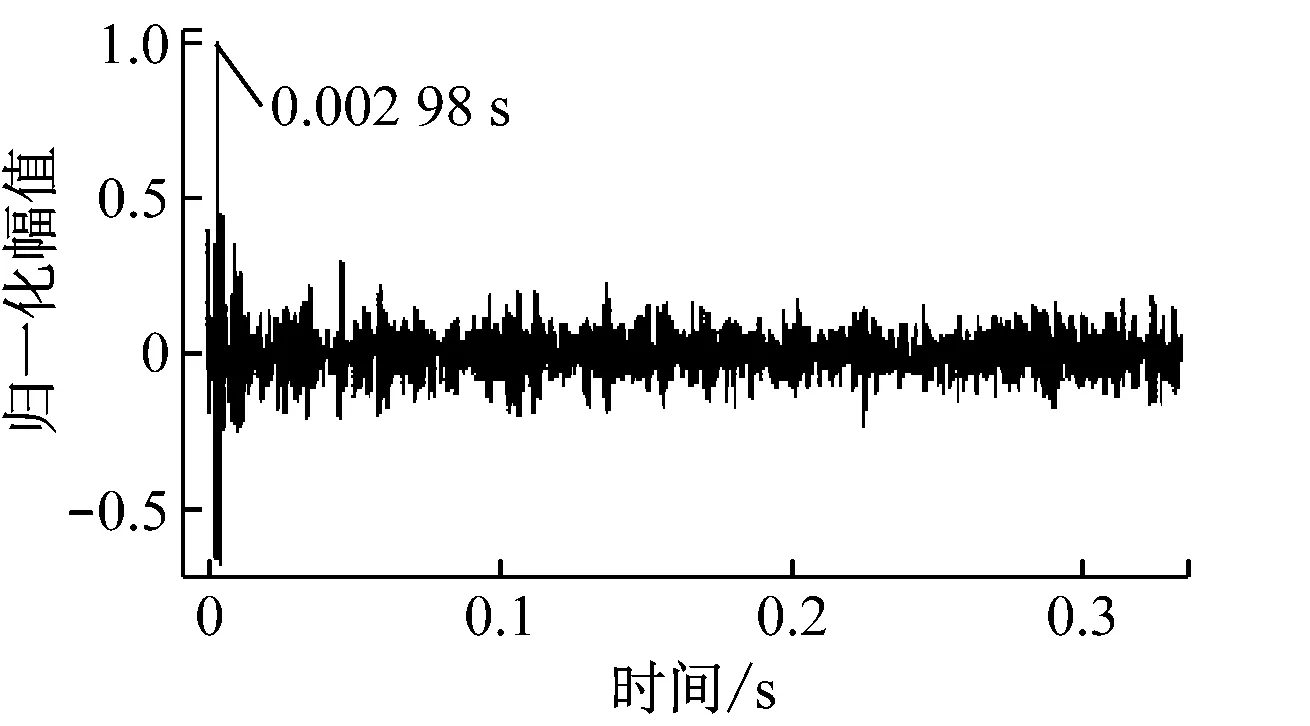
图13 实验一中快速EEMD处理后所得IMF6互相关图形
Fig.13 Results of IMF6 with GCC disposed by Fast EEMD in experiment 1
实验二:改变测点位置,2个测点间的纵向距离为3.16 m,横向距离为0 m,高度差为0.75 m,由勾股定理得出2个测点间的直线距离为3.248 m,选择高斯白噪声作为声源.经快速EEMD处理后互相关图形如图14所示.所测得的时延值为0.009 72 s,对应的测量距离为3.304 m,误差为0.056 m,相对误差为1.7%,满足工程误差精度要求.
实验三:改变测点位置,2个测点间的纵向距离为2.96 m,横向距离为0 m,高度差为1.3 m,由勾股定理得出2个测点间的直线距离为3.23 m,选择高斯白噪声作为声源.经快速EEMD处理后互相关图形如图15所示.所测得的时延值为0.009 69 s,对应的测量距离为3.29 m,误差为0.06 m,相对误差为2.0%,满足工程误差精度要求.

图14 实验二中快速EEMD处理后所得IMF6互相关图形
Fig.14 Results of IMF6 with GCC disposed by Fast EEMD in experiment 2

图15 实验三中快速EEMD处理后所得IMF6互相关图形
Fig.15 Results of IMF6 with GCC disposed by Fast EEMD in experiment 3
实验四:测点位置同实验三,改变声源位置至另一端测点,进行反向测量.经快速EEMD处理后互相关图形如图16所示.所测得的时延值为0.009 44 s,对应的测量距离为3.21 m,误差为0.02 m,相对误差为0.6%,满足工程误差精度要求.

图16 实验四中快速EEMD处理后所得IMF6互相关图形
Fig.16 Results of IMF6 with GCC disposed by Fast EEMD in experiment 4
3 结 论
(1)电站锅炉水平烟道及尾部烟道内管阵列存在明显的声禁带,且非均匀温度场下声禁带向低频段移动,随着管排数增加,声禁带效应明显,在管排数大于20后继续增加管排数,声禁带效应几乎不再受影响.
(2)管道间节距对顺列和错列布置方式下的声传播特性有一定影响,当管道间节距较大时,如对流式过热器,在5 000 Hz以下频段的影响基本不大,然而当管道间节距较小时,如省煤器,即使在2 000 Hz附近的低频段,错列布置方式的传递损失也较为严重.
(3)低频段声信号具有良好的衍射特性,基于快速EEMD处理的互相关结果明显优于小波分解方法,通过搭建管阵列实验台证明该算法在实验室环境下具有一定的可行性,为电站锅炉管阵列内时延值测量提供了参考.
[1] 姜根山,刘月超,安连锁.基于声子晶体理论的炉内管阵列声透射特性数值研究[J].动力工程学报,2014,34(11):850-855.
JIANG Genshan,LIU Yuechao,AN Liansuo.Numerical study on sound transmission through boiler tube arrays based on phononic crystal theory[J].Journal of Chinese Society of Power Engineering,2014,34(11):850-855.
[2] 姜根山.锅炉管道泄漏声行为特性研究[D].保定:华北电力大学,2006.
[3] 姜根山,刘月超,陈朵朵,等.基于声子晶体理论的管阵列声透射特性实验研究[J].动力工程学报,2015,35(3):197-204.
JIANG Genshan,LIU Yuechao,CHEN Duoduo,et al.Experimental study on sound transmission across tube arrays based on phononic crystal theory[J].Journal of Chinese Society of Power Engineering,2015,35(3):197-204.
[4] 王治国.MSC.ACTRAN工程声学有限元分析理论与应用[M].北京:国防工业出版社,2007.
[5] 黄建,胡晓光,巩玉楠.基于经验模态分解的高压断路器机械故障诊断方法[J].中国电机工程学报,2011,31(12):108-113.
HUANG Jian,HU Xiaoguang,GONG Yu'nan.Machinery fault diagnosis of high voltage circuit breaker based on empirical mode decomposition[J].Proceedings of the CSEE,2011,31(12):108-113.
[6] HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,1998,454:903-995.
[7] RILLING G,FLANDRIN P,GONÇALVS P.On empirical mode decomposition and its algorithms[C]//Proceedings of the 6th IEEE/EURASIP Workshop on Nonlinear Signal and Image Processing.Grado,Italy:IEEE,2003.
[8] WU Zhaohua,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[9] 许小刚,王松岭,刘锦廉.基于小波包能量分析及改进支持向量机的风机机械故障诊断[J].动力工程学报,2013,33(8):606-612.
XU Xiaogang,WANG Songling,LIU Jinlian.Mechanical fault diagnosis of fan based on wavelet packet energy analysis and improved support vector machine[J].Journal of Chinese Society of Power Engineering,2013,33(8):606-612.
Acoustic Propagation and TDOA Measurement in Tube Arrays of Utility Boiler
ANLiansuo1,FENGQiang1,SHENGuoqing1,JIANGGenshan1,ZHANGShiping1,WANGPeng1,ZHANGHaiyu2
(1.MOE's Key Lab of Condition Monitoring and Control for Power Plant Equipment,School of Energy,Power and Mechanical Engineering,North China Electric Power University,Beijing 102206,China; 2.China Urban Construction Design & Research Institute Co.,Ltd.,Beijing 100120,China)
A study was conducted on acoustic propagation and TDOA measurement in tube arrays of utility boiler,where the propagation characteristics were numerically compared using Fluent software under the conditions of uniform/non-uniform temperature field,and different rows of tubes in different arrangements,while the TDOA in tube arrays was measured on a self-developed test bench by Fast EEMD algorithm.Results show that acoustic band gaps exist in the tube array,which move to low frequency area in non-uniform temperature field.With the rise of tube rows,the effect of acoustic band gap becomes more obvious.Tube pitch has a certain influence on the band rejection in both sequence and stagger arrangement of tubes.Based on Fast EEMD algorithm,effective TDOA can be obtained when low frequency signals are chosen.
utility boiler; tube array; acoustic propagation; TDOA; Fast EEMD
2016-02-01
2016-03-31
国家自然科学基金资助项目(11274111);北京高等学校青年英才计划资助项目(YETP0700);华北电力大学中央高校基本科研业务费专项资金资助项目(2014MS10,2015XS77)
安连锁(1955-),男,河北武邑人,教授,本科,研究方向为电站设备状态监测与控制.冯 强(通信作者),男,博士,电话(Tel.):1366615305;E-mail:493536802@qq.com.
1674-7607(2017)01-0013-08
TK39
A 学科分类号:470.30

