无耦合空间移动并联机构型综合

张彦斌 赵浥夫 李跃松 王增辉 丁 丁

(河南科技大学机电工程学院， 洛阳 471003)

无耦合空间移动并联机构型综合

张彦斌 赵浥夫 李跃松 王增辉 丁 丁

(河南科技大学机电工程学院， 洛阳 471003)

为解决利用一般型综合方法得到的并联机构具有强运动学耦合性的问题，基于驱动力螺旋理论提出了一种无耦合空间移动并联机构型综合的系统方法。首先建立了无耦合移动并联机构运动输入输出关系的数学模型；然后根据机构速度雅可比矩阵为对角阵的条件推导出分支运动链驱动力螺旋和主动运动螺旋的形式；再根据互易积原理建立了分支运动链非主动运动螺旋的确定方法，给出了分支运动链型综合准则和步骤；最后将所综合的3条分支运动链按照指定的配置方式将动平台和静平台连接起来即可得到具有预期运动特性的机构。本文共综合出60种具有对称结构的无耦合空间移动并联机构，其中非过约束机构有47种，含有惰性副的有29种。所得到的部分机构的雅可比矩阵为单位阵，且其条件数恒等于1。这些机构具有较好的运动和力学传递性能，进一步丰富和完善了并联机构的型综合理论。

并联机构； 型综合； 驱动力螺旋理论； 无耦合； 雅可比矩阵

引言

并联机构因其在运动学性能、刚度和精度性能方面的优点，已得到广泛的应用[1-4]。型综合是并联机构研究领域的重点和难点，也是机构原始创新的理论基石。并联机构的型综合是通过对特定自由度机构可动性的研究，建立运动副配置的理论，从而得到一类新型机构。目前，国际上常用的并联机构型综合的方法有：基于自由度计算公式的列举法[5]、基于位移子群理论的型综合方法[6-7]、基于GF集理论的型综合方法[8]、基于方位特征集的型综合方法[9-11]、基于机构演化的型综合方法[12]和基于螺旋理论的型综合方法[13-14]等。每一种型综合方法各有其自身的优势和特点，但很难使用任何一种方法或理论体系综合出所有结构形式的并联机构。因此各种型综合方法相互补充，共同构成了并联机构的型综合理论体系。

强运动耦合性是一般并联机构的共同特性，即机构动平台的一个输出运动同时由若干个(甚至全部)主动输入联合控制。尽管运动耦合性有助于提高并联机构的刚度和承载能力，但也造成机构运动学解复杂、控制设计困难和工作空间减小，影响并联机构的实际应用。而在承载能力要求不高的应用场合，解耦并联机构有效地解决了耦合性强的难题。目前，已有诸多国内外学者对于解耦并联机构的设计做了大量工作与研究[15-20]。

本文基于驱动力螺旋理论提出无耦合空间移动并联机构分支运动链的构型理论，从而建立无耦合空间移动并联机构的型综合方法。

1 理论基础

1.1 螺旋

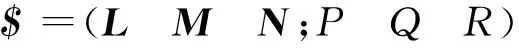
1.2 互易螺旋

若2个旋量$和$r(图1)满足以下条件，则可以称他们为互易螺旋，或称为反螺旋，即

$∘$r=$(Π$r)T=SSr0+S0Sr=0

(1)

其中

式中O——3×3阶0矩阵I3——3×3阶单位阵 ∘ ——旋量互易积Π——对偶算子

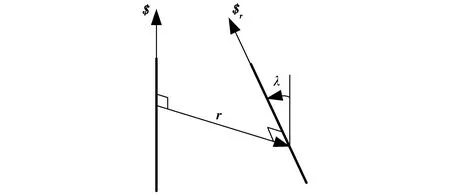
图1 互易螺旋Fig.1 Reciprocal screws

物理意义上讲，当一个旋量表示刚体的运动螺旋，另一个表示刚体受到的力螺旋时，互易积表示力螺旋对运动螺旋所做的瞬时功。如果互易积等于零，则表示该刚体此时的运动状态不受此力螺旋的影响，即力螺旋在该运动方向上不做功。

根据互易积原理可以推导得2个螺旋的互易条件，有

(2)

式中h、hr——螺旋$和$r的节距λ——两旋量轴线的夹角，规定由$到$r为其正方向

r——两旋量轴线间的垂直距离

对于线矢量和偶矢量，由式(2)可以得出互易的形式：①两轴线相交或平行的线矢量互为反螺旋。②两轴线相互垂直的线矢量和偶矢量互为反螺旋。③任意2个偶矢量互为反螺旋。

1.3 驱动力螺旋

物理意义上看，驱动力螺旋是由分支运动链中的主动副施加到动平台上的一个力螺旋，即主动副向动平台提供的一个驱动力。故驱动力螺旋与同一分支运动链中除主动运动螺旋外的其他所有运动螺旋都互为反螺旋，其中主动运动螺旋为分支主动副所对应的运动螺旋。

(3)

2 无耦合并联机构输入-输出关系的数学模型

并联机构动平台的瞬时输出运动可用机构分支运动链的运动螺旋系表示，即

(4)

式中v——机构动平台输出的广义速度矢量 $ji——第i条分支中的第j个单自由度关节的运动螺旋

Fi——第i条分支的连接度

如果用第i条分支的驱动力螺旋$ai与式(4)左右两边同时作互易积，得

(5)

式中 $1i——第i条分支中主动副的运动螺旋(假定每条分支的主动副直接安装在静平台上，即为分支的第一个运动副)

将式(5)改写成矩阵形式，有

(6)

其中

由式(6)可知正雅可比矩阵Jdir为对角阵，若其可逆，则式(6)可改写为

(7)

其中

gi=$ai(Π$1i)T

对于n自由度并联机构，其动平台上不存在寄生运动特定点的独立输出速度数目亦为n，那么输出速度矢量v中存在6-n个零元素。若去除v中的零元素，同时去除正雅可比矩阵Jdir中对应的列元素，那么式(7)将变形为

(8)

(9)

根据驱动力螺旋的定义可知，它是由分支运动链中的主动副施加到动平台上的一个力螺旋，当其为零节距螺旋时(即为线力)，将驱使机构动平台沿线力矢方向产生移动趋势(即产生线位移)；而当其为无穷大节距螺旋时(即为偶力)，将驱使动平台绕偶力矢方向产生转动趋势(即产生角位移)。对于空间移动并联机构，由于其动平台上任一点在运动过程中仅沿标定方向移动，而不会产生角位移(或角速度)，因此机构分支施加到动平台的驱动力螺旋必为零节距螺旋。根据式(9)可进一步写出无耦合空间移动并联机构的运动学方程，为

(10)

式中v1、v2和v3为动平台上一点沿笛卡尔坐标轴线方向的线速度，即这3个速度方向呈正交分布。

3 无耦合空间移动并联机构的分支运动链型综合

3.1 分支运动链型综合准则

并联机构型综合的关键和前提就是其分支运动链的型综合。根据机构的输出运动特性确定分支运动链中运动副的类型、数目和排列次序，以及运动副轴线的配置方位等。尤其是对无耦合空间移动并联机器人机构，要求其一条分支运动链仅为动平台沿某一个特定方向的运动提供驱动力，而对其他方向的运动不提供任何驱动力。因此，建立分支运动链构造的型综合准则成为机构型综合的重要理论基础。本文根据推导的方程(10)建立了无耦合移动并联机构分支运动链的型综合准则和步骤，具体如下：

(1)按照并联机构动平台的运动输出特性，分配各运动分支的控制目标，根据式(10)确定各分支运动链的驱动力螺旋。

(2)根据同一运动分支中的驱动力螺旋与该分支中主动运动螺旋互易积不为零的准则，即gi≠0的条件，确定出各运动分支的主动运动螺旋。

(3)根据驱动力螺旋与同一运动分支中除主动运动螺旋外其他所有运动螺旋都互为反螺旋的特性，列举出分支中所有可能的从动运动螺旋，并基于运动螺旋系最大线性无关组条件，确定运动分支中可能存在的各类运动螺旋的数目。

(4)根据所求出的主动运动螺旋和从动运动螺旋的形式，确定分支运动链中主动副和从动副的类型、数目和配置方位，同时考虑惰性副的存在情况。

(5)按照各运动分支中连接度的不同进行分支运动链的型综合，列举所有可行的分支运动链结构。

3.2 第1条分支运动链的型综合

不失一般性，设第1条分支运动链仅控制机构动平台沿X轴方向的线性移动，即vx=v1。为简化问题的分析，假定运动链中仅含有移动副和转动副2种基本类型，其他多自由度运动副可由相邻基本运动副组合而成。

如图2所示，静坐标系OXYZ的坐标原点O固结于静平台，动坐标系oxyz的坐标原点o固结于动平台，而动坐标系的3个坐标轴与静坐标系的3个坐标轴对应平行。

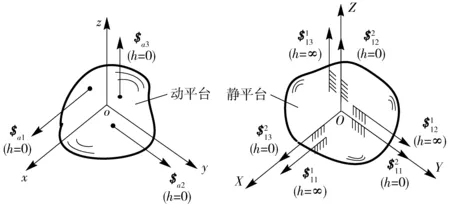
图2 分支驱动力螺旋与主动运动螺旋Fig.2 Actuation wrench screws and actuation twist screws of mechanism limbs

根据式(10)可知，由于机构雅可比矩阵对角线上的第1个元素为非零数值，可确定出第1条分支运动链施加在动平台上的驱动螺旋形式，即

(11)

故该驱动力螺旋为平行于X轴的纯力螺旋，将驱动机构动平台沿X轴方向产生移动趋势。同时，该力螺旋必过坐标点(0,ya1,za1)，于是可计算出Qa1=za1，Ra1=-ya1。

若式(10)矩阵中第1个对角线元素有意义，那么该元素的分母部分必不为零，即

g1=$a1(Π$11)T≠0

(12)

式中$11为第1条分支的主动运动螺旋，即主动副所对应的运动螺旋。$11可能的形式有2种：无穷大节距螺旋或零节距螺旋。

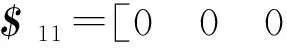
g1=$a1(Π$11)T=L11

(13)

(14)

将式(14)代入式(13)得g1=1，满足上述分母非零的条件，所以第1条分支的主动运动螺旋可为平行于X轴的无穷大节距螺旋，如图2所示，即该分支的主动副可选为轴线平行于X轴的移动副。

g1=$a1(Π$11)T=P11+za1M11-ya1N11

(15)

根据式(15)可知，g1的值与$11的方向矢量在Y轴和Z轴方向的分量(M11和N11)有关，而与其在X轴方向的分量L11无关，因此可取L11=0。由于主动螺旋$11固定于静平台上，故可将静坐标系原点O落在该螺旋轴线上，即$11通过该坐标原点，那么有P11=Q11=R11=0。因而式(15)可化简为

g1=za1M11-ya1N11

(16)

(17)

将式(17)代入式(16)得，g1=za1。因此，只要za1不等于零，g1值就不为零，也就满足上述分母不为零的条件。所以第1条分支的主动运动螺旋也可为平行于Y轴的零节距螺旋(图2)，即该分支的主动副也可选为轴线平行于Y轴的转动副。

至此，确定了第1条分支运动链的所有可行的主动运动螺旋形式，从而也确定了该分支主动副的类型及其装配方位。

根据驱动力螺旋与同一条分支运动链中所有非主动运动螺旋互为反螺旋的特点，以及所选取的主动运动螺旋的形式，那么可确定分支中非主动螺旋的类型。

(Ⅰ-1) 平行于X轴的零节距螺旋，其数量至少为2，最多为3，此类螺旋所组成的螺旋系可直接或通过无穷大节距螺旋与动平台相连。

(Ⅰ-2) 垂直于X轴的无穷大节距螺旋，其数量最多为2，此类螺旋可布置在分支螺旋系中的任何位置。

(Ⅰ-3) 与驱动力螺旋$a1轴线相交的零节距螺旋，其数量最多为2，这种运动螺旋对机构的运动性能不起任何作用，因此称为惰性运动螺旋。

(Ⅱ-1) 平行于X轴的零节距螺旋，其数量至少为2，最多为3，此类螺旋所组成的螺旋系可直接或通过无穷大节距螺旋与动平台相连，但该螺旋系中不能插入任何可动零节距螺旋系。

(Ⅱ-2) 垂直于X轴的无穷大节距螺旋，其数量最多为2，但若其数量为2时所组成的螺旋系不能放在2个非惰性零节距螺旋中间。

(Ⅱ-3) 与驱动力螺旋$a1轴线相交且平行于主动螺旋$11轴线的零节距螺旋，其数量有且仅有一个。

(Ⅱ-4) 与驱动力螺旋$a1轴线相交且垂直于主动螺旋$11轴线的零节距螺旋，该螺旋为惰性运动螺旋。

当运动分支运动链中的主动运动螺旋和可能的非主动运动螺旋确定后，便可确定出分支的主动副和可能的非主动副的类型、数目，以及这些运动副的配置方位。然后按照运动分支连接度Fc的不同，列举了不含有惰性副的基本分支运动链结构，共有3P、2P2R、1P3R、1P4R和5R 5种。在不含有惰性副的分支中可插入一个与分支驱动力螺旋$ai轴线相交的转动副R即可得到含有惰性副的运动链，基本类型有2P3R、1P4R、1P5R和6R 4种。虽然惰性副的存在并不能改变机构的运动学性能，但能增加运动分支的连接度以降低机构的过约束数和装配要求。

3.3 第2条分支运动链的型综合

设第2条分支运动链仅控制机构动平台沿Y轴方向的线性移动，即vy=v2。根据机构雅可比矩阵对角线上第2元素为非零的条件，可确定出该分支施加到动平台的驱动力螺旋$a2，且有

(18)

该驱动力螺旋为平行于Y轴的纯力螺旋，驱动动平台沿Y轴方向产生移动趋势。同时，该力螺旋必经过静坐标系中的点(xa2,o,za2),于是可计算出Pa2=-za2,Ra2=xa2，若式(10)矩阵中第2个对角线

表1 无耦合移动并联机构的分支运动链类型及结构
Tab.1 Types and structures of limb for uncoupled spatial translational parallel mechanism

连接度数Fc类型序号基本分支结构含有多自由度运动副的分支结构主动副为Pa分支结构33P1PuPvPw42P2R211PuPvRwRwPuRuPnRuCtuPnRuPuRuRuPvCtuRuPvRvRvPvPwRvCvPwPaPvPwRvPvRvPwCrvRvPw1P3R1213PuRuRuRuCtuRuRu51P4R1432PuRuRuRuRvPuRuRuUuv;CtuRuRuRv;CtuRuUuv;CtuUuvRu;PuUuvRuRu;PuUuvRuRuRvRvRuRuPwRvUvuRuPwPaRuRuPwRvRvRuPnRuRvUvuPnRuPaRuPnRuRvRvPvRuRuRvCvRuRuPaPvRuRuRvPvRvRuRuCrvRvRuRu;CrvUvuRu2P3R3357PuPvRuRuRvPuPvRuUuv;PuPvUvuRu;PuCvRuRuPuRuPnRuRvPuRuPnUuv;PuRuCvRu;CuPnUuv;CuRvPnRu;CtuCnRu;CtuPnRuRv;PuUuvPnRuPuRuRuPvRvPuRuRuCv;CtuRuPvRv;CtuRuCv;CtuUuvPv;PuRuUuvPu;PuUuvRuPv;RvRvPwPvRuRvUvuPwPvPaPwPvRuRvPvRvPwRuCrvRvPwRu;CrvUvuPw5R5760RvRvRuRuRuRvUvuRuRuPaRuRuRu61P5R6181RvRvRwPwRuRuRvUvwPwRuRu;RvRvCwRuRuPaRwPwRuRu;PaCwRuRuRvRvRwRuRuPwRvRvUwuRuPw;RvUvwRuRuPw;RvSRuPwPaRwRuRuPw;PaUwxRuPwRvRvRwRuPnRuRvUvwRuPnRu;RvSPnRu;RvRvUwuPnRuPaRwRuPnRu;PaUwuPnRuRvPvRyRwRuRuCrvRvRwRuRu;CrvUvwRuRu;CrvSRu6R8287RvRvRwRuRuRuRvUvwRuRuRu;RvRvUuwRuRu;RvSRuRuPaRwRuRuRu;PaUuwRuRu

元素有意义，该元素的分母部分也不能为零，即

g2=$a2(Π$12)T≠0

(19)

式中$12为第2条分支的主动运动螺旋，其可能的形式也是2种：无穷大节距螺旋或零节距螺旋。采用与求解第1条分支主动运动螺旋类似的方法便可确定第2条分支的主动运动螺旋形式，有

(20)

或

(21)

式(20)表明第2条分支的主动运动螺旋为平行于Y轴的无穷大节距螺旋(图2)，即该分支主动副可为沿Y轴配置的转动副。式(21)则表明该分支的主动螺旋也可为平行于Z轴的零节距螺旋，即分支主动副为轴线平行于Z轴转动副。

当第2条分支的驱动力螺旋$a2、主动运动螺旋$12的形式确定后，根据螺旋互易积原理便可确定出所有可行的非主动运动螺旋的类型。具体如下：

(Ⅰ-1) 平行于Y轴的零节距螺旋，其数量至少为2，最多为3，此类螺旋所组成的螺旋系可直接或通过无穷大节距螺旋与动平台相连。

(Ⅰ-2) 垂直于Y轴的无穷大节距螺旋，其数量最多为2，此类螺旋可布置在分支螺旋系中的任何位置。

(Ⅰ-3) 与驱动力螺旋$a2轴线相交的零节距螺旋，其数量最多为2，这种运动螺旋对机构的运动性能不起任何作用，因此称为惰性螺旋。

(Ⅱ-1) 平行于Y轴的零节距螺旋，其数量至少为2，最多为3，此类螺旋所组成的螺旋系可直接或通过无穷大节距螺旋与动平台相连，但该螺旋系中不能插入任何可动零节距螺旋系。

(Ⅱ-2) 垂直于Y轴的无穷大节距螺旋，其数量最多为2，但若其数量为2时所组成的螺旋系不能放在2个非惰性零节距螺旋中间。

(Ⅱ-3) 与驱动力螺旋$a2轴线相交且平行于主动运动螺旋$12轴线的零节距螺旋，其数量有且仅有一个。

(Ⅱ-4) 与驱动力螺旋$a2轴线相交且垂直于主动运动螺旋$12轴线的零节距螺旋，该螺旋为惰性螺旋。

当分支主动运动螺旋、非主动运动螺旋的形式确定后，便可按照分支连接度的不同综合出所有可行的分支运动链结构。因与第1条分支具有相同的拓扑结构，令表1中的u=y，v=z，w=x，便可得到第2条支链。

3.4 第3条分支运动链的型综合

设第3条分支运动链仅控制机构动平台沿z轴方向的线性移动，即vz=v3。利用与前2条分支运动链型综合相同的方法列举出第2条分支的运动链结构，令表1中的u=z，v=x，w=y，便可得到第3条支链，这里不再详述综合过程。

4 无耦合空间移动并联机构型综合

分支运动链型综合完成后，从3条分支中各取一条按照分支运动链的配置要求将动平台和静平台连接起来就可以得到预期的无耦合空间移动并联机器人机构，但在选取运动链时必须考虑构成机构的3条分支的连接度总数。非过约束并联机构的分支连接度应满足

(22)

式中F——机构连接度总数Fci——第i条分支连接度数m——机构分支数M——机构自由度数d——机构阶数l——机构独立回路数

对于非过约束空间移动并联机构，m=3，M=3，λ=6，l=2，将这些数据代入式(22)可计算得F=15。因此，在分支运动链的选择时，3条分支运动链的连接度之和必须小于或等于15。当3条分支运动链的连接度之和小于15时，该机构为过约束并联机构；而当3条分支运动链的连接度之和等于15时，该机构为非过约束并联机构。同时需要注意的是，如果分支中含有惰性副，相邻分支中的惰性副轴线应相互垂直。

根据表1得到的分支运动链结构，本文共可综合出60种具有对称结构的无耦合空间移动并联机构，其中非过约束机构有47种，含有惰性副的有29种。而只要满足连接度约束条件，便可得到更多的非对称机构。图3为综合出的一种非过约束3-RRRPR机构，该机构的运动学表达式为

(23)

图3 无耦合3-RRRPR移动并联机构Fig.3 Uncoupled 3-RRRPR translational parallel mechanism

由式(23)可知，机构的雅可比矩阵为对角阵，机构动平台的一个线性输出运动仅由一个关节的转动输入运动控制，故该机构为无耦合移动并联机构。

(24)

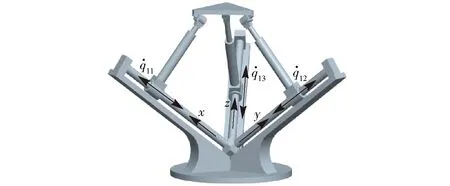
图4 无耦合移动并联机构Fig.

根据式(24)可知，该机构的运动雅可比矩阵不仅为对角阵，而且还是单位阵，因此该机构在整个工作空间内表现为完全各向同性，即机构在工作空间内沿任何方向的运动学和力学性能皆相同。此类机构在运动和力传递过程中不会失真，是最为理想的运动结构形式。

5 结束语

基于驱动力螺旋理论建立无耦合移动并联机构的型综合系统方法，从理论上给出了一条分支运动链控制机构动平台沿某一方向移动时主动副的选取依据，建立了分支运动链中可动非主动副的选取原则和配置方法。利用所提出的方法综合出多种无耦合移动并联机构，其雅可比矩阵为对角阵，即动平台的一个输出运动仅由一个主动副的输入运动控制，解决了一般并联机构运动学和动力学耦合性强的弱点。特别是当采用线性移动作为主动输入时，机构的雅可比矩阵为单位阵，因此在整个工作空间内机构表现为完全各向同性。本文所做的研究不仅可以应用于无耦合空间移动并联机构的构型设计，而且还可以应用于动平台含有转动输出元素的无耦合并联机构的型综合。

1 赵磊, 刘巍, 巩岩. 预紧式Stewart结构六维力/力矩传感器[J]. 光学精密工程, 2011, 19(12): 2954-2962. ZHAO Lei, LIU Wei, GONG Yan. Pre-stressed six-axis force/torque sensor based on Stewart platform[J]. Optics and Precision Engineering, 2011, 19(12): 2954-2962.(in Chinese)

2 蔡赟, 张邦成, 姚禹. 3PTT-2R串并联数控机床动力学耦合特性研究[J/OL]. 农业机械学报, 2015, 46(12): 362-369. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20151249&flag=1. DOI：10.6041/j.issn.1000-1298.2015.12.049. CAI Yun, ZHANG Bangcheng, YAO Yu. Dynamics coupling characteristics of 3PTT-2R NC serial-parallel machine tool[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 362-369.(in Chinese)

3 鹿玲, 姚建涛, 顾伟栋, 等. 基于 Kane 方程的冗余驱动 5UPS/PRPU 并联机床动力学分析[J/OL]. 农业机械学报, 2016, 47(6): 366-372. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160648&flag=1. DOI：10.6041/j.issn.1000-1298.2016.06.048. LU Ling, YAO Jiantao, GU Weidong, et al. Dynamics analysis of 5UPS/PRPU parallel machine tool with redundant actuation based on Kane equation[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 366-372.(in Chinese)

4 朱伟, 汪源, 沈惠平, 等. 仿腕关节柔顺并联打磨机器人设计与试验[J/OL]. 农业机械学报, 2016, 47(2): 402-407. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160254&flag=1. DOI：10.6041/j.issn.1000-1298.2016.02.054. ZHU Wei, WANG Yuan, SHEN Huiping, et al. Design and experiment of compliant parallel humanoid wrist joint polishing robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 402-407.(in Chinese)

5 HESS-COELHO T A. Topological synthesis of a parallel wrist mechanism[J]. ASME Journal of Mechanical Design, 2006, 128(1): 230-235.

6 YU J J, DAI J S, BI S, et al. Numeration and type synthesis of 3-DOF orthogonal translational parallel manipulators[J]. Progress in Natural Science, 2008, 18(5): 563-574.

8 GAO F, YANG J L, GE Q D. Type synthesis of parallel mechanisms having the second classGFsets and two dimensional rotations[J]. ASME Journal of Mechanisms and Robotics, 2011, 3(1): 1-8.

9 沈惠平, 孙驰宇, 朱小蓉, 等. 以基本运动链为单元的并联机构拓扑结构设计[J/OL]. 农业机械学报, 2015, 46(12): 337-345. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20151246&flag=1. DOI：10.6041/j.issn.1000-1298.2015.12.046. SHEN Huiping, SUN Chiyu, ZHU Xiaorong, et al. Topology structure design of parallel mechanisms based on basic kinematic chains[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(12): 337-345.(in Chinese)

10 朱伟, 沈惠平, 刘晓飞, 等. 含方位特征支链并联机构构型综合与结构优化[J/OL]. 农业机械学报, 2016, 47(8): 378-387. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160850&flag=1. DOI：10.6041/j.issn.1000-1298.2016.08.050. ZHU Wei, SHEN Huiping, LIU Xiaofei, et al. Type synthesis and structure optimization of parallel mechanism with position and orientation characteristics limb[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(8): 378-387.(in Chinese)

11 ZHU X R, YAO X, SHEN H P, et al. Structural synthesis based on POC set for lower-mobility non-overconstrained parallel mechanisms[J]. Mechanisms and Machine Science, 2016, 36: 327-338.

12 FAN C X, LIU H Z, ZHANG Y B. Type synthesis of 2T2R, 1T2R and 2R parallel mechanisms[J]. Mechanism and Machine Theory, 2013, 61(3): 184-190.

13 HUANG Z, LI Q C. Type synthesis of symmetrical lower-mobility parallel mechanisms using the constraint synthesis method[J]. International Journal of Robotics Research, 2003, 19(1): 59-79.

14 KONG X W, GOSSELIN C M. Type synthesis of 3-DOF translational parallel manipulators based on screw theory[J]. ASME Journal of Mechanical Design, 2004, 126(1): 83-92.

15 KONG X W, GOSSELIN C M. Type synthesis of input-output decoupled parallel manipulators[J/OL]. Transactions of the Canadian Society for Machanical Engineering, 2004, 28(2A): 185-196.

16 GOGU G. Structural synthesis of fully-isotropic parallel robots with Schonflies motions via theory of linear transformations and evolutionary morphology [J]. European Journal of Mechanics A/Solids, 2007, 26(2): 242-269.

17 张彦斌, 吴鑫. 完全解耦二维移动二维转动并联机构结构综合[J/OL]. 农业机械学报, 2013, 44(8): 250-256. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130843&flag=1. DOI：10.6041/j.issn.1000-1298.2013.08.043. ZHANG Yanbin, WU Xin. Structural synthesis of fully-decoupled two-translational and two-rotational parallel mechanisms[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(8): 250-256. (in Chinese)

18 ZENG D X, HOU Y L, CHANG W, et al. Type synthesis of the translational decoupled parallel mechanism based on screw theory[J]. Journal of Harbin Institute of Technology University, 2014, 21(1): 84-91.

19 张彦斌, 刘宏昭, 吴鑫. 基于互易螺旋理论的无奇异完全各向同性移动并联机构型综合[J]. 机械工程学报, 2008, 44(10): 83-88. ZHANG Yanbin, LIU Hongzhao, WU Xin. Type synthesis of non-singular fully-isotropic translational parallel mechanisms based on theory of reciprocal screw[J]. Chinese Journal of Mechanical Engineering, 2008, 44(10): 83-88.(in Chinese)

20 秦友蕾, 曹毅, 陈海, 等. 完全解耦3T2R并联机器人构型综合方法[J]. 航空学报, 2016, 37(6): 1983-1991. QIN Youlei, CAO Yi, CHEN Hai, et al. Structural synthesis method of fully decoupled 3T2R parallel robotic manipulators[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1983-1991.(in Chinese)

Structural Synthesis of Uncoupled Spatial Translational Parallel Mechanisms

ZHANG Yanbin ZHAO Yifu LI Yuesong WANG Zenghui DING Ding

(SchoolofMechatronicsEngineering,HenanUniversityofScienceandTechnology,Luoyang471003,China)

In order to solve the strong kinematics coupling problem of parallel mechanisms obtained by the normal type synthesis approach, a systematic method for structural synthesis of the uncoupled spatial translational parallel mechanisms (USTPM) was presented based on the actuation wrench screw theory. Firstly, mathematic model mapping the relationship between the inputs and the outputs of USTPM was set up. Secondly, both the actuation wrench screw and actuated twist screw’s forms of the kinematical chains were obtained according to the condition that the velocity Jacobian matrix was a diagonal one. Then the rules to determine the non-actuated screws of the limbs were established in terms of the reciprocal product principle. Both criterion and steps of the limb’s type synthesis were proposed as well. Finally, the mechanisms with the expected motion characteristics were designed by selection three limbs synthesized above to connect the platform and the base. Totally 60 symmetrical USTPMs were designed. Among them, 47 mechanisms were non-overconstrained and 29 mechanisms were composed of the open single kinematic chains with idle joints. The Jacobian was a diagonal matrix of the synthesized parallel mechanisms. It was more interesting that some mechanisms’ Jacobian was the identical matrix, in which there existed one-to-one linear mapping relationship between the input velocities of the actuated joints and the output velocities of the moving platform for these mechanisms, and condition number of their Jacobians was equal to 1. So these mechanisms showed fully-isotropic throughout their whole workspace. Meanwhile, they performed very well with regard to motion and force transmission. This work contributed to enriching and improving the structural synthesis theory of the parallel mechanisms.

parallel mechanism; structural synthesis; actuation wrench screw theory; uncoupled; Jacobian matrix

10.6041/j.issn.1000-1298.2017.01.043

2016-09-17

2016-10-10

国家自然科学基金项目(50905055)、河南省高校科技创新团队支持计划项目(15IRTSTHN008)、河南科技大学重大科技项目培育基金项目(2015XTD012)和河南科技大学研究生创新基金项目(CXJJ-2016-ZR03)

张彦斌(1974—)，男，教授，博士，主要从事机构学与并联机器人理论研究，E-mail: yanbin_zh@163.com

TH112； TP242

A

1000-1298(2017)01-0325-08