基于磁导调制的直线式时栅位移传感器*
陈锡侯,曹 焕,武 亮,朱 海
(重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)
基于磁导调制的直线式时栅位移传感器*
陈锡侯*,曹 焕,武 亮,朱 海
(重庆理工大学机械检测技术与装备教育部工程研究中心,重庆 400054)
为了满足恶劣环境下精密位移测量的需求,解决现有测量方法在大量程和高精度之间无法兼顾的难题,克服小栅距造成加工难度大的缺点,提出一种基于磁导调制的驻波合成行波的新方法,研究一种新型直线式时栅位移传感器。通过对传感器测量原理的理论推导,设计了传感器的基本结构,应用三维磁场仿真软件Ansoft Maxwell对传感器进行建模与仿真,采用快速傅里叶变换(FFT)对仿真结果进行误差分析与溯源,根据分析结果对模型结构优化并进行仿真实验验证;根据优化模型制作传感器实物并搭建实验平台进行实验验证。实验结果显示:在200 mm测量范围内,测量精度达±600 nm,且传感器制造简易,成本低廉,在实际工程中具有重要的实用价值。
时栅位移传感器;高精度;大量程;磁导调制;误差特性
兼具大量程、高精度的位移测量传感器已成为精密位移测量领域重要发展需求之一[1-3]。而目前存在的测量方法二者往往无法兼顾,随着测量分辨率的提高,测量范围则受到一定局限。虽也存在极少数精密大量程位移传感器,但其对测量环境要求极高,且价格也十分昂贵。
基于扫描探针显微技术的测量方法,其分辨率虽能达0.01 nm,量程却在微米级[4-5];基于电容测微技术的测量方法,其分辨率可达0.9 nm,测量范围不超过15 mm[6];光纤位移测量方法虽也能实现纳米级分辨率,但量程也只有几个毫米[7-8];激光干涉仪虽可实现几米量程内,1 μm的精度,但其对测量环境要求极高,造价也十分昂贵[9-10]。课题组前期研制的直线式时栅位移传感器,磁场式时栅在150 mm量程内,精度仅为±32 μm[11];光场式时栅量程可达400 mm,但测量精度也仅为±2 μm,且光路复杂、对环境要求苛刻[12];电容式时栅虽能到达200 mm范围内、±300 nm的精度,但其测量信号极易受环境影响,且测量精度依赖定子精密加工[13]。
针对上述技术难题,本文提出一种基于磁导调制的直线式时栅位移传感器。测量原理基于时间量测量空间量的“时空坐标转换理论”,同时采用磁导调制形成行波的方式更易实现高精度[14];传感器结构采用前后双层,大大增强感应信号的强度,减小传感单元间涡流效应;加工工艺采用慢走丝线切割以及多层PCB制线,普通的加工方式更易实现低成本、大量程。通过理论推导,建立测量模型,通过对误差溯源优化模型,并通过实验得到验证,实现了大尺寸下的精密位移测量。
1 传感器工作原理
磁场式时栅的关键技术在于利用磁场将受位移调制的两个正交电信号耦合成测量所需的行波信号,简化模型的同时增强感应信号强度[15]。基于上述理论基础设计了基于磁导调制的直线式时栅位移传感器的结构,如图1所示。
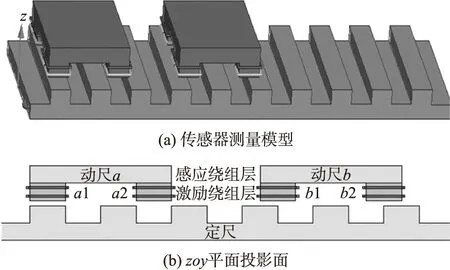
图1 传感器结构图
传感器主要分为上层定尺和下层动尺两部分,定尺上分布有等间距的齿槽结构,为简化激励绕组的结构,将其同感应绕组一样绕制在离散的动尺测头上。在动尺a上的激励线圈与动尺b上的激励线圈中分别通入正、余弦激励信号实现时间正交,动尺a与动尺b相距5 W/4实现空间正交,同时可以减少正、余弦磁路之间的相互串扰。采用前后双层结构(激励与感应绕组同层同向绕制、前后层反向绕制)以增强感应信号的强度,同时减小传感单元的涡流效应。
在动尺的移动过程中,定尺齿与动尺齿间的气隙磁导发生变化,若只考虑其恒定分量和基波分量,动尺各齿下的磁导变化规律为:
Λa1=Λ0+ΛM1cos[(2πx)/W]
(1)
(2)
(3)
(4)
式中:Λ0为磁导恒定分量;ΛM1为磁导基波分量幅值;W为极距;x为位移量。
根据电磁学理论可知,动尺上各齿的激励线圈与感应线圈的互感抗与其磁导有相同的变化规律。在动尺a激励线圈上分别通入电流ia1=Imsin(ωt),ia2=-Imsin(ωt);动尺b激励线圈上分别通入电流:ib1=-Imcos(ωt),ib2=Imcos(ωt)。则各感应线圈的输出电势分别为:

(5)
(6)
(7)
(8)
动尺a、b两部分感应线圈分别感应出两路正交的拍频驻波信号eA,eB:
(9)
(10)
再将两路驻波信号串联输出,就可以得到用于位移检测的电行波信号e。
(11)
式中:km磁场耦合系数。
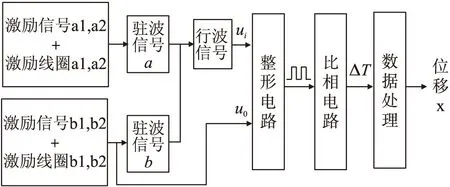
图2 测量系统工作原理示意图
将得到的行波信号与作为基准的一路激励信号整形成方波信号;送入比相电路,采用高频时钟插补技术得到两路信号之间的相位时间差ΔT;结合式(11)将时间差换算成实际的直线位移x,最后进行输出显示[16-17]。整个测量系统工作原理示意图如图2所示。
2 模型仿真与误差分析
为验证传感器原理模型的合理性及可行性,应用有限元分析软件Ansoft Maxwell对图1所示测量模型仿真分析,传感器结构参数和电气参数设置如表1所示。在时间周期为40 kHz、4 mm空间极距内,该模型仿真结果如图3所示,其中各条正弦曲线的初相角不同,代表动尺处于不同的空间位置。

表1 仿真模型参数设置
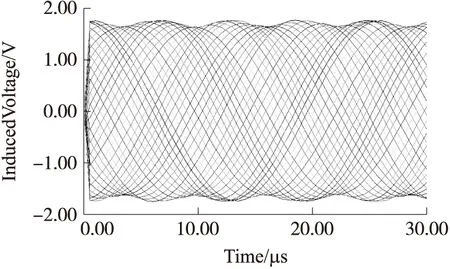
图3 模型感应线圈输出总电动势
由时栅位移传感器的测量原理可知,动尺的位移与感应电势的初相角呈线性关系,因此转子的位移是通过检测感应电势的初相角来获得。现运用快速傅里叶变化FFT(Fast Fourier Transformation),对图3中行波信号分别计算每条正弦曲线的初相角,将仿真模型中动尺的每个空间位置对应的正弦曲线初相角与设定的理论初始相角相减,便可得到测量模型中动尺在每个空间位置的初相角误差,通过转换得到相应的位移误差,如图4所示。
对测量误差数据再次进行快速傅里叶变换,得到模型中位移测量误差的谐波成分,图5是幅值谱。
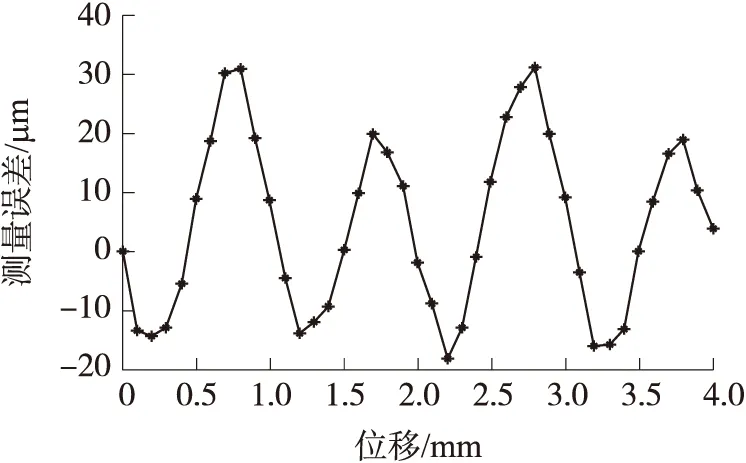
图4 动尺各空间位置的误差
由上述变换结果分析可知,仿真模型中存在较为显著的4次谐波,即主要是由结构误差引起的齿谐波。
在测量模型中,动尺齿和定尺齿均为矩形齿,随动尺相对于定尺的移动,动、定齿间的耦合系数呈现出不同值,如图6所示。传感器模型共有4对齿,随着动齿的移动,动尺a1齿、动尺b2齿、动尺a2齿、动尺b1齿依次与定尺齿出现对齐状态,耦合系数呈周期性的出现4次极大值,因此必然会造成行波信号的幅值出现一个随周期呈四次变化的误差部分。

图5 测量误差频谱图
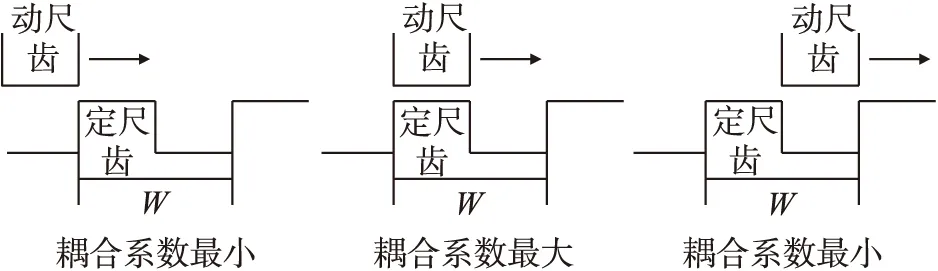
图6 动、定子齿不同位置下的耦合系数变化
3 模型结构优化
对于齿谐波的消除,目前采用的方法有斜槽法、和双层法两种,但考虑到双层法结构的复杂性,本文采用斜槽法来抑制对极内的4次谐波。斜槽法是将动尺的直槽改为有倾斜度的斜槽,从而使感应线圈接受的每相激励磁场通量的大小可以随位移均匀变化,两组感应线圈中磁通经叠加后,就形成了幅值较为平稳的电行波信号。倾斜度的大小借鉴文献[18],即将传感器单元倾斜1/4对极,使得上下端面相位相差1/8对极,即沿轴向取相同长度积分值为0,如图7所示。
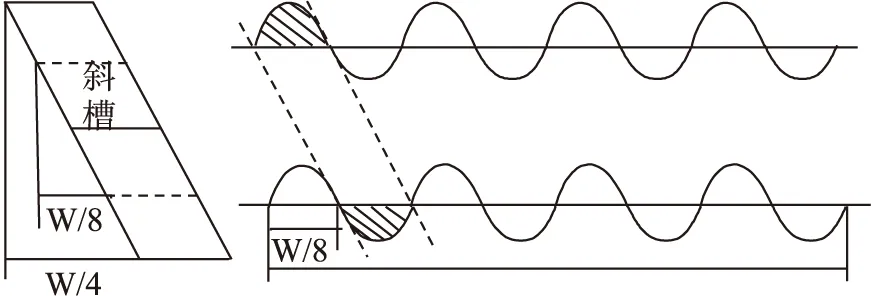
图7 斜槽法原理
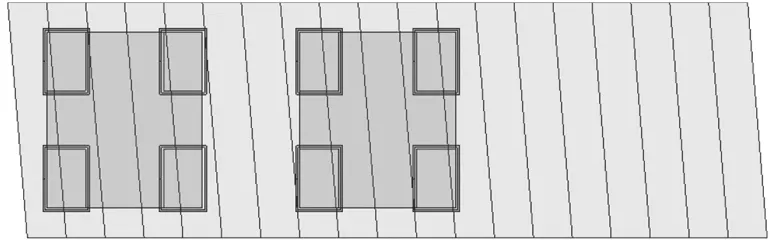
图8 改进后的传感器模型
由于传感器模型中定尺相对于动齿结构要简单的多,所以将定尺进行一定的倾斜。经过动、定尺长度比例关系换算成动尺的倾斜长度。经优化后的传感器模型如8所示。
改进后的传感器模型输出信号如图9所示,误差曲线如图10所示,模型改进后误差频谱分析如图11所示。

图9 模型改进后感应线圈输出总电动势

图10 模型改进后的测量误差

图11 模型改进后的误差频谱
由图可以看出经过模型优化后四次误差由原来的19.65 μm减弱为3.26 μm,由此可以看出采用斜槽设计能有效的提高感应信号电行波的稳定性,使信号变化曲线与理论曲线更加接近。由误差曲线可以看出模型总的误差为-1.8 μm~10.1 μm。除了微小的模型误差外,网格划分不均,划分边距较大,以及计算精度等都会给模型带来一定误差。
4 实验验证与分析
根据优化后的传感器模型,采用慢走丝线切割工艺加工传感器动尺铁芯和定尺,材料选用具有高磁导率特性的坡莫合金。为减小励磁线圈与感应线圈应绕线不均带来的误差,采用多层PCB板焊接,激励、感应线圈匝数分别为30匝、90匝。传感器实物如图12所示。

图12 传感器实物图
为验证仿真结果,搭建了以RENISHAW ML80激光干涉仪为测量基准的精密实验系统,如图13所示。将传感器定尺固定在大理石平台上;动尺与直线导轨连接,并使其与定尺保持0.3 mm的间隙,并利用驱动装置控制动尺的移动。

图13 精密实验系统
当动尺发生位移时,通过下位机实时检测时栅和激光干涉仪的数据,经处理后送与上位机输出显示。将时栅与激光干涉仪的测量值做差就得到传感器的原始误差,图14为动尺在一个空间极距内的误差分布曲线。

图14 一个极距内的测量误差
由图14可知,原始误差峰峰值约为54 μm。在实际的传感器模型中,由于正余弦激励无法实现准确正交,加工误差的存在使得正余弦感应线圈在空间上不正交,以及各层PCB板间松紧的差异造成耦合系数不同等原因都会导致两路驻波信号的幅值不等和相位不正交,从而导致电行波信号依旧存在1、2误差。由于实际模型中动、定尺齿槽的存在,依旧会存在由齿谐波引起的4次误差。
通过对上述误差进行补偿,补偿后传感器在一个极距下的精度达到了±430 nm,如图15所示。而在量程为200 mm的测量实验中,传感器精度可达到±600 nm,如图16所示。
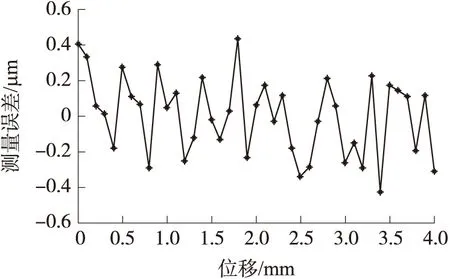
图15 补偿后一个极距内的测量误差
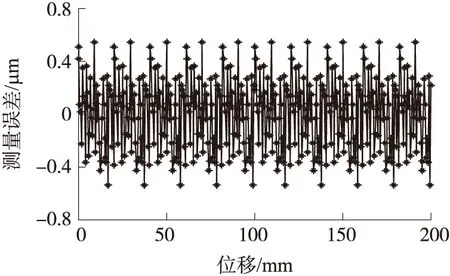
图16 补偿后200 mm内的测量误差
5 结束语
本文采用了基于磁导调制的驻波合成行波的新方法,将动尺设计成正弦尺a、余弦尺b,使两路驻波磁路分离,消除了磁路间的相互串扰,提高了传感器的测量精度;采用双排结构,增强了感应信号的强度,提高了传感器的信噪比。通过对测量系统建模与仿真,研究其误差特性,采用斜槽法对其主要误差频次进行抑制,使4次的误差由 19.65 μm减小到3.26 μm,测量系统的精度明显提高。通过对系统误差的标定,可以在大量程内实现高精度测量,具有广泛的工程实用价值。
[1] 陈本永,李达成. 纳米测量技术的挑战与机遇[J]. 仪器仪表学报,2005,26(5):547-550.
[2] 何凯,陈星,王建新,等. 高精度激光三角位移测量系统误差分析[J]. 光学与光电技术,2013,11(3):62-66.
[3] 陈自然,刘小康,郑永,等. 精密位移动态测测量信号特征辨识及细分新方法研究[J]. 仪器仪表学报,2015,36(10):2224-2230.
[4] Bykov I V.Automatized Methods for Optimization of Scanning Probe Microscope Operation[J]. Strategic Technologies,2008:179-180.
[5] Tseng A A,Notargiacomo A,Chen T P. Nanofabrication by Scanning Probe Microscope Lithography:A Review[J]. Journal of Vacuum Science and Technology B:Microelectronics and Nanometer Structures,2005,23(3):877-894.
[6] Kim M,Moon W. A New Capacitive Displacement Sensor with High Accuracy and Long-Range[J]. Sensor and Actuator A:Physical,2006,130-131:135-141.
[7] 刘义秦,谢芳,马森,等. 融合双波及单波干涉的光纤位移传感系统研究[J]. 光电子·激光,2012,23(7):1369-1373.
[8] Zhou X L,Yu Q X.Wide Range Dispacement Sensor Based on Fiber Optic Fabry-Perot Interferometer for Subnanometer Measurement[J]. IEEE Sensors Journal,2011,11(7):1602-1606.
[9] 曲兴华,王立华. 基于激光技术的亚纳米级位移测量系统的研究[J]. 仪器仪表学报,2010,31(6):1276-1281.
[10] Yoshimizu N,Lal A,Pollock C R.Nanometrology Using a Quasiperiodic Pattern Diffraction Optical Ruler[J]. Journal of Microelectromechanical Systems,2010,19(4):865-870.
[11] 黄奔,彭东林,武亮,等. 基于平面线圈的基波脉振磁场构造方法研究[J]. 传感技术学报,2015,28(10):1476-1481.
[12] 李彦,付敏,朱革,等. 基于光敏阵列直接调制的单栅式时栅位移传感器[J]. 光学精密工程,2016,24(5):1028-1035.
[13] 刘小康,彭凯,王先全,等. 纳米时栅位移传感器的理论模型与误差分析[J]. 仪器仪表学报,2014,35(5):1136-1142.
[14] 彭东林,刘小康,张兴红,等. 高精度时栅位移传感器研究[J]. 机械工程学报,2005,41(12):126-129.
[15] 武亮,陈锡侯,王阳阳,等. 磁导调制形时栅位移传感器测量方法研究[J]. 传感技术学报,2014,27(8):1043-1048.
[16] 冉扬洁,江中伟,杨继森,等. 基于TDC-GP2的高速时栅位移传感器信号处理系统的研究[J]. 传感技术学报,2014,27(12):1654-1658.
[17] 于治成,郑方燕,冯济琴,等. 纳米时栅传感器数字信号处理系统设计[J]. 传感技术学报,2013,26(11):1548-1551.
[18] 强曼君. 磁阻式多极旋转变压器[J]. 微特电机,1979(2):20-40.
Linear Time Grating Displacement Sensor Based on Permeability Modulation*
CHENXihou*,CAOHuan,WULiang,ZHUHai
(Engineering Research Center of Mechanical Testing Technology and Equipment,Ministry of Education,Chongqing University of Technology,Chongqing 400054,China)
In order to meet the demand of precise displacement measurement in the harsh environment,solve the problem that current measuring methods are difficult to balance the wide measuring range and measuring precision,and overcome the disadvantages of manufacturing difficulty due to small grating pitch,a new method,coupling two standing waves to electrical traveling wave based on permeability modulation,was proposed and a novel linear time grating displacement sensor was designed. According to the principle of sensor measurement which was derived,the basic structure of sensor was designed. The 3D magnetic field simulation software Ansoft Maxwell is adopted to build a simulation model of the sensor. Using fast Fourier transform(FFT)to analyze the error of simulation results and trace to the source. According to the analysis results,the model structure was optimized and the simulation results are verified.According to the optimization model,The sensor was manufactured and the experimental platform was built to verify the experimental results. The experiment results show that the measurement accuracy reaches 600 nm in the range of 200 mm. The sensor produces easily and cost low,which has important practical value in practical engineering.
time-grating displacement sensor;high precision measurement;long range;permeability modulation;error characteristic

项目来源:国家自然科学基金项目(51675071,51405049);重庆市科技研发基地能力提升计划(cstc2014pt-sy40002)
2016-09-08 修改日期:2016-12-09
TH711
A
1004-1699(2017)01-0026-05
C:7230
10.3969/j.issn.1004-1699.2017.01.005

