低g值微惯性开关中阿基米德平面螺旋梁的设计*

张凤田,熊 壮,金伟锋,唐 彬

(中国工程物理研究院电子工程研究所,四川 绵阳 621900)

低g值微惯性开关中阿基米德平面螺旋梁的设计*

张凤田*,熊 壮,金伟锋,唐 彬

(中国工程物理研究院电子工程研究所,四川 绵阳 621900)

针对低g值微惯性开关对微弹簧的系统刚度达到(0.1～10)N/m数量级的要求,设计了一种阿基米德平面螺旋梁结构的微惯性开关。根据材料力学中的卡氏定理和线弹性理论,推导了阿基米德平面螺旋梁的弹性系数计算公式,并与ANSYS有限元仿真分析结果进行了对比。基于推导的弹性系数计算公式设计了一种三根阿基米德平面螺旋梁支撑的动作阈值5.5gn的微惯性开关,并采用SOI硅片以及玻璃-硅-玻璃键合技术进行了加工,在离心转台上对开关实际动作阈值进行测试,并将测试值与设计值进行对比。结果表明,采用推导到的阿基米德平面螺旋梁弹性系数计算公式计算结果与ANSYS仿真结果相近,基于推导的弹性系数计算公式设计的三根阿基米德平面螺旋梁支撑的微惯性开关动作阈值设计值与实测值相近,单根阿基米德平面螺旋梁弹性系数约0.8 N/m,能够满足低g值微惯性开关低刚度的要求,推导的弹性系数计算公式能够用于基于阿基米德平面螺旋梁的低g值微惯性开关的设计。

微惯性开关;阿基米德;卡氏定理;平面螺旋梁;微弹簧

低g值惯性开关广泛运用在汽车安全气囊、工业安全控制和航空航天等领域[1]。传统的低g值惯性开关通常采用精密机加的方式加工质量块和绕制弹簧,再进行装配、调试、筛选,对于几十到几百g的惯性开关生产相对比较容易,但是当开关的动作阈值要求小于10gn时,传统精密机加的惯性开关不仅体积大、成本高,而且装调非常困难。随着微机械加工技术的发展,与微加速度传感器相比具有抗干扰能力强、工作可靠、运用简单等优点的微惯性开关已成为国内外微纳技术领域的一个重要研究方向[2-3]。目前报导的大部分微惯性开关的闭合阈值均大于10gn,主要应用于冲击环境条件下敏感冲击加速度[4～10],关于敏感准静态、小于10gn加速度信号的低g值微惯性开关的文献报道相对较少。

为了敏感10gn以内的准静态加速度,可以增大微惯性开关质量块质量、减小质量块行程、减小开关中微弹簧刚度。由于MEMS技术的微型化,质量块最大只能达到毫克数量级,所以增加质量块措施有限;减小质量块行程采用MEMS加工技术容易实现,但是对于低g值惯性开关,过小的质量块行程会使得惯性开关在一般的振动冲击下就会动作,引起开关误动,所以低g值微惯性开关通常需要减小惯性开关中微弹簧刚度,使得微弹簧弹性系数达到(0.1～10)N/m数量级,从而降低惯性开关的“弹簧-质量”结构的固有频率,实现微结构本身“机械滤波”,减小冲击或振动产生的各种频率干扰信号的影响。陈光焱等人[11]采用UV-LIGA工艺研制的基于阿基米德螺旋梁的微惯性开关,由于只采用了一根螺旋梁,开关接触实质为线接触,不利于开关导通电阻的降低,并且文中没有对螺旋梁弹性系数进行分析。王超等人[12]采用体硅工艺研制的低g值微惯性开关采用了两根结构简单、加工容易实现的平面矩形螺旋线型低刚度微弹簧,微弹簧弹性系数只有0.55 N/m。本文在文献[11-12]基础上,采用SOI硅片作为结构材料,结合玻璃-硅-玻璃键合技术,设计了一种由三根阿基米德平面螺旋梁支撑的低g值微惯性开关,推导了阿基米德螺旋梁的弹性系数,并针对具体结构将理论计算结果与ANSYS仿真结果、样品实测结果进行了对比。

1 原理与设计

基于阿基米德平面螺旋梁的低g值微惯性开关采用双触点结构,如图1所示,由玻璃盖板、SOI结构和玻璃基底三部分组成。SOI结构为惯性敏感单元,是整个结构的核心部件,即“弹簧-质量”结构,包括悬空的感知惯性加速度的圆柱形质量块和三根结构完全相同的阿基米德平面螺旋梁,圆柱形质量块通过三根阿基米德平面螺旋梁支撑悬空,质量块底面制备金属电桥。带有浅槽的玻璃盖板用于限制质量块的反向运动,同时在划片和后续测试中保护“弹簧-质量”结构。玻璃基底上有凹槽,并在凹槽上加工接触凸点,凸点上制备金属电极将开关接触触点信号引出。考虑结构的加工工艺性,通过增加阿基米德平面螺旋梁圈数即梁的等效长度,可以调整阿基米德平面螺旋梁在开关敏感方向上的刚度。阿基米德平面螺旋梁在微惯性开关敏感方向(即OZ向)厚度较薄,刚度较小,而在OXY平面内刚度较大对OXY平面内加速度信号响应较小,有利于降低非敏感方向加速度信号对微惯性开关工作可靠性的影响。

图1 低g值微惯性开关结构示意图

基于螺旋梁的低g值微惯性开关是典型的“弹簧-质量-阻尼”系统,其运动规律满足牛顿第二定律。在OZ方向上惯性加速度a(t)的作用下,惯性开关的力学平衡方程可以表示[13]为:

(1)

式中:z(t)为质量块相对基底的运动位移;ξ为系统阻尼比;Ω=2πf为“弹簧-质量”结构固有角频率;k、m、β分别为系统的等效刚度、等效质量和阻尼系数。微惯性开关的工作原理为:在惯性加速度作用下,可动质量块向固定基底运动,当加速度达到闭合阈值时,质量块底面上的金属电桥与基底接触触点上的金属电极同时接触,开关提供导通电阻信号。由于低g值惯性开关敏感的惯性加速度信号是准静态的,采用准静态分析方法[14],忽略式(1)中的导数项,惯性开关的闭合阈值ath可以表示为:

(2)

式中:Z0为质量块和金属电极间的初始间距。若实测惯性开关动作阈值ath,由质量块质量m以及质量块与金属电极间的初始间距Z0,也可由下式反算出图1所示微惯性开关中单根阿基米德螺旋梁的弹性系数:

(3)

式中:ρ为硅质量块的密度,R为质量块半径,Hm为质量块厚度。

2 理论分析

在一定的设计条件下,所研究的阿基米德平面螺旋梁的变形在线弹性范围之内,因而可以运用材料力学中的卡氏定理求得螺旋梁在力作用点的线性位移,进而根据线弹性理论得到螺旋梁的弹性系数。

由于质量块厚度相对较大,可将其看作为一个不发生形变的刚体。螺旋微弹簧厚度只有几十微米,而质量块厚度达到几百微米,忽略螺旋梁本身质量影响。根据图1惯性开关原理图,可以假设质量块惯性力P垂直于XY平面,作用于质量块质心o点,取螺旋梁上微元体dl,由于P始终与螺旋梁横截面在同一平面,所以螺旋梁微元体只受扭转作用,如图2所示。螺旋梁类似细长梁,其剪切应变能可以忽略不计。基于均匀、连续且各向同性材料的假设,根据卡氏定理[13],阿基米德平面螺旋梁沿力P作用方向上的位移δ可以表示为:

(4)

式中:Gt为剪切模量;It为抗扭刚度;阿基米德平面螺旋梁的扭矩T:T(θ)=P×rz(θ);螺旋梁中心线rz表达式为:rz=rz0+a×θ,rz0为螺旋梁中心线初始半径,a为径向递增系数;θ1为螺旋梁中心线初始角度、θ2为螺旋梁中心线终止角度。

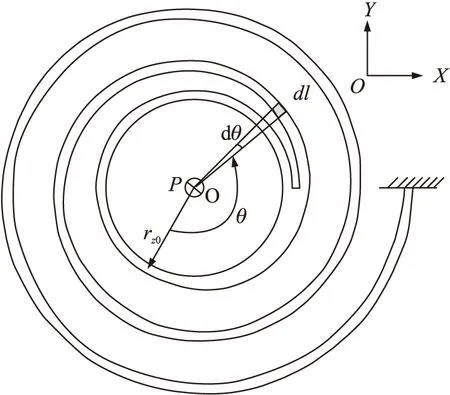
图2 单根阿基米德螺旋微弹簧结构示意图

将相关参数代入可以得到:

(5)

单根阿基米德平面螺旋梁弹性系数为:

(6)

式中:抗扭刚度It=βHbW3,β是与梁矩形截面边长比W/Hb有关的系数,可通过查表[13]得到。G=E/2(1+v)为剪切模量,E、v分别为螺旋梁结构材料(体硅)的杨氏模量和泊松比,E=166GPa,v=0.22。

本文设计的阿基米德平面螺旋梁中心线初始半径rz0为1 082.5μm;梁宽W为135μm,梁厚Hb为30μm;螺旋梁的径向递增参数a为83.6×10-6;螺旋梁初始角度θ1为2.1,螺旋梁终止角度为14.65。由式(6)可以计算单根阿基米德平面螺旋梁弹性系数kp=0.832N/m。

3 仿真计算

基于前面设计的阿基米德平面螺旋梁结构尺寸,设计了半径R为1 080μm、厚度t为570μm的质量块,三根阿基米德平面螺旋梁支撑的微惯性开关,利用ANSYS软件对微惯性开关进行了有限元仿真分析。三根阿基米德平面螺旋梁端面连接的硅框固支,给质量块施加惯性加速度am=5.5 gn,计算微惯性开关在敏感方向的最大位移Zmax。

图3是ANSYS静力学仿真计算得到的Z方向位移分布云图,可以看出给质量块施加5.5 gn惯性加速度后,微惯性开关敏感方向质量块发生最大位移Zmax为108.5μm,将质量块的尺寸参数R、Hm以及硅材料密度ρ代入(3)式可以得到单根阿基米德平面螺旋梁的弹性系数kp=0.805N/m。

图3 ANSYS仿真计算结果

4 实验测试

采用多层对称SOI硅片,即Si(270μm)-SiO2(0.7μm)-Si(30μm)-SiO2(0.7μm)-Si(270μm),以及玻璃-硅-玻璃键合技术,根据(2)式以及前面阿基米德平面螺旋梁的结构尺寸,设计加工了动作阈值5.5 gn、三根螺旋梁支撑的微惯性开关,开关运动间隙Z0为110μm。微惯性开关的加工工艺流程如下:①在SOI硅片上光刻,采用lift-off工艺制备Cr/Au/Pt金属电桥,如图4(a)所示;②双面光刻SOI硅片,双面ICP刻蚀硅至SiO2层,形成微惯性开关质量块,如图4(b)所示;③光刻SOI硅片,湿法腐蚀SiO2薄膜至SOI片中间硅层,如图4(c)所示;④ICP刻蚀透SOI片中间硅层,如图4(d)所示;⑤光刻玻璃盖板,湿法腐蚀玻璃形成玻璃盖板上质量块运动间隙,如图4(e)所示;⑥光刻玻璃基底,湿法腐蚀玻璃形成玻璃凹槽,形成微惯性开关的运动间隙Z0,如图4(f)所示;⑦光刻玻璃基底,湿法腐蚀玻璃在玻璃基底凹槽内形成接触凸点,如图4(g);⑧光刻玻璃基底,采用lift-off技术在玻璃凹槽上形成微惯性开关的金属电极,如图4(h)所示;⑨将SOI片与玻璃盖板、玻璃基底三者静电键合在一起,如图4(i)所示;⑩采用多次划片技术露出玻璃基底凹槽内的开关接触电极。

图4 微惯性开关芯片制备流程

图5 微惯性开关硅结构扫描电镜图

采用图4微惯性芯片制备流程加工的微惯性开关SOI结构样品扫描电镜图如图5所示。实测微惯性开关圆柱形质量块半径R为1 070μm,玻璃基底键合表面到接触凸点间隙Z0为110μm。将微惯性开关样品装在离心机上进行测试,测试曲线如图6所示。

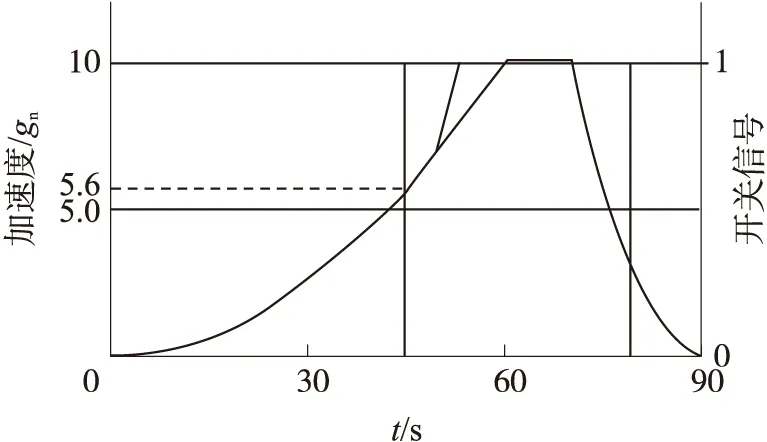
图6 微惯性开关动作实测曲线

从图6可见,开关动作阈值实测结果为5.6 gn,将实测的质量块半径R、Z0代入(3)式可以反算单根阿基米德平面螺旋梁的弹性系数为0.794N/m。

5 结论

本文采用卡氏定理推导了用于低g值微惯性开关中阿基米德平面螺旋梁在开关敏感方向上的弹性系数,用ANSYS对微惯性开关进行了静力学有限元分析并计算出阿基米德平面螺旋梁的弹性系数,最后采用SOI硅片以及玻璃-硅-玻璃多层键合工艺制备了三根阿基米德平面螺旋梁支撑的微惯性开关,基于离心机上开关动作阈值的测试结果以及开关结构尺寸实测结果,反算了单根阿基米德螺旋梁在开关敏感方向的弹性系数,3种方式得到的阿基米德平面螺旋梁弹性系数相差较小。所以,本文推导的阿基米德平面螺旋梁弹性系数可以用于指导微惯性开关中阿基米德平面螺旋梁的设计。

致谢

感谢中国工程物理研究院电子工程研究所传感器与执行器研究中心MEMS工艺组同志在加工工艺方面给予的支持。

[1] 陈光焱,王超. 微惯性开关设计技术综述[J]. 信息与电子工程,2009,7(5):439-442.

[2] 郑长勇,陈军宁. 一种新型MEMS 加速度计温度补偿方法研究[J]. 传感技术学报,2015,25(1):39-42.

[3] 高阳,李庆丰,陈艳,等. 飞行器用高精度小量程石英微加速度计研究[J]. 传感技术学报,2015,28(6):792-797.

[4] Tadao Matsunaga,Masayoshi Esashi. Acceleration Switch with Extended Holding Time Using Squeeze Film Effect for Side Airbag Systems[J]. Sensors and Actuators A,2002,100(1):10-17.

[5] Yang Zhuoqing,Ding Guifu,Chen Weiqiang,et al. Design,Simulation and Characterization of an Inertia Micro-Switch Fabricated by Non-Silicon Surface Micromachining[J]. J Micromech Microeng,2007,17:1598-1604.

[6] Zhao Jian,Jia Jianyuan,Zhang Wenbo,et al. Nonlinear Dynamic Characteristics Analysis and Design of a MEMS Inertial Sensing Device[J]. Nanotechnology and Precision Engineering,2006,4(4):70-75.

[7] 陈光焱,杨黎明. 一种高g值微冲击开关的研制[J]. 爆炸与冲击,2007,27(2):190-192.

[8] Wang Y,Yang Z,Xu Q,et al. Design,Simulation and Characteriza-tion of a MEMS Inertia Switch with Flexible CNTs/Cu Composite Array Layer between Electrodes for Prolonging Contact Time[J]. Journal of Micromechanics and Microengineering,2015,25(8).

[9] Chen W,Wang Y,Cheng P,et al. Fabrication of a Novel Contact-Enhanced Horizontal Sensitive Inertial Micro-Switch with Electroplating Nickel[J]. Microelectronic Engineering,2014,127(13):21-27.

[10] Liu H B,Dai L H,Kang X G. Ballistic Characteristics of Non-Silicon MEMS Inertia Switch[J]. Science Technology and Engineering,2011,411:452-455.

[11] 陈光焱,吴嘉丽,赵龙,等. 基于阿基米德螺旋线的低g值微惯性开关[J]. 光学精密工程,2009,17(6):1257-1261.

[12] 王超,陈光焱, ,等. 基于MEMS技术的低g值微惯性开关的设计与制作[J]. 传感器技术学报,2011,24(5):653-657.

[13] 单辉祖. 材料力学[M]. 北京:高等教育出版社,2010.

[14] Cho Y H,Go J S,Kwak B M,et al. Snapping Microswitches with Adjustable Acceleration Threhold[J]. Sensors and Actuators A,1996,54(1-3):579-583.

Design of Archimdes Planar Micro-Springs Used in Low-gMicro Inertia Switch**

ZHANGFengtian*,XIONGZhuang,JINWeifeng,TANGBin

(Institute of Electronic Engineering,China Academy of Engineering Physics,Mianyang Sichuan 621900,China)

Aimed at the micro-spring with stiffness down to(0.1～10)N/m magnitude in low-gmicro inertia switch,a planar micro-spring based on the Archimdes planar helical spring is designed. The elastic coefficient formula is derived with the Castigliano’s theory and the linear elasticity theory of material mechanics,and compared with the ANSYS finite element method simulation results. A micro inertia switch with acceleration threshold of 5.5gnsupported with three Archimdes planar micro-springs is designed and fabricated based on SOI wafer and anodic bonding of glass-silicon-glass. Acceleration threshold of the fabricated micro inertia switch is measured with a centrifuge and compared with the designed value. The theoretically calculated results using the derived elastic coefficient formula agree well with the ANSYS simulation results,and acceleration threshold of the designed inertia switch agrees with the measurement results. The elastic coefficient of the designed and fabricated Archimdes planar helical spring is about 0.8 N/m. It conforms to the low stiffness requirement of low-gmicro inertia switch. The derived elastic coefficient formula can be used in the design of low-gmicro inertia switch with Archimdes planar helical springs.

micro inertia switch;Archimdes;Castigliano’s theorem;planar helical spring;micro spring

张凤田(1976-)男,重庆万州人,副研究员,2007年于大连理工大学电信学院获博士学位,现主要从事MEMS惯性器件的设计和加工技术研究,zhangft114@163.com。

项目来源:中国工程物理研究院科学技术发展基金项目(2012A0403018)

2016-04-05 修改日期:2016-06-16

TP212;TH135

A

1004-1699(2017)01-0039-05

C:11819;11397

10.3969/j.issn.1004-1699.2017.01.008