“轴对称”教学纪实与评析
张文静 李伟荣

教学内容:人教版小学数学四年级下册P82。
教学目标:
1.通过看一看、数一数的活动,进一步认识轴对称图形和对称轴,探索轴对称图形的对称点与对称轴之间的关系。
2.通过观察、操作等活动,能在方格纸上补全一个轴对称图形。
3.让学生在探索的过程中进一步增强动手操作能力,发展空间观念,培养审美观念和学习数学的兴趣。
教学重点:探索轴对称图形的对称点与对称轴之间的关系。掌握补全轴对称图形的方法。
教学难点:探索对称图形对应点特点,能准确地在方格纸上画出轴对称图形的另一半。
教学流程:
一、课前交流,激发兴趣
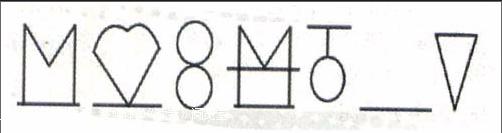
师:同学们,课前我们来做个数学游戏。它曾经是美国哈佛大学的测试题(出示题)。同学们仔细观察,前几幅图有什么特点?
生:我发现它们都是对称的。
师:那么在空白处我们接下来应该填什么样的图形呢?
生:填一个正6和一个反6。因为前面几个图形是正1和反1,正2和反2……所以空白处应该是正6和反6。
师:你很善于观察,发现了图形对称的规律,现在我们开始今天的学习。
二、复习导入。回顾旧知
师:我们在二年级的时候学习过轴对称图形,请大家回忆一下什么是轴对称图形,并举个生活中的例子。
生:把一个图形沿着一条直线对折,两边完全重合,这样的图形就是轴对称图形。比如黑板的形状是轴对称图形。比如课桌的形状是对称的。(学生举例。)
师:生活中有很多物体的形状是轴对称图形,那么这节课我们就在原来的基础上,深入地研究轴对称图形。(板书课题:轴对称。)
三、实践反思。探究新知
1.学画轴对称图形的对称轴。
师:这些是生活中常见的轴对称图形,接下来请你们尝试着画出它们的对称轴。
(学生订正。)
师:现在我们隐去它们的颜色和图案,再来看看,这些图形又有几条对称轴?(课件:由图案过渡到图形。)
师:由此看来,有的图形只有一条对称轴,而有的图形不只一条对称轴。
2.探究轴对称图形的性质。
师:通过你的感觉来判断,它是不是轴对称图形?你是怎么知道的?
生:沿着对称轴对折、两边完全重合。
师:真善于运用。你是利用已有的轴对称图形的概念来进行判断。在轴对称图形中,有很多像A和A这样的点,给它们取个名字,你想叫什么呢?
生:对称点。
师:为什么?
生:因为在这个轴对称图形中,点A和点A沿对称轴对折后,能够完全重合。
师:是这样吗?老师将屏幕上的图形按比例缩小了。(在半透明纸上用红笔标出这两个点,沿对称轴对折。)同学们看,这两个点怎么样了?两边的图形呢?
生:重合了。
师:由此证明,刚才同学们的想象、猜测是正确的。就像同学们说的那样,数学上把对称图形中沿对称轴对折,能够完全重合的点叫对应点。下面我们就从轴对称图形中最基本的对应点入手做进一步的研究。
师:在研究图形与几何的时候经常会用到格子图,它便于我们观察和研究。我们把小松树放到格子图中,研究一下对应点有什么特点。
师:拿出你的格子图,你能尝试着找出几个小松树的对应点吗?想一想你可以怎样找,再数一数、画一画,观察这些对应点有什么共同的特点,把你的发现在小组中说一说。(出示学习要求,学生自主探索,小组交流。)
生1:我是用对折的方法找到点B的对应点B的。
生2:我找的点B、点B和他的位置不同,方法也不一样。我是用数格子的方法找到点B和它的对应点B的。我是这样找的:先确定了点B,从点B向右数了2个格子就到了对称轴;再从对称轴开始向右再数2个格子,就找到了B。
生3:我也用数格子的方法找的。我先从点C向右数了1个格子到了对称轴;我又从点C开始向左数了1个格子也到了对称轴。还对折验证了一下。
师:为同学们点赞,你们不仅表达流利,还很严谨。同学们找到了这么多对应点,观察一下这些对应点,你有什么发现?
生:A点到对称轴的距离是3小格,A。点到对称轴的距离也是3小格,对应点到对称轴的格子数量是相等的,我发现对应的两个点到对称轴的距离是相等的。
师:他是抓住了两点到对称轴的格子数量来研究发现的,谁的发现也是这样的?(进行有效反馈。)还有别的发现吗?
生:把对应点连起来,我发现这些连线都跟对称轴垂直。
师:是这样吗?大家看看屏幕。(对应点连线,借助格子图感知。)的确,对应点连线垂直于对称轴。对应点到对称轴的距离就是指从对应点到对称轴的垂线段长度。
师:就像同学们发现的那样,当A与A点到对称轴的距离相等,同时,它们的连线与对称轴互相垂直,我们就说A与A点是这个对称图形的一组对称点。你还能找到其他对称点吗?(学生进行汇报。)
师:刚才同学们找到了很多组对称点,也就是说任意一点都可以找到它的对称点。那么由这些密密麻麻的对应点所连成的线段呢?
生1:由对应点连成的线段也是对应的。
生2:在对称图形中,对应点是对称的,它们所连成的对应线段也是对称的。
师:研究对称图形的对应线段时,不仅要考虑到长度,还要注意形状。我们再来看,由这些线段所围成的图形呢?
生:都是轴对称图形。
师:你们由对称点想到了线段,由对称线段想到了对称图形。你们太了不起了!现在就拿起这个图形,我们再次感受一下这些点、线、形沿对称轴对折完全重合。(课件演示。)
师:我们借助于方格图,通过寻找对称点,再由点到线、到形,层层深入,共同去思考、去推理、去证明,总结发现了轴对称图形的特点是:对称点到对称轴的距离相等。(板书。)
3.补全轴对称图形。
师:同学们不仅发现了轴对称图形的这个特点,而且在这个过程中还掌握了一种科学严谨的数学研究方法。接下来,我们就用轴对称图形的这个特点来解决一个实际问题。(课件出示例2。)想象一下,完整的这个图形应该是什么样呢?
生:是个五角星。
师:你能把这个轴对称图形补全吗?大家动手试一试。(生展示交流。)
师:你们怎么画得又快又好?
生:我是先画出这些点的对称点,最后把它们连起来。
师:你们在画的时候,其实都是先找到这几个点,为什么就单单找了几个对应点呢?
生:这些对应点都在端点,找准了,就可以画得又快又准了。
师:对呀,它们是这个图形的关键点。找到关键点,定准了它们的对应点,最后就可以连点成形了。(板书:找关键点——定对称点——连点成形。)
四、灵活应用,拓展延伸
师:通过动手实践,你们归纳出了补全轴对称图形的好方法,下面就应用这个好方法,我们再来画一画。(学生完成数学书P84做一做2,展示交流画法。)
师:看来,同学们已经掌握了补全轴对称图形的方法。下面给你们来一个挑战,你能画出这条弧线的对称图形吗?
生:能。
师:谁到前面指一指?(生指画。)
师:看,是这样吗?(课件出示。)再看,我们换一条对称轴,它们两个的对称图形在哪儿呢?(生指画。)
师:对吗?再变,它的对称图形在哪儿呢?你来指一指,注意看他的手势。(生指画。)师:老师把它进行了装饰。
师:正是因为生活中有很多的轴对称现象,才将我们的生活装扮得更加美丽,老师就把这些花朵送给你们,希望你们就像美丽的鲜花一样在阳光下茁壮成长。
评析:
张老师的这节课依托学生的认知经验,以精巧的数学活动为载体,促进了学生对轴对称图形的性质、特征及其应用的自主建构,体现了学生的数学学习过程是生动的、主动的、富有个性的过程。在学生去经历、去发现、去再创造的活动过程中,教师因学活教,顺学而导,突出了对学生空间观念这一数学核心素养的培养。
一、关注已有经验,在唤醒中发展空间观念
这节“轴对称”是教材改版后新增的教学内容,是二年级学习的简单轴对称知识的延伸
张老师充分挖掘教材资源,通过课前挑战哈佛大学的测试题,唤醒学生对学习过的轴对称图形的认知,激发学生的学习兴趣,教师深知数学概念的掌握要建立在生活经验和认知经验的基础上。教师借助学生的生活经验,通过观察、书空画轴感知生活中的对称现象,而后舍弃各个实物图中非几何属性的因素,抽象出平面图形,进而完成画对称轴的自主学习,这样的设计能体现将生活经验提炼为数学概念的过程,突出本节课研究的对象是图形,在激活经验中发展了学生的空间观念。
二、关注探究体验,在建构中发展空间观念
为了深化学生对轴对称图形特征的认识和理解,教师设计了折一折、找一找、画一画、连一连等层层深入的探究体验活动,使学生经历“感知对称——探究对称——理解对称”的过程,知识建构层层深入,教师教学重点找得准、落得实,策略有效。例1的教学是本节课的重点教师引导学生在“怎样判断一个图形是否是轴对称图形”问题的思考下,自主进行方法的迁移,利用对折,发现点重合,引出对称点的教学。再让学生从图中寻找到更多组对称点,学生在多维的找对称点的方法的碰撞交流中,感知对称点的连线与对称轴互相垂直,在明晰对称点到对称轴距离概念的基础上,探究得到“对称点到对称轴距离相等”这一重要性质特征,并进行了有效升华。教师引导学生进一步探究发现,对称图形上每一个点都可以找到它的对应点,这些点的连线是对称线段,由对称线段围成的图形是对称图形。这样由点到线、到形,层层深入,加深学生对于轴对称图形特点的认识,并且利用在头脑中想象图形沿着对称轴对折,两部分完全重合的过程,培养了学生空间距离感和方位感,以此提升学生的空间观念
三、关注迁移拓展,在应用中发展空间观念
轴对称是“图形与几何”领域中图形与转换中的重要内容,发展学生的空间观念也是本节课的一个重要目标张老师不仅在新知的建构中发展学生的空间观念,更注重学生在知识的迁移和应用中发展空间观念.首先,教师在补全对称图形的知识应用中发展了学生的空间观念,抓住关键对应点进行画法的优化。其次,借助做一做中的基础题目,有效地落实了知识目标。最后,教师进行了思维层次更高的空间想象能力的引领和培养一教师引导学生一边想象,一边书空画出一段弧线的以竖直方向为对称轴的轴对称图形,一组弧线,两组弧线以左、右倾斜45°不同方向为对称轴的轴对称图形,最终形成了美丽的花朵,引发学生对对称美的关注和感知,把对学生空间观念素养的培养推向高潮。前一次任务的顺利完成恰恰是下一次挑战性任务的开始,使学生的空间观念在不断的思维挑战中得到发展和升华。
编辑/宋宇

