一种基于历史监测数据的谐波污染主特征群筛选方法

林坤杰潘 夏张 嫣邵振国

（1.福州大学电气工程与自动化学院，福州 350116；2.国网福建省电力有限公司宁德供电公司，福建 宁德 352000）

一种基于历史监测数据的谐波污染主特征群筛选方法

林坤杰1潘 夏2张 嫣1邵振国1

（1.福州大学电气工程与自动化学院，福州 350116；2.国网福建省电力有限公司宁德供电公司，福建 宁德 352000）

对谐波污染用户的耦合模型需要考虑不同次数谐波之间的相互影响，这将使得模型非常复杂，从而无法基于在线监测辨识模型参数建模。本文提出一种基于历史监测数据的谐波主特征量筛选方法，首先利用统计分析中常用的主成分分析（principle component analysis,PCA)方法，通过主成分和原始变量之间的相关系数计算谐波特征群指标；然后根据该指标历史监测数据中提取能够用于谐波分析的谐波污染主特征群；最后，以宁德市配电网采集的电能质量监测数据为例进行分析，验证所提出方法的可行性。

谐波；主特征群；主成分分析；电能质量监测

近年来，大量电力电子装置等非线性负荷的并网运行使得电力系统中的谐波污染越来越严重。电能质量恶化问题已经引起电网管理部门的关注，通过实时监测评估电能质量并采取相应的治理措施已成为保证电网安全、经济运行的重要措施[1]。建立一种适当的模型来表征谐波污染用户的运行特性，可以分析用户对电网谐波分布的影响，并实现优化治理[2]。国内外学者在谐波建模的研究上作了许多有效的工作，取得了一定成果[3-7]。还有学者通过求取概率密度函数来近似获取谐波污染用户对.电网的污染程度[8-9]。

电能质量在线监测网提供了电力系统中最全面完整的谐波检测数据[10]，是谐波污染用户建模的最直接数据源。但谐波用户耦合模型考虑了不同次数谐波的相互影响，使得模型非常复杂而无法实现参数辨识[11]。因此，工程上需要从大量历史监测数据中确定谐波主特征群，以便针对谐波主特征群建立工程实用模型。

现有对于谐波主特征次数的判断基本上是根据系统非线性负荷的运行特性得到的。一般来说，电网中3、5、7、11等次数的谐波含量较大[12]。但是，当同一个监测点中存在多种不同特性的负荷时，仅根据单个负荷的运行特性无法判断监测点的谐波主特征次数，需要通过监测数据分析得出结论。

本文提出一种基于在线历史数据的谐波主特征量筛选方法，在测点用户非线性负荷特性未知的情况下，利用统计分析中常用的主成分分析方法，通过相关系数计算谐波特征群指标，根据该指标从在线监测数据中提取能够用于谐波分析的主特征群。之后，以宁德市配电网的电能质量监测数据为例进行分析，验证所提出方法的可行性。

1 主成分分析

1.1 基本思想及求解过程

主成分分析的思路是用若干互不相关的综合变量来代替原来众多的变量，并使这些综合变量尽可能多地包含原来的变量信息[13]。

设某一研究对象具有p个指标，分别用X1、X2，…、Xp表示，这p个指标构成了p维随机向X= [X1，X2，…，Xp]T，其均值为μ，协方差矩阵为Σ。

对X进行线性变换后的综合变量为Y，如式（1）所示。

要使Yi尽可能大且各Yi之间互相独立，且Yi的方差不能任意增大，常用的线性变换约束是：

1）γi(γi)T=1(i=1，2，…，p），其中γi=(γ1i，γ2i，…，γpi)T。

2）Yi与Yj相互无关（i≠j，i，j=1，2，…，p）。

3）Y1，Y2，…，Yp的方差依次递减。

基于以上3条约束所确定的综合变量Y1、Y2，…，Yp分别被称为原始变量的第一、第二至第p个主成分。

实际上，求解主成分一般从协方差矩阵或相关矩阵的结构分析入手，而相关矩阵又是将原始变量标准化后的协方差矩阵。结合主成分基本理论可知，求X的主成分等价于求它的协方差矩阵的所有特征值及相应的正交单位化特征向量。假设对X的协方差矩阵Σ进行特征值分解后，其特征根为λ1、λ2、…，λp（λ1≥λ2≥…≥λp），对应特征向量为γ1、γ2、…、γp，则按特征值由大到小所对应的正交单位化特征向量为组合系数的X1、X2、…、Xp的线性组合分别为X的第一、第二到第p个主成分，如式（1）所示。而各主成分的方差等于相应的特征值。

用ωm表示前m（m＜p）个主成分包含信息的程度，即前m个主成分的方差占所有主成分方差和的比值，称为方差的累计贡献率，如式（2）所示。

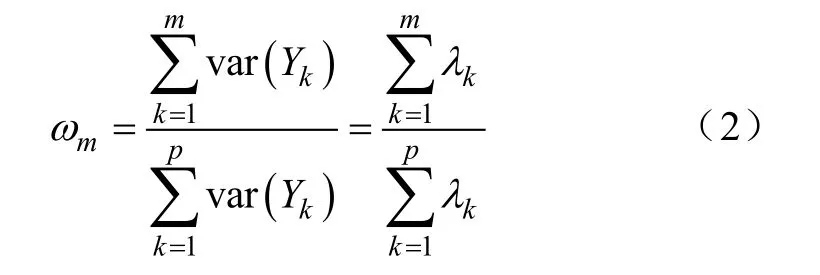
式中，var(Yk)表示Yk的方差。根据ωm大小选取合适数量的主成分，使得在简化问题的同时又能够做到尽可能多地保留原数据的信息。通常，所取m应使得累积贡献率ωm达到80%以上为宜。

除了求出主成分分量外，主成分分析还可以求取第k个主成分Yk与原始变量Xi之间的相关系数ρ(Yk,Xi)称为因子负荷量，如式（3）所示。

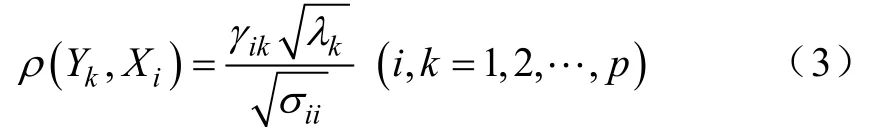
式中，σii为原始变量Xi的方差；γik是特征向量γk的第i个分量，λ1为对应特征向量γk的特征根。

1.2 监测数据预处理

由 1.1中可知，求解主成分的过程实际上是对协方差矩阵或相关矩阵进行分析，两者在求解过程上是一致的，但通过这两种方式求取的主成分结果往往差别很大，这主要是因为标准化数据会抹杀原始变量的离散程度差异。一般而言，对于度量单位不同或取值范围彼此差异非常大的指标，考虑将数据标准化后求解协方差矩阵进行分析；而对同度量或取值范围在同数量级的数据，还是直接从协方差矩阵求解主成分为宜[13]。本文所研究的数据变量为各次谐波的同一种统计数据，变量之间的量纲相同且取值范围差别不大，因此，本文考虑不对数据进行标准化处理，以保留数据的离散程度信息。

根据GB/T 14549—1993《电能质量公用电网谐波》的规定，不同次数的谐波电流其限值有很大的差别。为了结合国标对谐波进行分析，考虑在主成分分析前对电能质量监测系统获得的谐波数据，可利用式（4）对各次电流对应限值进行标幺化。

在对监测数据进行标幺化后，可以在保存谐波电流离散程度差异的前提下，使数据无量纲化，使分析更加合理。

2 谐波主特征群筛选

在谐波用户的建模中，大量的在线监测信息有助于谐波污染用户建模，但完备的谐波模型包含相互影响的谐波电压和电流状态量，这使得模型非常复杂而无法实现参数辨识。如果能通过主成分分析，用较少的映射来尽可能多的描述原始数据的信息，就可以使建模问题简单化。

在线监测系统存储的是一个量测周期中的监测量最大值、最小值、平均值及95%大值，含有丰富的用户运行信息[15]。分别以三相谐波电流含有量、谐波电流含有率的 4种监测值为分析对象，有 3× 2×4共24个样本集合。以其中一个样本集合为例，其中有24列，分别对应2至25次谐波电流的监测值。

根据现有电能质量监测存储的数据类型，本文提出基于历史监测数据的谐波主特征群筛选方法。具体的筛选步骤如下。

1）根据电能质量国家标准 GB/T 14549—1993《电能质量 公用电网谐波》以95%大值作为谐波危害分析的首选指标，且谐波电流限值为谐波电流含有量值。因此，选取一定时间范围内2至25次谐波电流含有量 95%大值建立谐波监测数据样本集X=（x1，x2，…，xi，…，x24），其中xi是i+1次谐波监测值的时序列向量。先按式（4）对各次谐波数据样本除以该次谐波电流的基准限值，得到标幺化数据样本集。

2）求取标幺化数据样本集合的协方差矩阵，并对该数据样本的协方差矩阵进行特征值分解，得到特征根λ1≥λ2…≥λi≥…≥λ24，对应的单位特征向量为γi= [γ1i，γ2i，…，γ24,i]Τ。将所求得的主成分记为y1,y2,…,yk,…,y24。

3）按式（2）确定累积方差贡献率达到80%的最小主成分数m，并用式（3）计算主成分yk与原始变量xi的相关系数ρ(yk,xi)。

4）计算谐波特征群指标Si+1。定义谐波特征群指标Si+1（i为整数且1≤i≤24）为主成分y1,y2,…,ym与xi的相关系数的平方和，如式（5）所示。

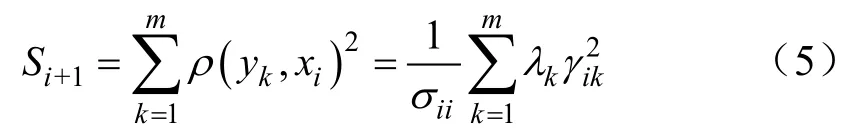
对于前m个主成分y1、y2、…、ym，Si代表了这些主成分对于原始变量的贡献率，即在这m个主成分中，包含了多少比例的变量信息。对于谐波监测数据来说，Si+1的数值越大，i+1次谐波电压或电流对于前m个主成分的贡献度就越大，也可以认为这个次数的谐波电压或电流在原数据信息中占优势地位。

5）根据Si+1的取值范围，按照以下步骤大致确定一个筛选阈值λ，通过该阈值从各次谐波中确定谐波特征群。

（1）记H为{2，3，…，i+1，…，25}，将i次谐波（i∈H）的谐波特征群指标{S2，S3，…，Si+1，…，S25}作为一个待分析数据集，记为Ω。采用上下四分位数来检测Ω的异常大值。这里假设上四分位为Q3，下四分数为Q1，四分位极差为Iqr，则Iqr的计算式如式（6）所示。

（2）在求取上述的参数值后，按照下面两个判据筛选谐波主特征群：

① 如果Q3+1.5Iqr＜1，那么λ1可取Q3+1.5Iqr，将λ1与Ω中的数值进行比较，记Ω中大于λ1的所有元素筛选出来组成新集合Λ1为{Sα1，Sα2，…，Sαt}。记Λ1内元素的下标Φ1为{α1，α2，…，αt}，其中

αi∈H，则Φ1所对应的谐波就可以作为所分析监测点用户的谐波主特征群。

② 如果Q3+1.5Iqr＞1，或者λ1取Q3+1.5Iqr作为筛选阈值时使得Λ1为空集，那么可取λ2为Q3，将Ω中大于λ2的所有元素筛选出来组成新集合Λ2为{Sβ1，Sβ2，…，Sβt}。记Λ2内每个元素的下标Φ2为{β1，β2，…，βt}，其中βi∈H，则Φ2所对应的谐波就可以作为所分析监测点用户的谐波主特征群。

经过上述步骤，可以从2～25次谐波次数中选取前t个谐波特征群指标数值较大的谐波次数，作为测点的谐波污染主特征群。

3 监测数据分析

选用福建省宁德市树太Ⅰ路测点2016年3月1日至3月10日00∶00∶00至23∶59∶59的电能质量监测数据，该数据为每10min之内的所有测点数据序列所求得的统计数据。本文以选定时间范围内a相2～25次谐波电流含有量数据的95%大值作为待分析数据。将3月1日到3月5日的测点电流谐波数据合并成一个数据集（记为数据集Ⅰ），3月6日到3月10日的测点电流谐波数据合并成一个数据集（记为数据集Ⅱ）进行分析，采用测点的谐波电流限值对数据进行标幺化处理后，进行主成分分析。

对于数据集Ⅰ，对标幺化的数据集进行主成分分析后可以发现，当m取 2时，方差贡献率ωm为82%，从而确定前两个主成分分量为数据集Ⅰ的谐波主特征群状态量。由式（5）计算得到24个谐波变量的谐波特征群指标值，见表1。

表1 数据集Ⅰ各次谐波对应的谐波特征群指标值

对于数据集Ⅱ，对标幺化的数据集进行主成分分析后可以发现，当m取 2时，方差贡献率ωm为89.06%，从而确定前两个主成分分量为数据集II的谐波主特征群状态量。由式（5）计算得到24个谐波变量的谐波特征群指标值，见表2。

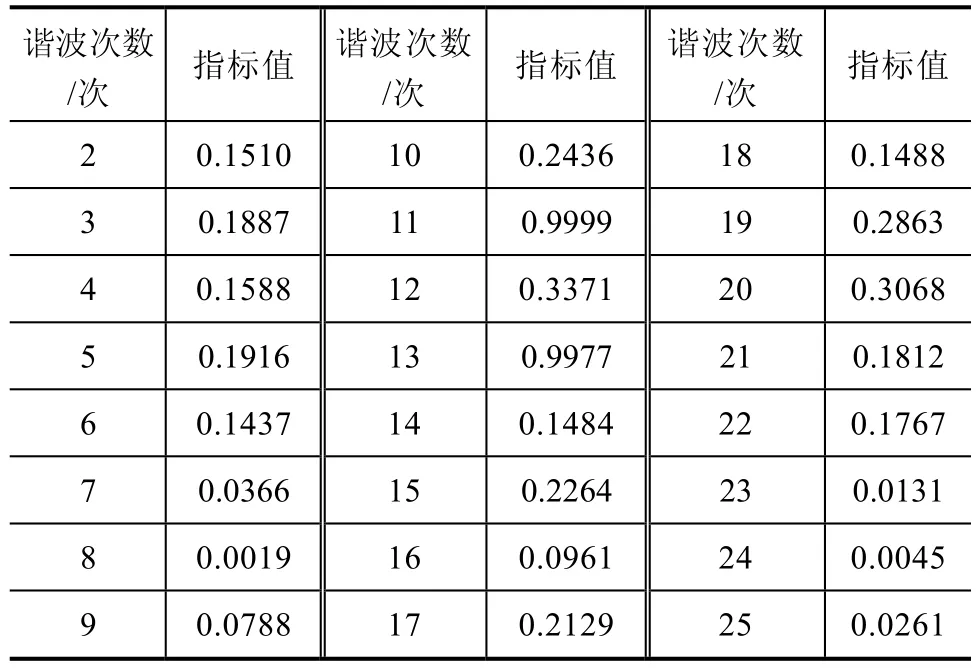
表2 数据集Ⅱ各次谐波对应的谐波特征群指标

为了便于对比，这里分别以谐波次数为横坐标，各次谐波对应的谐波特征群指标值为纵坐标，对表1和表 2中的数据以谐波次数为横坐标，谐波特征群指标为纵坐标作图，所得到的杆状图分别如图 1和图2所示。

接下来，应考虑选取合适的筛选阈值，并根据该阈值从两个数据集的指标ΩⅠ和ΩⅡ中筛选谐波主特征群。按照前述的步骤，分别计算ΩⅠ和ΩⅡ的λ1值，所得结果记为λ11和λ21，计算过程分别如式（7）和式（8）所示。

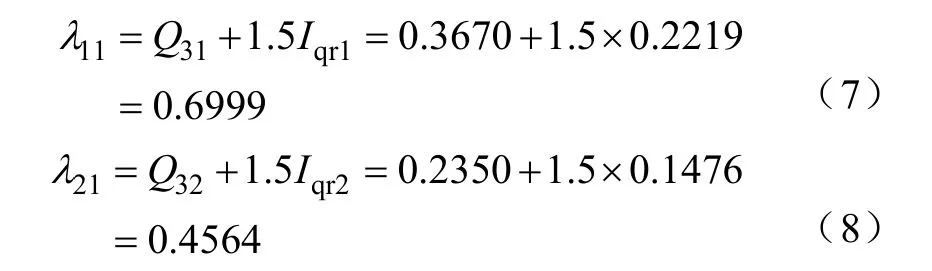
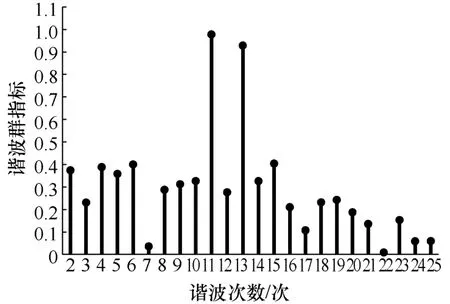
图1 数据集Ⅰ中各次谐波的谐波特征群指标杆状图

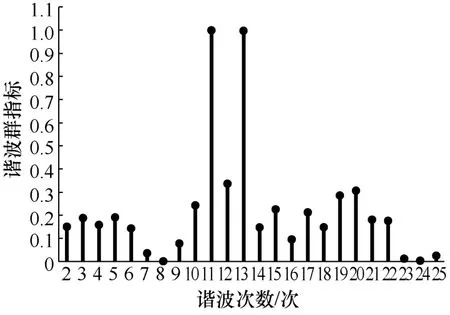
图2 数据集Ⅱ中各次谐波的谐波群指标杆状图

由于λ11和λ21均小于1，故首先选择λ11和λ21作为数据集Ⅰ和数据集Ⅱ的谐波限值特征指标的筛选阈值，从ΩⅠ和ΩⅡ中选择大于阈值的元素，组成集合ΛⅠ和ΛⅡ，其元素下标集合记为ΦⅠ和ΦⅡ。将λ11和λ21的数值用虚线在图1和图2的基础上表示出来，并对谐波特征群指标高于该数值的谐波次数（即ΦⅠ和ΦⅡ中的元素）进行标注，如图3和图4所示。

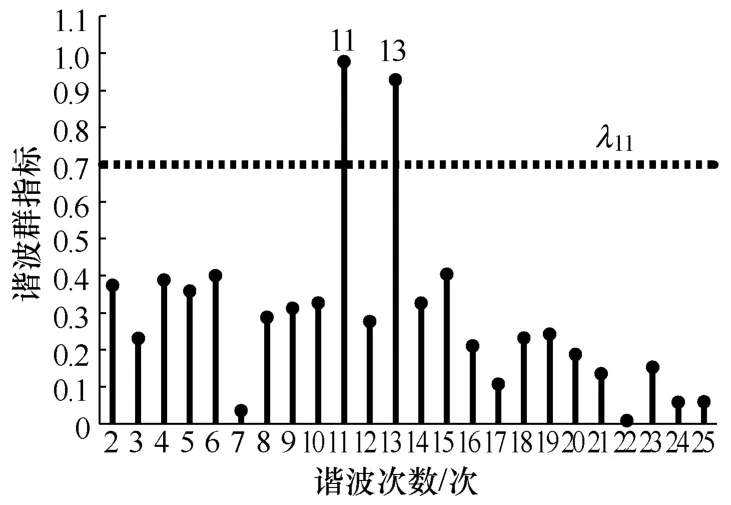
图3 图1标注筛选阈值后的谐波主特征群指标杆状图

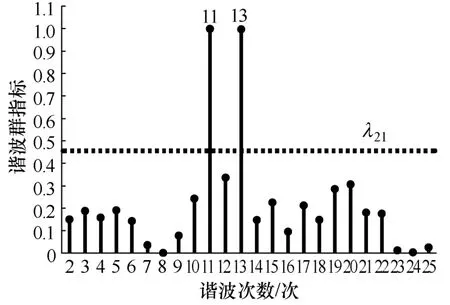
图4 图2标注筛选阈值后的谐波主特征群指标杆状图

由图 3和图 4可以看出，不论是数据集Ⅰ（3月1日到3月5日），还是数据集Ⅱ（3月6日到3月10日），通过分析得到的主特征谐波电流次数都包含11次和 13次的谐波。因此，可以将 11次和13次谐波归入树太Ⅰ路测点的谐波主特征群当中，在谐波用户的建模和治理中，需要重点考虑对该主特征群谐波次数的治理。

4 结论

电能质量在线监测系统的历史数据有助于谐波污染用户建模，但完备的谐波模型包含相互影响的谐波电压和谐波电流监测指标，这使得模型非常复杂而无法实现参数辨识。出于工程实践需要，需要从大量历史监测数据中确定谐波主特征群，以便针对谐波主特征群建立工程实用模型。

基于以上需求，本文提出一种基于历史监测数据的谐波主特征量确定方法，利用统计分析中常用的主成分分析方法，从在线监测数据中提取能够用于谐波分析的主特征群。此后，利用宁德市配电网的电能质量监测数据进行上述分析，验证了该方法在工程上的可行性。通过建立用户的谐波特征群，可以在用户负荷类型未知情况下，基于用户日常的电能质量监测数据，对用户主要的谐波污染进行跟踪，为简化谐波用户建模和有效地治理谐波污染提供可靠的依据。

[1]裴林,郑建辉,孙怡.电能质量综合监测管理系统的研究[J].电力系统保护与控制,2008,36(23)：49-53.

[2]Emanuel A E.On the assessment of harmonic pollution[J].IEEE Trans on Power Delivery,1995,10(3)：1693-1698.

[3]Modelling and simulation of the propagation of harmonics in electric power networks I：Concepts,models,and simulation techniques [J].IEEE Trans on Power Delivery,1996,11(1)：452-465.

[4]冯士刚,艾芊,徐伟华,等.基于瞬时对称分量的负荷谐波建模[J].高电压技术,2008,34(4)：783-787.

[5]冯士刚,艾芊.一种谐波负荷建模的新方法[J].电力系统自动化,2007,31(17)：26-30.

[6]Fauri M.Harmonic modelling of non-linear load by means of crossed frequency admittance matrix[J].IEEE Trans on Power Delivery,1997,12(4)：1632-1638.

[7]赵勇,张涛,李建华,等.一种新的谐波源简化模型[J].中国电机工程学报,2002,22(4)：46-51.

[8]杨洪耕,王磊.基于拉盖尔多项式的非线性负荷谐波发射水平估计[J].中国电机工程学报,2005,25(7)：81-85.

[9]王磊.用概率密度函数近似计算谐波发射水平[J].高电压技术,2007,33(11)：198-200,212.

[10]徐文远,雍静.电力扰动数据分析学—电能质量监测数据的新应用[J].中国电机工程学报,2013(19)：93-101.

[11]吴笃贵,徐政.电力负荷的谐波建模[J].电网技术,2004,28(3)：20-24.

[12]周胜军,林海雪.并联电容器装置的谐波简化分析与计算[J].供用电,2009,26(1)：4-9.

[13]黄宁.关于主成分分析应用的思考[J].数理统计与管理,1999,18(5)：44-46.

[14]何晓群.多元统计分析[M].北京：中国人民大学出版社,2004.

[15]张逸,林焱,吴丹岳.电能质量监测系统研究现状及发展趋势[J].电力系统保护与控制,2015(2)：138-147.

The Method for Screening the Principal Characteristic Group of Harmonic Pollution Using the Historical Monitoring Data

Lin Kunjie1Pan Xia2Zhang Yan1Shao Zhenguo1
(1.College of Electrical Engineering and Automation,Fuzhou University,Fuzhou 350116；2.Electric Power Bureau of Ningde,Ningde,Fujian 352000)

The mutual influence between different harmonic orders need to be considered in coupling model of harmonic pollution,which makes the model complex.This paper introduces a method for screening the principal characteristic group of harmonic pollution based on the historical monitoring data.Firstly,principle component analysis (PCA) is used for calculating index of harmonic characteristics via the correlation coefficient between the principal components and original variables.Then the principal characteristic group is extracted from historical monitoring data in terms of aforementioned index.Finally,the feasibility of proposed method is verified via a case study on power quality monitoring data gathered form distribution network of Ningde.

plug-bushing；harmonic；principal characteristic group；principal component analysis；power quality monitoring

林坤杰（1991-），男，福建省漳州人，硕士研究生，研究方向为电能质量。

福建省科技计划重点项目（2013H0024）

福建省自然科学基金项目（2016J01219）