三角变换中的“目标意识”和“整体思维”

胡 琳

(河北省石家庄市第一中学 050000)

三角变换的实质为“依据目标意识，挖掘题设条件，寻求差异，整体思维选用三角公式变名，变角，变结构”完成求值，化简，证明等问题.其中“目标意识，整体思维，凑角入手，消除差异，合理选用公式”起着决定性的作用.

一、目标意识，整体思维，凑角入手，消除差异建立函数关系

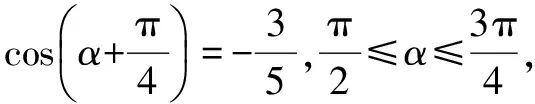
简析寻求角的差异如何沟通？目标意识求cos2α,sin2α，变名入手沟通角之间的关系，

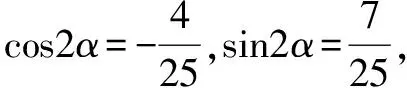
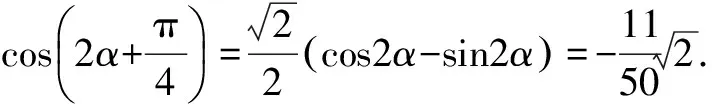
二、目标意识，改变结构，出现“特殊值，消项，约项”求解

简析整体思维，注意结构特征为分式，改变结构其目标为约项求值.可用平方差公式，辅助角二倍角公式逆用约项.

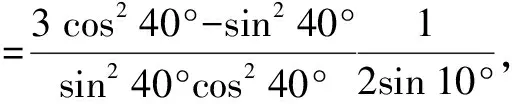
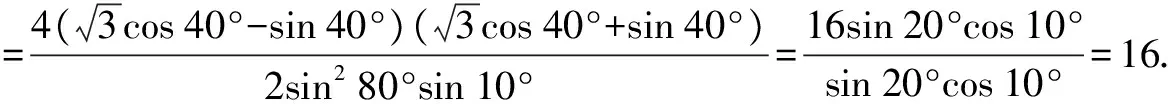
三、目标意识，整体思维，平方消参，消除差异求解

例3 已知 1+cosα-sinβ+sinαsinβ,1-cosα-cosβ+sinαcosβ=0,求sinα.

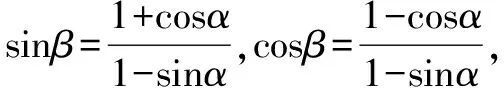
四、目标意识，整体思维，方程(组)观念，消除差异求解

例4 已知F(θ)=cos2θ+ccos2(θ+α)+cos2(θ+β),问是否存在满足0≤α≤β≤π的α，β使得F(θ)的值不随θ的变化而变化?如果存在，求出θ的值；若不存在，请说明理由.

简析条件的探索及常函数的认识，分离参数构建方程组求解.要使得F(θ)的值不随θ的变化而变化，需使得θ的系数为0，故需把θ与α，β分离，转化为cosθ或sinθ的多项式，需要目标意识，整体思维降次应用公式.

由常函数的意义，构建方程组有 1+cos2α+cos2β=0,sin2α+sin2β=0.三角变换目标意识“平方消参降元”求得.即使F(θ)的值不随θ的变化而变化的α=π/3，β=2π/3存在.

五、目标意识，整体思维，换元沟通变量之间的关系求解

例5 求函数y=sinxcosx+sinx+cosx的最大值.

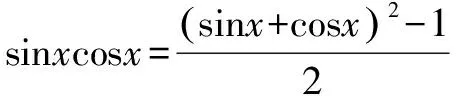
注：试回味最值求解中函数关系是如何建立的？体验三角综合问题中的“目标意识、整体思维”的指导作用.

六、目标意识，整体思维,变形用公式求解

例6 求(1+tan1°)(1+tan2°)(1+tan3°)…(1+tan44°)(1+tan45°)的值.

于是，整体变形有，

原式=

[(1+tan1°)(1+tan44°)][(1+tan2°)(1+tan43°)]…

[(1+tan22°)(1+tan23°)](1+tan45°)=2·2·…·2=223.

七、目标意识， 整体思维，构造对偶式求解

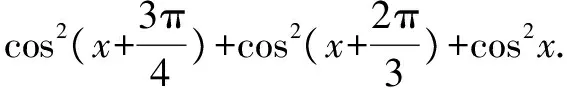
简析通法为降次化积“消项”求值.若注重平方关系和倍角公式，构造对偶式解方程组求解“具有操作性”.

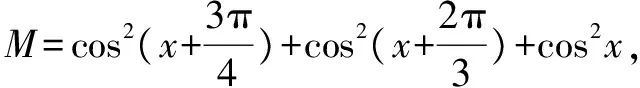
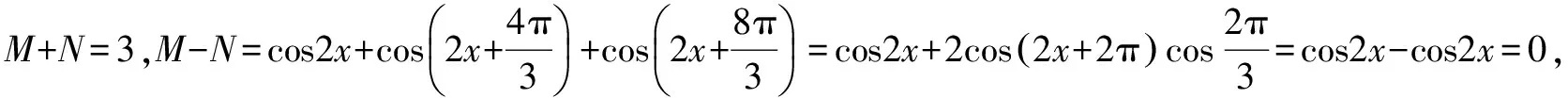
八、目标意识，整体思维，构造“辅助因子法”求解

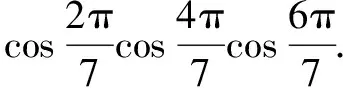
简析角成等比数列的余弦之积，整体把握二倍角公式，乘以最小角的正弦，二倍角公式连锁反应，“约项”求值.

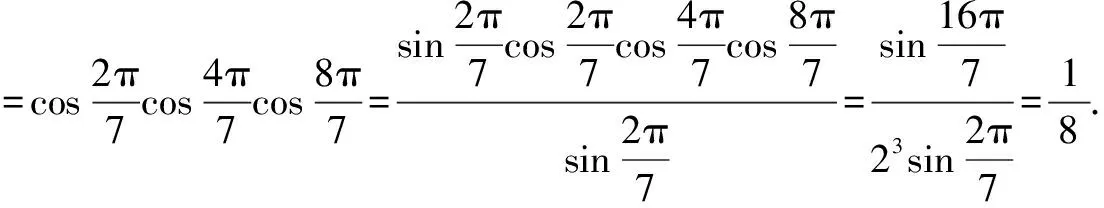
[1]白鹏恩.三角变换的基本方法[J].山西教育·高考理科,2005(10).