Solvability for a Coupled System of Fractional p-Laplacian Diferential Equations at Resonance
ZHOU HUI,ZHOU ZONG-FUAND WANG LI-PING
(1.School of Mathematics and Statistics,Hefei Normal University,Hefei,230601)
(2.School of Mathematical Science,Anhui University,Hefei,230601)
Solvability for a Coupled System of Fractional p-Laplacian Diferential Equations at Resonance
ZHOU HUI1,2,ZHOU ZONG-FU2,*AND WANG LI-PING2
(1.School of Mathematics and Statistics,Hefei Normal University,Hefei,230601)
(2.School of Mathematical Science,Anhui University,Hefei,230601)
Communicated by Shi Shao-yun
In this paper,by using the coincidence degree theory,the existence of solutions for a coupled system of fractional p-Laplacian diferential equations at resonance is studied.The result obtained in this paper extends some known results.An example is given to illustrate our result.
p-Laplacian,coincidence degree,existence,fractional diferential equation,boundary value problem
1 Introduction
In this paper,by using the coincidence degree theory,we discuss the existence of solutions to a coupled system of fractional p-Laplacian diferential equations at resonance:
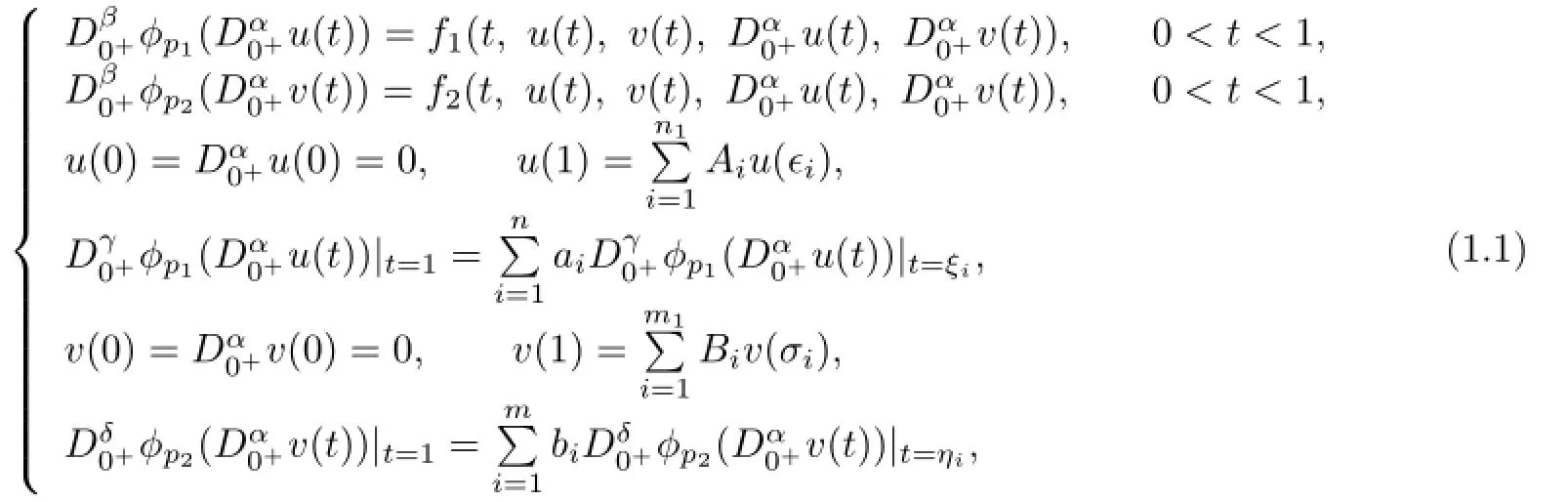
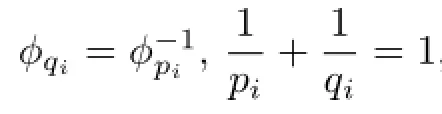
In this paper,we always suppose that the following conditions hold.
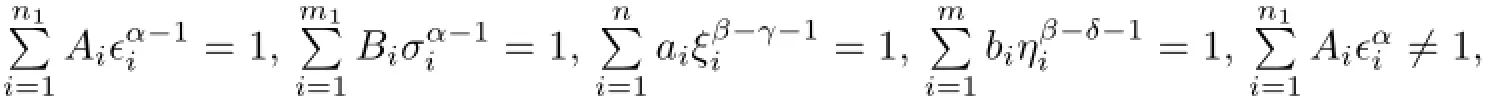
(H2)fi:[0,1]×R4→Rsatisfed Carath´eodory conditions,i=1,2,that is,
(i)f(·;x1,x2,x3,x4):[0,1]→Ris measurable for all(x1,x2,x3,x4)∈R4;
(ii)f(t;·,·,·,·):R4→Ris continuous for a.e.t∈[0,1];
(iii)for each compact set K⊂R4there is a function φK∈L∞[0,1]such that
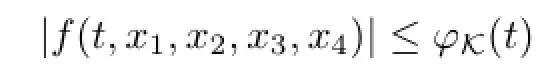
for a.e.t∈[0,1]and all(x1,x2,x3,x4)∈K.
The existence of solutions for boundary value problem of integer order diferential equations at resonance has been studied by many authors(see[1]–[10]and references cited therein).Since the extensive applicability of fractional diferential equations(see[11]and [12]),recently,more and more authors pay their close attention to the boundary value problems of fractional diferential equations(see[13]–[20]).In papers[13]and[14],the existence of solutions to coupled system of fractional diferential equations at nonresonance has been given.In papers[15]and[16],the solvability of fractional diferential equations at resonance has been investigated.
Paper[16]investigates the following coupled system of fractional diferential equations at resonance:
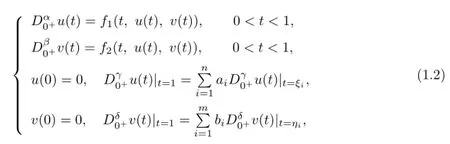
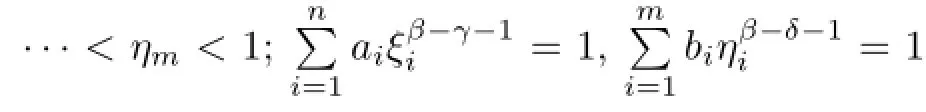
In the past few decades,in order to meet the demands of research,the p-Laplacian equation is introduced in some BVP,such as[17]and[18].
The turbulent fow in a porous medium is a fundamental mechanics problem.For studying this type of problems,Leibenson[17]introduced the p-Laplacian equation as follows
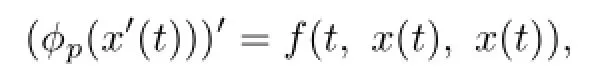
Paper[18]investigated the existence of solutions for the BVP of fractional p-Laplacian equation with the following form
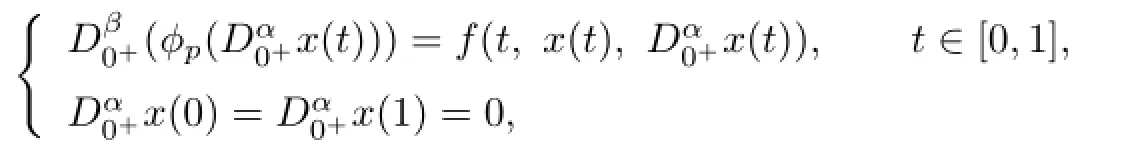
where 0<α,β≤1 with 1<α+β≤2,and p>1,ϕp(s)=|s|p−2s is a p-Laplacian operator, Dαis a Caputo fractional derivative.By using the coincidence degree theory,a new result on the existence of solutions for the above fractional boundary value problem is obtained.
Inspired by above works,our work presented in this paper has the following new features. On the one hand,the method used in this paper is the coincidence degree theory and the system has p-Laplacian,which bring about many argument difculties.On the other hand,our study is on fractional p-Laplacian diferential system with multipoint boundary conditions.To the best of our knowledge,there are relatively few results on boundary value problems for fractional p-Laplacian equations at resonance.We fll this gap in the literature. Hence we improve and generalize the results of previous papers to some degree,and so it is interesting and important to study the existence of solutions for system(1.1).
This paper is organized as follows.In Section 2,we present the transformation of the system(1.1),some results of fractional calculus theory and some lemmas,which are used in the next two sections.In Section 3,basing on the coincidence degree theory of Mawhin[19], we get the existence of solutions for system(1.1).In Section 4,one example is given to illustrate our result.Our result is diferent from those of bibliographies listed above.
2 Preliminaries
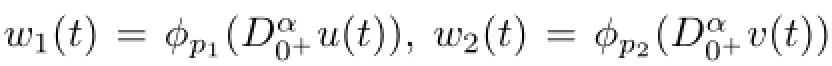
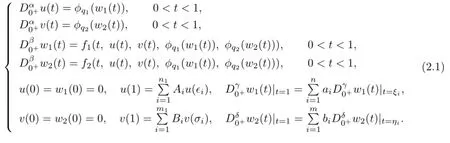
Clearly,if x(t)=(u(t),v(t),w1(t),w2(t))Tis a solution of(2.1),then(u(t),v(t))Tmust be a solution of(1.1).So the problem of fnding a solution for(1.1)is converted to fnd a solution for(2.1).
Next we present here the necessary defnitions and Lemmas from fractional calculus theory.These defnitions and Lemmas can be found in the recent literatures[11]and[12].
Defnition 2.1[11]The fractional integral of order α>0 of a function f:(0,∞)→Ris defned by
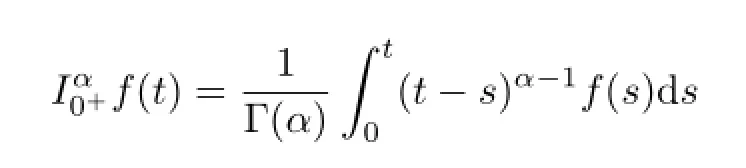
provided that the right-hand side exists.
Defnition 2.2[11]The Riemann-Liouville fractional order derivative of order α∈(n−1,n]of a function f:(0,∞)→Ris defned by
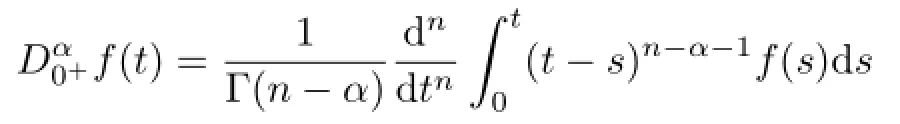
provided that the right-hand side exists.
Lemma 2.1[12]Assume that f∈L[0,1],q>p≥0.Then
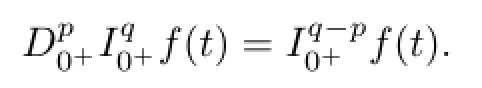
Lemma 2.2[12]Assume that α>0,λ>−1.Then
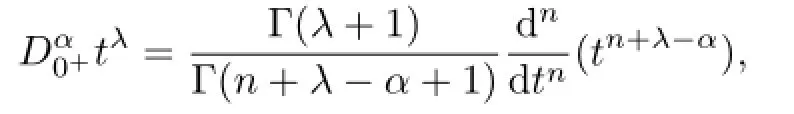
where n=[α]+1.
Lemma 2.3[12]Let α∈(n−1,n],u∈C(0,1)∩L1(0,1).Then
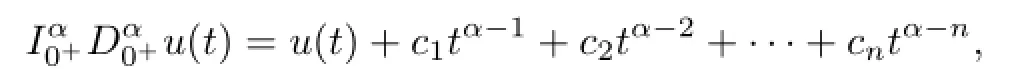
where ci∈R,i=1,2,···,n.
Now,we briefy recall some notations and an abstract existence result,which can be found in[19].
Let X,Y be real Banach spaces,L:domL⊂X→Y be a Fredholm operator with index zero,and P:X→X,Q:Y→Y be projectors such that ImP=kerL,ImL=kerQ.then

and
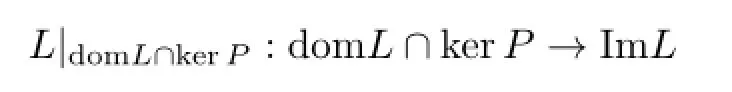
is invertible.We denote the inverse by KP.
If Ω is an open bounded subset of X such that domL∩Ø,then the map N:X→Y will be called L-compact on¯Ω if QN(¯Ω)is bounded and KP(I−Q)N:¯Ω→X is compact.Lemma 2.4[19]Let L:domL⊂X → Y be a Fredholm operator with index zero and N:X→Y be L-compact on.Assume that the following conditions are satisfed:
(1)Lx/=λNx for every(x,λ)∈[(domLkerL)∩∂Ω]×(0,1);
(2)Nx/∈ImL for every x∈kerL∩∂Ω;
(3) deg(JQN|kerL,Ω∩kerL,0)/=0,where J:ImQ → kerL is a isomorphism, Q:Y→Y is a projection such that ImL=kerQ.
Then the equation Lx=Nx has at least one solution in domL∩¯Ω.
Let
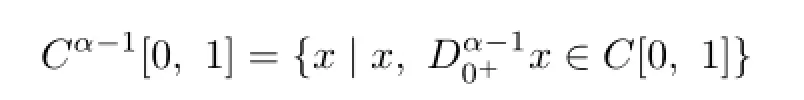
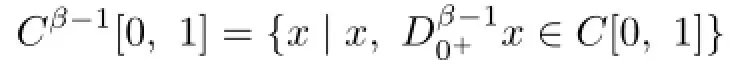
Set

with norm
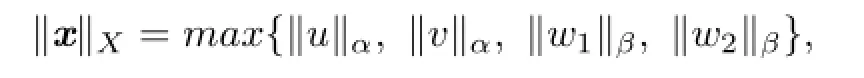
and
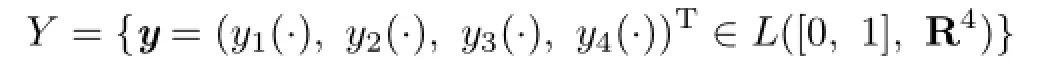
with norm
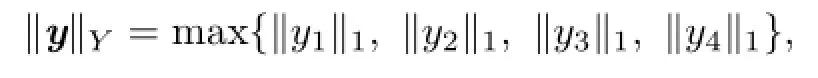
Defne the operator L:domL⊂X→Y by
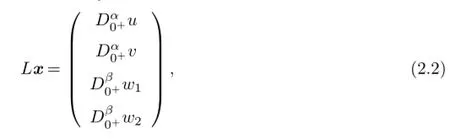
where
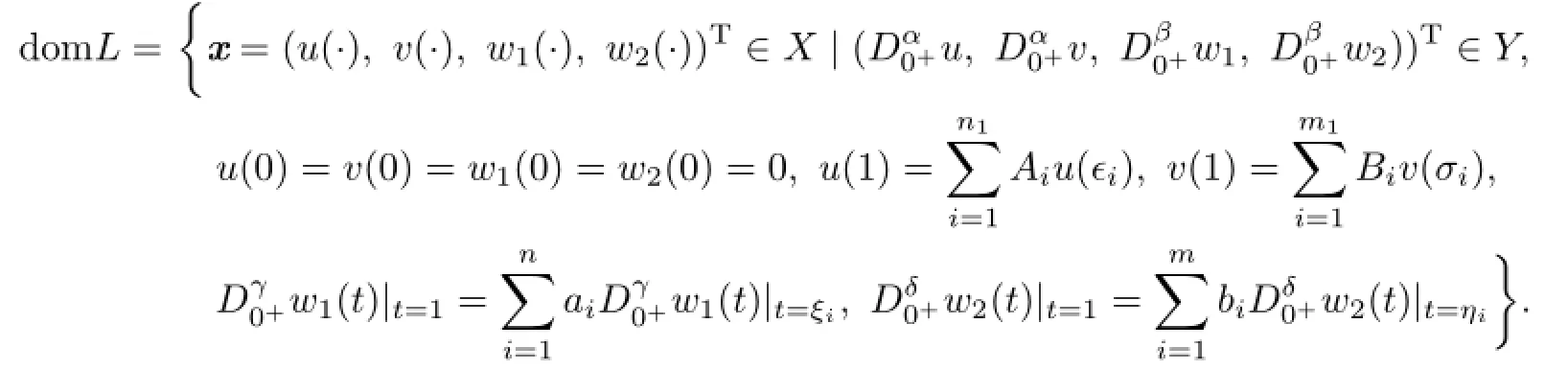
Let N:X→Y be the operator
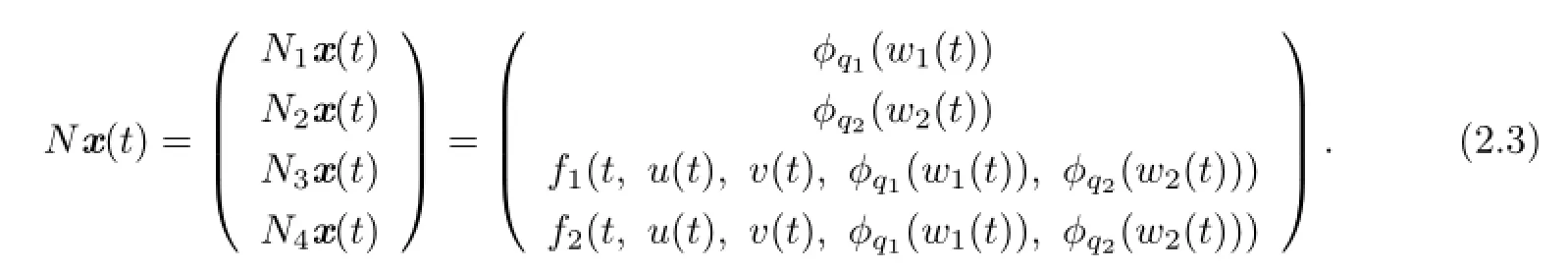
Then BVP(2.1)is equivalent to the operator equation
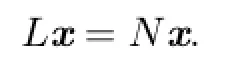
3 Main Results
Defne operators T1,T2,T3,T4:L[0,1]→Ras follows:
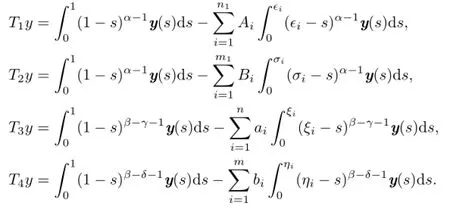
In order to obtain our main results,we frst present the following lemmas.
Lemma 3.1Suppose that(H1)holds,and let L be defned by(2.2).Then
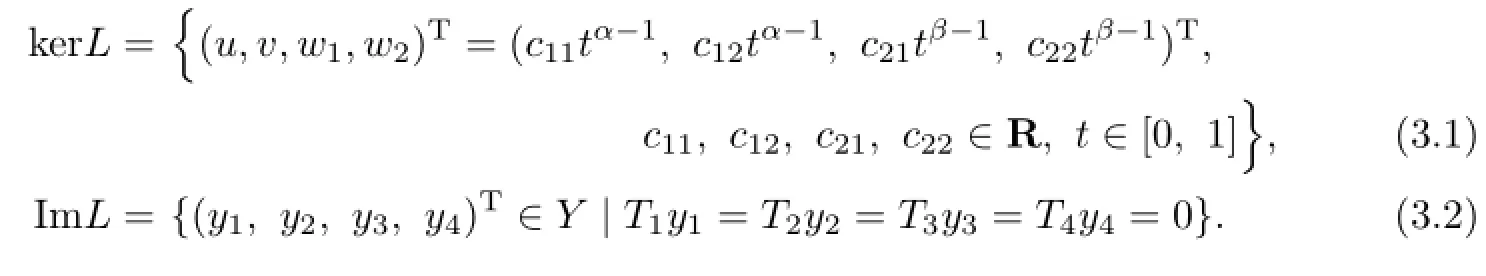
Proof. Since(u,v,w1,w2)T∈kerL,we get
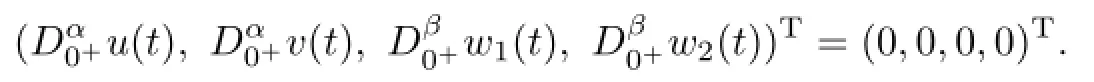

Combining with the boundary value condition u(0)=0,we get e11=0.So

Likewisely,

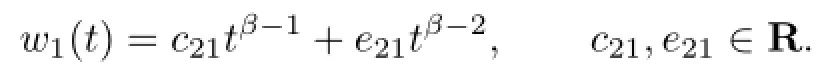
Together with the boundary value condition w1(0)=0,we get e21=0.So
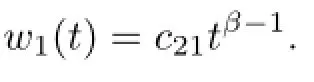
Likewisely,
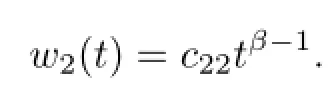
One has that(3.1)holds.
If y=(y1,y2,y3,y4)T∈ImL,then there exists an x=(u,v,w1,w2)T∈domL such that Lx=y.That is,

Basing on Lemma 2.3,we have
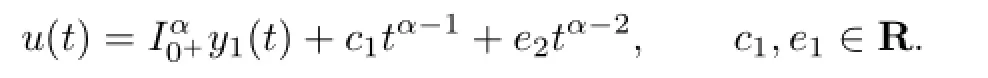

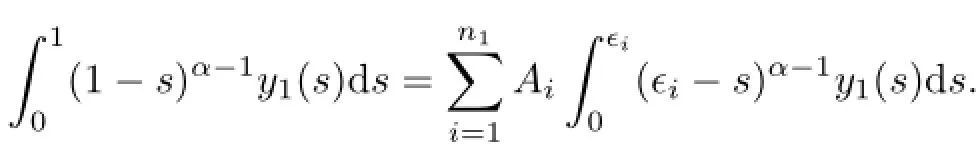
Likewisely,y2satisfes
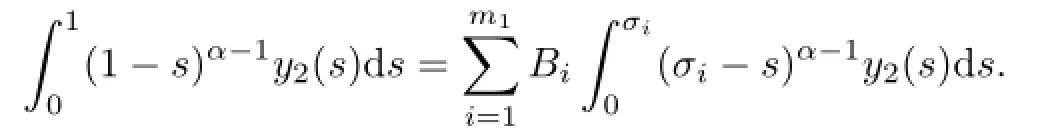
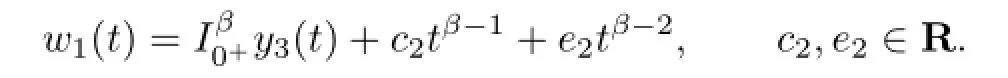
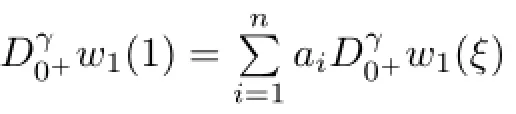
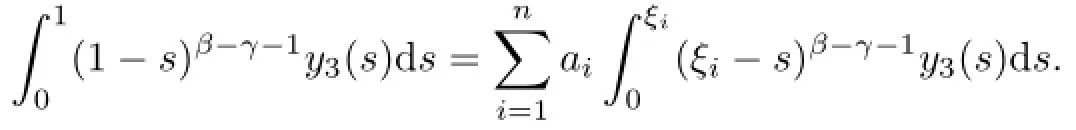
Similarly,by Lemma 2.3,we have
Likewisely,y4satisfes
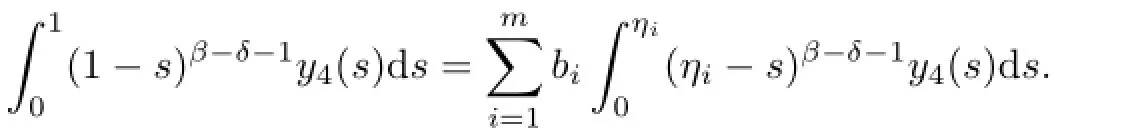
So,
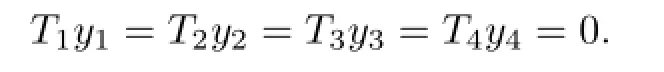
That is,
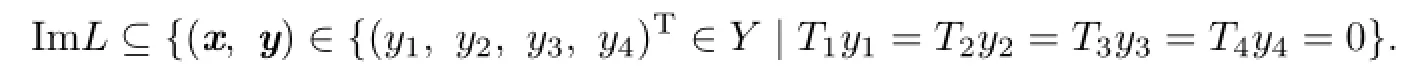
On the other hand,let y=(y1,y2,y3,y4)T∈Y satisfy T1y1=T2y2=T3y3=T4y4=0, and x=(u,v,w1,w1)T.Take
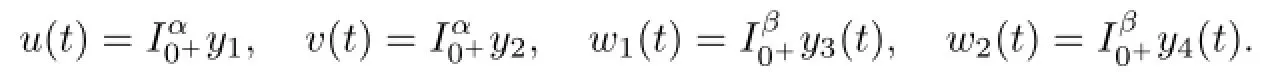
It follows from Lemma 2.1 that
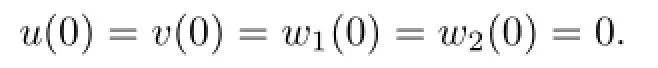
By T1y1=T2y2=T3y3=T4y4=0,we get that u,v,w1,w2satisfy
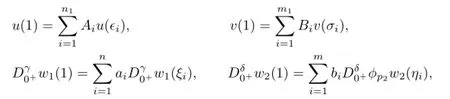
respectively.So,(u,v,w1,w2)T∈domL,we get(y1,y2,y3,y4)T∈ImL.That is,

The proof of Lemma 3.1 is completed.
Lemma 3.2Let L be defned by(2.2).If(H1)holds,then L is a Fredholm operator of index zero,and the linear continuous projector operators P:X→X and Q:Y→Y can be defned as
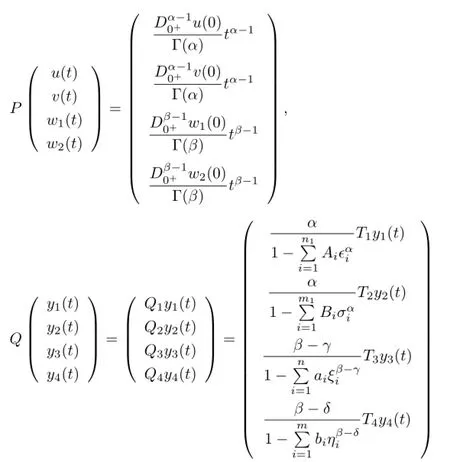
for t∈[0,1],and the operator KP:ImL→domL∩kerP can be written as

where KPis the inverse of L|domL∩kerP.
Proof. We divide the proof into two steps.
Step 1.We prove that L is a Fredholm operator of index zero.
(I)Since Lemma 3.1,we know
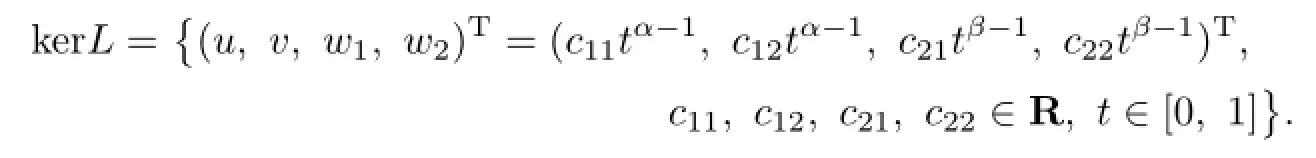
By u(t)=c11tα−1and Lemma 2.2,we get
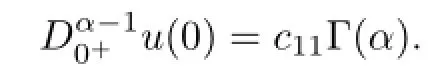
So
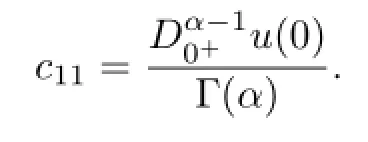
Likewisely,
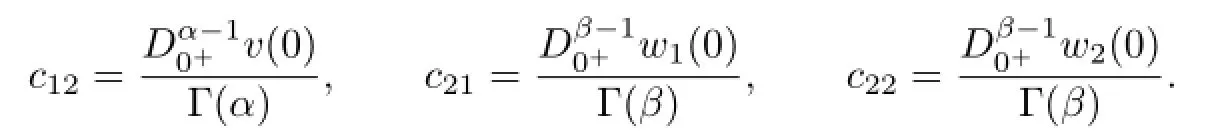
So ImP=kerL.
We show that P2(u,v,w1,w2)T=P(u,v,w1,w2)Tin the follows.In fact,by Lemma 2.2,we get
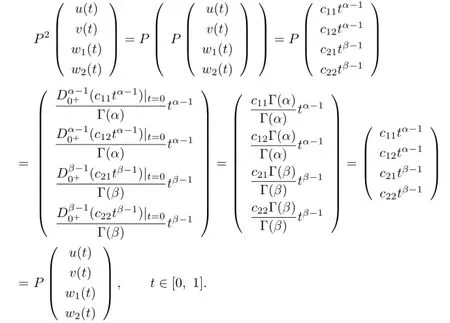
Then P is the linear continuous projector operator.So,we have X=kerL⊕kerP.
(II)For y=(y1,y2,y3,y4)T∈Y,we prove Q2y=Qy,that is,Q2iyi=Qiyi,i= 1,2,3,4.In fact,
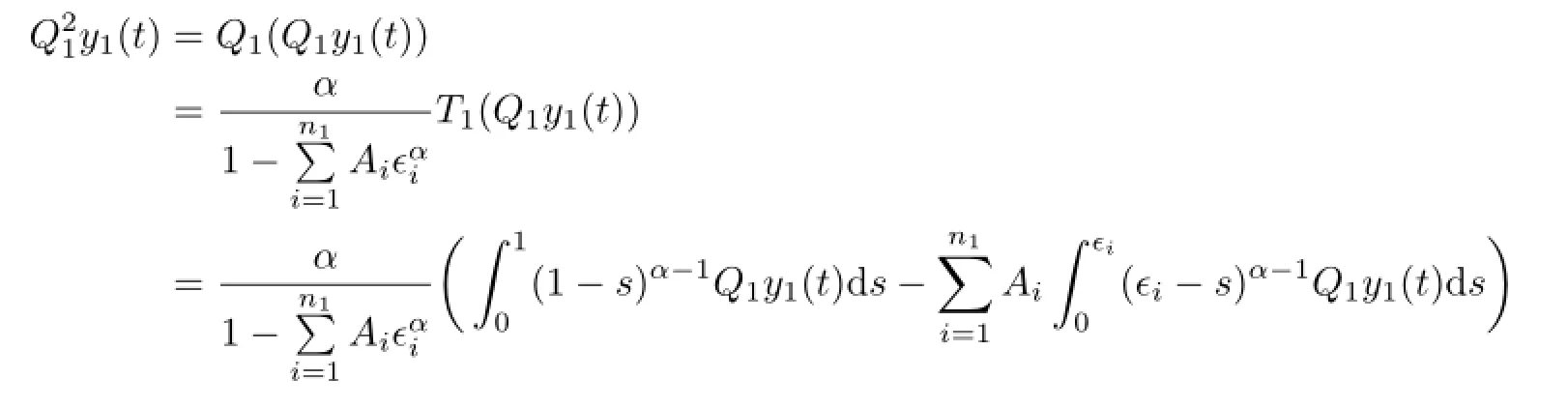

Likewisely,
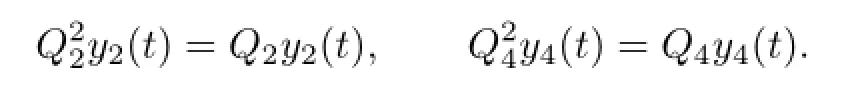
So
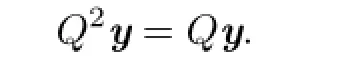
From the defnition of Q and(3.2),we can easily get that

So,we have
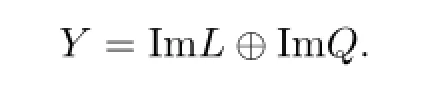
Thus

This means that L is a Fredholm operator of index zero.
Step 2.We prove that the inverse of L|domL∩kerPis KP.
For y=(y1,y2,y3,y4)T∈ImL,z=(z1,z2,z3,z4)T,let z=KPy,that is,z satisfy zi=KPiyi,i=1,2,3,4,and z∈domL∩kerP.Since LKPy=y,we get Lz=y.By(2.2), we know
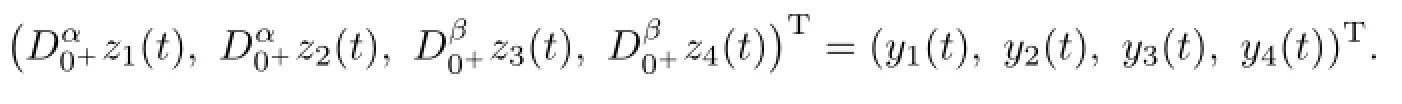
By Lemma 2.3,we have
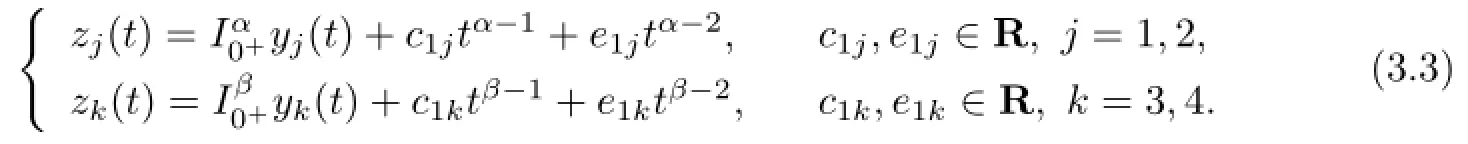
By z∈domL,we know zi(0)=0,i=1,2,3,4.So,

By z∈kerP,we know

It follows from(3.3)–(3.4)and Lemma 2.2 that
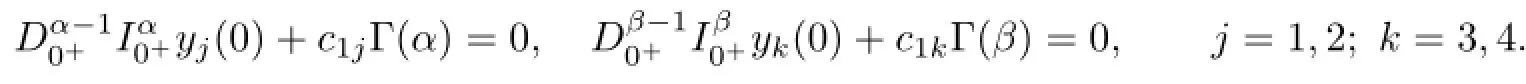
We get

It follows from(3.3)–(3.5)that
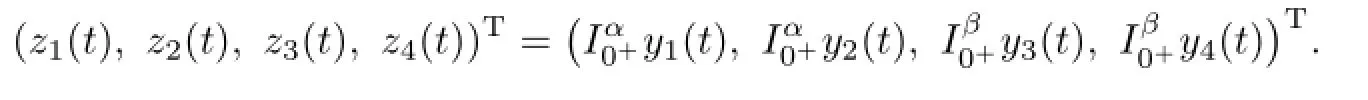
That is,

The proof of Lemma 3.2 is completed.
Lemma 3.3Suppose that(H1)and(H2)hold.If Ω⊂X is an open bounded subset and domL∩¯Ω/=Ø,then N is L-compact on¯Ω.
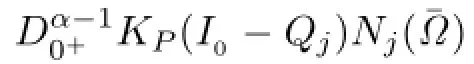
(i)The condition(H2)and the continuity of ϕq1,ϕq2mean that there exist constant Mi>0 such that
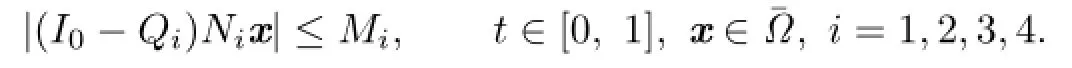
For x∈¯Ω,t∈[0,1],we have
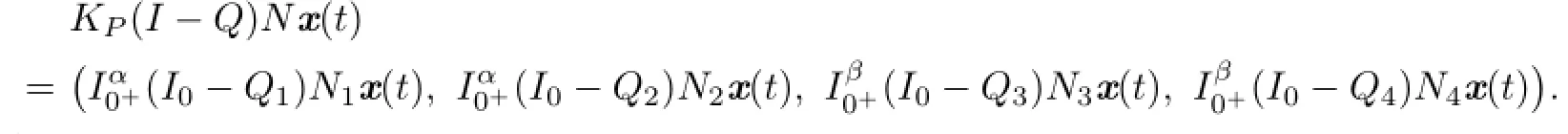
And we can know
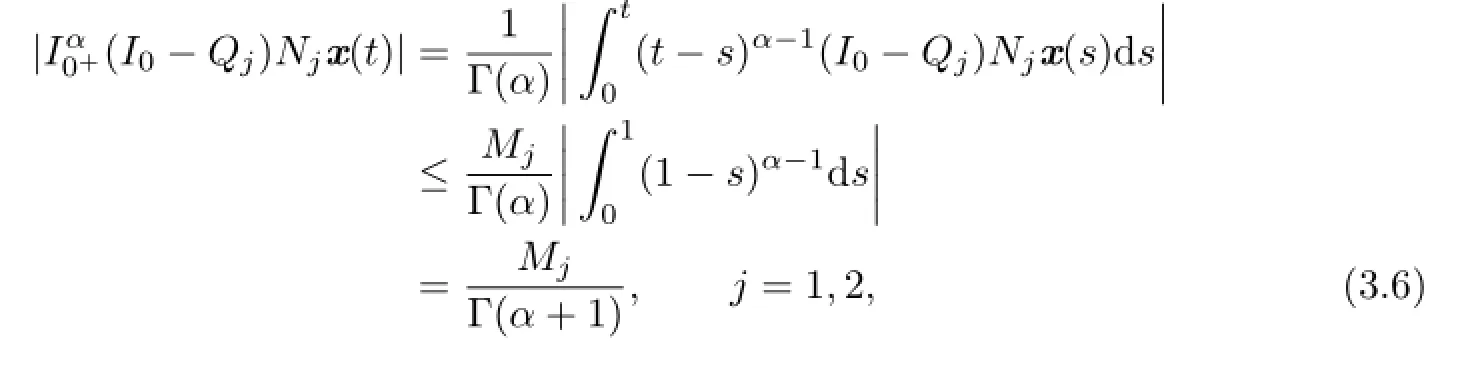
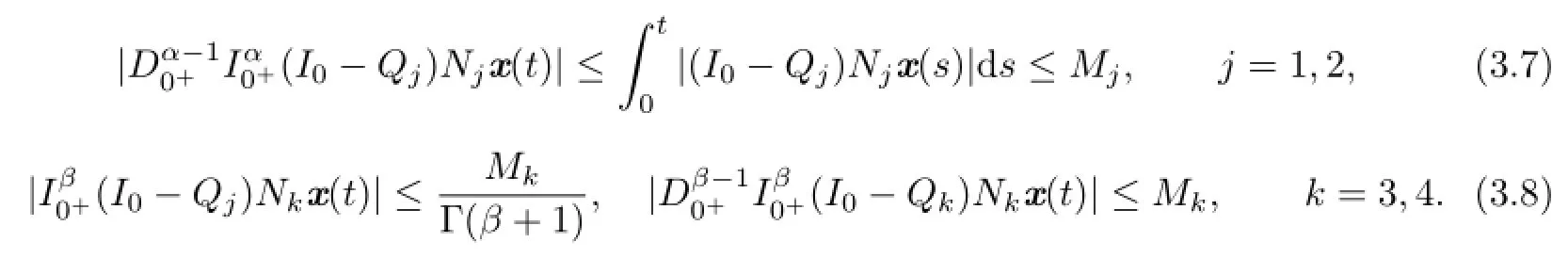
From(3.6)–(3.8),we get
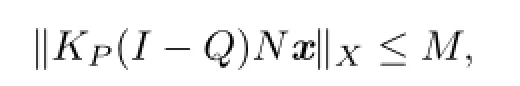
(ii)For 0≤t1<t2≤1,x∈,we have
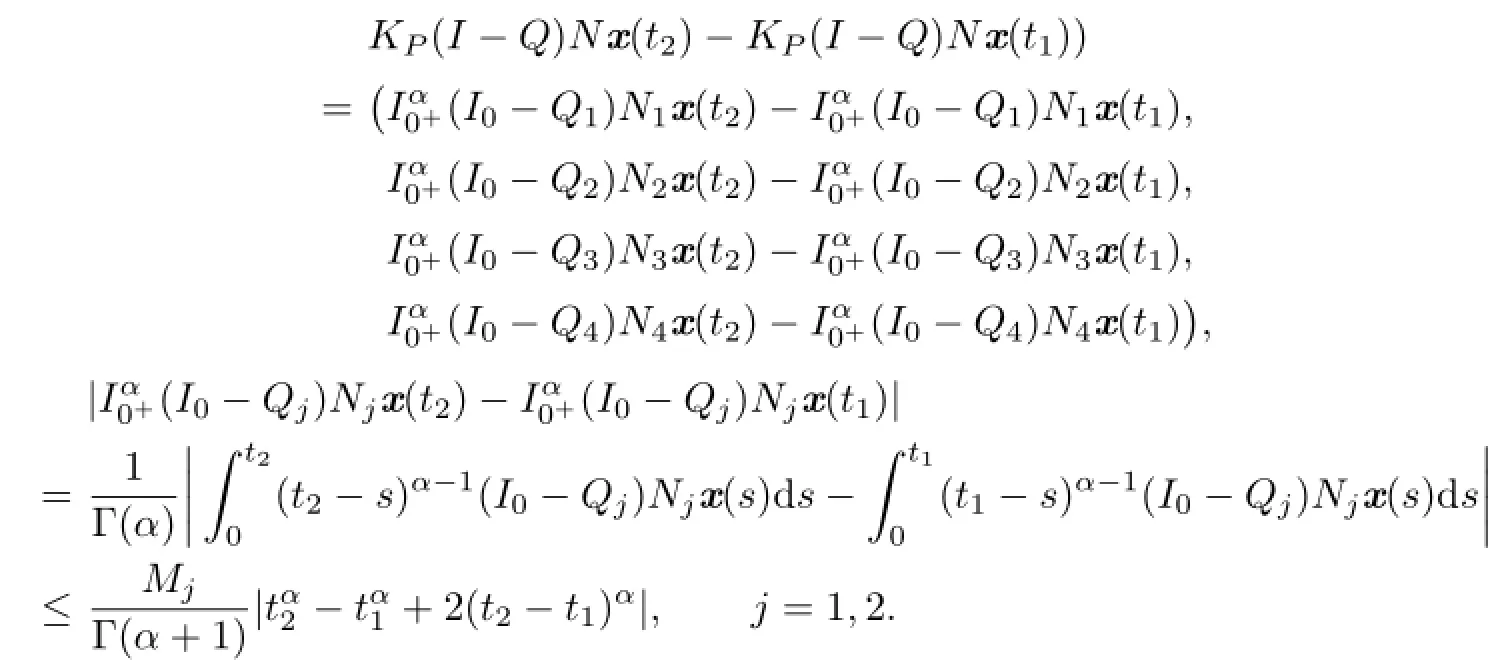
By Lemma 2.1,we get
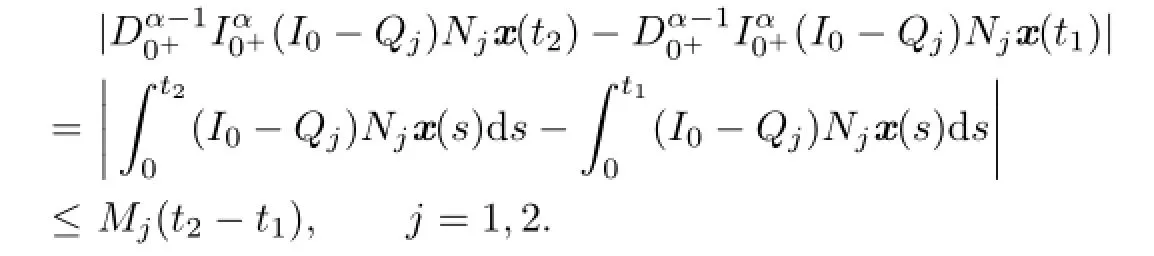
Similarly,we get
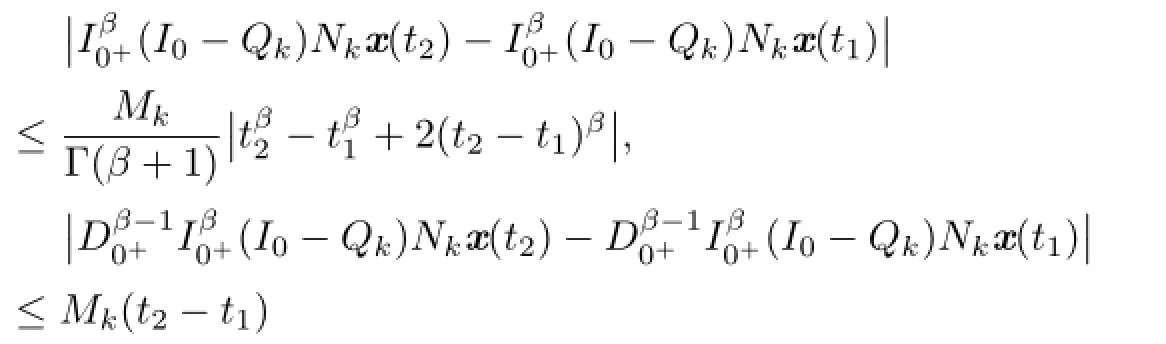
for k=3,4.
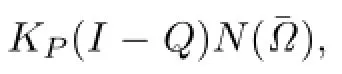
Applying the Arzel`a-Ascoli theorem,we get KP(I−Q)N:→X is compact.So,N is L-compact on.The proof of Lemma 3.3 is completed.
To obtain our main results,we need the following conditions.
(H3)There exist functions ζi,ψi,φi,hi,gi∈L[0,1],i=1,2,such that
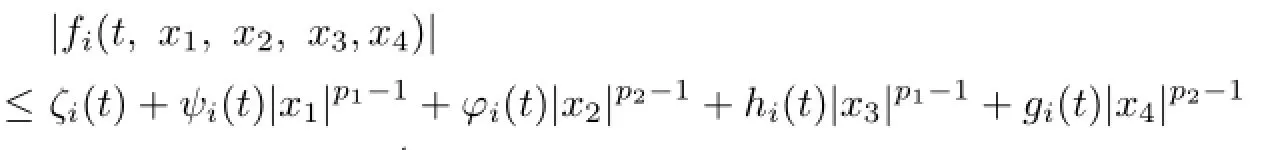
for t∈[0,1],(x1,x2,x3,x4)∈R4,where ψi,φi,hi,gi,i=1,2,satisfying
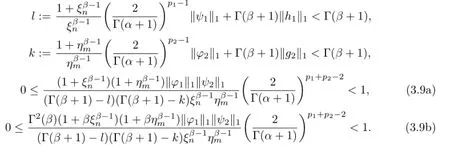
(H4)For x∈domL,there exist constants Ri>0,i=1,2,3,4,such that if at least one of the inequations
(1)|u(t)|>R1,t∈[ϵn1,1];
(2)|w1(t)|>R3,t∈[ξn,1];
(3)|v(t)|>R2,t∈[σm1,1];
(4)|w2(t)|>R4,t∈[ηm,1]
holds,then at least one of the following inequations holds:
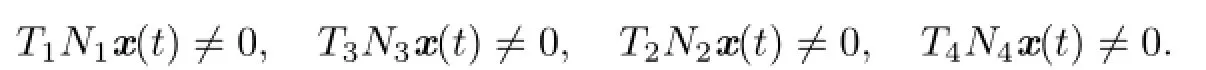
(H5) For x=(c1tα−1,c2tα−1,c3tβ−1,c4tβ−1)T∈kerL,there exist constants ei>0, i=1,2,3,4,such that either
(1)ciTiNix>0 if|ci|>ei,i=1,2,3,4,
or
(2)ciTiNix<0,if|ci|>ei,i=1,2,3,4
holds.
Lemma 3.4Suppose that(H1)–(H4)hold.Then the set
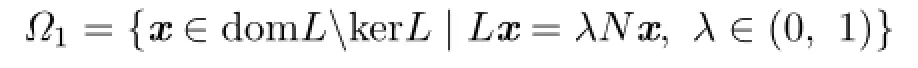
is bounded in X.
Proof.Take
By Lx=λNx,Lemma 2.3 and(u(0),v(0),w1(0),w2(0))T=(0,0,0,0)T,we have
By Nx∈ImL,we get
These,together with(H4),mean that there exist constants t11∈[ϵn1,1],t1∈[ξn,1], t22∈[σm1,1],t2∈[ηm,1]such that

By(3.10),we have
By Lemma 2.3,we have

that is,

Similarly,we have

By(3.10)–(3.12),we know

which together with

(see[20])and(3.13)–(3.14),we get
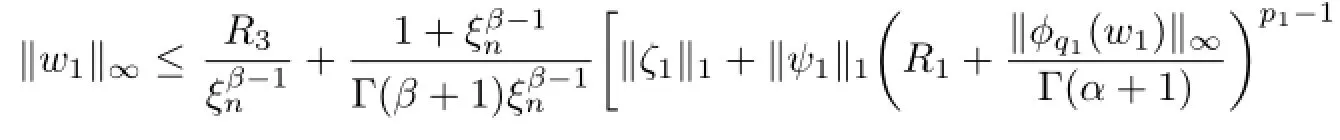
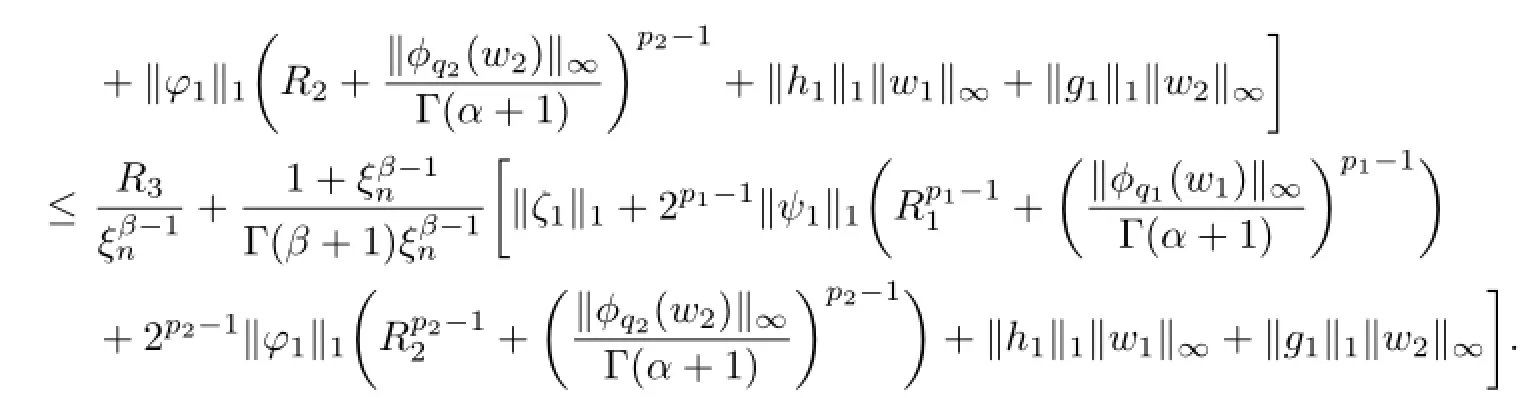
So

Likewisely,
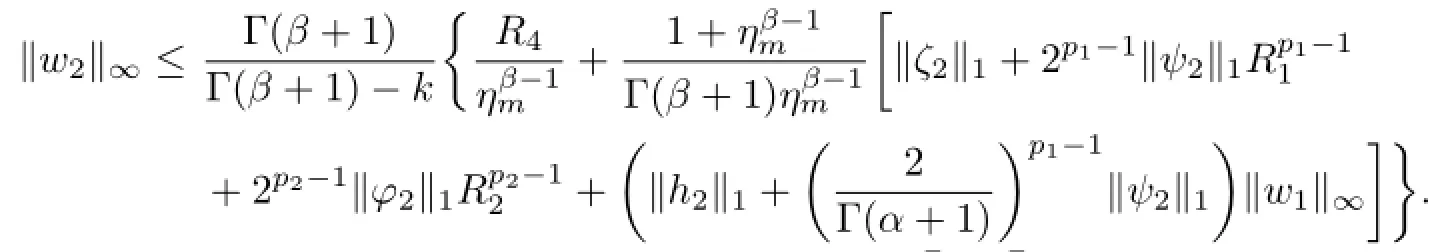
In view of(3.9a),we can see that there exist constants,>0 such that
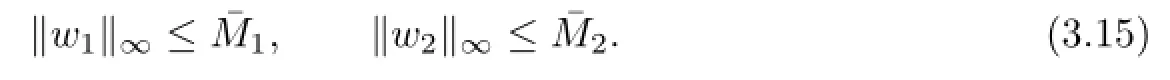
So

Combing(3.13)with(3.14),we get
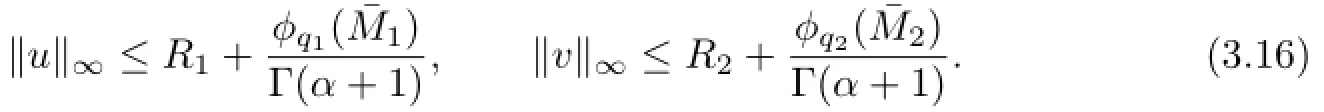
On the other hand,by(3.10),we have
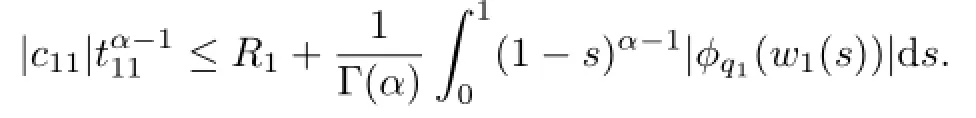
So
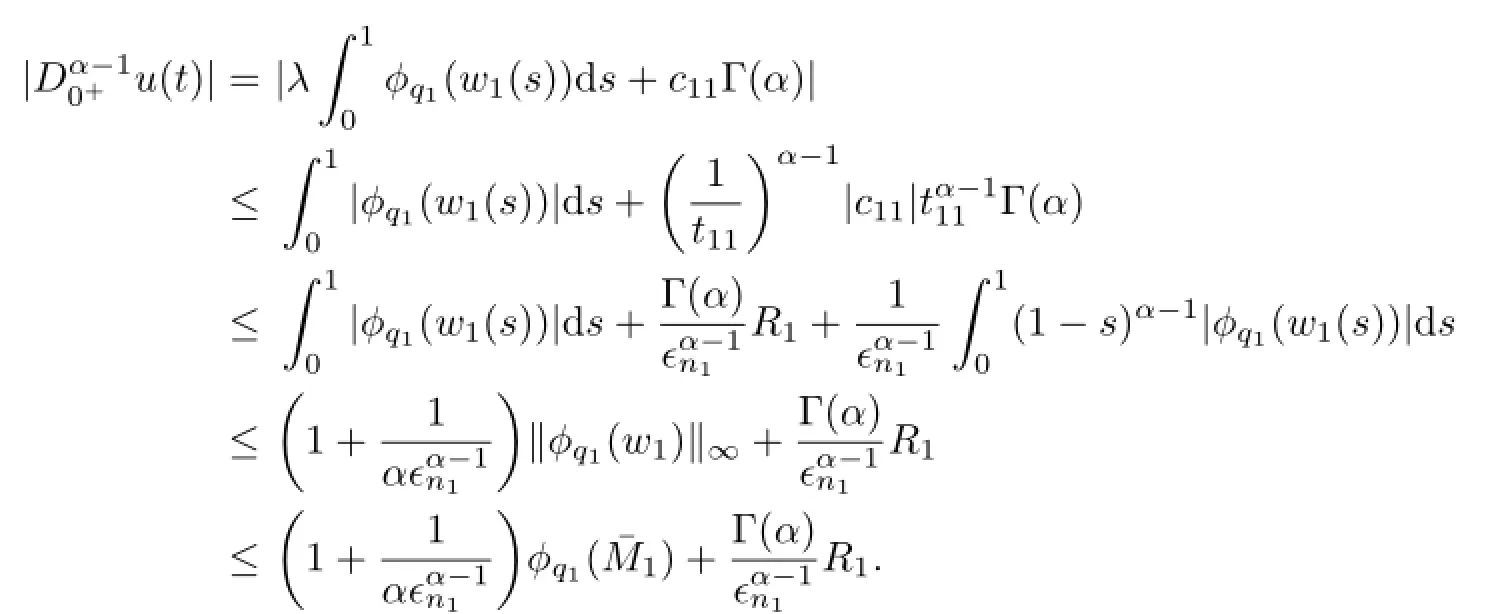
Likewisely,
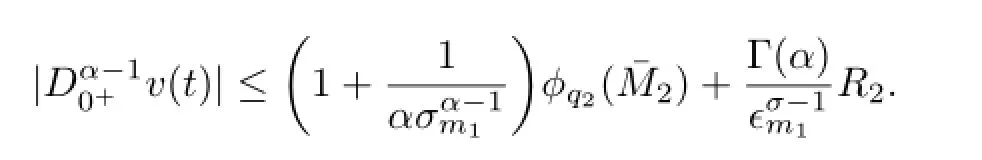
That is,
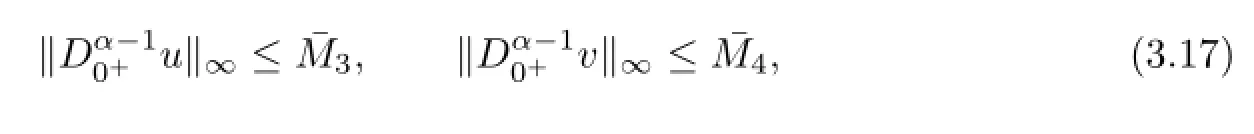
Since
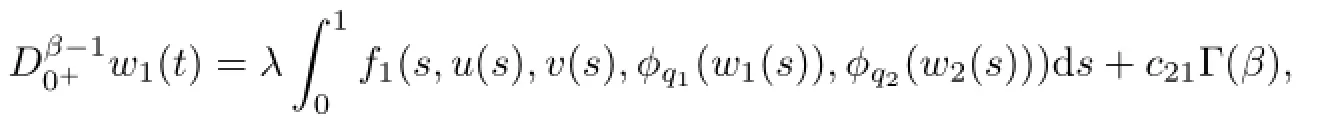
likewisely(3.15)and(3.17)obtained,and the condition(3.9b),we can know there exist constants,>0 such that
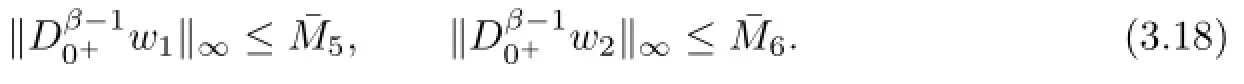
By(3.15)–(3.18),we have

where

Therefore,Ω1is bounded.The proof of Lemma 3.4 is completed.
Lemma 3.5Suppose that(H1),(H2)and(H5)hold.Then the set

is bounded in X.
Proof. For x=(u,v,w1,w2)T∈Ω2,we have
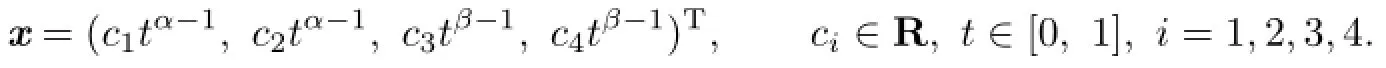
By Nx∈ImL,we know

By(H5),we know there exist constants ei>0 such that
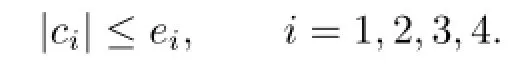
So
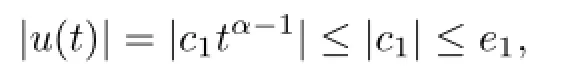
that is,
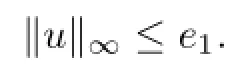
Likewisely,
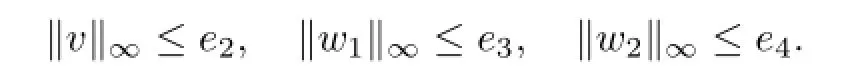
By Lemma 2.2,we can get
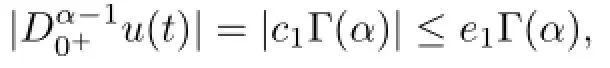
that is,
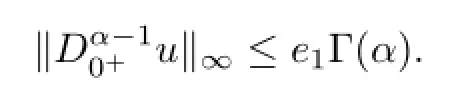
Likewisely,
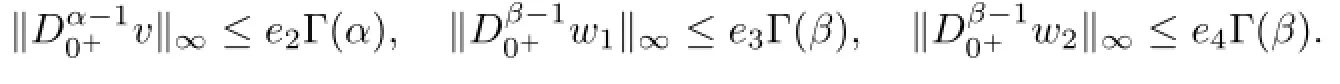
Thus
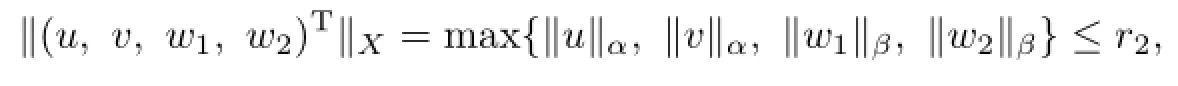
where
Therefore,Ω2is bounded.The proof of Lemma 3.5 is completed.
Lemma 3.6Suppose that(H1),(H2)and(H5)hold.Then the set
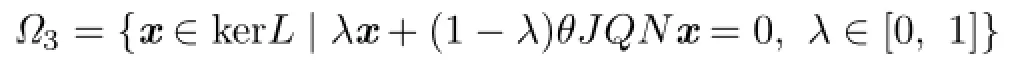
is bounded in X,where J:ImQ→kerL is a isomorphism given by

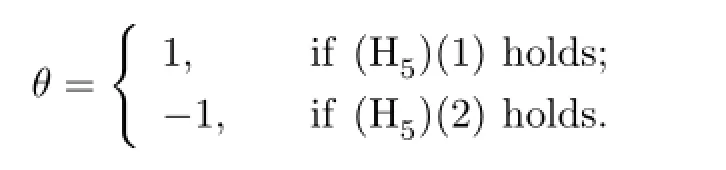
Proof. For x=(u,v,w1,w2)T∈kerL,(u,v,w1,w2)T=(c1tα−1,c2tα−1,c3tβ−1, c4tβ−1)T,ci∈R,t∈[0,1],i=1,2,3,4.There exists λ∈[0,1]such that
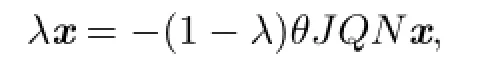
that is,
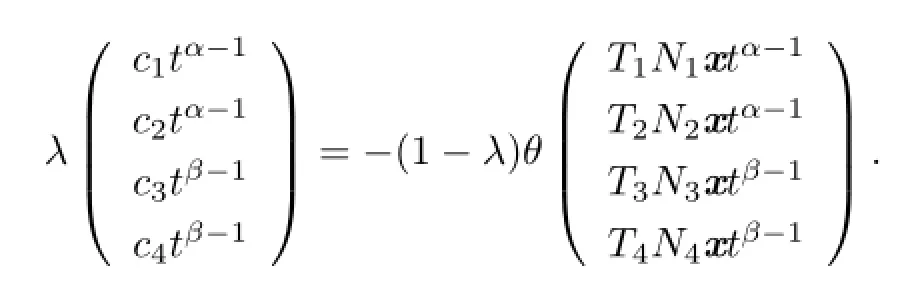
We get

If λ=0,by(H5),we get
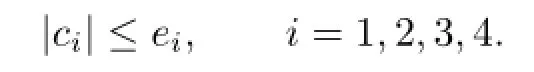
If λ=1,we get

For λ∈(0,1),one has
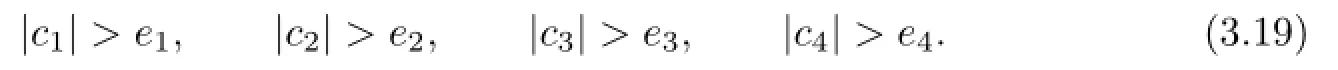
If at least one of the inequalities in(3.19)holds,we have that at least one of the following inequations holds:
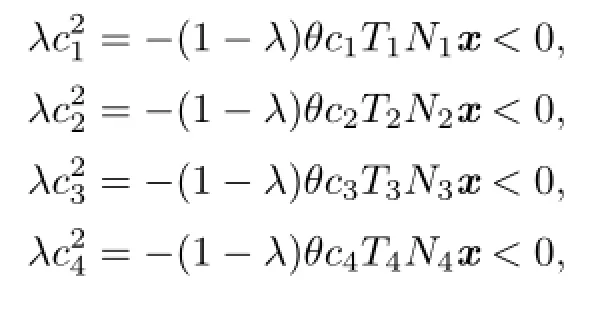
this is a contradiction.So,for λ∈[0,1],we get
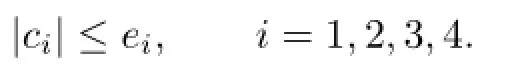
Similar to the proof of Lemma 3.5,we can get
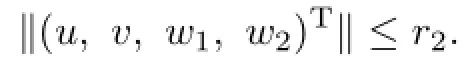
Therefore,we obtain Ω3is bounded.The proof of Lemma 3.6 is completed.
Theorem 3.1Suppose that(H1)–(H5)hold.Then the problem(1.1)has at least one solution in X.
Proof. Set

Obviously,Ω is a bounded open subset of X and Ω1∪Ω2∪Ω3⊂Ω.It follows from Lemmas 3.2 and 3.3 that L(defned by(2.2))is a Fredholm operator of index zero and N(defned by (2.3))is L-compact on.By Lemmas 3.4 and 3.5,we get that the following two conditions are satisfed:
(1)Lx/=λNx for every(x,λ)∈[(domLkerL)∩∂Ω]×(0,1);
(2)Nx/∈ImL for every x∈kerL∩∂Ω.
Next,we need only to prove
(3)deg(JQN|kerL,Ω∩kerL,0)/=0.
Take
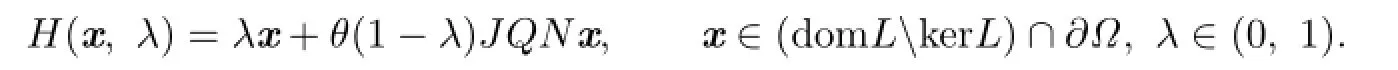
According to Lemma 3.6,we know
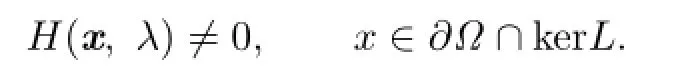
By the homotopy of degree,we have
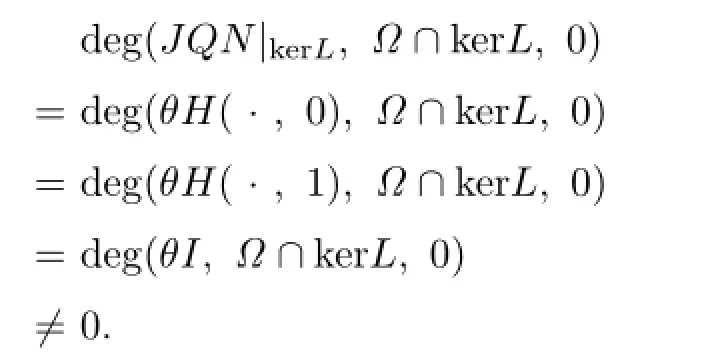
By Lemma 2.4,we can get that Lx=Nx has at least one solution on domL∩¯Ω.That is, (2.1)has at least one solution in X.Then we know(1.1)has at least one solution in X. The proof of Theorem 3.1 is completed.
4 Example
Let us consider the following coupled system of fractional p-Laplacian diferential equations at resonance
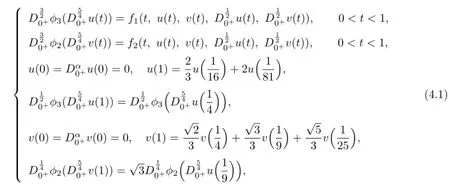
where
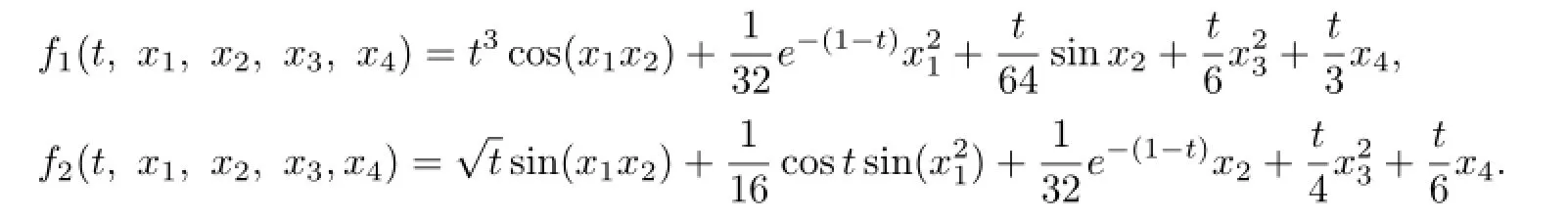
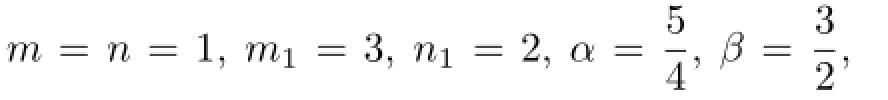
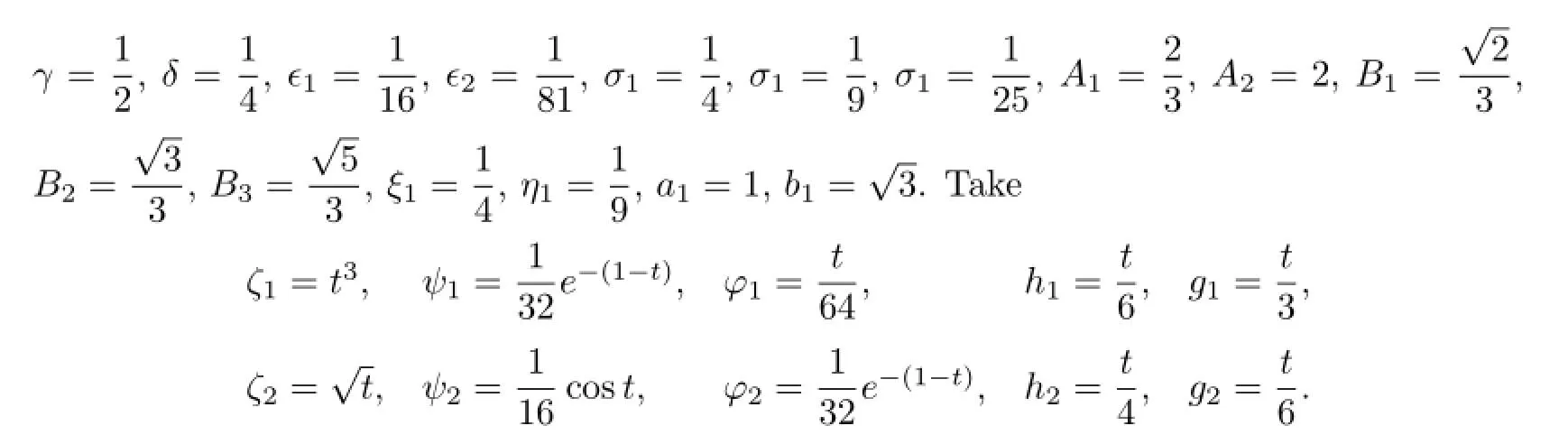
Then
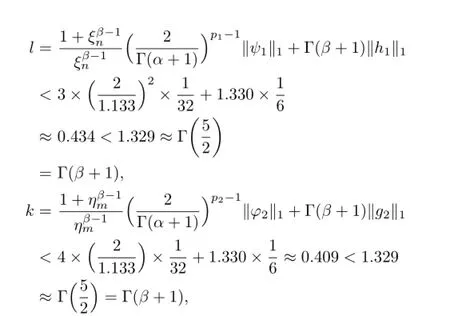
and
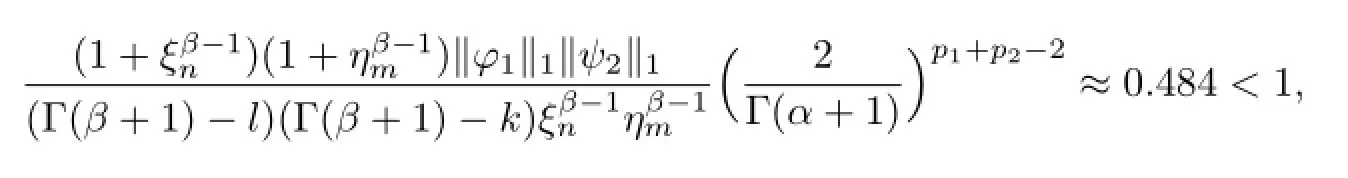

By simple calculation,we can get that(H1)–(H4)and(H5)(1)hold.By Theorem 3.1,we obtain that the problem(4.1)has at least one solution.
[1]Lian H,Pang H,Ge W.Solvability for second-order three-point boundary value problems at resonance on a half-line.J.Math.Anal.Appl.,2008,337:1171–1181.
[2]Zhang X,Feng M,Ge W.Existence result of second-order diferential equations with integral boundary conditions at resonance.J.Math.Anal.Appl.,2009,353:311–319.
[3]Kosmatov N.Multi-point boundary value problems on an unbounded domain at resonance. Nonlinear Anal.,2008,68:2158–2171.
[4]Du B,Hu X.A new continuation theorem for the existence of solutions to p-Lpalacian BVP at resonance.Appl.Math.Comput.,2009,208:172–176.
[5]Du Z,Lin X,Ge W.Some higher-order multi-point boundary value problem at resonance.J. Comput.Appl.Math.,2005,177:55–65.
[6]Xue C,Ge W.The existence of solutions for multi-point boundary value problem at resonance. Acta Math.Sinica,2005,48:281–290.
[7]Ma R.Existence results of a m-point boundary value problem at resonance.J.Math.Anal. Appl.,2004,294:147–157.
[8]Liu Y,Ge W.Solvability of nonlocal boundary value problems for ordinary diferential equations of higher order.Nonlinear Anal.,2004,57:435–458.
[9]Lu S,Ge W.On the existence of m-point boundary value problem at resonance for higher order diferential equation.J.Math.Anal.Appl.,2003,287:522–539.
[10]Liu B.Solvability of multi-point boundary value problem at resonance(II).Appl.Math.Comput.,2003,136:353–377.
[11]Igor Podlubny.Fractional Diferential Equations.New York-London:Academic Press,1999.
[12]Miller K S,Ross B.An Introduction to the Fractional Calculus and Fractional Diferential Equations.New York:Wiley,1993.
[13]Yang A,Ge W.Positive solutions for boundary value problems of N-dimension nonlinear fractional diferential system.Bound.Value Probl.,2008,437–453.
[14]Su X.Boundary value problem for a coupled system of nonlinear fractional diferential equations.Appl.Math.Lett.,2009,22:64–69.
[15]Kosmatov N.A boundary value problem of fractional order at resonance.Elec.J.Diferential Equations,2010,135(1),1–10.
[16]Jiang W H.Solvability for a coupled system of fractional diferential equations at resonance. Nonlinear Anal.,2012,13:2285–2292.
[17]Leibenson L S.General Problem of the Movement of a Compressible Fluid in a Porous Medium (in Russian).Moskva:Izvestiia Akademii Nauk Kirgizsko SSSR,1983:7–10.
[18]Chen T Y,Liu W B,Hu Z G.A boundary value problem for fractional diferential equation with p-Laplacian operator at resonance.Nonlinear.Anal.,2012,75:3210–3217.
[19]Mawhin J.Topological degree methods in nonlinear boundary value problems.in:CBMS Regional Conference Series in Mathematics,American Mathematical Society,Providence,RI, 1979.
[20]Jiang J Q,Liu L S,Wu Y H.Positive solutions for p-Laplacian fourth-order diferential system with integral boundary conditions.Discrete Dyn.Nat.Soc..2012,Article ID 293734,19 pages.
A
1674-5647(2017)01-0033-20
10.13447/j.1674-5647.2017.01.05
Received date:April 13,2015.
Foundation item:The Key NSF(KJ2015A196)of Anhui Higher Education and the Young Foundation (2015QN19)of Hefei Normal University.
*Corresponding author.
E-mail address:zhouhui0309@126.com(Zhou H),zhouzf12@126.com(Zhou Z F).
2010 MR subject classifcation:26A33,34B15
 Communications in Mathematical Research2017年1期
Communications in Mathematical Research2017年1期
- Communications in Mathematical Research的其它文章
- L2-harmonic 1-forms on Complete Manifolds
- Trees with Given Diameter Minimizing the Augmented Zagreb Index and Maximizing the ABC Index
- Bonnesen-style Isoperimetric Inequalities of an n-simplex
- 2N+1-soliton Solutions of Boussinesq-Burgers Equation
- The Value Distribution and Normality Criteria of a Class of Meromorphic Functions
- Multiplicative Jordan Decomposition in Integral Group Ring of Group K8×C5
