2N+1-soliton Solutions of Boussinesq-Burgers Equation
LI QIAN,XIA TIE-CHENGAND CHEN DENG-YUAN
(1.Department of Mathematics,Shanghai University,Shanghai,200444)
(2.College of Science,Zhengzhou Institute of Aeronautics Industry Management, Zhengzhou,450005)
2N+1-soliton Solutions of Boussinesq-Burgers Equation
LI QIAN1,2,XIA TIE-CHENG1,*AND CHEN DENG-YUAN1
(1.Department of Mathematics,Shanghai University,Shanghai,200444)
(2.College of Science,Zhengzhou Institute of Aeronautics Industry Management, Zhengzhou,450005)
Communicated by Wang Chun-peng
2N+1-soliton solutions of Boussinesq-Burgers equation are obtained by using the Hirota bilinear derivative method and the perturbation technique.Further,we give the graphs of corresponding three-and fve-soliton solutions.
Boussinesq-Burgers equation,Hirota bilinear derivative method,2N+1-soliton solution
1 Introduction
The research of soliton equations is one of the most important subjects in the feld of nonlinear science.However,due to their high nonlinearity,it is very difcult to solve them. Up to now,several systematic methods has been developed to obtain explicit solutions of soliton equations,for instance,the inverse scattering transformation(see[1]–[2]),the Hirota bilinear derivative transformation(see[3]–[4]),the dressing method(see[5]),the B¨acklund and the Darboux transformation(see[6]–[8]),the algebra-geometric method(see [9]–[10]),the nonlinearization approach of eigenvalue problems or Lax pairs(see[11]–[12]), etc.Among the various methods,the Hirota bilinear derivative transformation is a powerful tool to generate exact solutions of the nonlinear evolution equations.And this method has the advantage of being applicable directly upon the nonlinear evolution equations.The key of the method is to transform the equation under consideration into the bilinear derivativeequation through the dependent variable transformation.Then N-soliton solutions with exponential function form can be obtained with the help of the perturbation expansion and truncation technique.
As is well known,classical Boussinesq-Burgers(CBB)spectral problem is
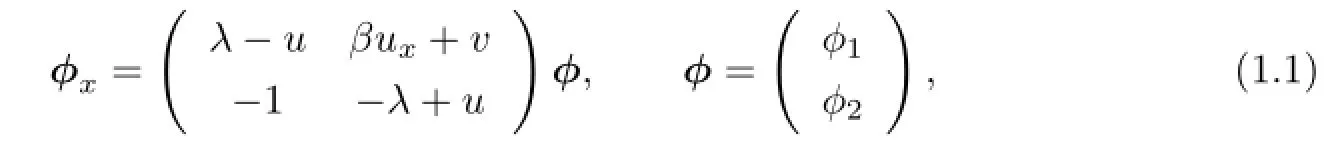
where λ is a spectral parameter,β is a constant,u and v are two potentials.The spectral problem was initially introduced by Date[13].Geng and Wu[14]constructed the fnite-band solutions of evolution equations associated with the spectral problem(1.1),and the CBB equation is given as follows:
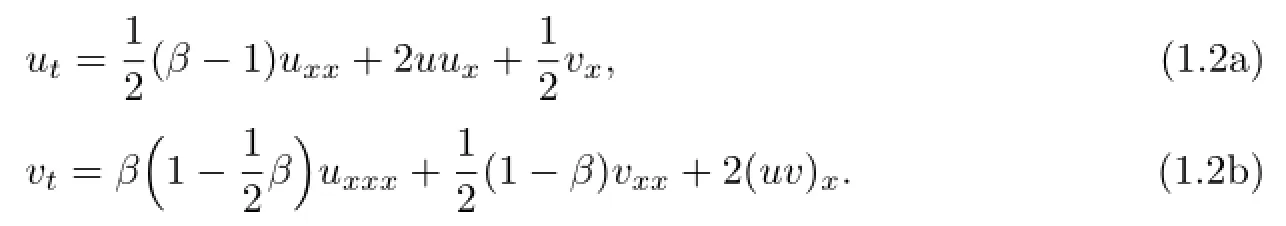
Xu[15]discussed its Darboux transformation and give some explicit solutions.For the special case of the spectral problem(1.1)with β=0,this has been studied by Li[16].
In the present paper,we would consider the special case of(1.2)(β=1),which is Boussinesq-Burgers equation as follows.

Based on Hirota bilinear derivative transformation,we obtain three-soliton solutions,fvesoliton solutions and 2N+1-soliton solutions of(1.3).To our knowledge,these solutions are new ones.
2 Bilinear Equation and 2N+1-soliton Solutions
In this section,frstly,we introduce the logarithm transformations of dependent variables u and v as
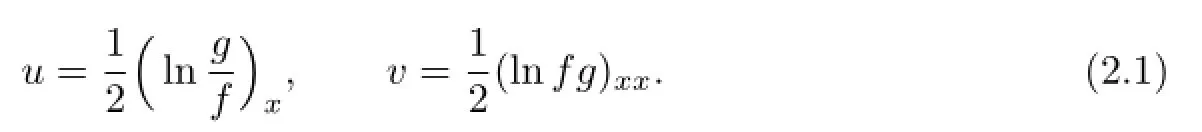
Substituting transformations(2.1)into(1.3)and integrating it once with respect to x,(1.1) can be transformed into the following bilinear equations:

where D is the well-known Hirota’s bilinear operator that defned as

In what follows,we would construct multi-soliton solutions of(1.3)based on the perturbation method.We expand f,g as the power series in a small parameter ε that are diferent from the usual.

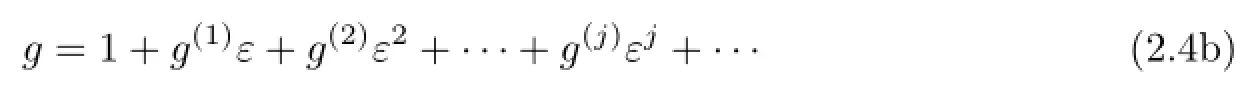
Substituting(2.4)into(2.2)and collecting terms of each order of ε yields the following recursion relations
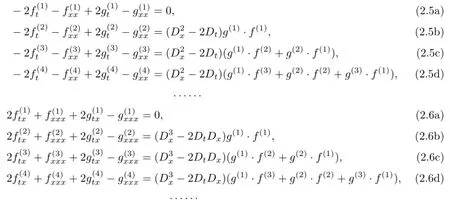
(1)Three-soliton solutions.Integrating(2.6a)once with respect to x and selecting the constant of integration to be zero,we have
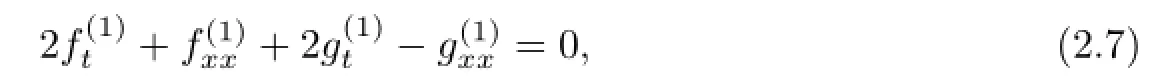
(2.5a)plus(2.7),we get
Then we can select a special solution
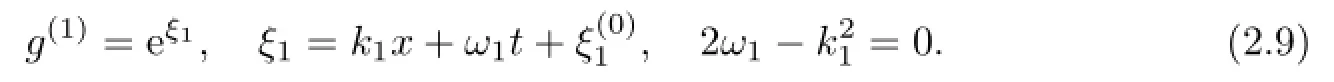
Similarly,(2.7)minus(2.5a),we arrive at
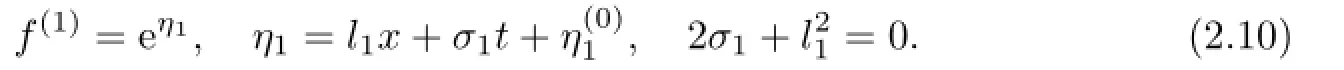
Substituting g(1)=eξ1,f(1)=eη1into(2.5b)and(2.6b),after a direct calculation,we have

Putting(2.9),(2.10),(2.11)into(2.5c)and(2.6c),they return to(2.5a)and(2.6a)by using superscript(1.3)instead of(1.1),then we can choose
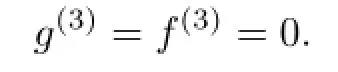
Take
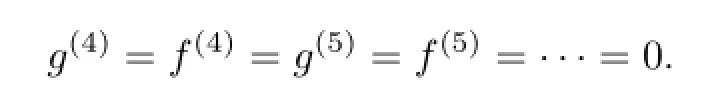
Select ε=1.Thus,f and g are truncated as

eθ13=(k1+l1)−2.With the help of(2.1),we get a three-soliton solutions of(1.3)

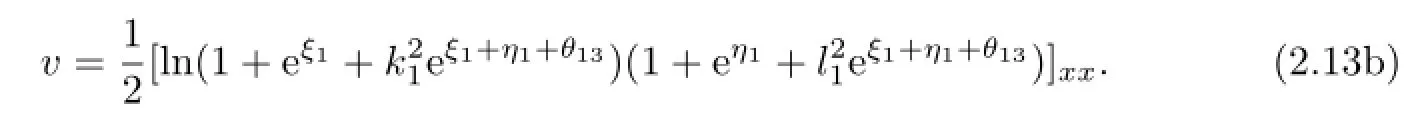
The corresponding graphs are shown in Fig.2.1.
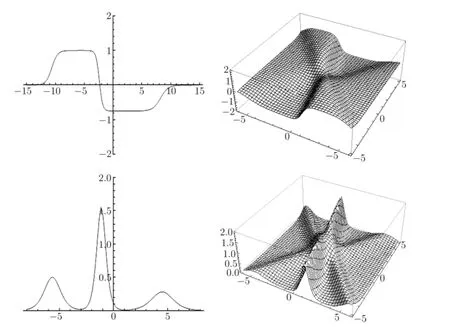
Fig.2.1 The shape of the three-soliton solutions of(2.13)with k1=2,l1=1.5,
(2)Five-soliton solutions.Obviously,
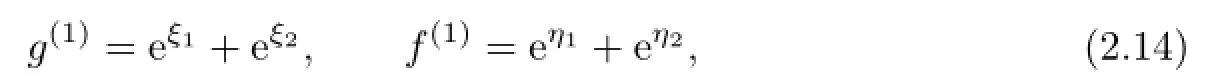
with
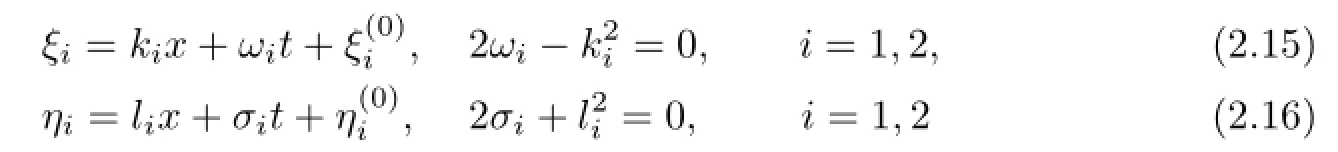
are still solutions of(2.5a)and(2.6a).
Substituting(2.14)into(2.5b)and(2.6b),and integrating(2.6b)once with respect to x and selecting the constant of integration to be zero,we can get
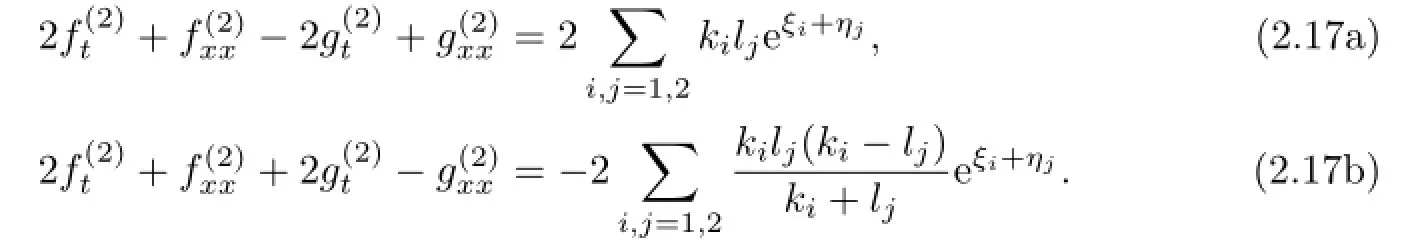
Letting(2.17b)minus or plus(2.17a),we can obtain
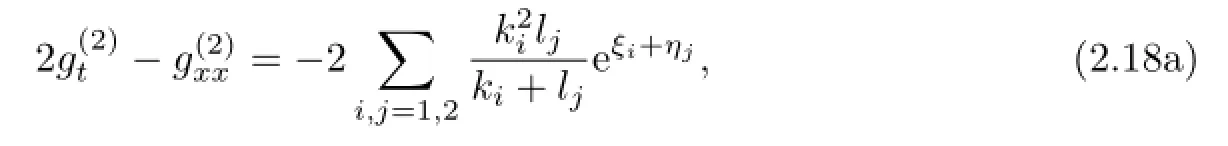
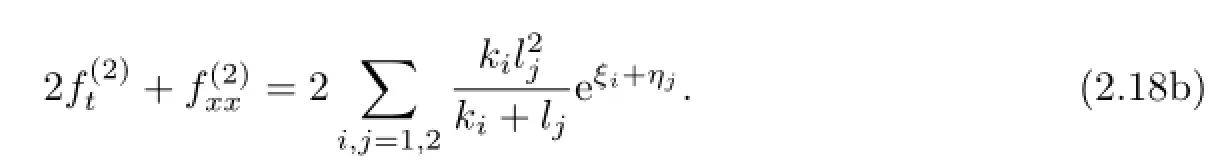
Then the linear equations(2.18)have a special solution
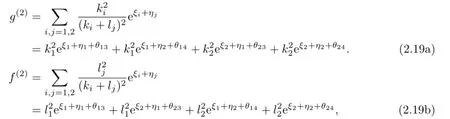
where eθj(s+2)=(kj+ls)−2(j,s=1,2).
Similarly,utilizing(2.14)and(2.19),from(2.5c)and(2.6c)through complicated calculation,we get
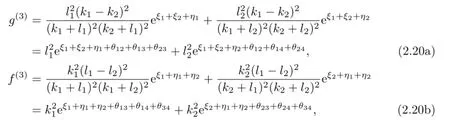
where eθ12=(k1−k2)2,eθ34=(l1−l2)2.
Substituting(2.14),(2.19)and(2.20)into(2.5c)and(2.6c),after tedious calculation with the help of the maple,we arrive at
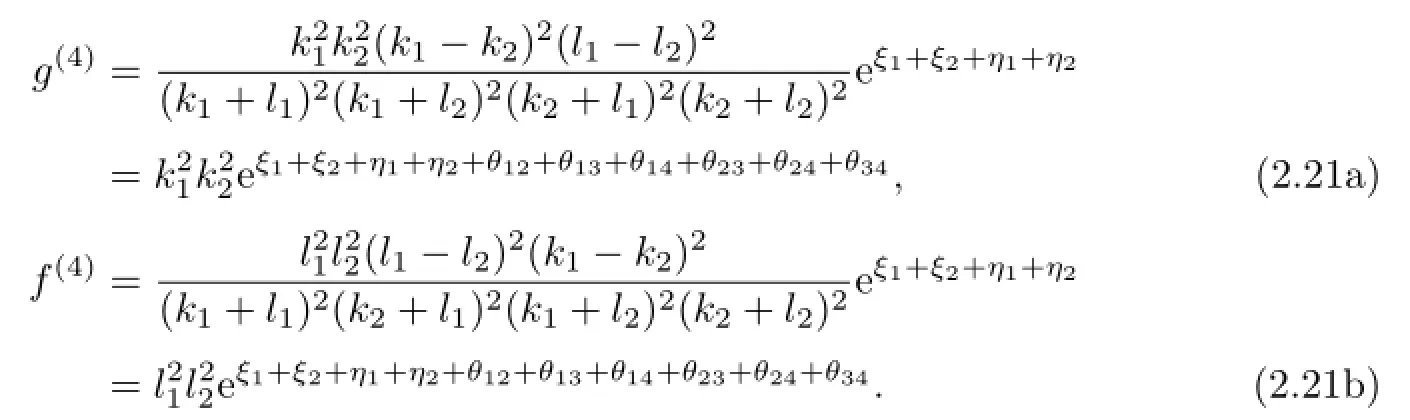
Putting(2.14),(2.19)–(2.21)into(2.5d)and(2.6d),we can obtain a special solution

Take g(6)=f(6)=g(7)=f(7)=···=0 and ε=1.Then the functions f,g are reduced to
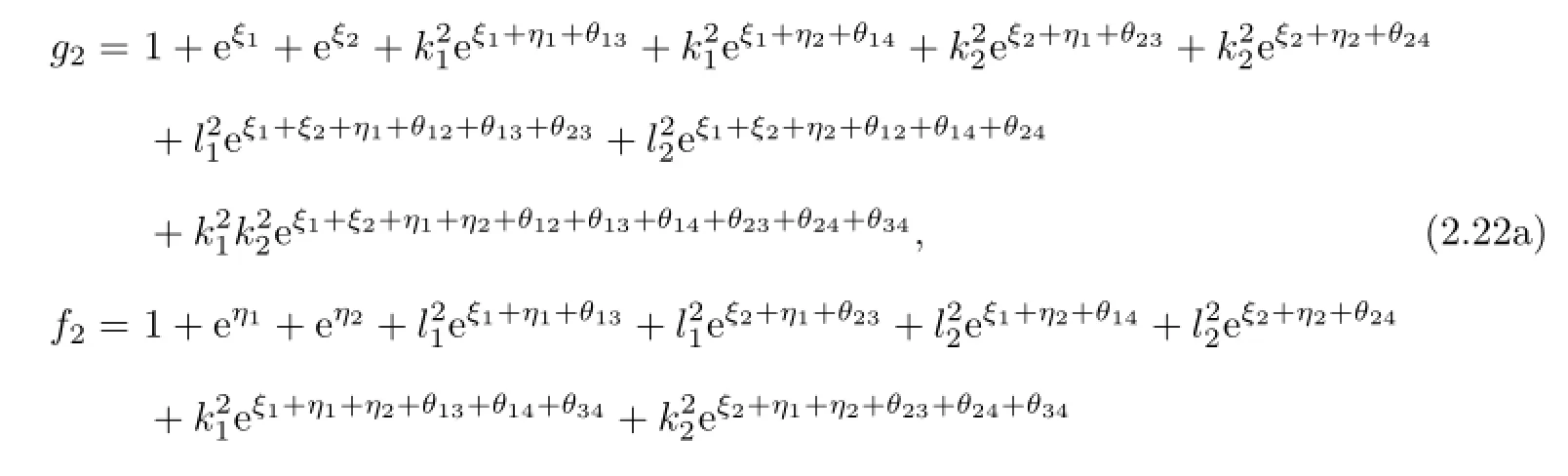
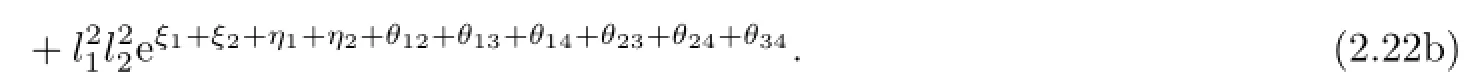
Substituting(2.14),(2.19)–(2.21)into(2.1),we work out a fve-soliton solutions of the Boussinesq-Burgers equation(1.3).The corresponding graphs are shown in Fig.2.2.
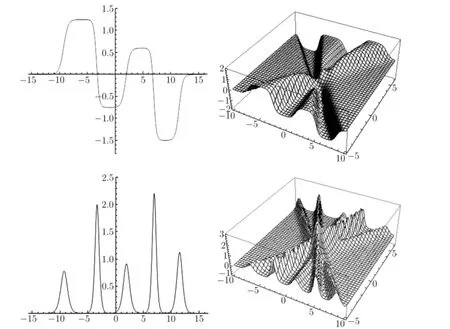
Fig.2.2 The shape of the fve-soliton solutions of(2.13)with k1=1.5,l1=1.2,k2=3, l2=2.5,=2,=2,=1,=4
(3)2N+1-soliton solutions.In general,we have
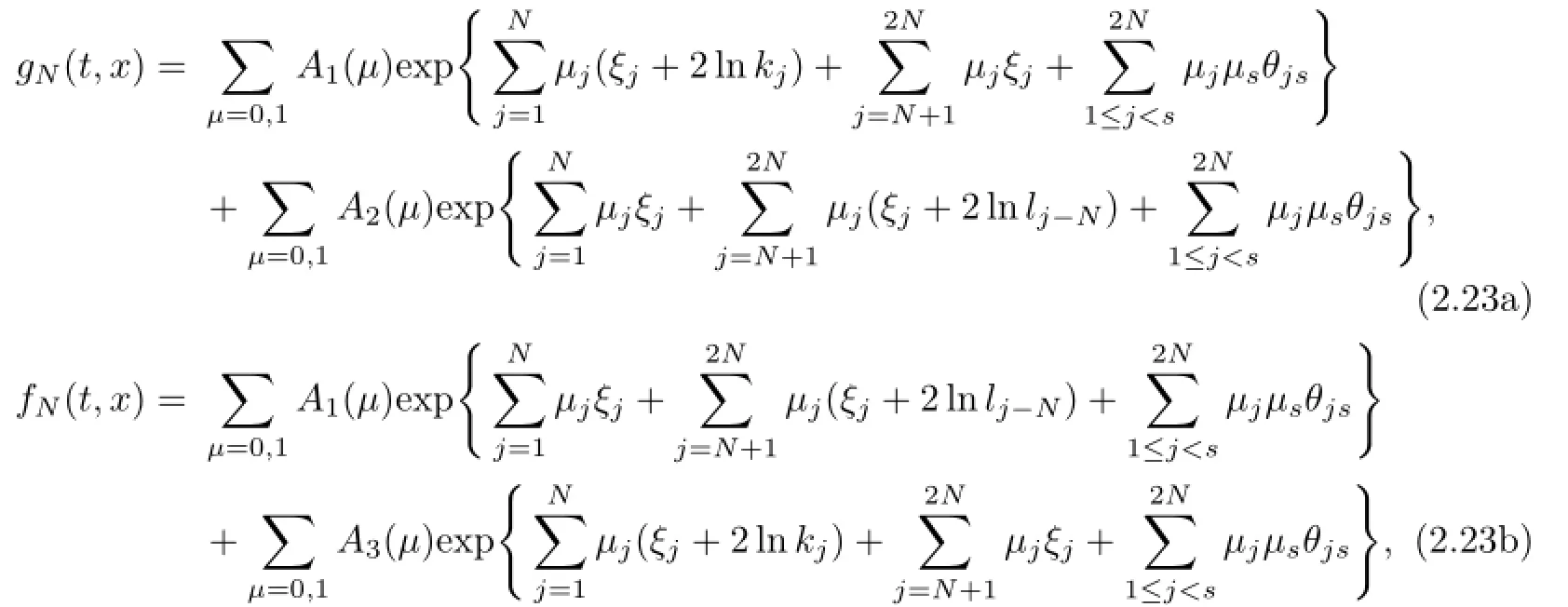
where
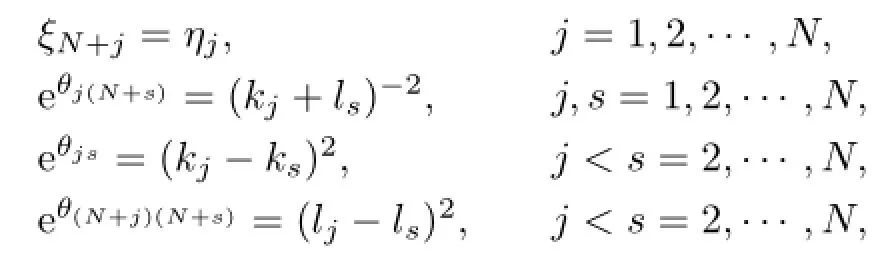
the notations A1,A2and A3stand for all possible combinations ofµj=0,1(j=1,2,···,N) and satisfy the conditions
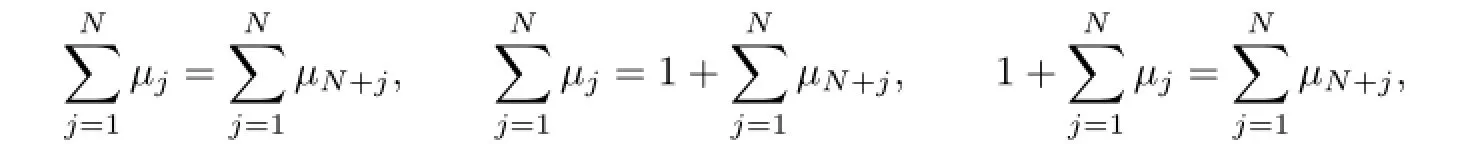
respectively.Substituting(2.23)into(2.1),we arrive at 2N+1-soliton solutions of the Boussinesq-Burgers equation(1.3).And they are new soliton solutions of(1.3).
3 Conclusions
In the present paper,we obtain 2N+1-soliton solutions for Boussinesq-Burgers equation based on Hirota bilinear derivative method and the perturbation technique.However, whether the Boussinesq-Burgers equation have Wronskian determinant form of solution remains an open problem,and we will discuss it elsewhere.
[1]Ablowitz M J,Clarkson P A.Solitons,Nonlinear Evolution Equations and Inverse Scattering. Cambridge:Cambridge University Press,1991.
[2]Ablowitz M J,Segur H.Solitons and the Inverse Scattering Transform.Philadelphia,PA: SIAM,1981.
[3]Hirota R.Exact N-soliton solution of a nonlinear lumped self-daul network equation.J.Phys. Soc.Japan,1973,35:289–294.
[4]Wu J P,Geng X G,Zhang X L.N-soliton solution of a generalized Hirota-Satsuma coupled KdV equation and its reduction.Chin.Phys.Lett.,2009,26:020202.
[5]Novikov S P,Manakov S V,Pitaevskii L P,Zakharov V E.Theory of Solitons,the Inverse Scattering Methods.New York:Consultants Bureau,1984.
[6]Lamb G L.Elements of Soliton Theory.New York:Wiley,1980.
[7]Matveev V B,Salle M A.Darboux Transformations and Solitons.Berlin:Springer,1991.
[8]Pickering A,Zhu Z N.Darboux-B¨acklund transformation and explicit solutions to a hybrid lattice of the relativistic Toda lattice and the modifed Toda lattice.Phys.Lett.A,2014,378: 1510–1513.
[9]Belokolos E D,Bobenko A I,Enolskii V Z,Its A R.Algebro-geometric Approach to Nonlinear Integrable Equations.Berlin:Springer,1994.
[10]Geng X G,Wu L H,He G L.Quasi-periodic solutions of the Kaup-Kupershmidt hierarchy.J. Nonlinear Sci.,2013,23:527–555.
[11]Cao C W,Wu Y T,Geng X G.Relation between the Kadomtsev-petviashvili equation and the confocal involutive system.J.Math.Phys.,1999,40:3948–3970.
[12]Geng X G,Cao C W.Decomposition of the(2+1)-dimensional Gardner equation and its quasi-periodic solutions.Nonlinearity,2001,14:1433–1452.
[13]Date E.On quasi-periodic solutions of the feld equation of the classical massive thirring model. Progr.Theoret.Phys.,1978,59:265–273.
[14]Geng X G,Wu Y T.Finite-band solutions of the classical Boussinesq-Burgers equations.J. Math.Phys.,1999,40:2971–2982.
[15]Xu R.Darboux transformation and soliton solutions of classical Boussinesq-Burgers equation. Commun.Theor.Phys.,2008,50:579–582.
[16]Li Y S,Ma W X,Zhang J E.Darboux transformations of classical Boussinesq system and its new solutions.Phys.Lett.A.,2000,275:60–66.
A
1674-5647(2017)01-0026-07
10.13447/j.1674-5647.2017.01.04
Received date:May 11,2015.
Foundation item:The NSF(11271008)of China,the First-class Discipline of University in Shanghai and the Shanghai Univ.Leading Academic Discipline Project(A.13-0101-12-004).
*Corresponding author.
E-mail address:liq689@163.com(Li Q),xiatc@shu.edu.cn(Xia T C).
2010 MR subject classifcation:35Q51,35Q58
 Communications in Mathematical Research2017年1期
Communications in Mathematical Research2017年1期
- Communications in Mathematical Research的其它文章
- L2-harmonic 1-forms on Complete Manifolds
- Trees with Given Diameter Minimizing the Augmented Zagreb Index and Maximizing the ABC Index
- Bonnesen-style Isoperimetric Inequalities of an n-simplex
- The Value Distribution and Normality Criteria of a Class of Meromorphic Functions
- Multiplicative Jordan Decomposition in Integral Group Ring of Group K8×C5
- Endpoint Estimates for Commutators of Fractional Integrals Associated to Operators with Heat Kernel Bounds
