Multiplicative Jordan Decomposition in Integral Group Ring of Group K8×C5
WANG XIU-LANAND ZHOU QING-XIA
(1.College of Basic Science,Tianjin Agricultural University,Tianjin,300384)
(2.School of Science,Tianjin University of Technology,Tianjin,300384)
Multiplicative Jordan Decomposition in Integral Group Ring of Group K8×C5
WANG XIU-LAN1AND ZHOU QING-XIA2
(1.College of Basic Science,Tianjin Agricultural University,Tianjin,300384)
(2.School of Science,Tianjin University of Technology,Tianjin,300384)
Communicated by Du Xian-kun
In this article,we present the multiplicative Jordan decomposition in integral group ring of group K8×C5,where K8is the quaternion group of order 8. Thus,we give a positive answer to the question raised by Hales A W,Passi I B S and Wilson L E in the paper“The multiplicative Jordan decomposition in group rings II. J.Algebra,2007,316:109–132”.
integral group ring,Jordan decomposition,semisimple element,nilpotent element
1 Introduction
Let G be a fnite group andQthe feld of rational numbers.Then every element α in the group algebraQG has a unique additive Jordan decomposition α=αs+αnwith αs,αn∈QG,αsis semisimple,αnis nilpotent and αsαn=αnαs.Recall that an element α∈FG is said to be semisimple if the minimal polynomial m(X)of α over F does not have repeated roots in the algebraic closureof F with F a feld of characteristic 0.Furthermore, if α is a unit inQG,then so is αs,and α has a unique multiplicative Jordan decomposition α=αsαuwithαnunipotent and αsαu=αuαs.But,when α∈ZG,the integral group ring over G,the semisimple component αsdoes not always lie inZG.The integral group ringZG is said to have the additive Jordan decomposition(or AJD for short)property if αs∈ZG(and hence αn∈ZG)for every α∈ZG,and to have the multiplicative Jordan decomposition(or MJD for short)property if αsand αu∈ZG for every unit α∈ZG.IfZG has the AJD property,then in fact it also has the MJD property.Therefore,to considerthe groups G such thatZG has the MJD property,we need to consider the case that ifZG has the AJD property.
The fnite groups G whose integral group ringZG has the AJD property are completely classifed in[1]and[2].If G is abelian or a Hamiltonian 2-group,then every element ofQG is semisimple and consequentlyZG trivially has the MJD property.In[3],the necessary conditions for a fnite group G whose integral group ringZG has the MJD property are given as follows:
Theorem 1.1([3],Theorem 29) Let G be a fnite group such thatZG has MJD.Then one of the following holds:
(1)G is either abelian or of the form K8×E×H,where E is an elementary abelian 2-group and H is abelian of odd order so that 2 has odd multiplicative order mod|H|.(Such G have AJD and hence MJD for trivial reasons,sinceQG contains no nilpotent.)
(2)G has order 2a3bfor some nonnegative integers a,b.
(3)G=K8×Cpfor some prime p≥5 so that 2 has even multiplicative order mod p.
(4)G is the split extension of Cp(p≥5)by a cyclic group〈g〉of order 2kor 3kfor some k≥1,and g2or g3acts trivially on Cp.
To completely classify the fnite groups G such thatZG has the MJD property,we need only to investigate the four cases listed in Theorem 1.1.It has been shown that the integral group rings of abelian groups have the AJD property in[2],and so the MJD property.For the fnite non-abelian 2-groups whose integral group rings possess the MJD property,there are two groups of order 8(see[4]),fve groups of order 16(see[5]),four groups of order 32 and only the Hamiltonian groups of larger order(see[3]for details).Liu and Passman[6]showed that for the fnite non-abelian 3-groups whose integral group rings have the MJD property,there are two groups of order 27 and at most three other groups(all of order 81) for larger order.Liu and Passman[7]also proved that there are precisely three non-abelian 2,3-groups of order divisible by 6,withZG satisfying MJD.
SinceQ(K8×Cp)has no nilpotent elements for p a prime such that 2 has odd multiplicative order mod p,the integral group ringZ(K8×Cp)trivially has the MJD property. When p is some odd prime such that 2 has even multiplicative order mod p,Hales et al.[3]claimed that“We do not know if these groups ever have MJD for their integral group rings. The frst example to investigate would beZ(K8×C5).”
In this article,we present the multiplicative Jordan decomposition in integral group ring of group K8×C5,where K8is the quaternion group of order 8.Thus,we give a positive answer to the question raised by Hales et al.in[3].
2 The AJD for the Units of Z(K8×Cp)in Q(K8×Cp)
Lemma 2.1[1]If α inQG is central and β inQG is semisimple,then α+β is semisimple.
Let Cp=〈t〉be a cyclic group of order p and ζ a primitive pth root of unity.Let U1(ZCp) and U1(Z[ζ])denote the sets of 1-units forZCpandZ[ζ],separately.We consider the map

If u=∑citi∈U1(ZCp),then u(1,∑ciζi)with∑ci=1 and∑ciζi∈U1(Z[ζ]). Conversely,given any∑biζi∈U1(Z[ζ])with∑bi=1,it is easy to see that u=∑bitilies in U1(ZCp)and u(1,∑biζi).Thus,U1(ZCp)U1(Z[ζ]).
Theorem 2.1Every non-semisimple unit ofZ(K8×Cp)can be written as a sum of a semisimple unit and a nilpotent element inQ(K8×Cp),where
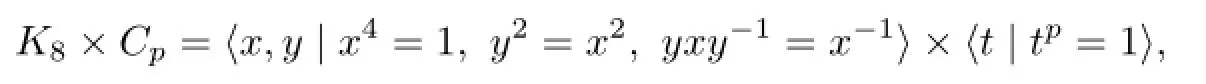
and p is some prime such that 2 has even multiplicative order mod p.
Proof. It is well known that K8×Cphas 5p conjugacy classes,then there are 5p irreducible complex representations,in which 4p have degree 1 and p have degree 2.The 5p irreducible complex representations of K8×Cpare given by
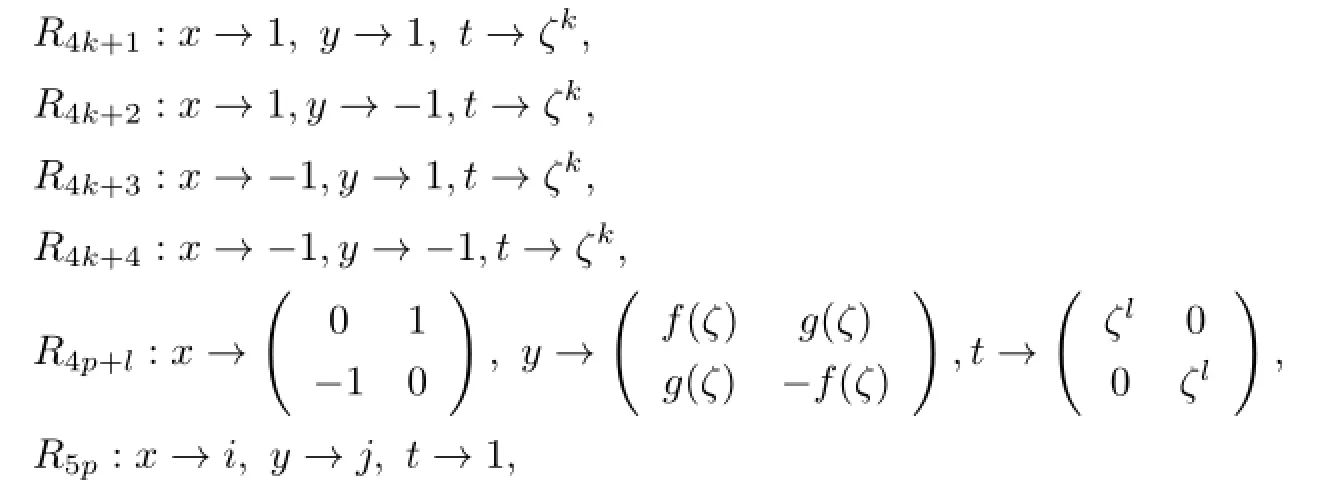
where 0≤k≤p−1,1≤l≤p−1,and the polynomials f and g satisfy
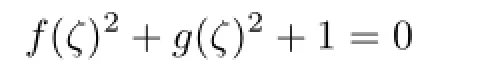
since p is some prime such that 2 has even multiplicative order mod p.
We can see that Ri(1≤i≤8),R4p+1and R5pare the irreducible rational representations and the Wedderburn decomposition of the rational group algebraQ(K8×Cp)is given as:
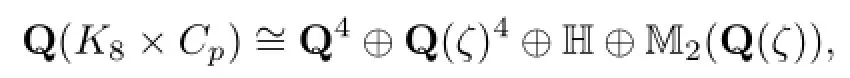
where H is the rational quaternion algebra and M2(Q(ζ))is the set of 2×2 matrices with entries inQ(ζ).
Suppose that
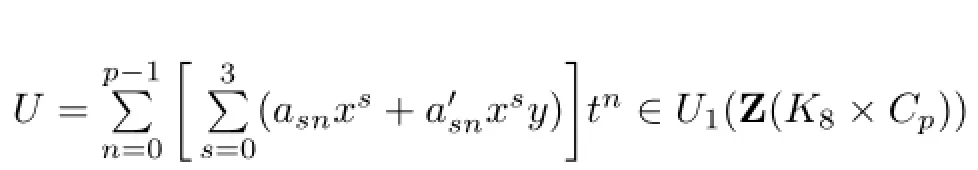
is not semisimple.Write
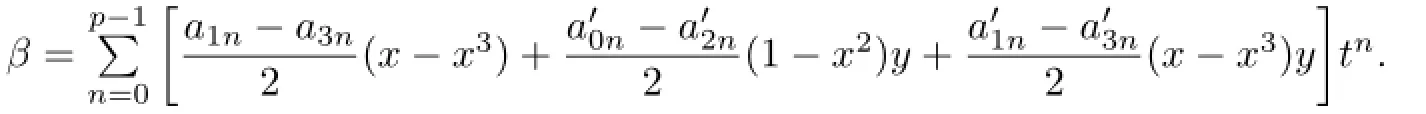
Then
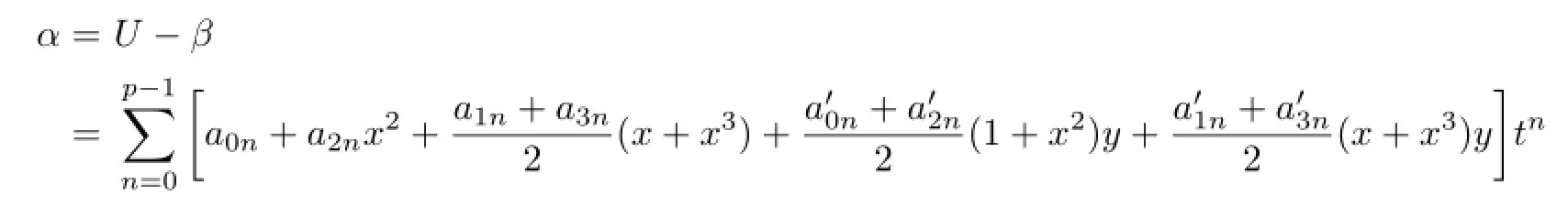
is central,and hence,is semisimple.In order to show that U=α+β is the decomposition with α semisimple and β nilpotent inQ(K8×Cp),it is sufcient to show that the image of β in every Wedderburn component is nilpotent.
Write
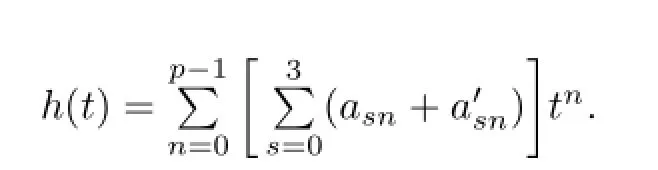
Since

it is easy to see that h(t)∈U1(ZCp),and hence
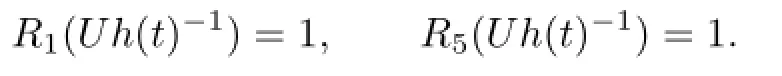
Replacing U by Uh(t)−1,we can assume

and then
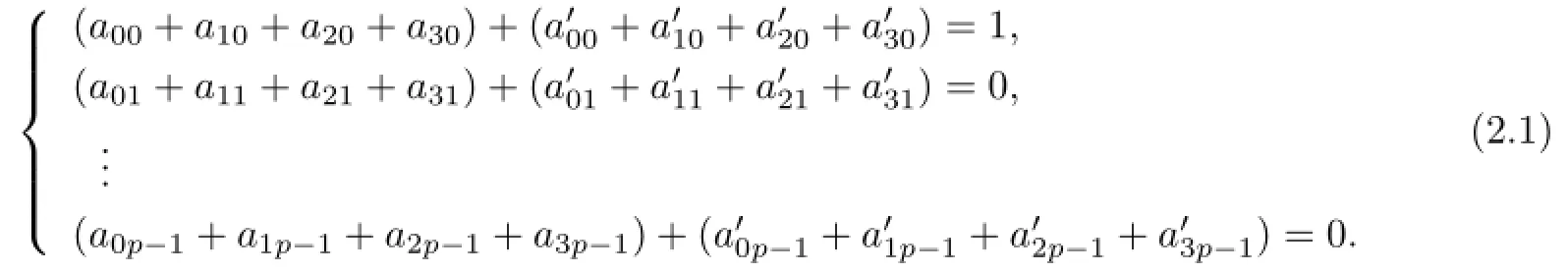
Furthermore,
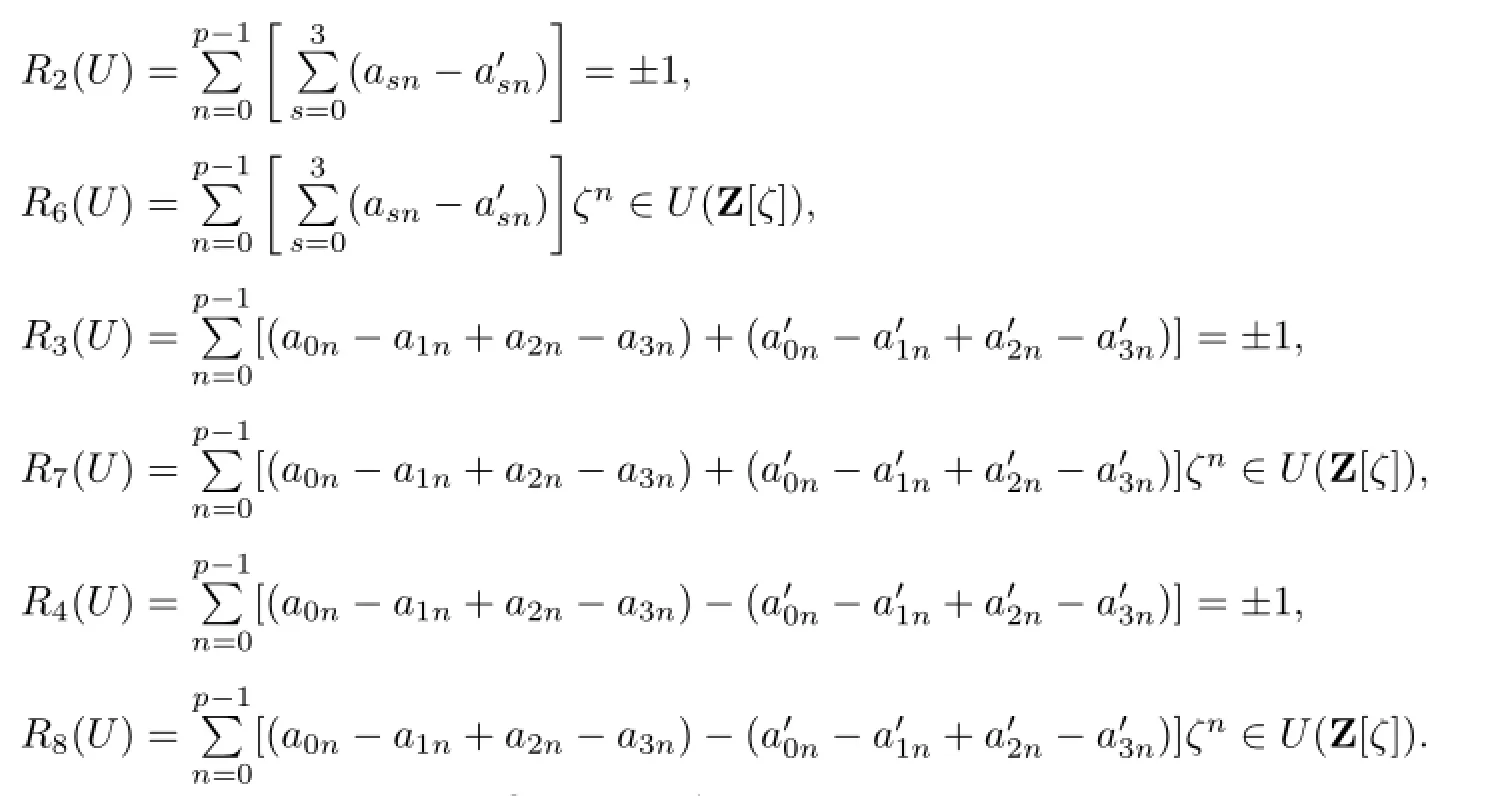
By(2.1),all the coefcients of ζ,ζ2,···,ζp−1in R6(U),R7(U)and R8(U)are even.Because of U∈U1(Z(K8×Cp)),we also have
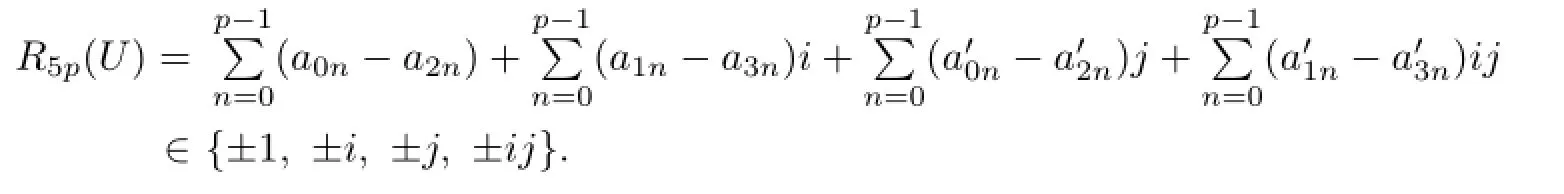
It follows that either
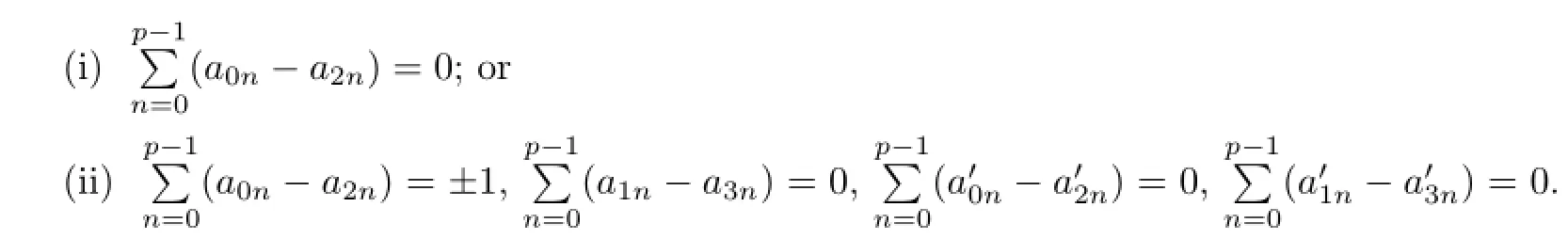
Then,by(i)and(ii),
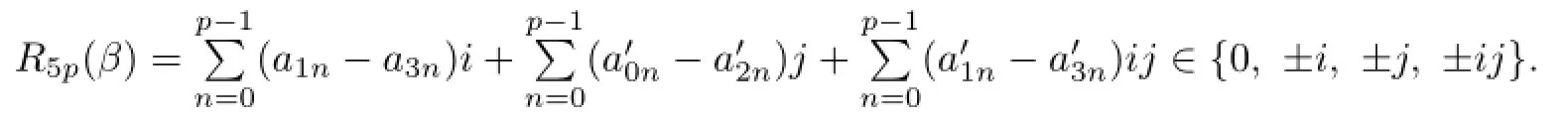
Moreover,

where
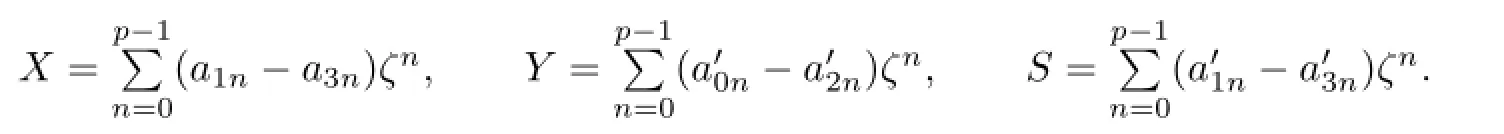
Note that
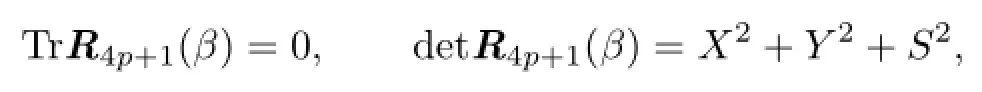
where“Tr”and“det”denote trace and determinant of the matrix R4p+1(β),separately.
Case 1.If detR4p+1(β)/=0,associate with TrR4p+1(β)=0,then R4p+1(β)is semisimple.Moreover,Ri(β)=0(1≤i≤8)and R5p(β)∈{0,±i,±j,±ij}are also semisimple. It follows that β is a semisimple element,and then U=α+β is also semisimple by Lemma 2.1,which is a contradiction to the assumption that U is not semisimple.
Case 2.If detR4p+1(β)=0,associate with TrR4p+1(β)=0,then R4p+1(β)is nilpotent.
Immediately,we have
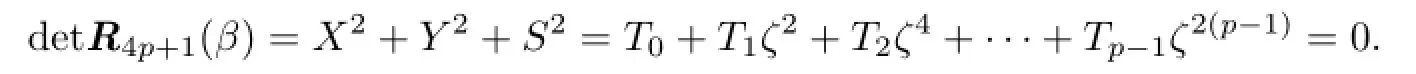
If(i)holds,then
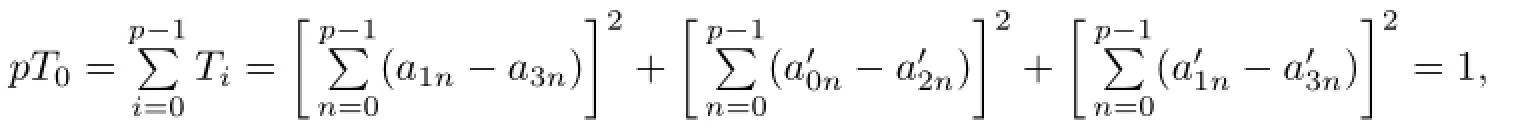
which is impossible since T0∈Z.Thus,(ii)holds and
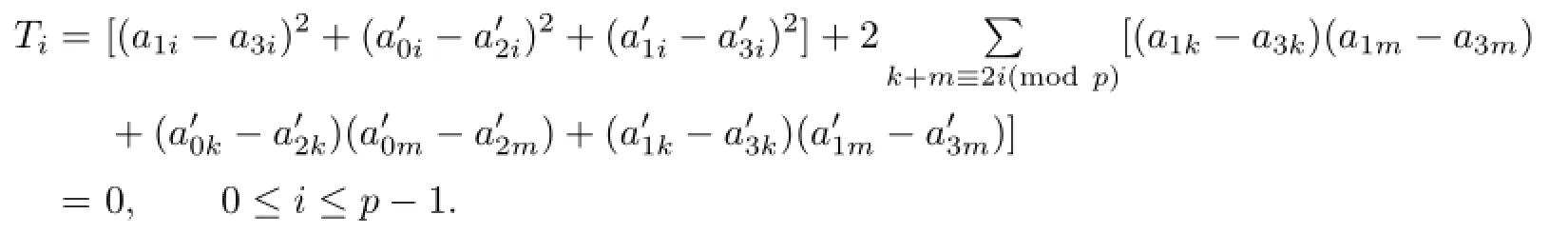
This shows that R5p(β)=0.Then we obtain that Ri(β)is nilpotent for 1≤i≤8,4p+1, 5p,and hence β is nilpotent inQ(K8×Cp).Thus,it is proved that the decomposition
U=α+β inQ(K8×Cp)is the desired.
Remark 2.1Recall that Ti=0 for 0≤i≤p−1.Then we have that

and(a1i−a3i),()and()either all are even,or two are odd and the other one is even.
Lemma 2.2([8],Lemma 8.3.5) Let A be a fnite abelian group.Then
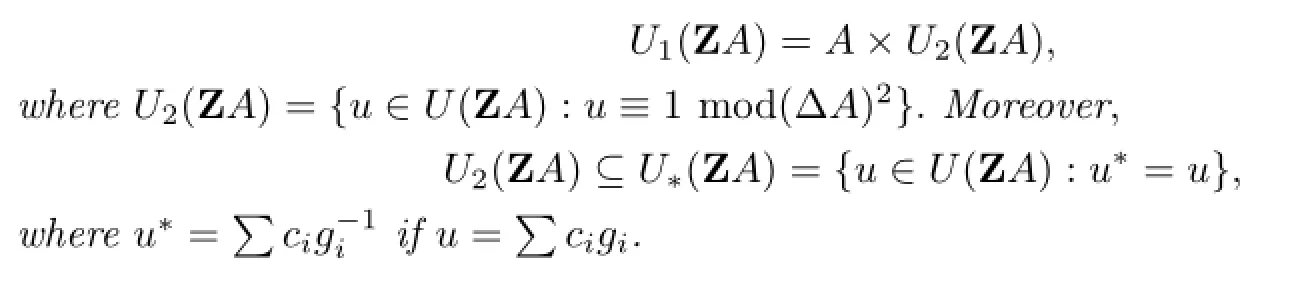
Lemma 2.3([9],Lemma 8.1) Let p be prime and m ≥1,ζpma primitive pmth root of unity.
(a)The cyclotomic units ofQ(ζpm)+are generated by−1 and the units

(b)The cyclotomic units ofQ(ζpm)are generated by ζpmand the cyclotomic units ofQ(ζpm)+.
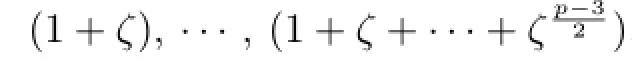
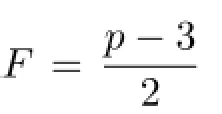
Let U={u|u=u0+u1ζ+u2ζ2+···+up−1ζp−1∈U(Z[ζ]),u0≡ 1(mod 2), ui≡0(mod 2)(1≤i≤p−1)}and U1={u|u∈U,∑ui=1}.
Proposition 2.1Let u=a0+a1ζ+a2ζ2+···+ap−1ζp−1∈U1and u2=b0+b1ζ+ b2ζ2+···+bp−1ζp−1.Then b0≡ 1(mod 4),b0≡ 1(mod 8),bi≡ 0(mod 4)and bi≡+2a0ai(mod 8)if i is even or bi≡+2a0ai(mod 8)if i is odd for 1≤i≤p−1. Moreover,if bi≡0(mod 8)for all 1≤i≤p−1,then≡1(mod 8)and if there is a bi≡4(mod 8)for some i,then u4≡1(mod 8).
Proof. Since Lemma 2.2 and u∈U1,ai=ap−i≡0(mod 2)for 1≤i≤p−1.Then
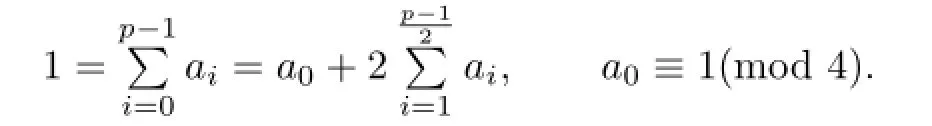
It is easy to calculate that
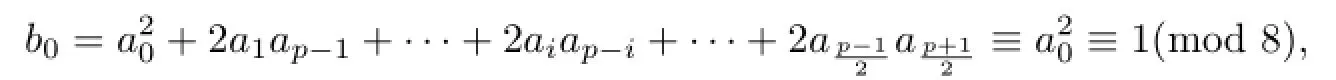
and for 1≤i≤p−1,
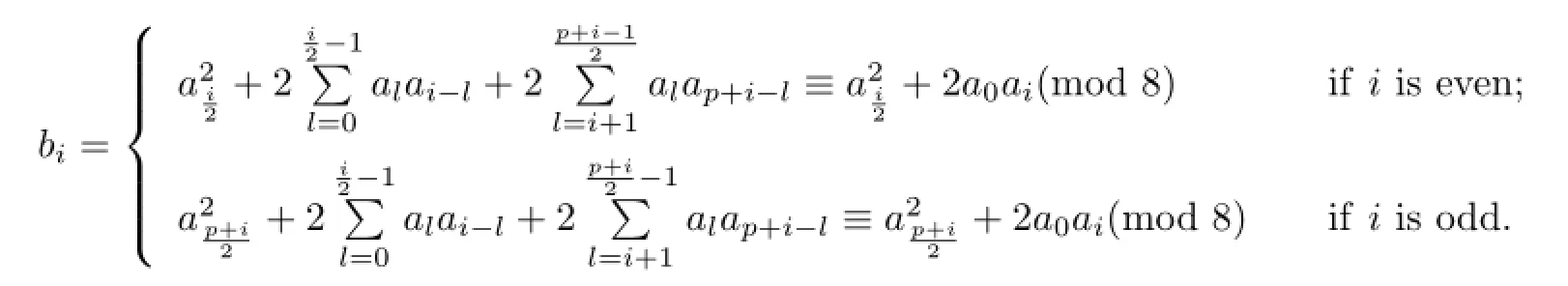
Similarly,the rest of the assertions is obvious.
Lemma 2.5Let b,c,d be even and a=0.If α,β,γ,δ are all inZ,then(a,b,c,d)(mod 8) just be(0,0,0,0),(0,0,4,4),(0,4,0,4),(0,4,4,0),(0,0,2,6),(0,2,0,6), (0,2,6,0),(0,0,6,2),(0,6,0,2),(0,6,2,0),(0,2,2,4),(0,2,4,2),(0,4,2,2), (0,6,6,4),(0,6,4,6)or(0,4,6,6)such that β,γ,δ either all are even,or one is even and the other two are odd.
Lemma 2.6Let b,c,d be odd and a=1.If α,β,γ,δ are all inZ,then(a,b,c,d)(mod 8) just be(1,1,1,1),(1,1,5,5),(1,5,1,5),(1,5,5,1),(1,1,3,7),(1,3,1,7), (1,3,7,1),(1,1,7,3),(1,7,1,3),(1,7,3,1),(1,3,3,5),(1,3,5,3),(1,5,3,3), (1,7,7,5),(1,7,5,7)or(1,5,7,7)such that β,γ,δ either all are even,or one is even and the other two are odd.

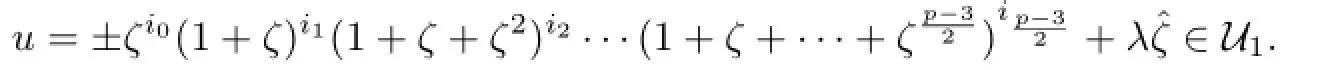
If there is no the item like(1+ζ+···+ζl)il(l is odd),then the sum of the coefcients of u−λˆζ is odd,thus λ is even,and there exists an integer j such that

If there is the item like(1+ζ+···+ζl)il(l is odd),then the sum of the coefcients of u−λˆζ is even,thus λ is odd,and there exists an integer k such that

Let p=5.We obtain the main results of the article in Section 3.
3 Z(K8×C5)Has the MJD Property
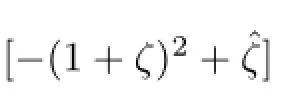
Proof.By Lemma 2.4,U1(Z[ζ])is generated by 1+ζ and ζ,then the 1-units ofZ[ζ]have the form±ζk(1+ζ)n+for some integer k,n and λ.Obviously,u=−(1+ζ)2+is a 1-unit ofZ[ζ],and n=2,λ=1 are the smallest positive integers such that
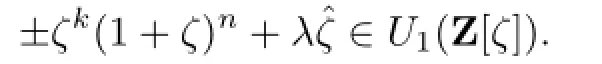
Therefore,the 1-units are generated by[−(1+ζ)2+and ζ.
Proposition 3.2Let u be the generator of U1.Then u≡1+6ζ+6ζ2+6ζ3+6ζ4(mod 8).
Proof. We observe that
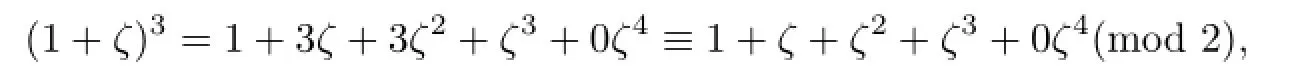
and n=3 is the smallest positive integer such that

for some positive integer k.By Proposition 3.1 and the defnition of U1,n=6 is the smallest positive integer such that±ζk(1+ζ)n+∈U1for some integer k and λ.Then the unique generator of U1should be
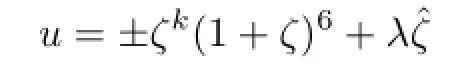
for k=2 and λ=5,i.e.,
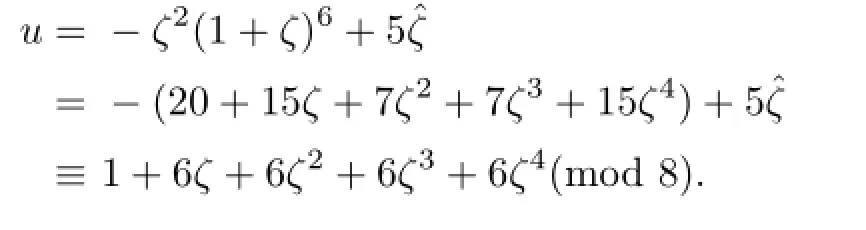
Theorem 3.1Integral group ringZ(K8×C5)has the MJD property.
Proof.For any U∈U1(Z(K8×C5)),by Theorem 2.1,U=α+β with α semisimple and β nilpotent inQ(K8×C5).Then it remains to show that β∈Z(K8×C5).Following Theorem 2.1,we have that
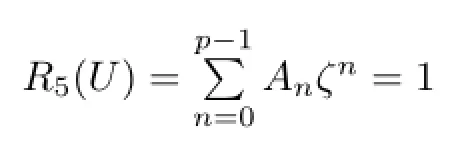
with A0=1 and An=0 for 1≤n≤p−1,
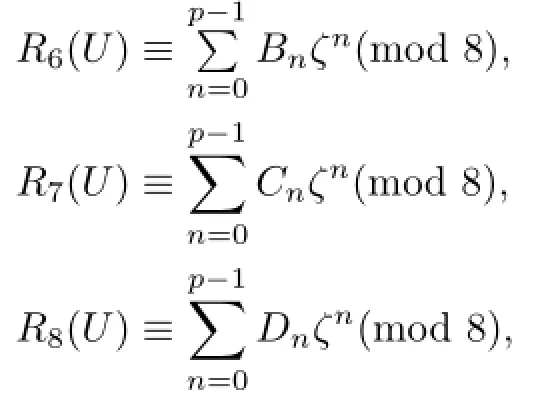
where 0≤Bn,Cn,Dn≤7.
Let
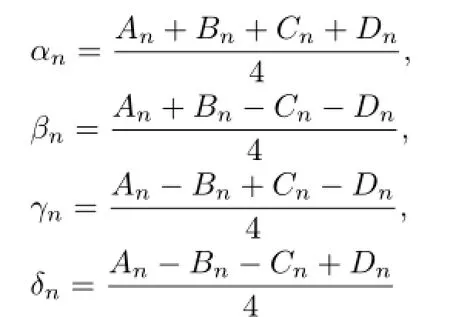
for 0≤n≤p−1.It is not difcult to see that
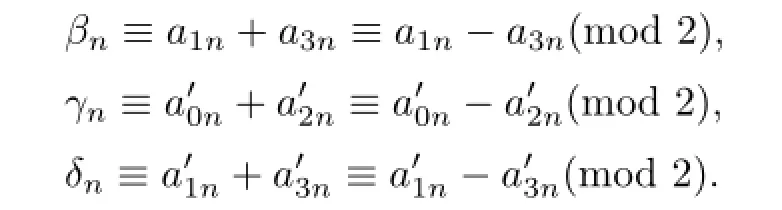
Recall Theorem 2.1 again,
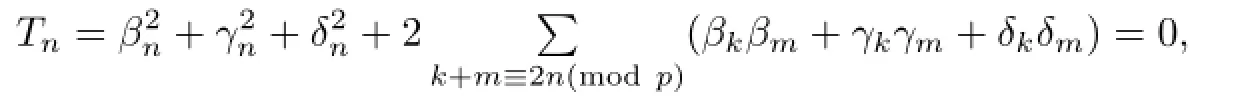
and hence,
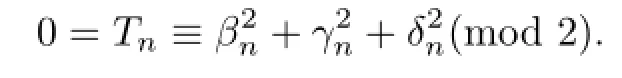
Thus,βn,γn,δneither all are even or one is even and the other two are odd.
Theorem 2.1 provides that all the coefcients of ζ,ζ2,···,ζp−1in R6(U),R7(U)and R8(U)are even,thus,R6(U),R7(U)and R8(U)are all in±U1.By Propositions 2.1 and 3.2,the generator u≡1+6ζ+6ζ2+6ζ3+6ζ4(mod 8)of U1is an element of order 2.Thus,
R6(U)(mod 8),R7(U)(mod 8),R8(U)(mod 8)∈{u,−u,1,−1}(mod 8).
By using Lemma 2.6,B0,C0,D0must all be 1(mod 8)since A0=1.Then
R6(U)(mod 8),R7(U)(mod 8),R8(U)(mod 8)∈{u,1}(mod 8),
and β0,γ0and δ0are all even.Since An=0,by Lemma 2.5,we obtain that
R6(U)≡1(mod 8), R7(U)≡1(mod 8), R8(U)≡1(mod 8),
and βn,γnand δnall are even for all 1≤n≤p−1,which deduces that β∈Z(K8×C5).
[1]Hales A W,Luthar I S,Passi I B S.Partial augmentations and Jordan decomposition in group rings.Comm.Algebra,1990,18:2327–2341.
[2]Hales A W,Passi I B S.Integral group rings with Jordan decomposition.Arch.Math.,1991,57:21–27.
[3]Hales A W,Passi I B S,Wilson L E.The multiplicative Jordan decomposition in group rings II.J.Algebra,2007,316:109–132.
[4]Arora S R,Hales A W,Passi I B S.Jordan decomposition and hypercentral units in integral group rings.Comm.Algebra,1993,21:25–35.
[5]Parmenter M M.Multiplicative Jordan decomposition in integral group rings of groups of order 16.Comm.Algebra,2002,30:4789–4797.
[6]Liu C H,Passman D S.Multiplicative Jordan decomposition in group rings of 3-groups.J.Pure Appl.Algebra,2009,8:505–519.
[7]Liu C H,Passman D S.Multiplicative Jordan decomposition in group rings of 2,3-groups.J. Pure Appl.Algebra,2010,9:483–492.
[8]Milies C P,Sehgal S K.An Introduction to Group Rings.Dordrecht:Kluwer,2002:237–258.
[9]Washington L C.Introduction to Cyclotomic Fields.Second Edition.Berlin:Springer-Verlag, 1996:278–286.
A
1674-5647(2017)01-0064-09
10.13447/j.1674-5647.2017.01.07
Received date:April 25,2016.
E-mail address:lanxiu0614@163.com(Wang X L).
2010 MR subject classifcation:16U60,20C05
 Communications in Mathematical Research2017年1期
Communications in Mathematical Research2017年1期
- Communications in Mathematical Research的其它文章
- L2-harmonic 1-forms on Complete Manifolds
- Trees with Given Diameter Minimizing the Augmented Zagreb Index and Maximizing the ABC Index
- Bonnesen-style Isoperimetric Inequalities of an n-simplex
- 2N+1-soliton Solutions of Boussinesq-Burgers Equation
- The Value Distribution and Normality Criteria of a Class of Meromorphic Functions
- Endpoint Estimates for Commutators of Fractional Integrals Associated to Operators with Heat Kernel Bounds
