基于决策粗糙集模型的局部属性约简

朱辉，窦慧莉

（江苏科技大学计算机科学与工程学院，江苏镇江212003）

近年来，随着互联网技术的迅猛发展，我们世界的信息量正在以爆炸性的速度增长着。各行各业均存在着大量的的信息，如何从中选取出有效的信息早已经成为我们亟待解决的一个难题。当前特征选择[2]已经成为了我们解决这一问题的最主要和高效的方法之一，也是学者们研究的重点之一[10]。

特征选择在Palwlak粗糙集模型[6]和其衍生模型中也被称为属性约简，是整个粗糙集领域中非常重要的一个方面。属性约简工作[8]的完善与否直接影响了我们整个模型在分类等方面的精度等指标的优劣。决策粗糙集模型(Decision-Theoretic Rough Set Model，DTRSM)是姚一豫教授在1989年提出基于Palwlak粗糙集模型的一个拓展模型的粗糙集模型。DTRSM解决了传统的粗糙集理论不涉及代价的问题，使得粗糙集也变得代价敏感，更加吻合实际生活中的语义。DTRSM提出之后，姚一豫教授在对其不断研究地过程中，提出了三支决策理论，其主要目的是为粗糙集正域、边界域和负域3个域提供合理的语义解释。之后很多学者基于这一模型进行了很多相关的研究。刘盾等对三支决策模型进行了深入的研究和拓展[14]。贾修一等基于三支决策进行了最小风险代价的研究[12]。然后，众多学者在研究过程中采用的都还是基于全部决策类的属性约简，在面对某个特定决策类进行属性约简的问题时，便造成了很大程度上的资源浪费和求解结果的不准确性。为此，程德刚教授[1]提出了局部的思想，只针对某个或多个需要考虑的决策类进行约束来求取约简。

1 相关概念

1.1 Pawlak粗糙集

粗糙集理论[1]是由波兰学者Pawlak提出的一种解决含糊性和不确定性问题的数学工具。其最主要是以集合近似的思想来进行相关的数据挖掘、数据分析和推理。粗糙集理论采用了基于等价关系的数据分析方法。

为了去刻画一个信息系统，Pawlak引入了上下近似集的概念。能根据条件判断出属于等价类X的元素构成的集合，我们称为X的下近似集；能根据条件判断出有可能属于等价类X的元素构成的集合，我们称为X的上近似集。

1.2 决策粗糙集理论（DTRS）与三支决策规则（Three-Way decision）

1.2.1 正域、负域、边界域

在上下近似集的概念之上，研究者将由其产生的划分区域分为3类：正域、负域以及边界域。正域即为下近似集合形成的划分区域；负域即为不属于上近似的区域；边界域变为上近似比下近似多出的一部分不确定性区域。

所以，正域和负域均为确定性的区域，而边界区域也是我们在判断问题的时候最关键的要素。如何减小不确定性也是本文我们讨论的一个关键点。

1.2.2 三支决策

三支决策是在传统的两支决策(接受、拒绝)上加入了延迟决策。定义分类状态Ω={X，～X}，动作集：t={eP，eB，eN}，其中：X表示成功划分进该域，～X则表示错误划分进该域。eP，eB，eN分别表示将一个对象划分进正域、边界域和负域的动作，那么划分的代价我们分别定义为：λPP，λPN，λBP，λBN，λNP，λNN。其中λPP、λBP、λNP分别表示正确将对象划分进正域、边界域、负域的代价；λPN，λBN，λNN则分别表示错误将对象划分进对应区域的代价。那么我们有如下代价表达式：

R(ep|[x]A)、R(eb|[x]A)、R(en|[x]A)表示划分在正域、边界域、负域的代价，由此可得总的划分代价：

2 属性约简

属性约简在粗糙及理论方面是极为重要的一个研究方向，它集中了该领域非常多的学者的关注。传统的粗糙集中属性约简效率一般，在处理许多复杂的数据时会消耗大量的时间，这无疑会大大降其应用的效率。针对这一问题，Yao等人将DTRS模型引入其中，并定义了包括保持正域和负域不变的属性约简在内的一系列属性约简方法。从该点出发，在本节我们将会把局部思想引入其中，分析DTRS模型在全局和局部条件下属性约简。

2.1 决策保持属性约简

粗糙集理论中，对于决策保持方法约简，通常是通过保持正域不变[12]或正域和负域二者不变来进行约简，以此保留完整的正域决策规则。本段我们将从保持正域和负域二者保持不变方面进行属性约简的研究。

定义 1在一个信息系统I=＜U，AT∪{d}＞，U为其论域，AT为其属性集，d为决策属性，∀A⊆AT，U/IND(d)={X1，X2，…，Xn}，∀Xj(j=1，2…n)，如果满足

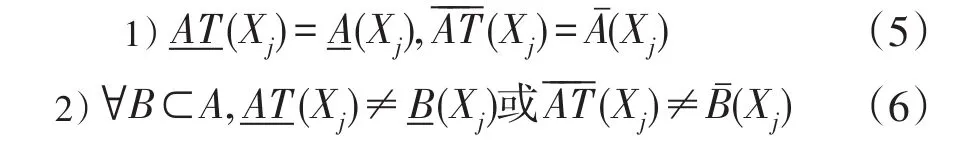
那么，我们称A是一个基于决策保持的全局属性约简。

定义表明：一个约简如果满足保持上下近似集不变即正域和负域不变，便能保持了决策规则的完整。我们就可以将其称为决策保持属性约简。

定义2在一个信息系统I=＜U，AT∪{d}＞，U为其论域，AT为其属性集，d为决策属性，∀A⊆AT，U/IND(d)={X1，X2，…，Xn}，如果对于一个或多个指定Xj(j=1，2…n)，如果满足：

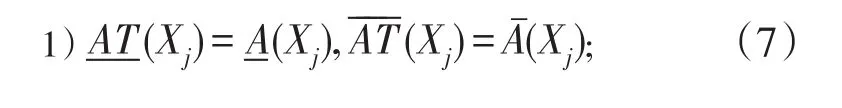
那么，我们称A是一个基于决策保持的局部属性约简。

定义2是我们引入局部思想后的一个变形的公式。正如实际应用中可能遇到的，只需针对少数关键性对象进行有针对行属性筛选一样，我们只是在需要考虑的决策类中做决策保持的工作，对于不需要考虑的决策类中我们无需浪费效率对其进行决策保持。由此可以得到与我们考虑决策类最相关的属性。

2.2 决策单调属性约简

定义 3在一个信息系统I=＜U，AT∪{d}＞，U为其论域，AT为其属性集，d为决策属性，∀A⊆AT，U/IND(d)={X1，X2，…，Xn}，∀Xj(j=1，2，…，n)，如果满足

那么，我们称A是一个基于决策单调的全局属性约简。

定义 4 在一个信息系统I=＜U，AT∪{d}＞，U为其论域，AT为其属性集，d为决策属性，∀A⊆AT，U/IND(d)={X1，X2，…，Xn}，如果对于一个或多个指定Xj(j=1，2…n)，如果满足

那么，我们称A是一个基于决策单调的局部属性约简。

定义4相比与定义3而言，着重关注了需要关键性对象的属性，弱化了非关键性对象在其中的影响。这将会有助于我们筛选出最能够刻画关键性对象的对应属性。

3 测试基于三支决策规则的属性约简

3.1 实验算法

3.1.1 重要度函数

文中采用了启发式算法(Heuristic)，高效地获取属性约简。在启发式算法中，最为重要的便是重要度的定义和计算。在文中，重要度函数按如下的定义给出：

定义5令AT为属性集合，A⊂AB，a∈AT，U/IND(d)={X1，X2，…，Xn}，决策保持重要度函数：

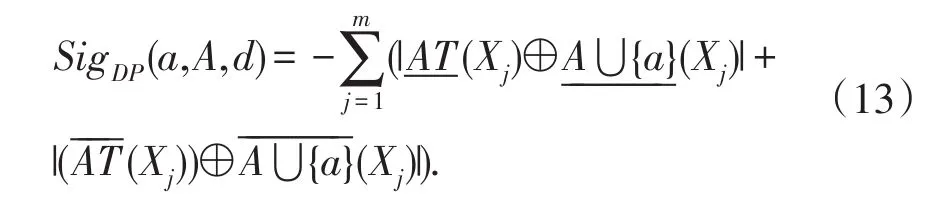
其中，∀X，Y⊆U，X⊕Y=(X-Y)+(Y-X)

定义6令AT为属性集合，A⊂AT，a∈AT，U/IND(d)={X1，X2，…，Xn}，决策保持的重要度函数：

其中，如果X⊆Y，X⊙Y=|Y-X|；否则，X⊙Y=-∞。

3.1.2 算法流程

属性约简的启发式算法

该算法中，第二步每次计算后校验得到的约简是否满足指定约简条件(定义1～4)，满足条件添加元素进Red集合，否则不添加；第三步，在添加的元素中再次检查是否存在冗余属性，有则删除。

4 实验分析

为了验证第1节中Local思想的性能上的优越性，本小节中通过约简后属性的个数和规则数目两个方面为标准，对本文中的理论进行实验。实验硬件配置Inter Core i3 CPU（2.67 GHz）、内存4.0 GB的计算机上，用Matlab R2010b实现算法，其中实验中所用的数据集信息如表1，实验数据集均来自于UCI标准数据集。

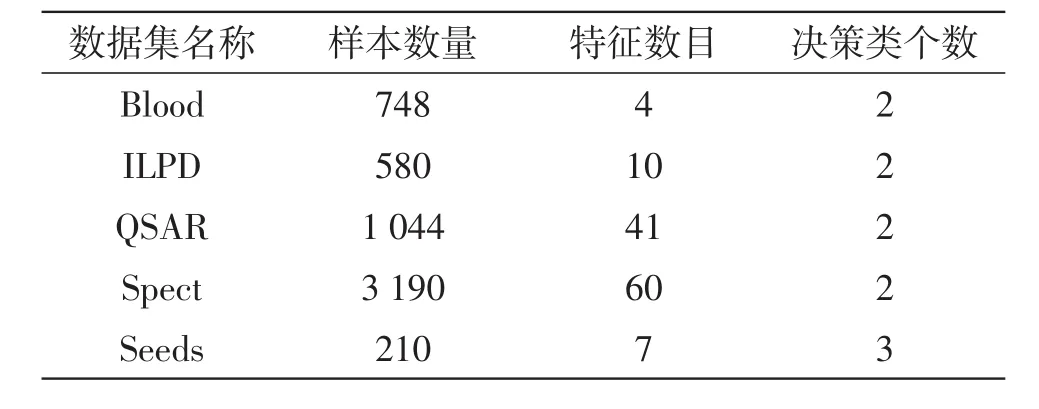
表1 实验数据集及其相关信息

表2 全局约简和局部约简下的属性数目（10组数据平均值）

表2所示为基于决策保持的全局属性约简和局部属性约简实验的对比结果。以Blood数据集为例，在达到相同的目的（决策保持）的前提下，局部约简可以得到更为精确的属性，在相同的方法下，平均多约简了12.5%的冗余属性。因此，局部属性约简在约简后的属性（特征）数目方面比全局属性约简要有优势。基于这一优点我们可以在属性约简的试验中加入局部的思想可以提高效率，节省资源，避免浪费。

表3 全局约简和局部约简下的确定性规则变化（10组数据平均值）

表3显示的是全局约简和局部约简在规则数方面的结果，从该表中我们可以看出：局部下的实验结果的规则数相比于全局下有了不同程度的增长。以Blood数据集为例，由于它是一个二类的数据集，所以只有X1和X2两个等价类。基于X1这个等价类，规则数量不变，但是基于X2下规则数量有了明显的增加，从平均90.4条规则增加到了97.9条规则数，有了8.3%的提升。这对于我们在辅助决策等方面具有较为重要的意义。

5 结束语

本文基于三支决策规则，对局部思想进行了属性约简方面的研究。通过对比局部约简和全局约简的定义认识局部约简的原理与可能优点。再结合算法、实验，用实验结果来验证理论。由结果可知：局部属性约简在删除冗余属性和确定性规则获取等方面较全局属性约简相比具有明显优势。这将会对我们研究决策问题提供较为重要的作用。在本文研究的基础上，下一步研究主要集中在：

1）通过局部思想和其他算法结合挖掘其在属性约简方面的优点；

2）将局部思想应用和其他约简方法结合，进一步挖掘和认识局部思想。

[1]Chen DG，Zhao SY.Local reduction of decision system with fuzzy rough sets[J].Fuzzy Sets and Systems，2010（161）：1871-1883.

[2]Chen G，Chen J.A novel wrapper method for feature selection and its applications[J].Neurocomputing，2015（159）：219-226.

[3]Lee J，Kim DW.Fast multi-label feature selection based on information-theoretic feature ranking[J].Pattern Recognition，2014（48）：2761-2771.

[4]Jia X Y，Liao W H，Tang Z M，et al.Minimum cost attribute reduction in decision-theoretic rough set models[J].Information Sciences，2013（219）：151-167.

[5]Jiang F，Sui Y F，Zhou L.A relative decision entropy-based feature selection approach[J].Pattern Recognition，2015（48）：2151-2163.

[6]Pawlak Z.Rough Sets-theoretical aspects of reasoning about data[J]. Dordrecht：Kluwer Academic，1991.

[7]Qian Y H，Liang J Y，Pedrycz W，et al.Positive approximation：An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence，2010（174）：597-618.

[8]Shu W H，Qian W B.A fast approach to attribute reduction from perspective of attribute measures in incomplete decision systems[J].Knowledge-Based Systems，2014（72）：60-71.

[9]Wang W Y，Ma X A，Yu H.Monotonic uncertainty measures for attribute reduction in probabilistic rough set model[J].International Journal of Approximate Reasoning，2015（59）：41-67.

[10]Zeng Z L，Zhang H J，Zhang R，et al.A novel feature selection method considering feature interaction[J].Patten Recognition，2015（48）：2656-2666.

[11]Zong W，Wu F，Chu L K，et al.A discriminative and semantic feature selection method for text categorization[J].Int.J.Production Economics，2015（165）：215-222.

[12]贾修一，商琳，李家俊.决策风险最小化属性约简[J].计算机科学与探索，2011，5（2）：155-160.

[13]贾修一，商琳.一种求三支决策阈值的模拟退火算法[J].小型微型计算机系统，2013，11（34）：2603-2606.

[14]刘盾，姚一豫，李天瑞.三枝决策粗糙集[J].计算机科学，2011，1（38）：246-250.

[15]宋晶晶，杨习贝，戚愑，等.可调节模糊粗糙集：模型与属性约简[J].计算机科学，2014，12（41）：183-188.