斜交轴线齿轮线齿精确几何模型的构建方法*
陈扬枝 陈汉飞
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
线齿轮(LG)[1]的啮合原理不同于经典齿轮[2],它只需保证齿轮副中的一对共轭空间曲线在任意时刻相切接触于一个点且在接触点处有公共的主法矢,就可以实现齿轮连续传动.2007年,这种基于空间曲线啮合原理而设计的齿轮被提出[3- 4],其后被命名为线齿轮[1].线齿轮啮合原理的数学表达(即啮合方程表达式)为[1]
v12·β1=0
(1)
式中,v12是共轭空间曲线啮合点处的相对速度,β1是主动接触线在啮合点处的主法矢.
线齿轮可分为斜交轴线齿轮和交错轴线齿轮[5].两齿轮轴在同一平面上的是斜交轴线齿轮,齿轮轴不在同一平面上的是交错轴线齿轮.文献[6]提到的正交轴线齿轮可以看作是斜交轴线齿轮的一个特例.文中主要研究斜交轴线齿轮.
前期对斜交轴线齿轮的几何学研究主要集中在主、从动线齿接触线方程[7- 8],线齿受力结构的优化设计[9- 11],线齿滑动率[12],线齿重合度[13]等方面,并通过进一步研究制定了斜交轴线齿轮的强度设计准则以及几何参数设计、选择准则.在斜交轴线齿轮的应用研究方面,学者们发明并探讨了多面体线齿轮变速器[14- 16]以及带有线齿轮增速器的一种新型风力发电机[17]等.
文献[7]中提出了一种斜交轴线齿轮不等直径线齿构建方法,建立了线齿中心线方程.尽管按文献[7]的线齿设计方法无法在三维CAD软件上建立线齿的精确几何模型,但理论上所设计的线齿轮只要主、从动接触线满足式(1),就能保证线齿轮正确啮合传动[1].实际上,相关运动学实验结果[7,18]也表明,只需保证主、从动接触线精度,无论是否构建精确的线齿三维几何模型,都可以保证斜交轴线齿轮完成稳定的啮合传动.但是,在斜交轴线齿轮弹流润滑设计理论的研究中,需要对线齿轮啮合点处形成的椭圆接触进行精确的几何分析,因此,首先必须建立精确的线齿三维几何模型,同时,在通用的三维CAD软件上建立精确的线齿齿面几何模型,这将大幅提高线齿轮设计和相关参数计算的效率.但迄今为止, 在此领域的线齿轮几何学研究仍处于空白.有鉴于此,文中研究斜交轴线齿轮的线齿精确几何模型构建方法,主要是修正斜交轴从动轮的中心线方程,推导斜交轴线齿轮的线齿曲面方程,研究在三维CAD软件上建立与线齿曲面方程理论描述结果一致的线齿实体几何模型的通用方法,并通过运动学仿真探讨修正后的线齿模型对啮合传动的影响.
1 斜交轴线齿轮线齿曲面模型的建立
1.1 线齿曲面模型坐标系的建立

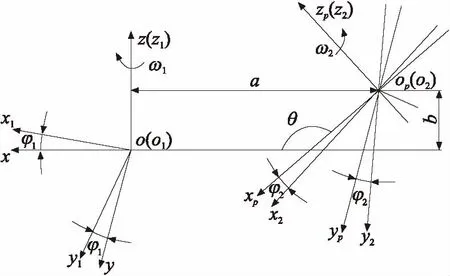
图1 斜交轴线齿轮坐标系[7]Fig.1 Coordinates of the arbitrary intersecting line gear[7]
为使曲面方程表达更简洁,需要在图1基础上再建立一个新的固定坐标系oq-xqyqzq.该坐标系是由o-xyz坐标系向x轴负方向移动距离m1所得.固定坐标系如图2所示.

图2 线齿轮固定坐标系Fig.2 Fixed coordinates of the line gear
斜交轴线齿轮曲面方程建立的相关讨论主要集中在oq-xqyqzq坐标系上,把oq-xqyqzq坐标系从上述固定坐标体系中提取出来,如图3所示.
推导斜交轴线齿轮线齿曲面方程需要用到的坐标系转换矩阵如下:

为oq-xqyqzq坐标系中主动接触线啮合点的单位副法矢;M、M1、M2分别为齿轮副啮合点、主动线齿截面的中心点以及从动线齿截面的中心点
图3oq-xqyqzq坐标系
Fig.3oq-xqyqzqcoordinates
o-xyz和oq-xqyqzq的转换矩阵为
(2)
o1-x1y1z1和o-xyz的转换矩阵为
(3)
o-xyz和op-xpypzp的转换矩阵为
(4)
op-xpypzp和o2-x2y2z2的转换矩阵为
(5)
式中,i12为线齿轮传动比,t为接触线参变量,m1为主动接触线的螺旋半径.
1.2 主动线齿曲面模型的建立
主动轮一般选用圆柱螺旋线作为接触线.在o1-x1y1z1转动坐标系中,主动接触线R的方程为


(6)

在oq-xqyqzq坐标系中,由转换矩阵(2)、(3)和式(6)可得R的表达式如下:


(7)
在文献[7]中,线齿轮线齿截面的中心点由啮合点沿着主动接触线在该点处的副法矢γ1方向平移得到,主动线齿截面的中心点由啮合点沿着γ1负方向移动距离r1得到,从动线齿截面的中心点由啮合点沿着γ1正方向移动距离r2得到.据此设计方法建立主动线齿曲面方程.
在o1-x1y1z1坐标系中,主动接触线啮合点的单位副法矢γ1表达式为
(8)
在o-xyz坐标系中,由转换矩阵(3)和式(8)可得γ1表达式如下:
(9)
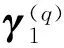
在oq-xqyqzq坐标系中,根据文献[7]的方法建立中心线方程Rz,由式(7)和(9)可得Rz方程如下:

(10)
根据式(10),在oq-xqyqzq坐标系中建立主动线齿曲面截面,见图4.为保证线齿结构合理,截面应平行于xq轴,截面边界上的点即为线齿曲面上的点.

图4 主动线齿截圆Fig.4 Circular cross-section of the driving line teeth
选取圆作为主动线齿截面形状,截面简称截圆.截圆角度参数为δ1,δ1逆时针增大,初始位置指向zq轴.
在oq-xqyqzq坐标系中,由式(10)可得主动线齿截圆Σ1(δ1)方程如下:


(11)

在o1-x1y1z1坐标系中,由转换矩阵(2)、(3)和式(11)可得主动线齿曲面Σ1的方程如下:
(12)
根据式(12),选用如表1所示的线齿参数,并使用数学软件Mathematica 10.0进行单根主动线齿几何建模,结果如图5所示.
为了应用三维CAD软件建立精确的线齿几何模型,需要对主动线齿的构建方法进行进一步分析.

图5 主动线齿曲面几何模型Fig.5 Surface geometric model of the driving line teeth
在oq-xqyqzq坐标系中,主动接触线啮合点处的切矢α1表达式为
(13)
三维CAD软件无法像数学软件那样通过几何方程直接生成线齿三维曲面或者实体.在三维CAD软件中建立如图5所示的主动线齿的曲线轴柱体,首先要建立截面和轨迹线,必要时还需要建立辅助轨迹线(如中心线),然后通过扫描形成曲线轴柱体.文中以三维CAD软件Pro/E为例说明构建线齿精确几何模型的方法.
利用Pro/E软件中的“扫描混合”工具,定义所有 “截平面” (截圆) “垂直于轨迹”(接触线).同时在草绘截圆时,保证圆心在“x轨迹” (中心线)上,最后完成扫描.如此可建立理论上与式(12)所描述的几何模型一致的主动线齿三维模型,如图6所示.
图6中,主动线齿轮的其余各齿都可依此方法或通过“阵列”工具建立.其他三维CAD软件也可以用类似方法建立主动线齿曲面的精确模型.简而言之,应用三维CAD软件构建精确的线齿曲面几何模型,要求在建立线齿曲面方程时,截圆垂直于接触线切矢.
根据上文的分析,按照文献[7]设计方法建立的主动线齿曲面方程符合这一要求,所以能够通过三维CAD软件建立精确的主动线齿曲面几何模型.

图6 主动线齿模型Fig.6 Models of the driving line teeth
1.3 从动线齿曲面模型的建立
为了能在三维CAD软件上进行从动线齿曲面的精确几何建模,同理,要求从动线齿曲面中任一截面都垂直于从动接触线切矢α2.
在oq-xqyqzq坐标系中,α2表达式为
(14)
式中:m2是从动接触线螺旋半径,其表达式为

(15)
a、b是从动轮位置参数,其具体含义如图1所示.


(16)
如图7所示,将啮合点M沿k正方向移动距离r2,得到新的中心点M2.由式(7)和(16)可得新的从动线齿中心线Rcz方程如下:

(17)

图7 线齿截圆Fig.7 Circular cross-section of the line teeth
根据式(17)建立从动线齿截圆.如图7所示,截圆角度参数为δ2,δ2逆时针增大,初始位置的指向与矢量k相同.
在oq-xqyqzq坐标系中,由式(17)可得从动线齿截圆Σ2(δ2)方程为
(18)
式中,ε2是矢量k与yq轴的夹角,则有
ε2=arctan (m2/(i12n)).
在o2-x2y2z2坐标系中, 由转换矩阵(2)、(4)、(5)和式(18)可得从动线齿曲面Σ2方程如下:
(19)
式中,A、B、C表示为

C=α-m1+r2sinδ2.
根据式(19),选用表1所示线齿参数, 并使用数学软件对单根从动线齿进行几何建模,结果见图8.

图8 从动线齿曲面几何模型Fig.8 Surface geometric model of the driven line teeth
按照与主动线齿相同的构建方法,应用Pro/E软件建立从动线齿轮的单根线齿模型,如图9所示.其他从动线齿可依相同方法构建完成.

图9 从动线齿模型Fig.9 Models of the driven line teeth
2 仿真实验
为了建立精确的线齿实体几何模型,上文修正了从动线齿中心线方程,并通过新的从动线齿中心线方程(式(17))和接触线方程(式(7))构建了从动线齿曲面几何模型.本节将应用Pro/E软件对线齿轮副进行完整的实体几何建模,并进行运动学仿真,以验证修正后的线齿轮副是否能够正确啮合传动.
所选用的线齿轮参数见表1.表1中,各齿轮参数根据文献[12- 13]中的参数选择准则选取.

表1 线齿轮参数1)Table 1 Parameters of the line gear
1)表中,m1、n、r1、r2、a、b的单位均为mm,θ的单位为(°).
根据式(12)、(19)以及图1所示的斜交轴线齿轮坐标系,建立主、从动线齿轮几何模型.实际应用的线齿轮的轮体模型如图5和8所示,其线齿附着在轮体上[18],这样设计的线齿刚度很好.但这种轮体实体模型不利于观测轮体的运动学仿真过程.因此,这里的运动学仿真采用钩杆状的线齿设计,如图10所示.

图10 主、从动线齿轮模型Fig.10 Models of the driving and driven line teeth
通过Pro/E把图10设计的交叉轴主、从动线齿轮“装配”起来,结果如图11所示,其中的线齿轮轮体结构部分已被“隐藏”.然后,利用Pro/E中的“机构”模块对线齿轮副进行运动学仿真.该仿真过程是观察其中一对线齿从开始啮合到脱离啮合的传动过程,每1/6行程记录一次啮合情况.图11(a)-11(e)分别是按照开始啮合到脱离啮合的时间顺序记录下来的啮合情况.
图11的仿真结果表明,从动线齿中心线的修正对啮合没有影响,修正后的线齿轮副能够实现正确的啮合传动.所以,式(12)和(19)可以分别应用于斜交轴线齿轮副主、从动线齿的精确齿面模型构建,文中研究的线齿曲面的精确几何模型构建方法可以应用于斜交轴线齿轮副椭圆接触的几何模型分析,为斜交轴线齿轮的弹流润滑设计理论提供几何学基础.

图11 仿真结果Fig.11 Simulation results
3 结语
为了建立斜交轴线齿轮副线齿曲面的精确几何模型,为线齿轮副的弹流润滑理论提供齿面接触几何学基础,文中进行了以下工作:(1)建立了斜交轴主动线齿曲面方程,并研究了应用三维CAD软件实现主动线齿精确建模的方法,应用三维CAD软件所构建的线齿几何实体模型与推导所得的主动线齿曲面方程的理论描述结果是完全一致的.(2)根据三维CAD软件的特性,修正了从动线齿中心线方程,并利用新的从动线齿中心线方程和从动接触线方程建立了斜交轴从动线齿曲面方程;建立了应用三维CAD软件实现从动线齿精确建模的方法;应用三维CAD软件所建立的线齿几何实体模型与推导所得的从动线齿曲面方程描述的理论结果是完全一致的.(3)应用Pro/E软件建立了斜交轴线齿轮副线齿精确模型,运动学仿真实验表明,修正后的从动线齿并不影响线齿轮副的啮合传动.
文中提出的线齿曲面的精确几何模型构建方法为后续斜交轴线齿轮的点接触弹流润滑研究打下了良好的基础,同时斜交轴线齿轮线齿的精确建模也为交错轴线齿轮的精确建模提供了重要参考.在此基础上,下一阶段将进一步研究线齿齿廓形状对点接触弹流润滑的影响,并通过仿真分析结合传动效率试验测试的方法找到最佳齿形方案,最终完善线齿轮摩檫学设计.
[1] 陈扬枝.线齿轮 [M].北京:科学出版社,2014:3- 4.
[2] 吴序堂.齿轮啮合原理 [M].西安:西安交通大学出版社,2009:145- 147.
[3] CHEN Yang-zhi,XING Guang-quan,PENG Xue-fei.The space curve mesh equation and its kinematics experiment [C]∥Proceedings of the 12th IFToMM World Congress.Besancon:IFToMM,2007:18- 21.
[4] CHEN Yang-zhi,XIANG Xiao-yong,LUO Liang.A corrected equation of space curve meshing [J].Mechanism and Machine Theory,2009,44(7):1348- 1359.
[5] CHEN Yang-zhi,LV Yue-ling,DING Jiang,et al.Fundamental design equations for space curve meshing skew gear mechanism [J].Mechanism and Machine Theory,2013,70(6):175- 188.
[6] 何恩义,陈扬枝,陈祯.装配误差对正交轴空间螺旋线齿轮传动的影响 [J].华南理工大学学报(自然科学版),2012,40(12):24- 29.
HE En-yi,CHEN Yang-zhi,CHEN Zhen.Effects of assembly errors on transmission precision of space curve meshing wheel [J].Journal of South China University of Technology(Natural Science Edition),2012,40(8):55- 58.
[7] DING Jiang,CHEN Yang-zhi,LV Yue-ling.Design of space-curve meshing-wheels with unequal tine radii [J].Strojniški Vestnik-Journal of Mechanical Engineering,2012,58(11):633- 641.
[8] CHEN Zhen,CHEN Yang-zhi,DING Jiang.A generalized space curve meshing equation for arbitrary intersecting gear [J].Proceedings of Institution of Mechanical Engineers Part C:J Mechanical Engineering Science,2013,227(7):1599- 1607.
[9] CHEN Yang-zhi,HU Qiang,SUN Lei-hou.Design criterion for the space-curve me-shing-wheel transmission me-chanism based on the deformation of tines [J].Journal of Mechanical Design,2010,132(5):1- 6.
[10] CHEN Yang-zhi,LIANG Shun-ke,DING Jiang.The equal bending strength design of space curve meshing wheel [J].Journal of Mechanical Design,2014,136(6):061001/1- 10.
[11] CHEN Yang-zhi,LIANG Shun-ke.Research on the maximum bending stress on driving tine of SCMW [J].Applied Mechanics and Materials,2012,184/185(1/2/3):445- 449.
[12] DING Jiang,CHEN Yang-zhi,LV Yue-ling.Position-parameter selection criterion for helix-curve meshing-wheel mechanism based on sliding rates [J].Strojniški Vestnik-Journal of Mechanical Engineering,2014,60(9):561- 570.
[13] CHEN Yang-zhi,DING Jiang,LV Yue-ling.Geometric constraints and interference-proof conditions of helix-curve meshing-wheel mechanism [J].Transactions-Canadian Society for Mechanical Engineering,2015,39(1):13- 28.
[14] CHEN Yang-zhi,DING Jiang,YAO Chuang-hai,et al.Polyhedral space curve meshing reducer with multiple output shafts [C]∥Proceedings of the ASME 2012 International Mechanical Engineering Congress & Exposition(IMECE2012).Houston:ASME,2012:9- 15.
[15] 陈扬枝,丁江.多轴输出的多面体空间曲线啮合变速器:201010511625.6 [P].2012- 07- 18.
[16] CHEN Yang-zhi,CHEN Zhen,DING Jiang.Space curve mesh transmission pair and polyhedral space curve mesh transmission:PCT/CN2010/078294:US 8,789,438 B2 [P].2014- 07- 29.
[17] 崔秀燕.基于线齿轮传动的半直驱式小型风力发电机 [D].广州:华南理工大学,2016.
[18] CHEN Yang-zhi,HUANG Huai,LV Yue-ling.A variable-ratio line gear mechanism [J].Mechanism & Machine Theory,2016,98:151- 163.
[19] 李瑰贤.空间几何建模及工程应用 [M].北京:高等教育出版社,2007:11- 16.

