MATLAB在平面桁架计算中的应用
王鹏+周琪琛+姚姗姗
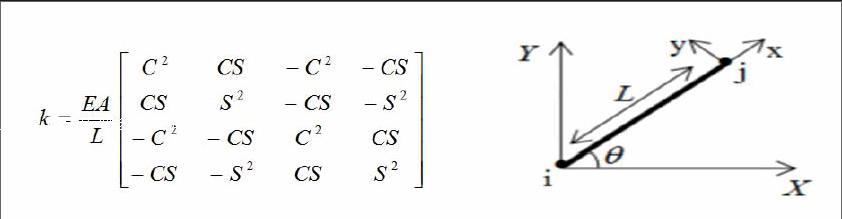
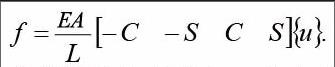
摘 要:本文基于平面桁架有限元分析的基本原理,利用MATLAB语言编程对有外荷载作用的平面桁架进行有限元分析,结果表明,通过MATLAB软件对平面桁架受力分析的结果与精确解吻合。本文介绍的方法,在平面桁架有限元中具有普遍的适用性,对复杂的平面桁架结构有限元分析有一定的参考价值。
关键词:平面桁架;MATLAB;有限元分析
MATLAB是以矩阵为基本的运算单元,可以灵活地进行矩阵运算、图形绘制、编程开发等,具有编程效率高、可移植性强、计算速度快等特点;有限元分析法是根据变分原理求解数学及物理问题的数值计算方法,它是随着近年来计算机技术的迅速发展而得到的广泛应用。本文以解决一个实际的平面桁架问题为例,运用有限元分析法,并利用MATLAB软件进行编程计算来演示MATLAB软件在平面桁架中的应用。接下来,首先介绍解决平面桁架问题的有限元分析方法。
1 平面桁架有限元分析的基本原理
在用有限元法对平面桁架受力分析中,平面桁架元是分析的基本单元,它是一种二维有限元,每个平面桁架元有2个节点和3个参数,参数分别为长度L、弹性模量E和横截面积A,当假设桁架元与正方向总体X轴逆时针倾斜θ角时,并令C=Cos(θ),S=Sin(θ),则单元刚度矩阵可表示为:
在有限元分析中,通过单元分析,建立单元刚度矩阵k,然后再将单元刚度矩阵通过刚度集成规则集合成结构的整体刚度矩阵K,对于一个有n个节点的结构而言,其整体的刚度矩阵K为2n×2n的矩阵,在实际MATLAB软件操作中,并不需要编写函数程序,而是直接调用相应的函数即可,正是因为这样,在用MATLAB软件进行桁架受力分析时,可以大大提高效率,节省时间。整体刚度矩阵的函数名称为PlaneTrussAssemble。一旦得到刚度矩阵K,就可以列出方程:
式中,U代表节点的位移矢量,F是结构节点的荷载矢量,这两个边界条件需要手动赋值,然后利用高斯消元法便可求解上述方程组,一旦求解出为止的位移和支反力,就可以利用方程:
求解单元的节点力。式中f代表单元节点力,u是单元节点的位移矢量,最后,将单元节点力除以桁架的横截面积便可以得到单元应力,之后就可以进行结构校核、结构安全性检验等一系列力学性实验分析。
2 有限元法分析的一般步骤
有限元法是一种高效能、普遍使用的数值计算方法,随着近年来计算机技术的迅速进步,有限元法得到了广泛的使用和发展,对于有限元法分析的步骤,不同书籍的介绍不尽相同,但大体上可以分为以下几步:
离散化域:将结构分解为独立的单元和节点,对于桁架和钢架这类的离散系统,这一步可以省略,对于其他的连续性结构,如板壳,这一步就显得尤为重要,离散化的好坏直接影响到最后结果的准确性。
得到单元刚度矩阵:由上一步离散化处理的结果,写出每个单元的刚度矩阵,这一步可以通过调用MATLAB工具箱来完成,相应函数的使用方法将在下面的实例中做出介绍。
集成整体刚度矩阵:根据上一步得到的单元刚度矩阵,通过刚度集成规则,集成结构整体的刚度矩阵,这一步也可以直接用MATLAB工具箱来完成,
引入边界条件:所谓的边界条件是指位移、外加荷载、支座类型等,不同结构的边界条件不尽相同,所以这一步需要手动赋值,具体的操作步骤会在案例中演示。
解方程:在这一步中,需要对整体刚度矩阵进行分解,然后再用高斯消去法求解方程组,在用高斯消去时,有时候需要手动分解矩阵。
后处理:当需要得到其他信息时,如支反力、单元节点力、单元应力等,还需要进行后处理工作,这一步需要操作者掌握一定的材料力学方面的知识。
3 实例分析
为了进一步说明MATLAB在平面桁架计算中的作用,接下来通过计算一个实例,来演示有限元法分析平面桁架问题的具体操作步骤。
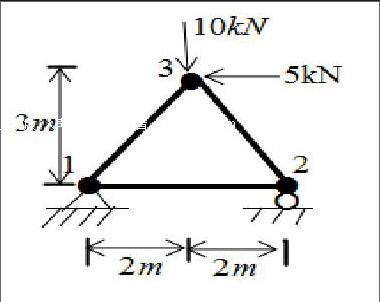
如图为一平面桁架结构,为了便于计算,
假定结构的弹性模E=200GPa
横截面积A=2cm2,结构受力如图所示:
先对结构进行离散化处理,由于桁架结构已经是离散化结构,所以我们只需要将结构单元编号即可:
接下来多次调用MATLAB的PlaneTrussElementStiffness函数,分别生成单元刚度矩阵k1、k2、k3。然后集成整体刚度矩阵,由于该结构有3个节点,所以整体刚度矩阵为6×6矩阵,在生成整体刚度矩阵前,要先建立一个6×6的零矩阵,零矩阵可以手动设置,也可以直接调用MATLAB的zeros()函数直接生成相应的零矩阵,得到零矩阵后,再反复调用planeTrussAssemble函数生成整体刚度矩阵K,由于本题结构只有3个单元,所以只需调用3次该函数即可;得到整体刚度矩阵后,就可以建立该结构的矩阵方程[K]{U}={F},再输入边界条件,本题的边界条件为U1x=U1y=U2y=0,F2x=0,F3x=5,F3y=-10 。接着手动分解方程并通过MATLAB软件用高斯消法求解方程,便可得到节点的位移,最后一步就是后处理,这一步需要看题目要求解什么未知数,如求外力,用F=K*U等式便可求解,然后调用PlaneTrussElementstress函数即可求出。下面是该实例在用MATLAB软件求解的程序:
% 输入参数 E=200e6;A=2e-4;
% 计算各杆的长度
L1=4;L2=PlaneTrussElementLength(0,0,2,3);L3=PlaneTrussElementLength(4,0,2,3);
% 计算单元刚度矩阵,
k1=PlaneTrussElementStiffness(E,A,L1,0);theta2=atan(3/2)*180/pi;theta3=180-theta2;k2=PlaneTrussElementStiffness(E,A,L2,theta2);k3=PlaneTrussElementStiffness(E,A,L3,theta3);
% 建立零矩阵 K=zeros(6,6);
% 整体的刚度矩阵
K=PlaneTrussAssemble(K,k1,1,2);K=PlaneTrussAssemble(K,k2,1,3);K=PlaneTrussAssemble(K,k3,2,3);
% 引入边界条件,手动赋值 k=[K(3,3),K(3,5:6);K(5:6,3),K(5:6,5:6)];
% 外力 f=[0;-5;-10];
% 利用高斯消去法解方程组 u=k\f; U=[0;0;u(1);0;u(2:3)];
% 计算节点力矢量 F=K*U;
% 调用节点位移矢量
u1=[U(1);U(2);U(3);U(4)];u2=[U(1);U(2);U(5);U(6)];u3=[U(3);U(4);U(5);U(6)];
% 计算单元应力
sigmal=PlaneTrussElementStress(E,L1,0,u1);sigma2=PlaneTrussElementStress(E,L2,theta2,u2);sigma3=PlaneTrussElementStress(E,L3,theta3,u3);
运行后的部分结果:
4 结论
实践证明,应用MATLAB软件解平面桁架问题简便、易行、通用,本文只是列举了一个简单的例子,对于求解复杂的平面桁架问题,本文介绍的方法同样适用。因此,我们倡议将MATLAB软件运用到教学里,让更多的学生了解并会用MATLAB软件求解力学问题,以便提高学生学习效率,激发学生学习兴趣。
参考文献
[1] P.I Kattan著,韩来彬译.MATLAB有限元分析与应用[M].北京:清华大学出版社,2004.
[2] 龙奴球,包世华. 结构力学I(第二版)[M].北京:高等教育出版社,2006.

