船体清刷机器人水动力阻力计算及其结构优化

黄东王成华徐宏水

（1.第七一五研究所，杭州，310023；2.哈尔滨工程大学机电工程学院，哈尔滨，150001）

（3.海军702厂，上海，200434)

船体清刷机器人水动力阻力计算及其结构优化

黄东1王成华2徐宏水3

（1.第七一五研究所，杭州，310023；2.哈尔滨工程大学机电工程学院，哈尔滨，150001）

（3.海军702厂，上海，200434)

对船体清刷机器人进行了水下阻力计算，首先确定机器人仿真所需要的数学模型和湍流模型，本文提出用RNG k-ε模型作为仿真的湍流模型，该模型不但增加了反映主流的时均应变率Eij，体现流体的流动情况和空间变化，有效提高计算精度，而且考虑了近壁面的湍流问题，提高了分析低雷诺数湍流的可靠性。利用Flunt软件计算出机器人在不同流速下的阻力，根据仿真结果对机器人结构进行了优化，改善了机器人的单方向阻力性能。

船体清刷机器人；水阻力；湍流模型；优化

大型船舶长期在水中航行，因此，会有大量的海洋生物（如海藻、藤壶、贝类等）附着在船体外表面[1-3]，它们一旦在船体表面附着便很难去除，也会对船体产生很大的危害。因此，船体清刷机器人具有极大的应用价值和市场潜力。

船体清刷机器人工作在水下，研究水下机器人的水动力学性能首先需要考虑机器人的水阻力性能，这不仅可以为机器人的快速行驶提供支持，而且也为其余的功能实现提供了保障。船体清刷机器人的外型阻力性能是研究周围流场对于其行走产生的阻碍作用，通过仿真计算选择合适的外型结构，改善机器人的单方向阻力性能。

1 阻力计算模型的建立

船体清刷机器人采用开放式框架结构，如图1所示，是水下机器的一种，因此，其结构按照水下机器人的基本布局进行设计，最大限度发挥各设备的技术性能，安装可靠方便、布置紧凑[4-6]。机器人采用有缆供能，动力比较充足。

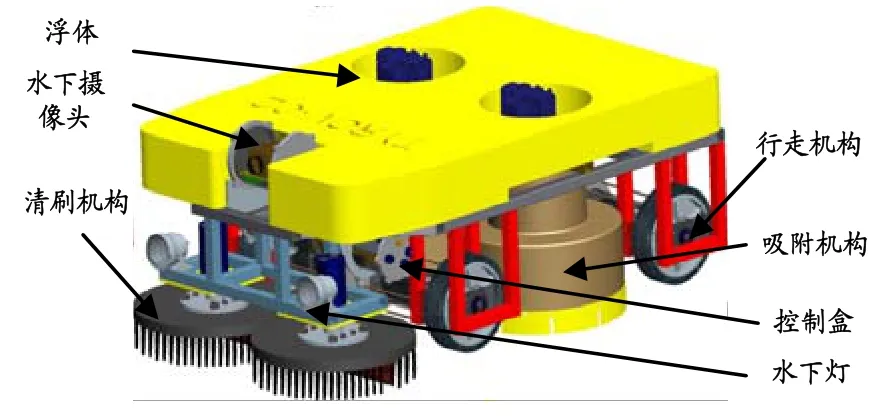
图1 船体清刷机器人三维模型

1.1 模型阻力计算流程

为分析图1中机器人外型结构的合理性和水下阻力的大小，采用Fluent软件仿真，用得到的结果进行验证。采用计算流体动力学（CFD）对机器人在水下的外型阻力的仿真过程见图2[7]。

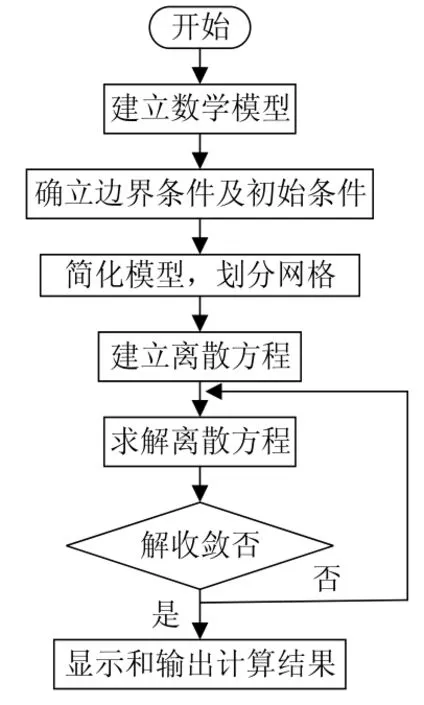
图2 外型阻力计算流程图

1.2 基本控制方程和湍流模型的选择

船体清刷机器人主体外型的分析也可理解为对其周围的湍流流场绕流的计算，流动都需要使用基本控制方程，这也是解决流体绕流问题的根本方程。适合于可压和不可压流动的质量守恒定律，其张量形式的方程为：

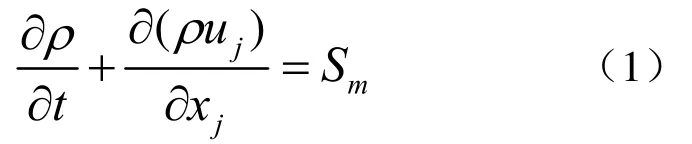
式中， ρ为液体密度；uj是沿着x坐标轴的速度分量；t为时间量；Sm是单位时间内液体质量的增加量。

在惯性坐标系下，i方向的动量守恒方程（又称为Navier-Stokes方程）的表达式如下：

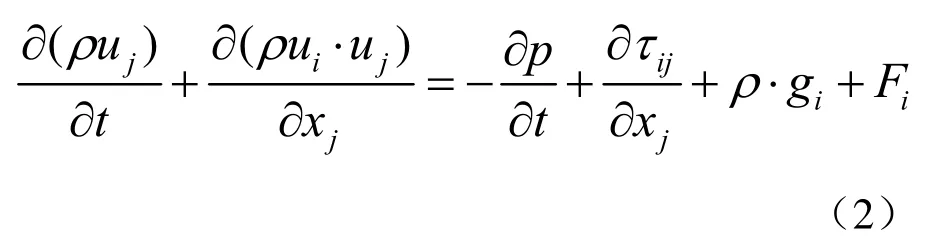
式中，p为单位流体上的静压力；gi是沿着x坐标轴的重力分量；iF为沿x轴线的外力分量；ijτ是粘性应力，其张量方程为：

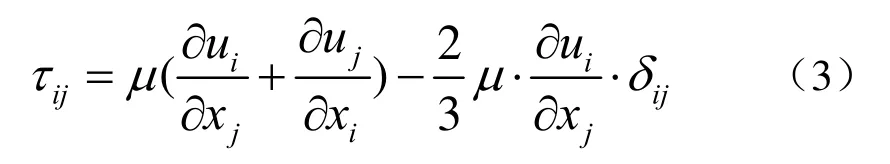
式中，μ为动力粘度；ijδ是“Kronecker delta”号（当i=j时，；当i≠j时，）。

由于船体清刷机器人的外型优化，不涉及到能量的交换问题，仅仅是对流体的阻力计算，因此，直接用质量守恒和动量守恒定律作为控制方程进行计算。

由于水下机器人的周围流场有明显的水流动荡，因此选择一个适当的湍流模型是非常有必要的。目前湍流的数值模拟方法中主要采用RANS方程法，忽略了密度的脉动变化问题，但体现出瞬态的脉动量，避免了需求的计算量过大。不可压流体时均脉动的NS控制方程如下[8-9]：

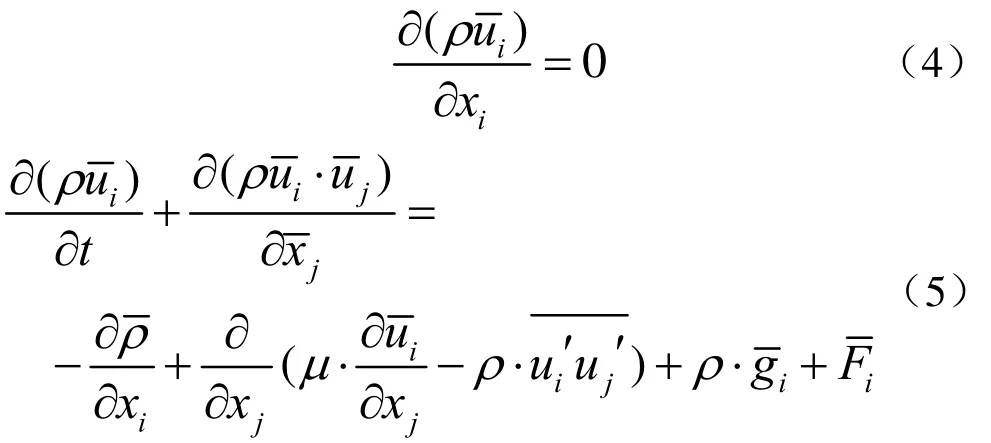
公式（4）为时均形式的连续方程，公式（5）为时均形式的雷诺方程。为湍流脉动值的雷诺应力项，反映了脉动速度引起的动量变化，建立雷诺应力关于湍动粘度的函数，即：

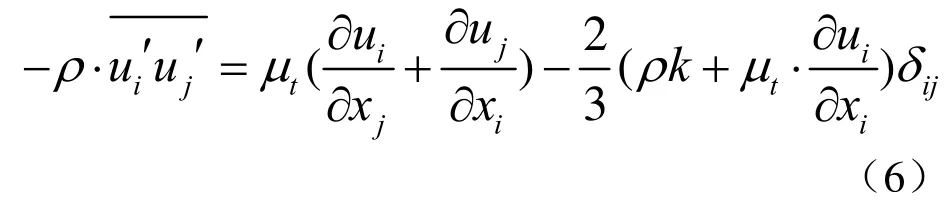
上式中，tμ即为湍动粘度，采用两个未知量来确定其关系式：

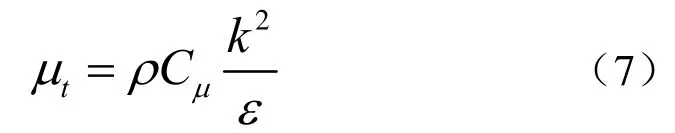
式中，Cμ是经验常数；k为湍动能量；ε是湍流耗散率。

由式（7）可知，湍动粘度采用k和ε两个变量来表示，即k−ε两方程模型，对不可压流体，k−ε模型的参数方程：

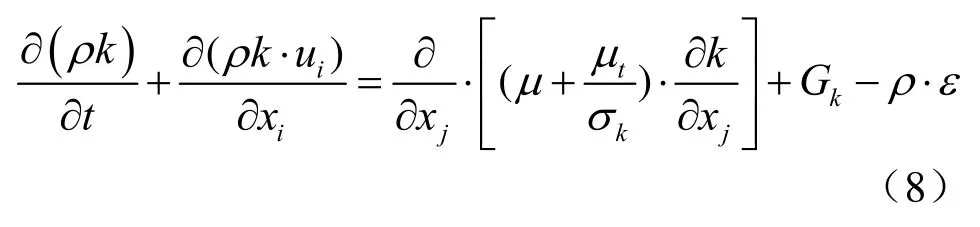
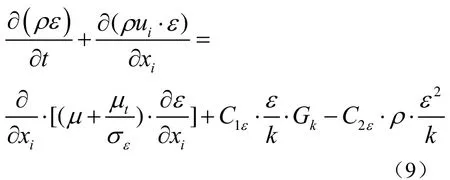
上面中k−ε两方程模型，都是基于湍流运动发展比较充分的条件下进行的，可以理解为适用雷诺数比较高的模型，但是船体清刷机器人是吸附在船体表面进行的工作，在接近船体部分的流动是低雷诺数或者是层流运动，湍流脉动的作用要远远低于水中粘性力的影响。采用标准的k−ε模型会出现结构的误差较大，因此，提出一种改进的k−ε模型，即RNGk−ε模型。两个变量方程为：

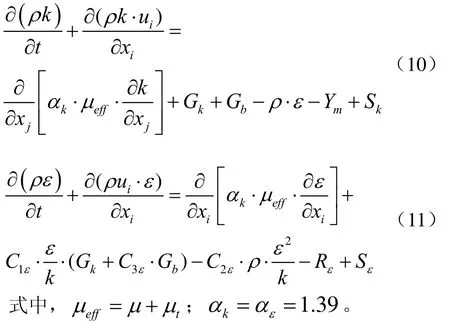
2 计算模型的简化及网格划分

由于该水下机器人形状比较复杂，而且构件比较多，直接将其导入到Meshing 14.5中进行网格划分难度较大，花费时间较多，进行阻力计算的工作量也很大。在机器人结构中有些元件的阻力较小，对于本身的流体性能影响不大。因此，在保证流体分析结果的前提下，将船体清刷机器人的模型简化为如下图3所示机器人简化模型[10]。

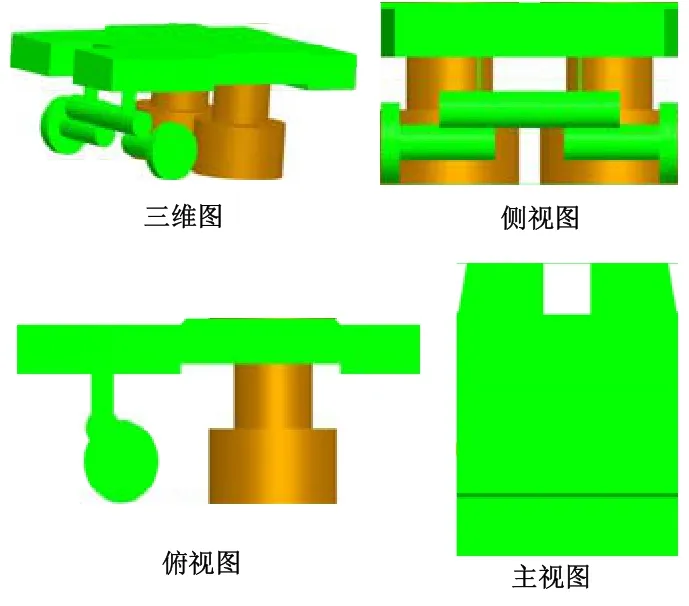
图3 船体清刷机器人的计算模型

计算域流场一般采用标准的长方体或者圆柱体，该机器人的计算域采用长方体，各个平面都沿着坐标轴方向。船体清刷机器人的计算域如图4所示。

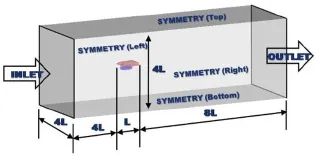
图4 船体清刷机器人的计算域流场

将水下机器人置于一个比自身长度稍大的小区域中。假设船体清刷机器人的流动方向上的长度为L=1 100 mm。

机器人主要受来流速度的影响，因此造成尾部的水动力学性能改变很大，为了真实模拟出尾部的水流，将长方体的后半部的长度加长。根据经验，机器人的后部计算域即从机器人的后侧到出口的长度为8L=8×1 100 mm =8 800 mm。同时，也为了避免其余壁面对水流造成的回旋影响，将长方体其余壁面的长度也加长。从入口处到机器人的主体前部的长度为4L=4 400 mm。计算域的高度和宽度是4L=4 400 mm。

划分网格是CFD仿真计算的第一步，主要分为结构化网格和非结构化网格两种形式。船体清刷机器人的曲面不是很多，故采用结构化网格对其进行划分。网格过少，会造成计算的精度过低，影响模拟结果的准确性，网格过多，增大计算机负担。因此，为了确保计算精度同时为了节省计算资源，采用不同的部分网格的划分数量不同。对于机器人的前部迎水的部分和控制盒进行细化网格，对于机器人的其余部分采用正常的网格划分。而对于机器人其余的计算域部分，越远离机器人的地方，网格尺寸越大，越靠近机器人模型的部分，网格尺寸越小。划分后的计算域网格如图5所示。

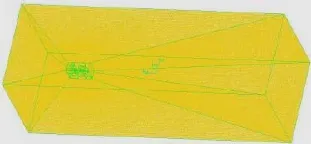
图5 计算域的网格划分

在机器人的计算域中主要采用六面体网格结构进行划分，在计算域的进出口附近网格尺寸大小为3 mm，六面体网格采用Tet/Hybrid类型。越靠近水下机器人的简化模型主体网格尺寸越小，大部分为0.5 mm，最大为2 mm。

通过使用ICEM CFD中的网格计算功能，计算出网格单元的数量，可以得到网格划分的单元为400万。船体清刷机器人附近的网格划分情况如下图6所示。

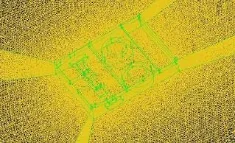
图6 船体清刷机器人的加密网格单元

网格的疏密程度对于仿真的结果和仿真数据准确性影响比较大。对于接受水流强度大的部分进行网格加密，有利于分析结果的准确性。对最终结果影响较小的部分如机器人的中间部分采用较疏的网格，既能提高计算精度，又能节省仿真的时间。在完成船体清刷机器人的计算域的网格划分后，为了求解出仿真模型的计算结果，即计算流体对机器人的阻力值，需要对初始条件和边界条件进行设定。

速度入口即Velocity-inlet边界条件

（1）使用k−ε模型对湍流进行计算，需要给定进口边界上的k和ε的估算值。对于没有任何已知条件的情况下，可根据下面公式粗略估计进口的k和ε的分布：

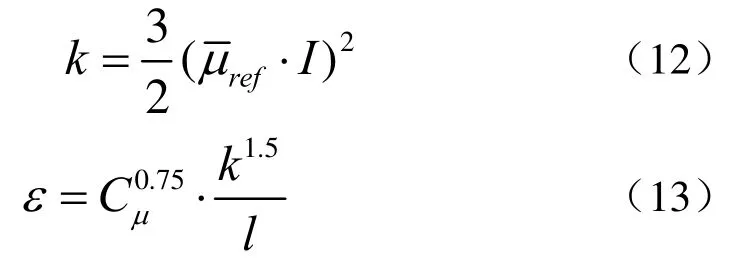
（3）洞室的爆破安全：洞室的爆破作业遵循一般爆破作业的安全规程；爆破作业时，要认真做好安全的警戒工作。人员撤至距工作面不少于200m的安全地点，施工机具撤至距工作面不少于100m的安全地点，难以撤离的施工机具和设备应加以妥善防护；本隧洞采用电力引爆，作业时，装炮时距工作面30m以内，断开电流，在30m以外用投光灯照明；在与相向开挖的贯通工作面相距30m放炮时，双方人员均撤离工作面，相距15m时停止一方工作，单向开挖贯通。

入口处湍流参数，按照公式（12）、（13）定义了湍流强度I和湍流长度尺度l。

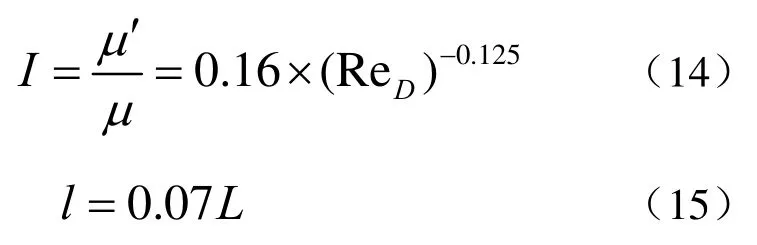
式中 为ReD机器人根据湍流直径得到的雷诺数；L为特征长度，即为机器人的长度。通过以上关系可以计算出入口的湍流参数如下：

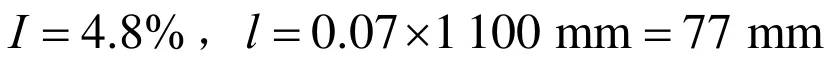
（2）出口边界条件：选择为自由出流口。

（3）固体壁面即Wall边界条件：机器人的所有表面都按照静止无滑移壁面进行设置，壁面粗糙度也均设置为0。

（4）池壁边界条件：按照默认值设置为无滑移壁面即可。

以进口速度的边界条件初始化整个计算域，初始条件只影响收敛速度而不会影响最终结果。

在ICEM CFD中将船体清刷机器人的网格划分后，将得到的网格文件导入到Fluent软件中进行数值和仿真分析。数值计算的离散方法采用了基于有限体积法的控制方程。离散格式采用基于压力变量的 SIMPLE 耦合求解器，采用一阶迎风差分离散格式，结合RNGk−ε两方程的湍流模型。

使用有限体积法离散控制方程，压力速度耦合方式采用Simple算法，压力釆用Standard离散，动量方程中的对流项采用First Order Upwind离散，湍流动能和耗散率方程也用First Order Upwind格式。虽然Second Order Upwind的优点在于求解精度比First Order Upwind格式高，但是数值计算收敛速度较慢，根据计算机的性能出发，选择了First Order Upwind格式。所有参数收敛残差设置为10−3，相关设置如表1所示。

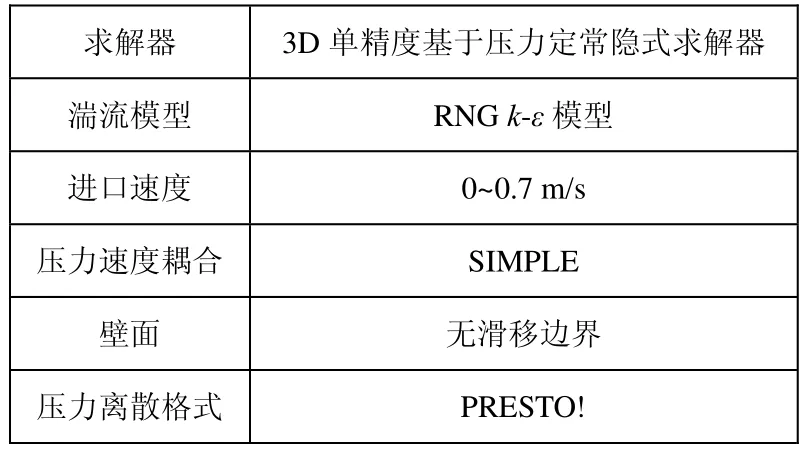
表1 仿真参数设置

3 机器人阻力结果分析及其优化

利用Fluent软件分析机器人在不同流速下的表面所受阻力，同时得到机器人表面受到的压力图，如图7所示。图中表示船体清刷机器人在最大流速为0.7 m/s时，从主视图、俯视图和侧视图三个角度看到机器人表面受到的压强分布情况。通过对上面压力分布图的分析可以得到模型较大正压强和较大负压强的位置。它显示出机器人的前部突出部位受到的正压强最大，而在凹进去的缺口处受到的负压强最大，轮子的前部受到的负压强也很大。其余部位的压强相对来说比较小。

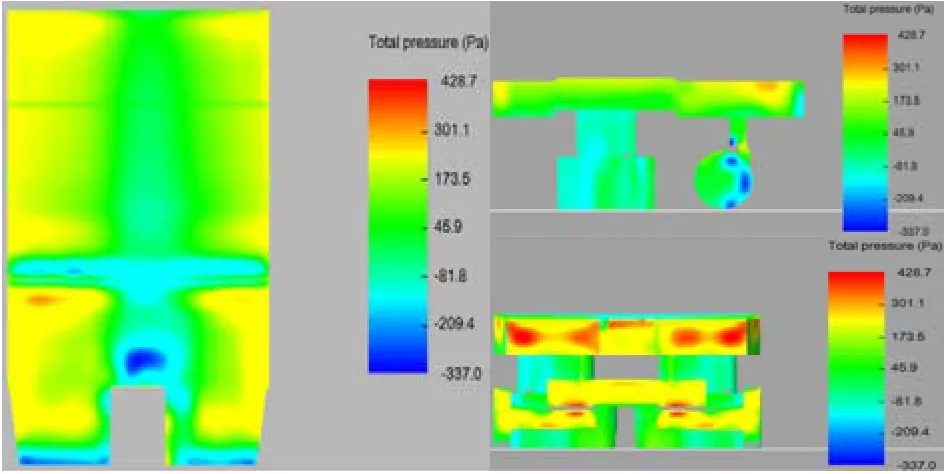
图7 机器人表面压力分布图

机器人的底部由于是圆柱形的元件，因此，受到较大的压强区域就是直接受到水流冲击的轮子前部，水流在这里会发生转弯和分离，因此，会在这里形成较大的负压区。之后，水流在流过两个大的圆桶时流速变化不大，故圆桶受到的压力比较小。上下表面的水流在机器人的尾部某个区域形成了汇合，形成一个汇合区。机器人的流线图如图8和9所示。

图8 机器人侧表面的流线图

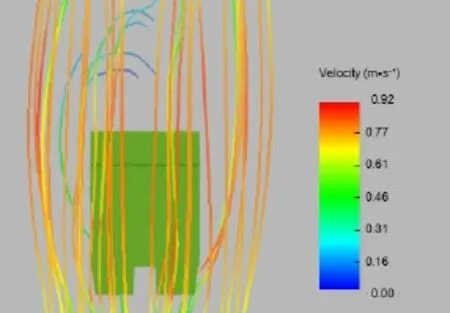
图9 机器人的俯视图的流线图

通过对机器人的水动力学仿真，得到压力分布图和流线图。在此基础上需要优化机器人的外型，以期达到减少阻力的目的。机器人的内部结构不易优化，但是浮体材料的外形对机器人的水动力学特性影响较大且能修改，可根据仿真结果对机器人外形进行优化。

从压力分布图中可知，机器人前部迎流的面积较大，因此将前部受到压强最大的位置改为半球形，减小受压面积，以减小机器人阻力。而且前部凹进去的位置会形成较大的负压区，为改变这种状况，也需要对这部分采用弧形优化，减少这部分受到最大阻力的面积，达到减少机器人总阻力的目的。另外，机器人的棱角容易形成负压，增大机器人阻力，所以对机器人的浮体外壳采取倒角的方式，使此处压力渐变，从而减少漩涡的形成，尤其是尾涡。优化后的浮体外壳增加了各部分的流线型，大大减少了阻力。经过优化后的外壳如图10所示。

图10 优化后的机器人浮体外壳

为了验证优化后的机器人的外壳阻力减少，同时，从阻力值中比较优化前后的好坏，分别将优化前和优化后的水下机器人进行仿真对比，阻力对比情况如图11所示。

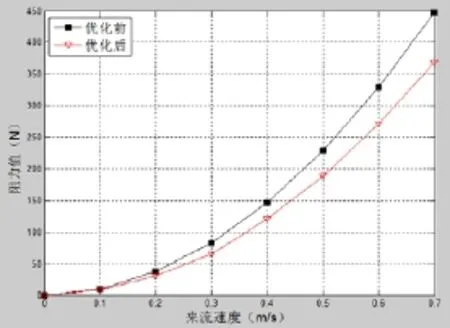
图11 优化前后阻力对比曲线图

随着来流速度的增加，阻力值逐渐增加，但是优化后的阻力增加较缓慢，当达到最大速度0.7 m/s时，优化前的阻力值为447.546 N，优化后的阻力值为368.229 N。因此，从仿真数据来说，达到了减少外型阻力的目的。

4 结论

通过对船体清刷机器人的水阻力性能的研究，优化了机器人的外形结构，明显地改善了机器人的水动力性能，当机器人达到最大速度0.7 m/s时，阻力减小了17.8%。船体清刷机器人的设计还处于初期阶段，本文的理论研究为以后机器人的改进提供一定的理论参照。未来在满足机器人功能的条件下，尽量做到机器人的小型化、产业化，为船舶的清刷作业提供快捷、方便的服务。

[1]兰志林，周家波.无人水下航行器发展[J].国防科技，2008,29(2):13-14.

[2]周凯，易杳甫.水下机器人概述和发展应用前景[J].科技向导，2010,24(4):283.

[3]付宜利，李志海.爬壁机器人的研究进展[J].机械设计，2008,25(4):1-5.

[4]常欣.Fluent船舶流体力学仿真计算工程应用基础[M].哈尔滨：哈尔滨工程大学出版社,2011:124-140.

[5]ARMADA M.Tele-presence and intelligent control for a legged locomotion robot[C]//Expert Systems and Robotics.Verlag,2001:377-396.

[6]BUDIYONO A.Advances in unmanned underwater vehicles technologies:modeling,control and guidance perspectives[J].Indian Journal of Marine Sciences,2009,38(3):282-295.

[7]尹龙.船体表面水下清刷机器人关键技术研究[D].哈尔滨工程大学，2004.

[8]CORFIELD S J,YOUNG J M.Unmanned surface vehicles-game changing technology for naval operations[J].IEE Control Engineering Series,2006:69-311.

[9]何漫丽.水下自航行器水动力学特性数值计算与试验研究[D].天津大学，2005:36-41.

[10]韩春生，何江青，王峰，等.水下船体表面清刷机器人磁吸附系统的研究[J].应用科技，2003,30(8):1-3.