线性变系数差分方程的时域求解方法

陈绍荣，刘郁林，朱桂斌，何 为

(1.重庆通信学院，重庆 400035；2.联合参谋部通信工程设计研究所，辽宁 沈阳 110005)



线性变系数差分方程的时域求解方法

陈绍荣1，刘郁林2，朱桂斌1，何 为1

(1.重庆通信学院，重庆 400035；2.联合参谋部通信工程设计研究所，辽宁 沈阳 110005)

以线性变系数微分方程的求解方法为依据，用类比法，提出了序列的原序列的概念，提出了后向差分运算对应的逆运算，即序列的不定求和，揭示了线性变系数差分方程的解结构。导出了一阶线性变系数差分方程的通解公式，基于一阶线性变系数差分方程的通解公式，利用降阶方法，导出了二阶线性变系数差分方程的通解公式，有效地解决了部分线性变系数差分方程的时域求解问题。

原序列；不定求和；变系数；差分方程；降阶法

在国内外《信号与系统》及《数字信号处理》的教材或文献[1-5]中，均提到线性离散时间系统可分为线性移变系统和线性移不变系统；在线性离散时间系统的时域分析中，都局限于介绍线性移不变系统的分析方法。其原因有两点，一是并非所有描述线性移变系统的线性变系数差分方程都有解；二是即使描述线性移变系统的线性变系数差分方程有解，由于缺乏数学理论基础的支撑和有效的方法，导致无法求出其解。本文提出了序列的原序列概念、序列的不定求和运算，揭示了线性变系数差分方程的解结构，导出了一阶线性变系数差分方程和二阶线性变系数差分方程的通解公式，有效地解决了部分线性变系数差分方程的时域求解问题。

1 数学理论基础

1.1 原序列

对定义在区间[n1，n2](n1、n2为整数)上的序列x(n)，若存在序列X(n)，对该区间[n1，n2]上的一切整数n满足

(1)

则称序列X(n)为序列x(n)在区间[n1，n2]上的原序列。

由原序列的定义，可得下述两个推论。

推论1：

若序列X(n)为序列x(n)在区间[n1，n2]上的原序列，则序列X(n)+C×1n(其中C为任意常数)也是序列x(n)在区间[n1，n2]上的原序列。

推论2：

若序列X(n)及Φ(n)均是序列x(n)在区间[n1，n2]上的原序列，则

Φ(n)-X(n)=C×1n

式中，C为任意常数。

1.2 序列的不定求和

若序列X(n)是序列x(n)在区间[n1，n2](n1、n2为整数)上的一个原序列，则序列X(n)+C×1n(其中C为任意常数)是序列x(n)在该区间[n1，n2]上的全体原序列，将一个序列x(n)的全体原序列(或原序列的集合)定义为序列x(n)的不定求和，记作∑x(n)，即

∑x(n)=X(n)+C×1n

(2)

(3)

式(3)表明，序列x(n)一阶后向差分后再不定求和，在还原出x(n)的同时，多出了一个任意的常数序列，特别地，如果取C=0，则式(3)描述的运算，仅还原出x(n)。因此，从本质上讲，序列的不定求和运算是序列后向差分运算的逆运算。

显然，由式(2)可以得到

(4)

式(4)表明，序列x(n)不定求和后再差分，其结果仍然是x(n)。

显然，序列的不定求运算还具有下述两个性质。

性质1：

∑Cx(n)=C∑x(n)

式中，C为任意常数。

性质2：

∑[x1(n)±x2(n)]=∑x1(n)±∑x2(n)

由序列不定求和的定义，我们可以得到下述3个常用的序列不定求和公式：

1)若a>0，则有

(5)

2)当a≠1时，则有

(6)

3)当a≠1时，则有

(7)

式中，u(n)为单位阶跃序列。

2 线性变系数差分方程的通解

2.1 一阶线性变系数差分方程的通解

这里将构建一阶线性变系数齐次差分方程的通解公式和一阶线性变系数非齐次差分方程的通解公式。

y(n)-v(n)y(n-1)=x(n)，v(n)>0

(8)

处理方式1：

利用常数变易法来确定一阶线性变系数非齐次差分方程式(8)的通解。

1)求一阶变系数齐次差分方程

y(n)-v(n)y(n-1)=0，v(n)>0

(9)

的通解。

由一阶变系数齐次差分方程式(9)可得

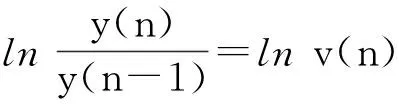
亦即lny(n)-lny(n-1)=lnv(n)

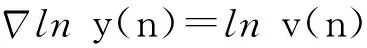
(10)

对式(10)两边作不定求和可得

考虑到式(3)，则上式可写成

lny(n)=C1×1n+∑lnv(n)

那么，一阶变系数齐次差分方程式(9)的通解公式为

y(n)=eC1×1n+∑lnv(n)=Ce∑lnv(n)

(11)

式中，C1和C=eC1均为任意常数。

2)设一阶变系数非齐次差分方程式(8)的通解为

y(n)=C(n)e∑lnv(n)

(12)

考虑到式(12)，则有

y(n-1)=C(n-1)e∑lnv(n-1)

(13)

将式(12)及式(13)代入一阶变系数非齐次差分方程式(8)，并考虑到式(4)，则有

(14)

对式(14)两边作不定求和可得

考虑到式(3)，则上式可写成

C(n)=C×1n+∑x(n)e-∑lnv(n)

那么，一阶变系数非齐次差分方程式(8)的通解公式为

y(n)=C(n)e∑lnv(n)=[C×1n+∑x(n)e-∑lnv(n)]e∑lnv(n)

(15)

式中，C为任意常数。

处理方式2：

考虑到

y(n)-v(n)y(n-1)=x(n)，v(n)>0

(16)

将式(16)两边乘e-∑lnv(n)可得

y(n)e-∑lnv(n)-elnv(n)-∑lnv(n)y(n-1)=x(n)e-∑lnv(n)

考虑到式(4)，则上式可写成

即

y(n)e-∑lnv(n)-e∑lnv(n)-∑lnv(n-1)-∑lnv(n)y(n-1)=x(n)e-∑lnv(n)

y(n)e-∑lnv(n)-e-∑lnv(n-1)y(n-1)=x(n)e-∑lnv(n)

(17)

对式(17)两边作不定求和可得

考虑到式(3)，则上式可写成

y(n)e-∑lnv(n)=C×1n+∑x(n)e-∑lnv(n)

那么，一阶变系数非齐次差分方程式(8)的通解公式为

y(n)=[C×1n+∑x(n)e-∑lnv(n)]e∑lnv(n)

(18)

式中，C为任意常数。

结论1：

由一阶线性变系数非齐次差分方程的通解公式(15)或(18)可知，一阶线性变系数非齐次差分方程式(8)的解结构为

(19)

式中，C为任意常数。

2.2 高阶线性变系数差分方程的通解

对于高阶线性变系数非齐次差分方程，可以利用降阶的方法转化成一阶线性变系数非齐次差分方程来进行研究。

y(n)-[v1(n)+v2(n)]y(n-1)+v1(n)v2(n-1)y(n-2)=x(n)

(20)

式中，v1(n)>0，v2(n)>0。

其实，二阶线性变系数非齐次差分方程式(20)可写成

y(n)-v2(n)y(n-1)-v1(n)[y(n-1)-v2(n-1)y(n-2)]=x(n)

(21)

记y(n)-v2(n)y(n-1)=w(n)

(22)

那么，二阶线性变系数非齐次差分方程式(21)可写成

w(n)-v1(n)w(n-1)=x(n)

(23)

由式(23)，并考虑到式(19)，则有

w(n)=C1e∑lnv1(n)+e∑lnv1(n)∑x(n)e-∑lnv1(n)

(24)

考虑到式(24)，则式(22)可写成

y(n)-v2(n)y(n-1)=w(n)=C1e∑lnv1(n)+e∑lnv1(n)∑x(n)e-∑lnv1(n)

(25)

由式(25)，并考虑到式(19)，则有

y(n) =C2e∑lnv2(n)+e∑lnv2(n)∑w(n)e-∑lnv2(n)=C2e∑lnv2(n)+e∑lnv2(n)∑[C1e∑lnv1(n)+ e∑lnv1(n)∑x(n)e-∑lnv1(n)]e-∑lnv2(n)

(26)

式中，C1和C2为任意常数。

结论2：

由二阶线性变系数非齐次差分方程的通解公式(26)可知，二阶线性变系数非齐次差分方程式(20)的解结构为

(27)

3 例题分析

例1：若一阶线性变系数差分方程为

y(n)-ny(n-1)=2nn!u(n)，试求其通解。

解：因为v(n)=n，x(n)=2nn!u(n)，由式(19)，并考虑到式(7)，则有

y(n) =Ce∑lnv(n)+e∑lnv(n)∑x(n)e-∑v(n)=Ce∑lnn+e∑lnn∑2nn!u(n)e-∑v(n)=Celnn!+elnn！∑2nn!u(n)e-lnn!=Celnn!+elnn！∑2nu(n) =Cn!+(2n+1-1)n！u(n)

式中，C为任意常数。

例2：若一阶线性变系数差分方程为

对上式作不定求和可得

考虑到式(3)及式(7)，由上式可得

y(n)=Cn2！+(2n+1-1)n2！u(n)

式中，C为任意常数。

例3：若一阶线性变系数差分方程为

y(n)-4ny(n-1)=2n2+2n，试求其通解。

解：考虑到y(n)-4ny(n-1)=2n2+2n

则y(n)2-n(n+1)-2-(n-1)ny(n-1)=2n

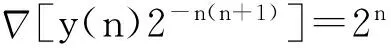
对上式作不定求和可得

考虑到式(3)及式(6)，由上式可得

y(n)2-n(n+1)=C×1n+2n+1y(n)=C×2n(n+1)+2(n+1)2

式中，C为任意常数。

例4：设二阶线性变系数差分方程为

y(n)-3×4-ny(n-1)+8×16-ny(n-2)=2n-n2u(n)

若y(-2)=2，y(-1)=12，试求y(n)。

解：方法1：

考虑到

y(n)-3×4-ny(n-1)+8×16-ny(n-2)=2n-n2u(n)

则有

y(n)-4-ny(n-1)- 2×4-n[y(n-1)-4-(n-1)y(n-2)]=2n-n2u(n)

将上式两边乘2n2可得

[y(n)-4-ny(n-1)]2n2- [y(n-1)-4-(n-1)y(n-2)]2(n-1)2=2nu(n)

对上式两边作不定求和可得

考虑到式(3)及式(7)，由上式可得

即y(n)-4n-y(n-1)=C12-n2+2-n2(2n+1-1)u(n)

将上式两边乘2(n+1)n可得

y(n)2(n+1)n-y(n-1)2n(n-1)=C12n+(2×4n-2n)u(n)

对上式两边作不定求和可得

考虑到式(3)、式(6)及式(7)，由上式可得

式中，C1和C2为待定系数。

方法2：

令v1(n)=2×4-n=21-2n，v2(n)=4-n，

x(n)=2n-n2u(n)

考虑到式(5)，则有

由式(27)，并考虑到式(6)及式(7)，则有

式中，C1和C2为待定系数。

于是，有

4 结束语

本文用类比法，通过与线性变系数微分方程的求解方法相比较，提出了序列的原序列概念、序列的不定求和运算，给出了3个常用序列的不定求和公式，揭示了线性变系数差分方程的解结构。同时，还导出了一阶线性变系数差分方程和二阶线性变系数差分方程的通解公式，有效地解决了部分线性变系数差分方程的时域求解问题。

[1] 张有正.信号与系统[M].成都：四川科技出版社，1985.

[2] 郑君里.信号与系统[M].北京：高等教育出版社，1981.

[3]SolimanSS，SrinathMD.Continuousanddiscretesignalsandsystems[M].london：PrenticeHall，1990.

[4] 奥本海姆AV，谢弗RW，巴克JR.离散时间信号处理处理[M].刘树棠，黄建国，译.西安：西安交通大学出版社，2001.

[5] 胡广书.数字信号处理—理论、算法与实现[M].3版.北京：清华大学出版社，2012.

[6] 陈绍荣，刘郁林，雷斌，等.数字信号处理[M].北京：国防工业出版社，2016.

A Study on the Solutions of Time Domains of Linear Difference Equations With Variable Coefficients

CHEN Shaorong1，LIU Yulin2，ZHU Guibin1，HE Wei1
(1．Chongqing Communication College of PLA，Chongqing 400035，P.R.China；2．Communication Engineering Design Institute of the Joint Staff of the Central Military Commission of CPC，Shenyang Liaoning 110005，P.R.China)

Based on the solutions of linear differential equations with variable coefficients，by means of the method of analogy，this paper introduces the concept of original sequences of sequences as well as inverse operations corresponding with backward difference operations，that is， indefinite summations of sequences，which reveal the structures of solutions of linear difference equations with variable coefficients．In addition，the general solution formulas for first-order linear difference equations with variable coefficients can be derived．Based on the formulas，depending on the method of the reduction of order，the general solution formulas for second-order ones can be derived as well，which are effective in the solutions of time domains of some linear difference equations with variable coefficients．

original sequences；indefinite summations；variable coefficients；difference equations；method of the reduction of order

2016-11-03

陈绍荣(1963-)，副教授，研究方向为信号处理。

O241；TN911.7

A

1008- 8032(2016)06- 0038- 05

该文获重庆市电机工程学会2016年学术年会优秀论文一等奖