不均匀沉降下半刚性连接钢框架附加内力分析

屈敦文, 胡曼莉

(1. 苏州科技大学 土木工程学院, 江苏 苏州215011; 2. 多维联合集团有限公司, 北京 100190)

不均匀沉降下半刚性连接钢框架附加内力分析

屈敦文1, 胡曼莉2

(1. 苏州科技大学 土木工程学院, 江苏 苏州215011; 2. 多维联合集团有限公司, 北京 100190)

在钢框架设计计算中, 一般假设梁柱节点为完全刚性或者理想铰接, 但在实际工程中理想铰接与完全刚接是不存在的, 梁柱节点为介于铰接、刚接之间的半刚性连接结构. 考虑到梁柱半刚性连接, 对结构受力性能会产生较大影响,运用结构力学方法结合半刚性连接梁单元的转动刚度和传递系数, 推导不均匀沉降下框架附加内力. 并利用SAP2000有限元计算软件, 分析工程实例, 将手算与电算结构进行对比, 得到的计算实例表明: 此计算方法快速、便捷, 可用于初步计算不均匀沉降下大跨度钢框架附加内力.

半刚性连接; 支座不均匀沉降; 钢框架; 附加内力

引言

钢框架这样的结构形式在实际工程中屡见不鲜, 结构设计应该根据结构受力性能来确定计算模型并进行分析计算. 尤其是梁柱节点的选择, 将对受力性能准确性造成较大的影响. 在钢框架设计中, 为了计算方便, 一般若结构转动约束达到完全刚接的90%则视该节点为刚接; 当结构转动达到理想铰接的80%则视该节点为铰接. 而实际工程中梁柱节点必定处于铰接、刚接之间的半刚性连接结构方式[1].梁柱节点刚度的选定很大程度上会影响结构内力, 不仅会引起内力重分布, 也会加大二阶效应与层间位移. 故将半刚接节点盲目假设成完全刚接或铰接, 其结果明显不安全. 而在初步设计阶段, 为了快速清晰地明确结构布置方案, 需要进行简单明了的手算. 因此要求手算应概念明确, 直观反应出钢框架受力特点.

文[2]详细介绍了半刚性连接钢框架的简化计算模型与方法, 本文基于此计算模型与方法, 选取某实际工程空间框架简化的平面框架, 在柱脚施加不均匀沉降, 计算不同于全部刚接或者完全铰接的半刚性梁柱连接方式, 并运用结构力学方法求出半刚性上部钢框架附加内力手算公式. 附加内力其实是上部结构在支座变形时相对于未变形时的调整量, 得到的附加内力手算公式, 可为初步设计提供依据.

1 半刚性连接

本文题材来自苏州中心8号9号高层2层到4层的钢框架连廊, 该钢框架梁柱节点采用摩擦型高强螺栓外伸端板连接. 该梁柱节点在框架发生变形时, 既有一定的相对转动, 又能传递一定弯矩, 故为典型的半刚性连接. 本文的计算实例即采用该连廊平面简化模型, 梁柱之间连接主要是作用于传递构件之间的轴力、剪力、弯矩和扭矩. 平面框架忽略扭动的影响, 并且由于受力所引起的轴向、剪切、与转动变形不是很大. 因此只考虑连接时转动变形.

2 转动刚度与传递系数

框架刚度系数是需解决的基本问题, 对于半刚性框架在内力分析时, 需要得到其转动刚度和传递系数. 图1为由三参数模拟半刚性连接节点弯矩—转角曲线图得到的梁有效刚度的示意图, 有效刚度计算式为

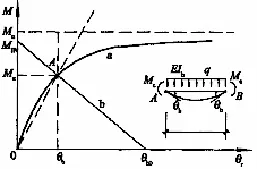
图1 半刚性连接有效刚度

图1 中a为三参数模拟的半刚性节点弯矩—转角曲线.MFA为钢梁在竖向荷载下完全刚接时得到的固端弯矩,θb0为梁完全铰接时得到的梁端转角. 在图1中, 找到(0,MFA)与(θb0, 0)这两点将其连接成直线b, 曲线a与直线b的交点A处即为该梁柱节点的有效刚度.

从图1中同样可以得出初始刚度和初始割线刚度具有相同的初始转角. 为了便于理论推导, 进行简化运算, 故取一定刚度、长度不计的弹簧模拟梁柱节点的连接, 用M=Kr×θr表示转角弯矩, 其中Kr为弹簧刚度的初始割线刚度即为有效刚度,θr为梁柱节点的相对转角. 令梁刚度与弹簧刚度比值为, 其中EI为梁的抗弯刚度,L为梁的跨度,i为梁线刚度. 由于实际工程中梁柱节点必b为处于铰接、刚接之间的半刚性连接结构方式, 故应该对梁的刚度进行修正. 利用结构力学位移法可知一端半刚性连接, 一端铰接梁单元的转动刚度, 传递系数为0[2,3].

3 不均匀沉降下钢框架附加内力推导

3.1 假定条件

在研究不均匀沉降对框架产生的附加内力时,作以下假设:

(1) 对于层高不高的钢框架不考虑柱的轴向变形, 柱长恒定, 每一层梁柱节点的竖向位移与柱脚的竖向位移一致. 上层柱反弯点在层高处, 底层柱反弯点在距柱底处, 梁的反弯点统一为跨中处.

(2)有限元模型材料均假定为线弹性材料, 非线性变形以及上下不同层梁的相互作用均不考虑, 并假定沉降发生时, 钢架无水平侧移.

图2 半刚性大跨度钢框架

由于结构对称以及对柱反弯点所作的假定, 只取一半结构进行分析.

图3 计算单元

3.2 附加内力推导

以图2的两层一跨半刚性连接钢框架为例, 计算梁端附加弯矩和附加剪力, 假定上柱线刚度取icu, 下柱线刚度取. 故上层柱刚度取2, 下层柱取. 根据假定条件, 可将钢框架分解为图3所示的两半跨计算单元, 同时假定不均匀沉降在每层梁处引起一个θ转角, 用Mi表示梁端弯矩; 用Mizu表示上层柱端弯矩,Mizl表示下层柱端弯矩. 弯矩以顺时针为正, 根据计算简图以及结构力学方法得:

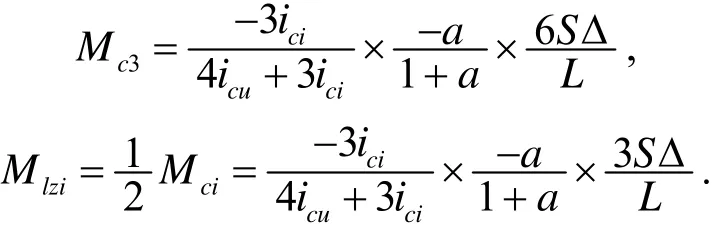
4 实例验算与分析

4.1 实例验算

某钢框架总高17.2m,首层高11.94m, 二层高5.26m.柱截面为H1000×500×35× 50, 梁截面为H1000×500×22×32. 钢材的弹性模量为E=2.8× 104N/mm2. 由以上参数可得:

梁线刚度ib=0.65× 1010N.mm ; 柱线刚度icu=3.15× 1010N.mm ,icl=1.39× 1010N.mm.

假定半刚性梁柱节点模型中弹性刚度为1.0× 1010N.mm, 则α=1.3,可得.

根据GB5007-2011中《建筑物地基变形允许值》的规定, 故假定Δ= 200mm.

计算结果见表1.

表1 不均匀沉降下内力值手算结果

通过计算可得柱脚弯矩

将计算简图在sap2000中建模, 求解其在不均匀沉降下得到的附加轴力、剪力与弯矩, 结果见表2.

表2 不均匀沉降下内力值电算结果

通过电算可得柱脚弯矩

手算与电算之间的误差见表3.

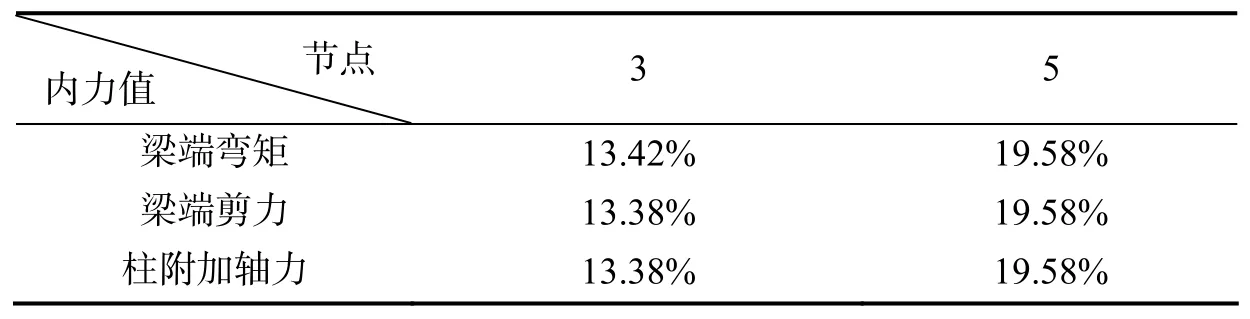
表3 手算与电算之间的误差

4.2 误差分析

手算近似解是在空间框架计算模型进行简化之后, 结合基本假定与结构力学方法, 得出的附加内力.这样的方法较为简单, 抓住了该结构的特点, 但是模型简化过程以及结合机构力学方法较为粗糙. 而SAP2000有限元计算软件主要是对体系进行精确网络划分, 利用结构刚度矩阵, 将单元矩阵转化为整体矩阵, 并利用平衡关系求出结构相应的内力值. 从模型建立到划分、计算等过程较为精细, 但是有限元软件通过迭代方法较为复杂, 不太适合手算. 在结构初步设计阶段, 需要手算方法简单、快速、清晰地反映结构受力特点及主要影响因素. 从表3误差表格中可以看出两种方法的值误差都小于20%, 上层的误差显著大于下层, 原因在于理论推导假定中, 没有考虑柱轴向变形对结构内力重分配的影响, 同时二阶效应的加强, 使得误差会更加大. 所以随着沉降值以及半刚性结点刚度比的变化, 内力值也会随之变化.

5 结语

通过以上的计算分析, 得出以下结论:

(1) 理论近似的手算方法, 主要是基于多项假定以及结构简化, 并结合结构力学方法, 从而得到其附加内力值. 对于结构初步设计来说, 它具有快速、便捷的特点, 但是其结果较粗糙.

(2) 由于在公式推导的过程中, 假定不考虑柱轴向变形, 使得结果趋于保守, 具有一定安全性. 但是结构在实际受力中, 必定出现柱的轴向变形, 内力重分布以及二阶效应. 故当结果需要更加精确时应当考虑轴力引起柱的变形.

(3) 该计算方法可用于初步计算不均匀沉降下大跨度钢框架附加内力.

(4) 为了提高该计算方法的精确性, 可进一步考虑柱轴向变形对该计算方法的影响, 即采用迭代方法,逐步求出在考虑柱轴向变形下不均匀沉降半刚性连接钢框架附加内力. 并进一步找到解决迭代计算过于复杂的方法.

[1] 贺润丰. 半刚性钢框架结构分析设计现状及发展分析[J]. 中华民居, 2013,12: 206～208

[2] 胡习兵, 舒兴平, 沈蒲生. 半刚性连接钢框架的简化计算方法[J]. 湖南大学学报: 自然科学版, 2005, 8(4): 18～23

[3] 杜加清, 夏军武. 半刚性钢框架竖向跨间刚度计算[J]. 黑龙江科技学院学报, 2012,3(2): 199～201

[4] 龙驭球, 包世华. 结构力学[M]. 北京: 人民教育出版社, 1983: 262～400

[5] 朱延章, 潘志宏. 半刚性连接钢框架基于极限状态的抗震设计[J]. 钢结构, 2016(8): 1～7

[6] KISHIN, GOTO Y, CHEN W F, et al.Applicability of three parameter power model to structural analysis of flexibly jointed frames[J]. Mechanics Computing,1991, 20(3): 238～242

Accessional Internal Force Analysis of Semi-rigid Connections Steel Frames Under Differential Settlement

QU Dunwen1, HU Manli2
(1. Department of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China; 2. Duowei Union Group, Beijing 100190, China)

In the steel frame design and calculation, it is assumed that beam-column joints are completely rigid or ideal hinges. But the ideal hinge and completely rigid does not exist in practical projects. Beam-column connections are the semi-rigid joints between the hinge and the rigid. Considering the semi - rigid connections, the structure will have a greater impact on mechanical properties. The rotational stiffness and transfer coefficient of the semi - rigid beam element were derived by using the structural mechanics method, and the accessional internal force of the frame under differential settlement was deduced. The SAP2000 finite element calculation software was used to analyze a engineering example, and compare the hand calculation with the computer calculation.The results showed that the method is fast and convenient, and it can be used to calculate the accessional internal force of large - span steel frame under different settlement.

semi-rigid connection, differential settlement, steel frame, accessional internal force

TU328

: A

: 1672-5298(2016)04-0064-05

2016-10-17

屈敦文(1992− ), 男, 湖南郴州人, 苏州科技大学土木工程学院硕士研究生. 主要研究方向: 混凝土结构与组合结构