基于改进朴素贝叶斯的入侵检测方法*
孙 程,邢建春,杨启亮,韩德帅
(解放军理工大学 国防工程学院,江苏 南京 210007)
基于改进朴素贝叶斯的入侵检测方法*
孙 程,邢建春,杨启亮,韩德帅
(解放军理工大学 国防工程学院,江苏 南京 210007)
工业控制系统的网络安全问题越来越严峻,遭到的入侵威胁也越来越复杂。伴随着网络的开放性、复杂性不断增强,入侵威胁正在不断加深。为了抵御愈趋复杂和多样的入侵威胁,需要设计高效的入侵检测方法。朴素贝叶斯分类算法是一种有效而简洁的分类算法,能较好地应用于工业控制系统网络的入侵检测。但是它的属性独立性假设使得该方法无法表示属性变量之间存在的关系,影响了它的分类效果。针对该缺陷,借鉴前人的经验,提出了一种改进综合加权系数的朴素贝叶斯分类算法(Compositive Weighted Naive Bayes Classification,CWNBC)。该算法既考虑了不同属性取值对分类结果的影响,又考虑了属性值的内容对分类的影响,巧妙地引入了综合加权系数。将该算法与其他几种算法比较,经实验表明,该分类算法有较高的分类准确率,能更好地适用于比较复杂的工业控制系统网络的入侵检测。
朴素贝叶斯;加权系数;属性值
0 引言
网络技术的飞速发展在给人们的生活带来极大便利的同时,也给人们带来了较大的安全威胁。随着网络的开放性和复杂性不断增强,工业控制系统(Industry Control System,ICS)面临的安全问题也日益凸显,遭到的入侵威胁不断增大。
入侵检测是ICS的网络安全防御中重要的组成部分,是保护系统安全的重要手段,一直被国内外专家学者所关注。入侵检测技术是一种要找出能够危害信息资源完整性、机密性和可用性的安全措施[1]。入侵检测的目的是在海量的未知网络事件数据中,将正常事件(Normal)和异常事件(Anomaly)精确分类,达到发现网络攻击事件和降低误报警率的目的[2]。入侵检测技术一般可分为两种:误用检测和异常检测。误用检测指的是根据已知的攻击方法来预先定义入侵模式,通过判断这些入侵模式是否会出现来完成检测任务。误用检测的缺点在于其局限于已有知识的检测范围,不能检测出已有知识之外的攻击行为。异常检测指的是根据资源的使用状况或使用者的行为来判断是否遭到入侵,而不是依据具体的行为是否出现作为检测的标准,相对而言,异常检测的适用性比较强,可以检测出陌生的攻击行为,不像误用检测那样受限于已知的攻击手段,其主要的缺陷是误检率较高,尤其在用户较多、工作条件、系统参数、网络结构等各种因素时常变化的环境中[3-5]。目前,有较多的有效的入侵检测分类模型被提出。如文献[6]提出了结合误用检测与异常检测的混合入侵检测模型,文献[7]提出了结合网络协议分析技术和决策树挖掘技术的一种新型模型,文献[8-10]将其他学习算法运用于入侵检测中,如支持向量机、遗传算法、人工神经网络等。
为了提高朴素贝叶斯分类器的性能,使其能更好地适用于ICS网络的入侵检测,基于前人的研究,本文提出了一种改进综合加权系数的朴素贝叶斯分类算法(Competitive Weighted Naive Bays Classification,CWNBC),该算法是在传统的朴素贝叶斯分类模型的基础上加入了综合加权系数,该综合加权系数融合了协方差理论与文献[11]提出的加权系数,这弥补了文献[11]仅考虑属性的频数关系,而忽略了属性值的内容对分类的影响这一不足之处,使文献[11]中原本简洁高效的算法更加完善。
1 朴素贝叶斯分类算法
朴素贝叶斯分类算法是一种较为简单而且有效的分类方法,它以贝叶斯定理作为理论基础,其性能与神经网络、决策树等应用较广的算法相当,在某些领域中甚至可表现出更优越的性能[12-13]。
朴素贝叶斯分类算法的分类原理是根据某个对象的先验概率计算出其后验概率,后验概率最大的类则为该对象所属的类。其工作流程如下:
(1)用特征向量来表示每个数据样本。
(2)对原始数据样本X进行分类, 一般把X划分到后验概率值最大的类, 本质上就是求P(Ci|X)的最大值。即:
(1)
(3)要求P(Ci|X)的最大值,只需使P(X|Ci)P(Ci)最大化即可。如果不知道先验概率,一般认为它们是等概率的,即P(C1)= P(C2)=…=P(Cn)。否则,可根据概率学的知识由先验概率公式计算出:
(2)
其中,Si为训练样本数,S为训练样本总数。
(4)在属性集的属性数比较多的情况下,为了减少计算时间,一般假设类条件相互独立,即各个属性值之间相互独立。
(3)
若Ak是离散属性,可由式(4)计算出概率:
(4)
其中,Sik表示属性Ak的取值为xi且属于类Ci的训练样本的数目,而Si则表示类Ci中的训练样本的总数。
若Ak为连续属性,一般认为它是属于高斯分布的。
(5)对X进行分类,需要计算每个类Ci的P(X|Ci)P(Ci),如果样本X被分到类Ci,则需满足如下条件:
P(X|Ci)P(Ci) >P(X|Cj)P(Cj),1≤j≤m,j≠i
(5)
其中m为类的总数。换言之,使P(X|Ci)P(Ci)获得最大值的类Ci即为X所属的类。
2 加权朴素贝叶斯分类算法
虽然朴素贝叶斯分类算法应用简单,分类准确率相对较高,预测和学习的时间小于其他分类算法,但该算法有个理想的假设,其假设每个属性对给定类的影响独立于其他的属性,而在现实中此假设是很难满足的。因此,为了弥补该不足之处,研究人员先后提出多种加权朴素贝叶斯分类算法[14]。
人们试图将朴素贝叶斯分类算法与属性加权算法相结合,根据各属性对分类影响的大小赋予不同的权重系数,以此来提高朴素贝叶斯分类算法的准确率。文献[15]提出基于分类概率的朴素贝叶斯分类算法,使用朴素贝叶斯分类成功的概率作为加权系数;文献[16]提出基于粒子群算法的WNBC算法, 通过粒子群算法的自动搜索功能对现有数据和信息进行学习, 以数据集中所有数据各自权重的平均值作为加权系数;文献[11] 提出根据不同的属性取值对分类结果的影响来设定加权系数;文献[14]中分别采用爬山算法、信息增益和蒙特卡罗技术来确定属性的权值等。
3 改进综合加权朴素贝叶斯算法
3.1协方差属性加权系数
在实际应用中,事物的不同属性对事物分类的影响是不同的,根据属性的影响程度分为条件属性和决策属性。决策属性指的是对分类有显著影响的属性。条件属性指的是剩余的其他属性。此外,不同的条件属性与决策属性的相关程度也是不同的。由决策属性X和条件属性Y组成的系统ρ反映了属性X和Y的相关紧密度,ρ越大表明条件属性Y对决策属性X的影响越大,反之亦然。属性之间的相关系数公式为:
(6)
为了确保权重系数为正,则设定权值为:
(7)
3.2 改进综合加权系数
通过对比以上多种方法,结合文献[11]中提出的根据不同的属性取值对分类结果的影响来设定加权系数的思想,本文提出了一种新的权值计算方法。
设NAk表示属性Ak的取值个数,N(Ak=m)表示属性Ak取值为m的样本对象的个数, N(Ak=m∩Ci)表示属性Ak取值为m且属于类Ci的样本对象个数。根据各属性的不同取值对分类的影响设计权值, 加权系数公式表示为:
(8)
虽然式(8)根据每个属性的不同取值对分类的影响计算权值, 但其考虑的是属性值的频数关系,没有考虑属性值的内容对分类的影响。协方差理论主要利用属性值的内容来表达属性之间的关联,因此把这两种方法融合起来,会得到更加合理准确的加权系数。
3.3 基于CWNBC的入侵检测算法
从本质上来说,入侵检测的目的就是设计一个分类器,把收集到的数据信息分为正常和异常两大类,然后对异常的数据进行分析处理。基于CWNBC的入侵检测流程如图1所示。
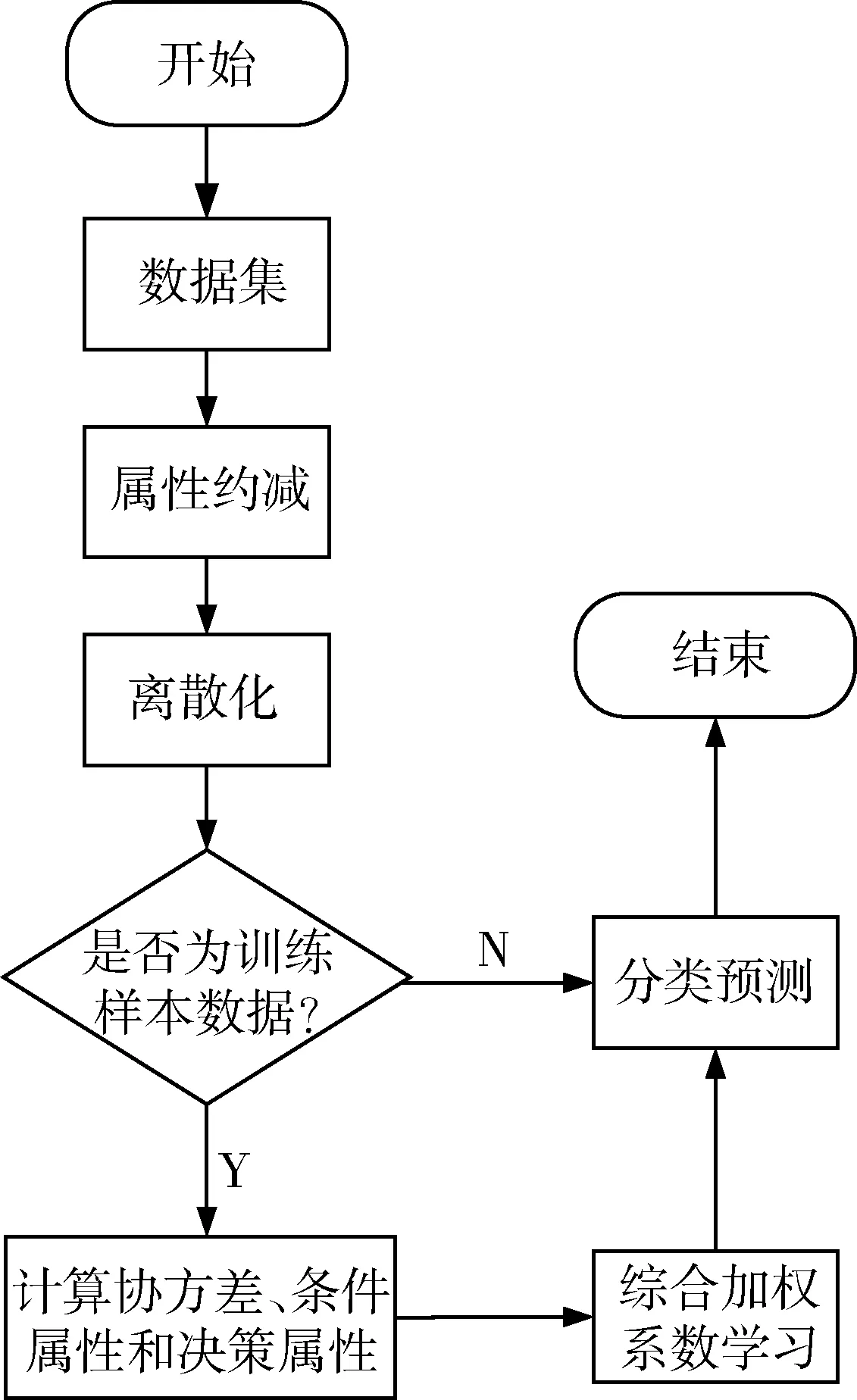
图1 基于CWNBC的入侵检测流程图
该算法的具体步骤如下:
(1)获取原始数据集,对数据集进行预处理,去除冗余属性,对连续数值离散化;
(2)条件判断:若是训练样本数据集,则进行第(3)步,若是需要分类的样本数据则直接进行第(5)步;
(3)统计分析数据集中的条件属性和决策属性。计算在决策属性下其他的条件属性的概率P(Y|X),进而计算Cov(X,Y)、D(X)、D(Y),然后计算出
(4)统计数据集中每个属性取值的个数以及每个值属于某类的样本数,然后做如下计算:
(5)根据上面的计算结果,计算出改进的综合加权系数:
(6)利用朴素贝叶斯分类器进行结构与参数学习,获得改进的综合加权朴素贝叶斯模型;
(7)用新模型对数据集进行分类,获得分类结果。
4 实验结果及分析
4.1 入侵检测数据集
本文实验数据采用的是KDD’99入侵检测数据集,该训练数据集包含7周的网络流量,有5 000 000条连接记录;测试训练集包含2周的网络流量,有2 000 000条连接记录。该研究共模拟了 5大类网络攻击[17-18]。
4.2 结果与分析
为了验证本文提出的算法的准确性和高效性,进行了以下实验测试与分析。为了保证执行的效率,随机选取20 000条记录用于本次实验,并把20 000条连接记录随机分为5组,每组数据的30%作为训练数据,70%作为测试数据。 实验过程中搭建的环境平台所使用的操作系统为Windows8,处理器为Inteli5,CPU频率为1.9GHz,内存为4GB,软件工具为Weka。
在实验中,通过Weka软件自带的工具对连续属性进行离散化和属性约简,得到最终的条件属性有:(1)service;(2)flag;(3)src-bytes;(4)dst-bytes;(5)dst-host-srv-count;(6)diff-srv-rate。
应用多种分类算法进行实验,实验结果如表1所示。

表1 准确率比较表 (%)
本实验将改进的朴素贝叶斯分类算法与其他分类算法在入侵检测方面做了比较,从表1可以看出,本文提出的基于改进朴素贝叶斯的分类算法相对于其他的分类算法在分类准确率上有所提高,证明了本文提出的算法是有效可行的。
5 结束语
本文借鉴前人的一些经验和方法,针对不足之处做了适当的改进,提出了一种基于综合加权系数的朴素贝叶斯分类算法。该算法弥补了朴素贝叶斯分类算法假设属性独立的不足之处,既考虑了属性值的频数与分类的关系,又考虑了属性值的内容对分类的影响。最后经过实验证明,本文提出的算法与其他分类算法相比,有效地提高了分类准确率。但是,本算法仍然有待提高,加权系数仍然有待完善。下一步将继续研究如何优化加权系数,进一步提高分类的准确率,以便适应于更复杂多变的网络数据。
[1] GOVINDARAJAN M,CHANDRASEKARAN R M.Intrusion detection using neural based hybrid classification methods[J].Computer Networks,2011,55(8):1662-1671.
[2] GARCIA-TEODORO P,DIAZ-VERDEJO J,MACIA-FERNANDEZ G,et al.Anomaly-based network intrusion detection:techniques,systems and challenges[J].Computers & Security,2009,28(1/2):18-28.
[3] MOHAMMAD M N,SULAIMAN N.MUHSIN O A.A novel intrusion detection system by using intelligent data mining in weka environment [J].Procedia Computer Science,2011,3(1):1237-1242.
[4] GUINDE N B,ZIAVRAS S G.Efficient hardware support for pattern matching in network intrusion detection [J].Computers & Security,2010,29(7):756-769.
[5] BHUYAN M H.BHATTACHARYYA D K,KALITA J K.Survey on incremental approaches for network anomaly detection[J].International Journal of Communication Networks and Information Security,2011,3(3):226-239.
[6] PANDA M.ABRAHAM A.PATRA M R.A dHybri intelligent approach for network intrusion [J].Procedia Engineering,2012,30(1):1-9.
[7] 杨杰,陈昕,万剑雄.网络协议分析与决策树挖掘的入侵检测模型研究[J]计算机应用与软件,2010,27(2):19-55.
[8] 徐永华,李广水.基于距离加权模版约减和属性信息熵的增量SVM入侵检测算法[J].计算机科学,2012,39(12):76-86.
[9] Li Liu,Zhang Guoyin,Nie Jinyuan,et al.The application of genetic algorithm to intrusion detection in MP2P network[J].Lecture Notes in Computer Science,2012,31(3):390-397.
[10] Wang Gang,Hao Jinxing,Ma Jian.A new approach to intrusion detection using aritificial neural networks and fuzzy clustering[J].Expert Systems with Applications,2010,37(9):6225-6232.
[11] 王行甫,杜婷.基于属性选择的改进加权朴素贝叶斯分类算法[J].计算机系统应用,2015,24(8):149-154.
[12] FRIDEMAN N, GEIGER D,GOLDSZMIDT M. Bayesian network classifiers[J]. Machine Learning, 1997,29(2-3):131-163.
[13] LANGLEY P,IBA W, THOMPSON K. An analysis of Bayesian classifiers[C]. In Proc. of the 10th National Conf. on Artificial Intelligence. Menlo Park: AAAI Press, 1992:223-228.
[14] ZHANG H,SHENG S.Learning weighted naive Bayes with accurate ranking[C].2004 Fourth IEEE International Conference on Data Mining(ICDM’04).IEEE,2004:567-570.
[15] 张步良.基于分类概率加权的朴素贝叶斯分类方法[J].重庆理工大学学报(自然科学版),2012,26(7):81-83.
[16] LIN J, YU J. Weighted naivebayes classification algorithm based on particle swarm optimization[C].2011 IEEE 3rd International Conference on Communication Software and Networks (ICCSN). IEEE,2011:444-447.
[17] STOLFO S J,LEE W,CHAN P K,et al.Dataming-based intrusion detectors:an overview of the Columbia IDS project[J].ACM SIGMOD Record,2011,30(4):5-14.
[18] 史美林,钱俊,许超.入侵检测系统数据集评测研究[J].计算机科学,2006,33(8):1-8.
Intrusion detection methods based on improved Naive Bayesian
Sun Cheng,Xing Jianchun, Yang Qiliang, Han Deshuai
(College of Defense Engineering, PLA University of Science and Technology, Nanjing 210007,China)
The network security of industry control system is becoming a significant issue as the intrusions are becoming more complicated and diversified. Due to increasing complexity and openness, it is exposed to more intrusions and becoming more vulnerable than ever.In order to resist diverse intrusions,more efficient intrusion detection methods need to be designed. Naive Bays classification algorithm is a sample and effective classification algorithm, which adapts to intrusion detection of industry control system network, but its attribute independence hypotheses makes it incapable to express the dependence among attributes, and affects its classification performance. Concerning this problem, we put forward an improved compositive weighted Naive Bayes classification algorithm based on the experience of the predecessors. The algorithm not only considers the effect on classification by the different attribute value, but also considers the effect on classification by the content of attribute value, and introduces the compositive weighted coefficient skillfully. Then we make a comparison between this algorithm and other algorithms. The result shows that the proposed algorithm has higher classification accuracy than other algorithms. And it can be beter applicable to the intrusion detection of complex industrial control system network.
Naive Bays;weighted coefficient;attribute value
江苏省自然科学基金(BK20151451)
TP31
A
10.19358/j.issn.1674- 7720.2017.01.003
孙程,邢建春,杨启亮,等. 基于改进朴素贝叶斯的入侵检测方法[J].微型机与应用,2017,36(1):8-10,14.
2016-09-08)
孙程(1990-),男,硕士生,CCF会员,主要研究方向:软件安全。
邢建春(1964-),通信作者,男,博士,教授,CCF高级会员,主要研究方向:复杂智能信息系统、信息物理融合系统。E-mail:820808595@qq.com。
杨启亮(1975-),男,博士,副教授,CCF高级会员,主要研究方向:自适应软件、信息物理融合系统。

