多绕组变压器具有辐射形等值电路的充分必要条件
朱永强, 郝嘉诚
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
多绕组变压器具有辐射形等值电路的充分必要条件
朱永强, 郝嘉诚
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
多绕组变压器被广泛应用于电力系统中,但其等值电路往往比较复杂,参数计算难度大,并且难以实现对变压器各绕组的独立控制,在实际应用中给主电路的分析与控制器的设计增加了难度。而辐射形等值电路模型结构清晰简单,便于分析和控制,因此有必要探究多绕组变压器具有辐射形等值电路的条件。将多绕组变压器每一绕组的自感系数和互感系数作为基本参数,从各绕组的正弦稳态电压平衡方程出发,忽略励磁电流的影响,推导出多绕组变压器具有辐射形等值电路的充分必要条件,并以变压器的常用参数——短路阻抗的形式表示。
多绕组变压器; 等值电路; 短路阻抗
0 引 言
多绕组变压器在电力系统中的应用非常广泛,如用于大容量不平衡负荷补偿的变压器隔离型结构的同步补偿器[1];用于调节电压、补偿无功的多绕组变压器型可调电抗器[2];适用于高压大容量场合的高频多绕组变压器多电平变换器[3]等。这些应用了多绕组变压器的电力设备与其他同类设备相比,都具有其独特的优越性。但是,由于多绕组变压器各绕组共用铁心,彼此之间存在电磁耦合关系,等效电路中会存在受控源[4]。当低压绕组数目越多时,含受控源的等效电路就会越复杂[5],这就导致多绕组变压器无法像三绕组变压器那样在任何情况下都具有辐射形等值电路,这也使得其在应用时的主电路分析及控制电路的设计变得更为复杂,给工程实际应用和参数计算增加了难度。等值电路模型是分析变压器的有效工具。所以,在一定假设条件下,研究一个较为简单实用的多绕组变压器的等值电路模型具有很重要的意义。
目前,针对多绕组变压器等值电路模型进行研究的文献并不多。其中,文献[6-7]将各绕组之间的耦合数目与多边形自身特点相结合,并假设变压器阻抗矩阵非奇异,给出了多绕组变压器的多边形等值电路模型;文献[7-8]针对同心式多绕组变压器,在假设各绕组电抗高度和径向厚度相同的条件下,建立了梯形等值电路模型;上述两种模型均在推导过程中做了特定假设,且推导过程复杂。文献[9-10]提出了(n-1)射线形等值电路模型,但它忽略了变压器各副边绕组之间的电磁耦合作用;文献[11]从多绕组变压器的基本电压方程入手,通过一系列公式变换,给出了多绕组变压器等效成辐射形等值电路的充分必要条件,但其仅指出了各绕组之间互感系数所必须满足的条件,与变压器的实际参数难以形成对应关系,不便于指导工程实践。
本文在忽略励磁电流的前提条件下,对多绕组变压器的基本电压方程进行相应变换,推导出多绕组变压器具有辐射形等值电路的充分必要条件,并给出了辐射形等值电路模型。
1 多绕组变压器的基本电路方程
单相多绕组变压器的结构示意图,如图1所示。当变压器的绕组个数大于2时,由于共用铁心,各个绕组在磁路方面互相耦合,所以在建立电压方程时,不能再简单套用双绕组变压器中主磁通和漏磁通的概念进行分析,需要使用每一绕组的自感系数和各绕组之间的互感系数作为基本参数来列写电压方程[12]。
当不考虑铁心损耗时,按照图1所标注的电压和电流方向定义变压器各绕组电压和电流的正方向,则各绕组的正弦稳态电压平衡方程为
(1)
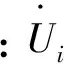
由于变压器原边绕组和副边绕组的电压等级不同,所以按照式(2)将副边绕组的各电气量折算至原边绕组。假设变压器绕组1为原边绕组,其余绕组均为副边绕组,则有
(2)
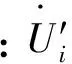
依式(2)将副边绕组各电气量折算至原边绕组后,各绕组正弦稳态电压平衡方程为
(3)
为书写方便,在下文中所有的折算量均用不带撇的符号表示。
2 多绕组变压器的一般等效电路
2.1 三绕组变压器
原边绕组(绕组1)和绕组2间的电压降为
(4)
同理,原边绕组(绕组1)和绕组3间的电压降为
(5)
同理,绕组2和绕组3间的电压降为
(6)
根据式(2)、式(4)、式(5)和式(6),三绕组变压器的等值电路可以用如图2所示的形式表示。在该种形式下对变压器绕组参数的对称性没有要求。
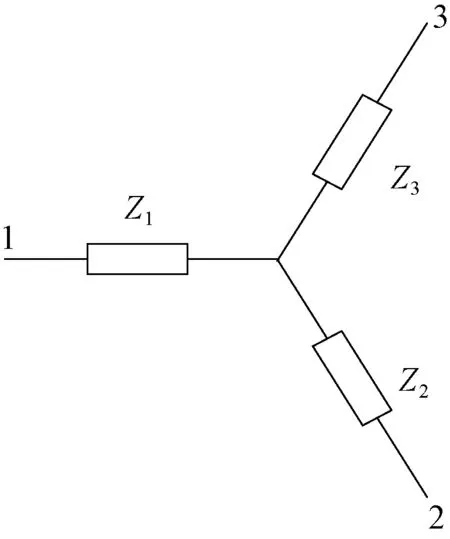
图2 三绕组变压器等值电路模型Fig.2 The equivalent circuit model of three-winding transformer
其中,
(7)
2.2 多绕组变压器
但是,当变压器绕组数多于三个时,情况要复杂得多。多绕组变压器并不能在任何情况下都像三绕组变压器那样具有如图2所示的辐射形等值电路。文献[11]和文献[13]给出了四绕组变压器和六绕组变压器一般形式的等值电路,分别如图3(a)、(b)所示。
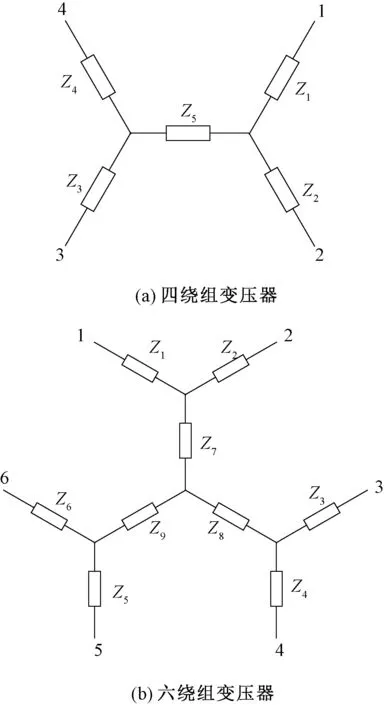
图3 多绕组变压器等值电路模型Fig.3 The equivalent circuit model of multi-winding transformer

图4 多绕组变压器多边形等值电路模型Fig.4 The polygon type equivalent circuit model of multi-winding transformer
在忽略励磁电流的条件下,n绕组变压器短路阻抗数等于绕组之间的耦合数目n(n-1)/2,而n边形两两顶点之间的连线数恰好等于n(n-1)/2,文献[6,7]利用这一特点,给出了四绕组变压器和六绕组变压器的多边形等值电路模型,分别如图4(a)、(b)所示。
从图3和图4可以明显的看出,不论是一般形式的等值电路还是多边形的等值电路,多绕组变压器的等值电路都非常复杂。并且不论在哪种形式的等值电路下都无法实现对变压器各绕组的独立控制。由于不能忽略各绕组之间的电磁耦合关系,多绕组变压器便不能像三绕组变压器那样在任何情况下都具有如图2所示的辐射形等值电路。
由于辐射形等值电路结构简单清晰,易于主电路的分析和控制器的设计。因此,下文将要探究的问题是:能否在一定的合理假设条件下,使得多绕组变压器具有简单且易于分析的辐射形等值电路。
3 多绕组变压器等效为辐射形等值电路模型的充分必要条件
3.1 三绕组变压器
当n=3,即变压器为三绕组变压器时,根据式(4),将原边绕组(绕组1)和绕组2间的电压降公式变换为
(8)
根据式(5),将原边绕组(绕组1)和绕组2间的电压降公式变换为
(9)
同理,根据式(6),将绕组2和绕组3间的电压降公式变换为
(10)
其中,
(11)
上述这些阻抗叫做三绕组变压器的等值阻抗。显而易见,Z123=Z132,Z213=Z231,Z312=Z321。
通过式(8)~(10)可以看出,对于三绕组变压器,任意两绕组间的电压降等式具有相类似的形式,即电压降仅与流过该绕组的电流有关,且这几式中各个绕组电流的系数均相等。根据以上结果,令Z1=Z123=Z132,Z2=Z213=Z231,Z3=Z312=Z321,即可以得到如图5所示的三绕组变压器辐射形等效电路。
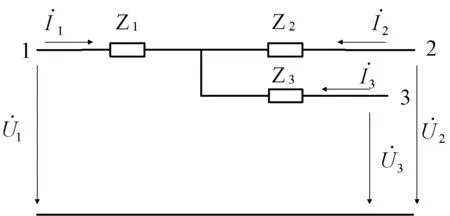
图5 三绕组变压器辐射形等值电路模型Fig.5 The radiant equivalent circuit model of three-winding transformer
三绕组变压器等值电路中的参数可以用变压器短路试验来确定。在进行任意两绕组之间的短路试验时,第三个绕组开路。此时,三绕组变压器的运行状态相当于双绕组变压器。因此,图5中任意两端子之间的阻抗等于相应两绕组之间的短路阻抗,则有
(12)
解上述方程组,得
(13)
图5本质上与图2相同,但是上述文章中对于等值阻抗的定义为探寻多绕组变压器具有辐射形等值电路的条件提供了思路。
3.2 多绕组变压器
当n>3时,多绕组变压器第k个绕组和第m个绕组之间的电压降为
(14)
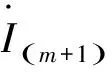
(15)
其中,等值阻抗
(16)
式中:Zk-m为变压器绕组k与绕组m之间的短路阻抗(k=1,2,…,n,m=1,2,…,n,且k≠m),则有
Zk-m=rk-m+jxk-m
(17)
rk-m=rk+rm
(18)
(19)
由式(14)~(17)可得
(20)
显而易见,Zkmn=Zknm。
从以上推导可以看出,如果多绕组变压器任意两绕组之间的短路阻抗已知,则可以根据式(16)算出相应的等值阻抗Zkmn的大小。变压器各绕组间的短路阻抗可以通过短路实验和计算得到。
当变压器绕组数目n>3时,多绕组变压器具有辐射形等值电路的充分必要条件是:多绕组变压器任意两绕组之间的电压差,都能表示成其电流与确定阻抗的乘积之差。即需同时满足:
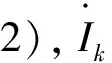
(2) 第k个绕组与第m个绕组之间的电压降,仅与流过这两个绕组的电流有关,与流过其他绕组的电流无关,即要求式(15)中的第三项
(21)
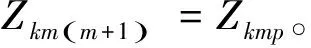
综合上述两个条件,多绕组变压器具有辐射性等值电路的充分必要条件可以总结为:多绕组变压器每一个绕组的等效阻抗均为某一确定的常数,即任一绕组k的等效阻抗Zkxy=Ck。其中,Ck为某一确定的常数,k=1,2,…,n,x=1,2,…,n,y=1,2,…,n,且x≠y,x≠k,y≠k。需要说明的是,当k取不同的值时,Ck的值不一定相同。
下面证明上述条件的充分必要性。
(1) 证明充分性。
当多绕组变压器任一绕组k的等效阻抗Zkxy=Ck,其中,Ck为某一确定的常数,k=1,2,…,n,x=1,2,…,n,y=1,2,…,n,且x≠y,x≠k,y≠k。根据式(15),有
(22)
从上式可以得出,当多绕组变压器每一绕组的等效阻抗都为某一确定的常数时,任意两个绕组的电压差都能表示成其电流与确定阻抗的乘积之差。所以,在该种条件下,多绕组变压器具有辐射形等值电路,充分性得证。
(2) 证明必要性。
若多绕组变压器具有辐射形等值电路,则对于绕组k和绕组m,其中k=1,2,…,n-1,m=2,3,…,n且m>k,有
(23)
式中:Zk和Zm分别为绕组k和绕组m的等效阻抗,且Zk和Zm均为某一确定的值。
又
(24)
联立求解式(23)和式(24),可得
(25)
(26)
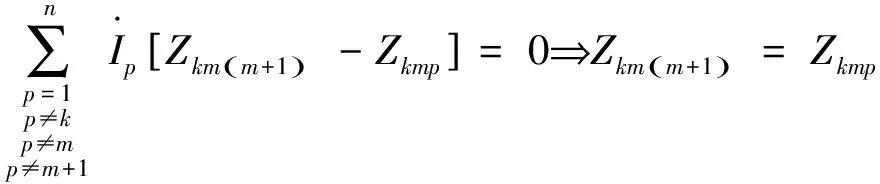
(27)
综合式(25)~(27),当多绕组变压器具有辐射形等值电路的时候,对于多绕组变压器的任一绕组k,其等效阻抗Zkxy为一确定的值,其中,k=1,2,…,n,x=1,2,…,n,y=1,2,…,n,且x≠y,x≠k,y≠k,必要性得证。
证毕。
基于前文所推导出的多绕组变压器具有辐射形等值电路的充分必要条件,为简便起见,令Zk=Zkxy,k=1,2,…,n。多绕组变压器辐射形等值电路如图6所示。
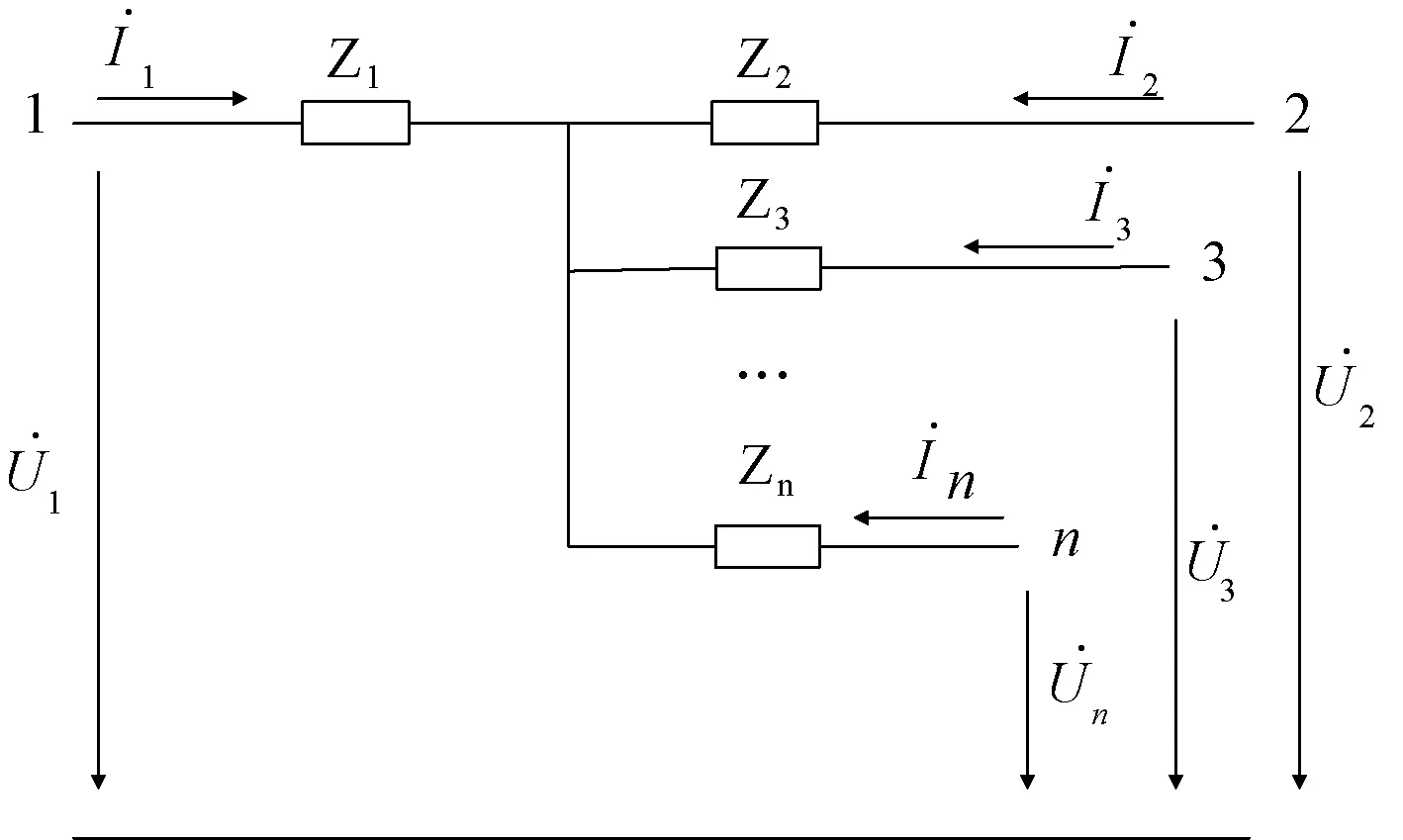
图6 多绕组变压器辐射形等值电路模型Fig.6 The radiant equivalent circuit model of multi-winding transformer
4 结 论
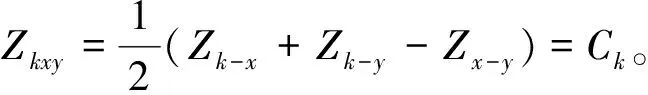
多绕组变压器在电力系统中的应用非常广泛,如变压器隔离型STATCOM、变压器式可控电抗器、多绕组变压器型变换器等。辐射形等值电路模型结构清晰简单,便于分析,可以实现对多绕组变压器各绕组的独立控制。辐射形等值电路的参数及等效条件均由变压器实际参数——短路阻抗表示,有助于指导满足等效条件的多绕组变压器的设计和制造,有利于应用了多绕组变压器的电磁装置的分析和设计,同时也有利于构建满足等效条件的多绕组变压器的仿真模型。
[1] 朱永强,宋强,刘文华,等. 用于不平衡负荷补偿的大容量D-STATCOM主电路选择[J]. 电力系统自动化,2005,29(7):58-64.
[2] 田军,陈乔夫,张宇. 基于双端口网络控制的多绕组变压器型可调电抗器[J]. 电工技术学报,2010,(2):60-66.
[3] 顾春阳,李永东,郑泽东,等. 多绕组高频变压器隔离式多电平变换器研究[J]. 电工技术学报,2014,(8):97-102.
[4] NIEMELA V A,OWEN H A, WILSON T G. Cross-coupled-secondaries model for multiwinding transformers with parameter values calculated from short-circuit impedances[C]. IEEE Annual Power Electronics Specialists Conference,San Antonio,TX,USA,1990: 822-830.
[5] 许加柱,梁湘湘,姚新丽,等. 基于等效单匝电感矩阵的多绕组变压器复合短路阻抗及环流计算[J]. 中国电机工程学报,2011,31(34):135-141.
[6] C.B.瓦修京斯基.变压器的理论与计算[M].北京:机械工业出版社,1983.
[7] 田铭兴,励庆孚.多绕组变压器的多边形等值电路模型[J].西安交通大学学报,2004,38(6):636-640.
[8] WANG J, WITULSKI A F,VOLLIN J L,et al. Derivation, calculation and measurement of parameters for a multi-winding transformer electrical model[C]. Proceedings of APEC ′99 - Applied Power Electronics Conference,1991,1(11):220-226.
[9] Александров Г Н. Принципы работы управляемо го шунтирюще го реактора трансформаторно го типа[J]. Электротехника,1995,66(11):30-34.
[10] SUN Chiping,KUTKUT N H,NOVOTNY D W,et al. General equivalent circuit of a multi-winding co-axial winding transformer[C]. IEEE IAS Meeting,Orlando,USA,1995,3:2507-2514.
[11] ZHU Yongqiang,HAN Minxiao,YIN Zhongdong. Sufficient conditions and error analysis on radial equivalent circuit of multi-winding isolating transformers used in power electronic devices[C]. Proceedings of APCCAS 2008 - 2008 IEEE Asia Pacific Conference on Circuits and Systems,November 30 - December 3,2008,Macao,China:1838-1840.
[12] 罗隆福,张志文,邓建国,等.多绕组变压器复合短路阻抗的求解方法[J].电工技术学报,2002,17(3):39-42.
[13] 刘淑华.变压器和互感器的电路计算与相量变换[M].北京:水利电力出版社,1978.
The Necessary and Sufficient Conditions of Multi-winding Transformer Generating Radiant Equivalent Circuit
ZHU Yongqiang,HAO Jiacheng
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University,Beijing 102206,China)
Multi-winding transformer is widely used in power system. But the equivalent circuit model of multi-winding transformer is always complicated, and its parameter is difficult to compute. It is hard to take independent control of each winding. All above factors make it hard to analyze the main circuit of the system and design the controller. The structure of radiant equivalent circuit model is clear and simple, which makes it easy to analyze and control. So it is necessary to study the conditions in which the multi-winding transformer generates radiant equivalent circuit. Based on the concept of mutual inductance coefficient and self-inductance coefficient, this paper gives the sinusoidal steady-state voltage balance equation of each winding. The radiant equivalent circuit model of multi-winding transformer is derived from the voltage equations by ignoring the effects of exciting current. Finally, this paper presents the necessary and sufficient conditions of radiant equivalent circuit with short-circuit impedance.
multi-winding transformer;equivalent circuit;short-circuit impedance
2016-03-11.
国家高技术研究发展计划(863计划)资助项目(2015AA050102).
10.3969/j.ISSN.1007-2691.2016.06.03
TM426
A
1007-2691(2016)06-0013-07
朱永强(1975-),男,副教授,研究方向为电力电子技术、新能源电力变换技术等;郝嘉诚(1992-),女,硕士研究生, 研究方向为电力电子与电力传动。

